Introduction

A report from the European Commission shows that there has been an increase in the number of circus companies and workers in this sector between 2003 and 2020, providing the figure of around 1,600–2,100 registered circus companies in 2020 in the European Union.¹ More locally, En Piste, an organization that brings together circus arts professionals and organizations in Canada, counts nearly 100 circus enterprises (companies, schools, social circus organizations and event diffusers) in Quebec² in 2020.

Circus injury patterns and rates have been investigated among professional artists,^3–6 student artists^7–9 and adolescents.¹⁰ Several longitudinal studies focused on the Cirque du Soleil company,⁴ National Institute of Circus Arts in Australia,⁷ National Center for Circus Arts in France⁸ and the Montréal Circus School.⁹ Although definitions of injury are inconsistent, equipment is mentioned as an external factor of injury.^6,8,11

The safety of acrobats is a major concern in the circus community as circus practice involves design and rigging of equipment that must withstand high loads.^11,12 For example, the theme of this year’s conference at the European Federation of Professional Circus Schools (FEDEC), a federation of 41 European and international professional circus schools, was “safety” to answer the needs of riggers in professional circus schools.¹³ Understanding the forces acrobats are likely to exert on the circus and rigging equipment is an essential factor to ensure their safety. The American ANSI E1.43:2016 safety standard for entertainment technology provides guidance for the design, manufacture, use and maintenance of performer flying systems.¹⁴ While the standard is used for rigging, it explicitly excludes “any connection that ultimately relies on the strength or ability of the Flying Performer,” ¹⁴ which is the case for most circus equipment. For example, the standard sets minimum design factors related to the working load limit (WLL), the characteristic load and the peak load for rigging. The WLL is described as “the maximum weight as defined by the Flying System Designer that a User is allowed to apply to a lifting medium in the performer flying system.” ¹⁴ The characteristic load and the peak load are the maximum forces applied to the system resulting from normal use and abnormal use, respectively. However, with no data available on the characteristic load or the peak load, it is not possible for circus professionals to compute the proper target. Furthermore, rigging hardware used in circus could be sourced from many industries, including entertainment, climbing or industrial rigging. If equipment intended for one of these activities is to be repurposed for circus practice, it is crucial that the circus professional confirms that rigging will meet the specific mechanical demands to ensure the safety of the circus performer.

New circus equipment is frequently created, and professionals sometimes use a “dynamic factor” to estimate the actual force applied by the performer to safely design new equipment. There are no standard values for the dynamic factor, resulting in it falling in a range of 3–10 depending on the practice.^15,16 In rigging, a design factor is applied between the dynamic force (static force × dynamic factor) or directly the static force and the maximum strength of the equipment.^17–19 Other terms frequently used for the design factor are “safety factor” or “factor of safety.”^20,21 In engineering design, a safety factor is applied to the dynamic force while designing a piece of equipment. It expresses how much more force the designed part will actually be able to withstand compared to the dynamic force.²²

To ensure that the rigging and circus equipment are strong enough to withstand the acrobatics, riggers and circus designers need knowledge about the actual forces that are applied to the equipment. Very few studies have investigated forces applied by circus acrobats on their equipment. In a previous study, we measured dynamic forces at the rigging points of five aerial circus apparatuses.¹⁵ These results led to safety and design recommendations to enhance circus practice and optimize circus equipment. However, circus disciplines are extremely diverse and not limited to these five aerial apparatuses, so more data is still needed. While disciplines such as rings in gymnastics,²³ slackline²⁴ and vertical jumps with acrobats²⁵ have been covered in the literature, a multitude of other disciplines in circus still need to be investigated. Therefore, the aims of the present study were (1) to assess maximal forces generated by circus acrobats for various acrobatic figures on nine circus disciplines, that is, aerial hoop, rope, aerial silk, flying pole, tightwire, Chinese pole, swinging trapeze as well as solo and duo fixed trapeze, and (2) to evaluate the differences of maximal force between participants.

Methods

Thirty-four acrobats (19 females and 15 males; age: 27.1 ± 7.3 years; height: 1.71 ± 0.10 m; body mass: 61.5 ± 9.2 kg, including 23 professionals, with years of experience: 9.1 ± 4.5 years, and 11 students from professional circus schools) from nine circus disciplines gave their written informed consent to participate in this study. The project was approved by both the ethical research committees of Polytechnique Montréal and of the National Circus School of Montréal. The number of acrobats by discipline were as follows: five in aerial hoop, five in rope, two in silk, two in flying pole, four in tightwire, five in Chinese pole, four in (solo) swinging trapeze, three in solo fixed trapeze and two duos (4 acrobats) in duo fixed trapeze.

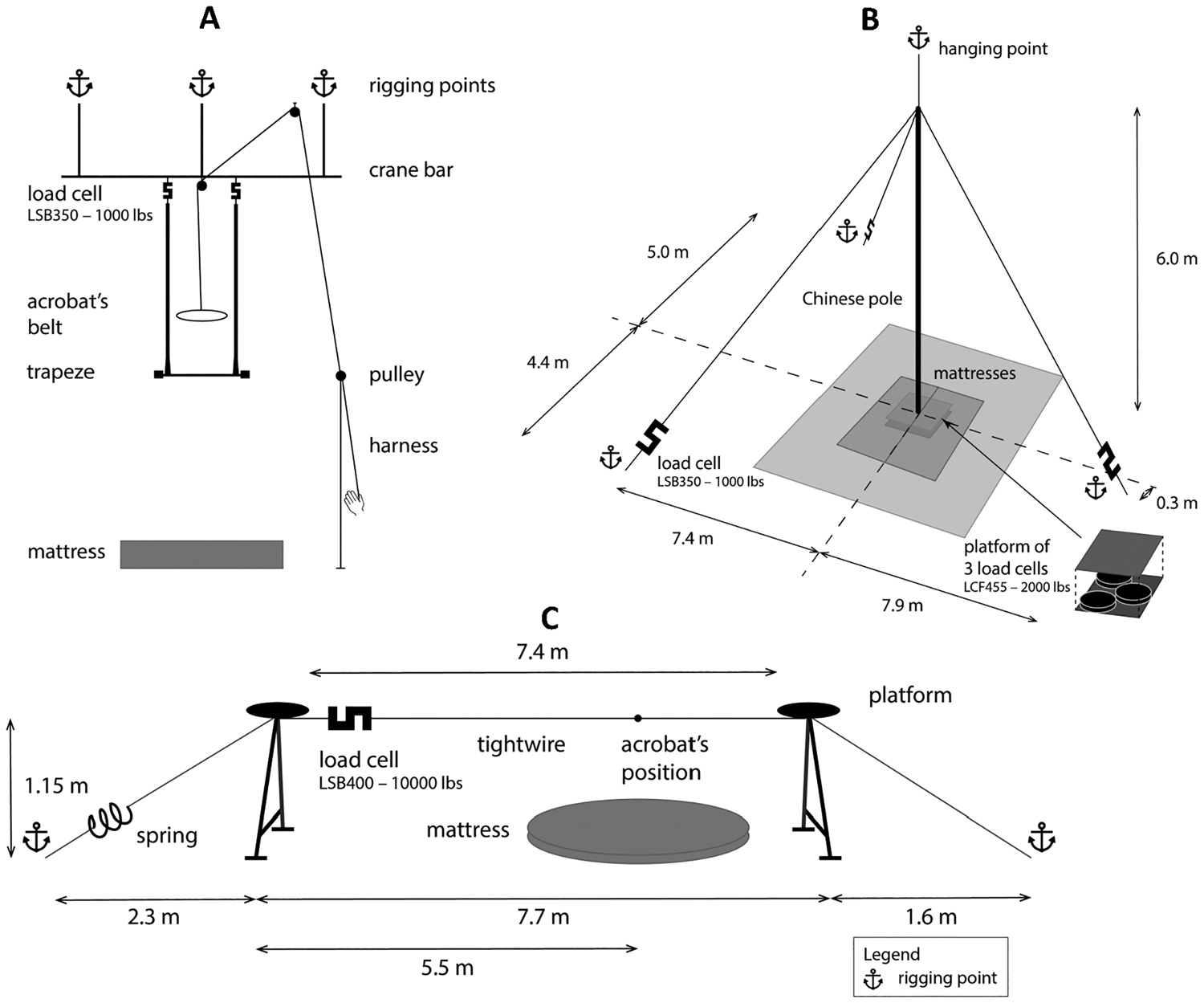
The tests took place at the National Circus School of Montréal. Circus equipment are detailed in Appendix 1. Specific dimension and location of load cells are presented in Figure 1. Three different types of load cells (LSB350–1,000 pounds (lbs), LCF455–2,000 lbs and LSB400–10,000 lbs; Futek, Irvine, US) were placed at the rigging points of the circus apparatus (Figure 1) and connected to one data acquisition chassis (cDAQ-9184 and cDAQ-9191; National Instruments, Austin, Texas, US). A VPN router (DSR-250; D-Link, Canada) linked the load cells and the Basler IP camera (Basler BIP2–1920c; National Instruments, Austin, Texas, US) to the computer (G750JS; Asus). The force data and the video files were saved on the computer with the help of a LabVIEW 2015 program (LabVIEW software; National Instruments). The sample rate of 2,000 hertz (Hz) was used for all load cells. A wide shot of the acrobat was recorded by a second camera on a tripod. The setup for single-point aerial disciplines (aerial hoop, rope, aerial silk and flying pole) was similar to our previous study,¹⁵ except that the emitter was replaced by a cDAQ-9191 Wi-Fi chassis connected to the router. Load calibration certificates provided by the supplier indicated the sensitivity value for all eight load cells (4 LCF455, 3 LSB350 and 1 LSB400). Before the test with participants, adjusted values of load cell sensitivity were obtained by a manual calibration using two calibrated masses of 45.4 kg and additional weightlifting disks, previously weighted, for a maximum mass of 295.6 kg.

Figure 1. Setup for (A) trapeze; (B) Chinese pole and (C) tightwire.

All measurements for a given discipline were carried out under the same experimental conditions including equipment, rigging point and starting height (in aerial rope or aerial silk). Before data collection, each participant warmed up with their own regular routine exercises for a duration of 10 to 20 minutes. Acrobats performed four figures that were repeated four to six times. The figures were selected beforehand by coaches from the circus school with two instructions: the figures selected should be considered classic or standard, which are perceived as generating high loads. However, even though standard figures were selected, circus acrobats aimed for a unique performance, and the result was a non-standardized technique. Consequently, some figures could not be performed by all acrobats from the same discipline. Additional acrobatic figures chosen by the acrobats were also recorded once or twice to test figures they considered to generate high loads. Participants could take as much rest time as needed between each figure. The participants wore their regular clothes or accessories as required for their disciplines, that is, their regular custom-made shoes with thin and flexible leather insoles in tightwire, long sleeves to avoid burns in Chinese pole and flying pole and gaiters in swinging trapeze. Missed repetitions were not included in the data analyzed. A total of 673 data sets were collected for 118 acrobatic figures.

For the tightwire and the Chinese pole setups, the preload values in cables were included in the measurements. For the other setups, the circus equipment weight was excluded from the force measurements, as the load cells were tared once the setup was completed. A test protocol and a calculation were used to determine an equivalent vertical force expressed in bodyweight (BW) to the tension force in the cable in tightwire (Appendix 2).

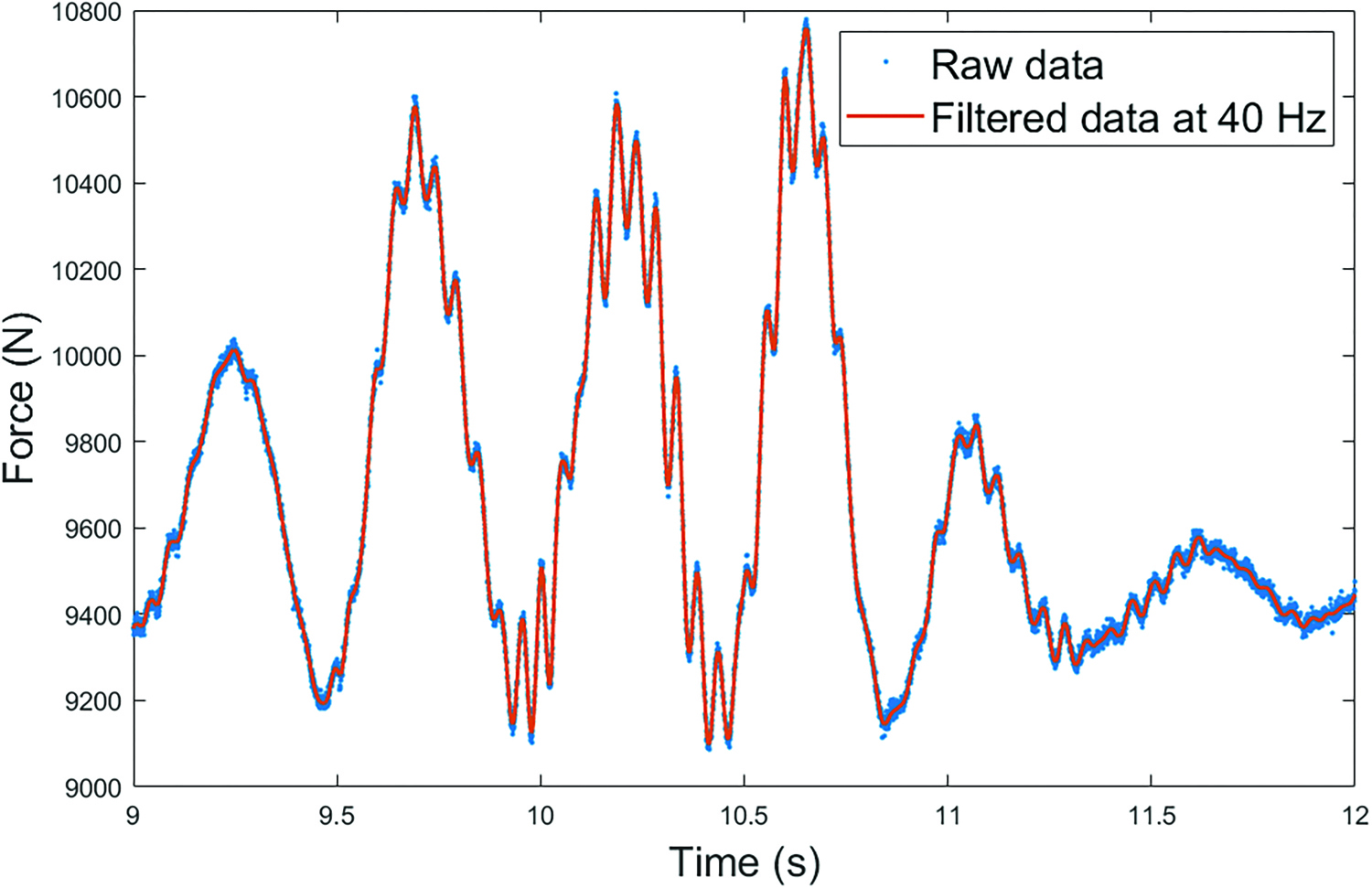
Signal data was smoothed using a fourth-order low-pass Butterworth filter with a cut-off frequency of 40 Hz determined by residual analysis.²⁶ The filtering at 40 Hz did not over-smooth the data and was able to capture all the peaks in the force (Figure 2). Data analysis was done using a MATLAB script (MATLAB R2019a software; The MathWorks Inc., Natick, Massachusetts, US). For the three trapeze disciplines, force data was summed from both cables. For each trial, the maximal force was calculated and expressed in BW from the weight of the acrobat in all disciplines except Chinese pole. In duo fixed trapeze, the force was normalized in BW by the sum of the masses of the two acrobats. The forces in the three cables of the Chinese pole could not be calculated in BW because of the configuration.

Figure 2. Raw and filtered force data for the movement “runs” in tightwire.

In order to assess the differences among participants performing the same movement, one-way analysis of variance (ANOVA) was conducted to compare maximal forces. The statistical analysis was performed for each movement with a minimum of three participants who executed the movement at least four times each. We kept six movements in tightwire, five movements in Chinese pole, three movements in aerial hoop and swinging trapeze and one movement in rope. When differences were detected, the Tukey test was used post hoc to identify specific differences between participants. The significance criterion was subjected to Bonferroni correction as p < 0.05/n, where n is the number of movements by disciplines. For example, significance was set at p < 0.0025 for the Chinese pole discipline because we conducted twenty analyses on this discipline (5 movements × forces in the 3 cables and on the ground = 20). Shapiro–Wilk test was performed to check the normal distribution. All analyses were performed with the software R²⁷ and all graphs with the software MATLAB (MATLAB R2019a software; The MathWorks Inc.).

Results

Differences between participants

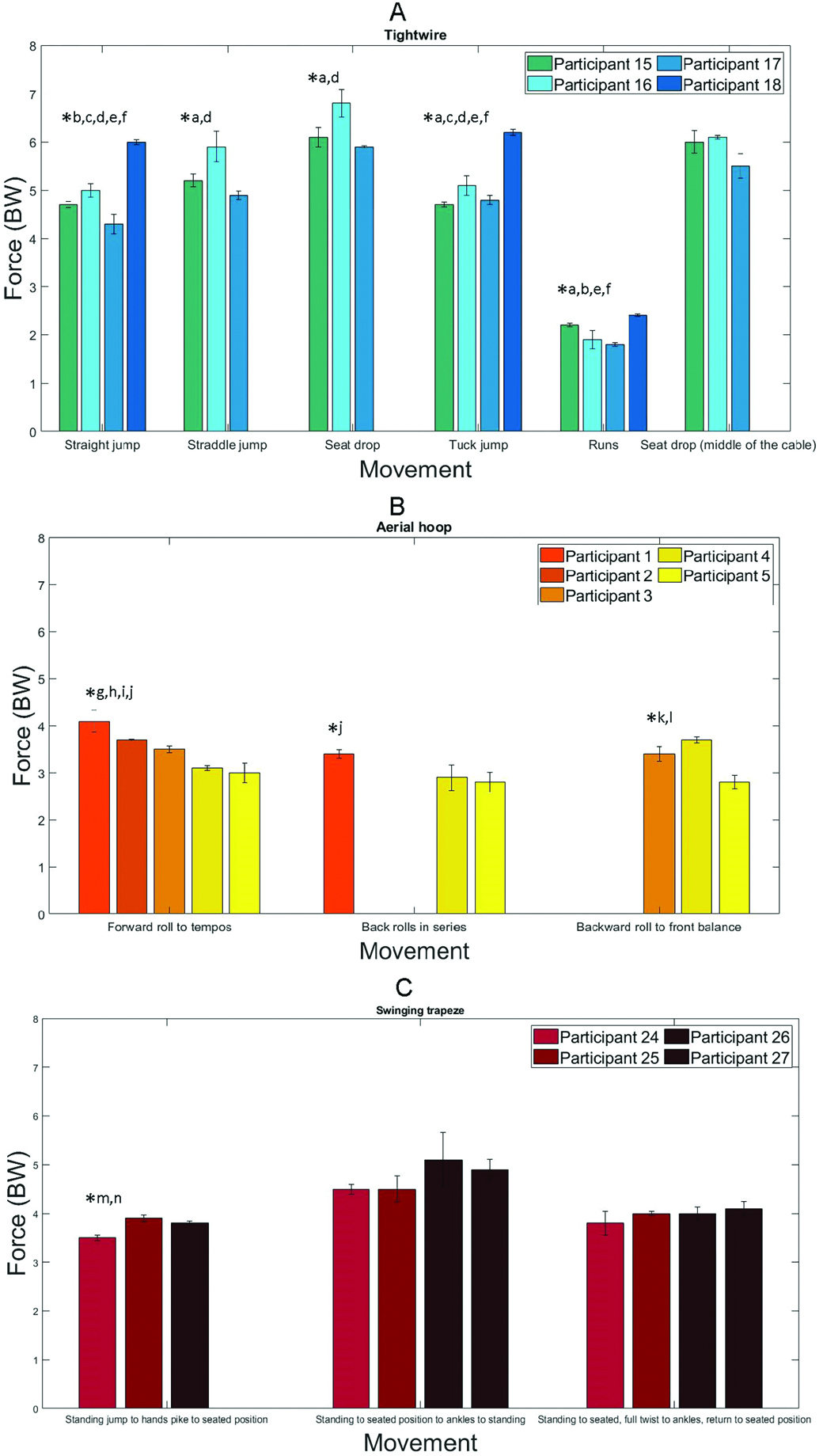
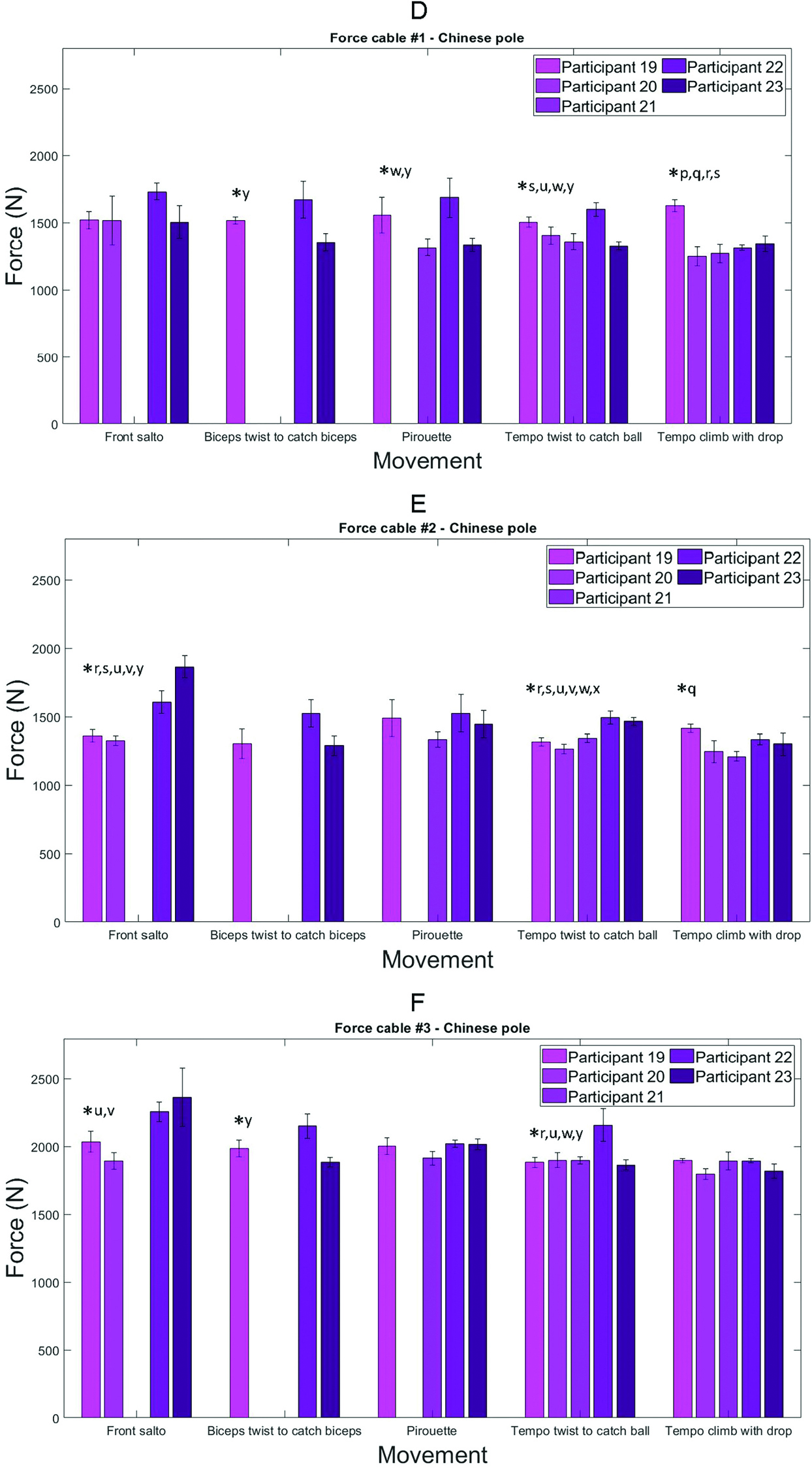
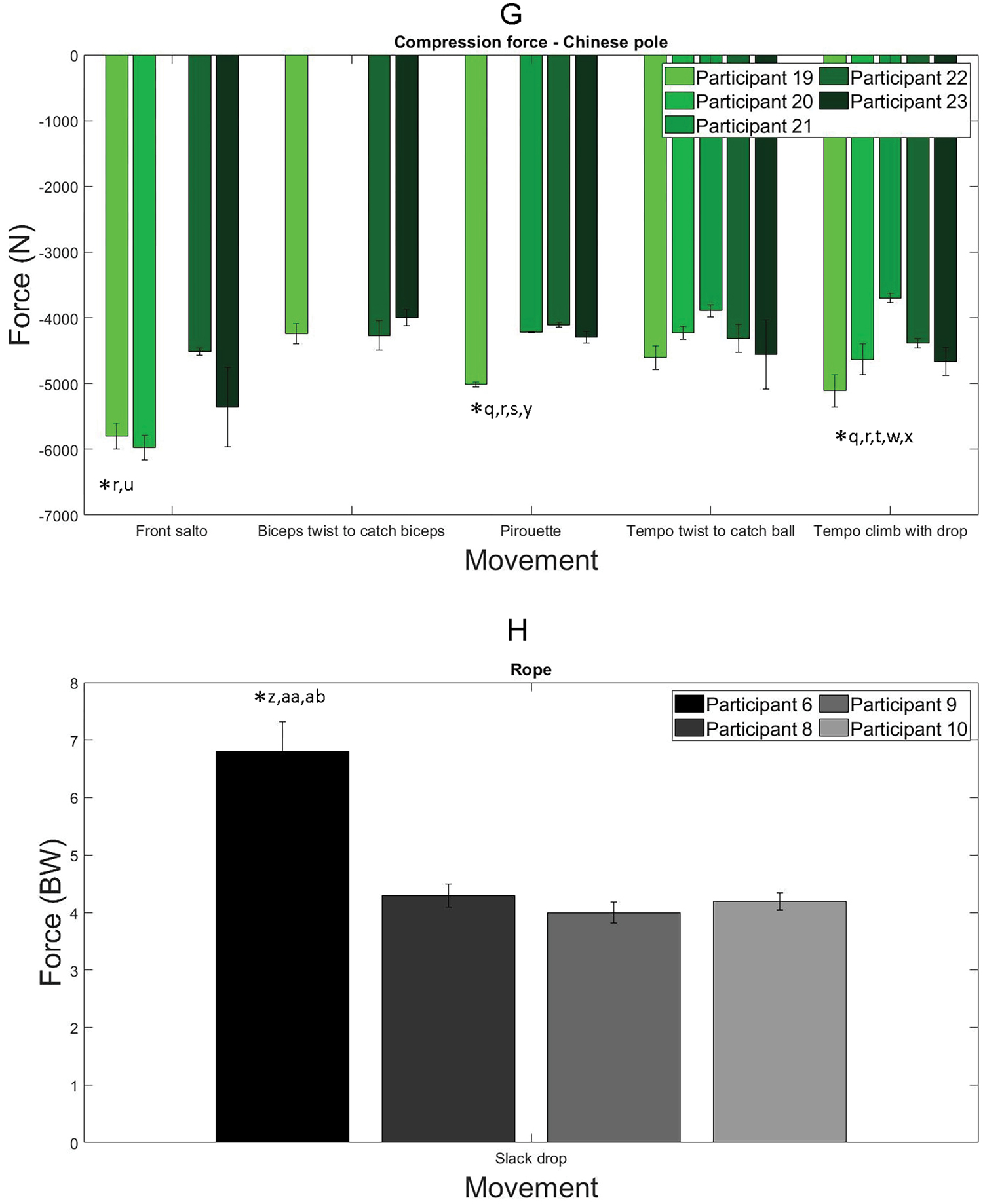
Figure 3 shows the result of the statistical analysis for the six movements in tightwire, five movements in Chinese pole, three movements in aerial hoop and swinging trapeze and one movement in rope selected for the study. Significant differences were found in all disciplines (Figure 3). The descriptions of movements in Figure 3 are presented in Table 2. Except for the slack drop in rope, the pirouette and front salto in Chinese pole, the movements that generated the maximal force presented in Table 1 were performed once by an acrobat or were not performed by enough participants to be included in the statistical analysis.

Figure 3. Mean and standard deviation of maximal force for the movements selected for the statistical analysis in (A) tightwire, (B) aerial hoop, (C) swinging trapeze, (D) Chinese pole—cable #1, (E) Chinese pole—cable #2, (F) Chinese pole—cable #3, (G) Chinese pole—compression force and (H) rope. *Significant difference (p < 0.05/n with n = number of movements per discipline) among movements. Post-hoc comparisons: significant differences (p < 0.05) between participant ^a15 and 16, ^b15 and 17, ^c15 and 18, ^d16 and 17, ^e16 and 18, ^f17 and 18, ^g1 and 2, ^h1 and 3, ⁱ1 and 4, ^j1 and 5, ^k3 and 5, ^l4 and 5, ^m24 and 25, ⁿ24 and 26, ^p19 and 20, ^q19 and 21, ^r19 and 22, ^s19 and 23, ^t20 and 21, ^u20 and 22, ^v20 and 23, ^w21 and 22, ^x21 and 23, ^y22 and 23, ^z6 and 8, ^aa6 and 9 and ^ab6 and 10.

Table 2.

Description of the movements presented in Figure 3.

Movement	Discipline	Description
Straight jump	Tightwire	The artist jumps with straight legs on the wire.
Straddle jump	Tightwire	The artist jumps with legs in a straddle position.
Seat drop	Tightwire	From a standing position, the artist drops to a seated position, rebounds from the seated position and returns to a balanced standing position.
Tuck jump	Tightwire	The artist jumps with legs in a tucked position.
Runs	Tightwire	The artist runs while balancing on the wire.
Forward roll to tempos	Aerial hoop	From a position inside the hoop, the artist places their hands on the lower half of the hoop, performs a forward roll and begins tempos underneath the hoop.
Back rolls in series (from elbows)	Aerial hoop	Placing the hoop behind the back, the artist holds the hoop in their elbows as they use the momentum of their legs to spin around the bottom half of the hoop.
Backward roll to front balance	Aerial hoop	With hands placed on the top of the hoop, the artist begins tempos with the hoop in front of the hips. As the artist is in the front half of the tempo, they perform a backward roll around the bottom half of the hoop to finish in a front balance position.
Standing jump to hands, pike to seated position	Swinging trapeze	The artist drops from a standing position to a position hanging from the arms on the front tempo, uses the next front tempo to invert in a pike position and returns to a seated position on the back tempo.
Standing to seated position to ankles to standing	Swinging trapeze	The artist drops to a seated position on the front tempo, with their ankles on the back tempo, and returns to standing on the following back tempo.
Standing to seated, full twist to ankles, return to seated position	Swinging trapeze	The artist drops to a seated position on the front tempo, performs a full twist and catches on their ankles in the back tempo and returns to a seated position on the following back tempo.
Front salto	Chinese pole	The artist performs a tempo to gain height, performs a front salto and catches the pole between their legs.
Biceps twist to catch biceps	Chinese pole	From a position holding the pole with the bicep, the artist performs full rotation horizontally toward the pole and catches the pole behind them with their elbows.
Pirouette	Chinese pole	The artist completes a full rotation vertically in parallel to the pole prior to returning to the pole.
Tempo twist to catch ball	Chinese pole	The artist performs a tempo, performs a full rotation horizontally and catches around the pole in a ball position.
Tempo climb with drop	Chinese pole	The artist climbs by jumping up the pole one leg at a time and drops.
Slack drop	Rope	The artist creates a knot with rope and releases slack to drop from one height to another.

The ANOVA revealed a significant difference between participants in all movements involving jumps in tightwire except for the seat drop in the middle of the cable (Figure 3A). The “runs” movement (mean: 2.0 BW) was 2.7 times lower than the 4 jumps movement (mean: 5.5 BW).

Maximal forces varied from 2.5 to 4.5 BW in aerial hoop for the three movements selected for the statistical analysis (Figure 3B). The ANOVA showed a significant difference between participants for all 3 movements selected in this discipline. Maximal forces ranged from 3.5 to 5 BW in swinging trapeze (Figure 3C). The results revealed significant differences only between participants for the movement involving jump. In aerial rope, participant 6 generated a mean of maximal force of 6.8 BW, whereas the mean of maximal force for participants 8, 9 and 10 combined was 4.2 BW.

The mean of maximal tension forces in cable 3 in Chinese pole presented in Figure 3F was 2.0 kN for a pretension of 1.9 kN. Forces in cable 3 were higher than that in cables 1 and 2 because of the positioning of the cables. The mean of maximal forces was 1.5 and 1.4 kN for a pretension of 1.2 and 1.1 kN for cables 1 and 2, respectively. The difference between pretension force and the mean of maximal forces is not high (maximum of 0.2 kN for cable 2). The difference between pretension force (−2.8 kN) and the mean of maximal forces (−4.6 kN) is higher (difference of 1.8 kN) for the compression force between the pole and the ground. Participants 19 and 23 generated higher compression loads (Figure 3G) compared to the other participants, whereas maximal forces were found with participant 22 for cables 1, 2 and 3 (Figures 3D, E and F).

Discussion

The main purpose of this study was to assess maximal forces in nine circus disciplines applied to rigging by acrobats performing a variety of movements. To our knowledge, our study is the first one to provide force data in swinging trapeze, fixed duo trapeze, fixed solo trapeze, Chinese pole and flying pole disciplines.

In our previous study, we found a maximal force of 5.7 BW in rope for free fall, which is lower than what we measured (7.3 BW).¹⁵ During a performance of backward long-swings, the peak tension measured in the rings cables was 8.5 BW, which is similar to what we obtained.²³ However, the backward long-swing in rings is very different from that in the rope discipline. The former involves the gymnast performing a backward rotation while maintaining a straight body, from handstand-to-handstand position, whereas for the slack drop, which is a free fall, the body remains vertical. In a previous study, we did not mention what kind of free fall we assessed.¹⁵ Slack drop is a common and relatively easy movement to execute and does not require active participation during the fall. Once the rope is set up, the only action needed is for the acrobat to let go, therefore, the only factor contributing should be the height of the fall and the mass of the acrobat (as the rope has little elasticity). It is then unexpected that one participant generated higher maximal forces than the three others. We tried to standardize the technique used by all participants, but we observed on the video recordings that participant 6 had a higher drop height because they created a bigger knot with the rope.

The maximal force measured in aerial hoop was 4.8 BW which represents an increase of 41% in comparison to a previous study.¹⁵ We reported the maximal value for a movement called “circle around the bar” in which the acrobat, leaning on the bar, does a 360° rotation without losing contact with the bar. In the current study, the maximal force was generated with a movement called “drop hip circle to front balance,” which consists of beginning with tempos and performing a backward roll around the bottom half of the hoop to finish in a front balance position. The “drop hip circle to front balance” is a little more advanced movement than the “circle around the bar” because it is more dynamic, and there is a release and catch of the bar. In the previous study, the participants in aerial hoop did not perform very dynamic movements because they mostly performed contortion figures.¹⁵ In aerial silk, the force measured in our study (5.6 BW) represents an increase of 17% relative to our previous study.¹⁵ However, the silk used was not the same. The silk from Knitrama Fabrics Inc. in our previous study is known to be more elastic than the one in this study from Beau Fab Inc., and a more elastic silk helps absorb loads.

Although there is a tension force in the cables to maintain the verticality of the Chinese pole and to tighten the cable of the tightwire, maximal force can rise up to 72% from the pretension force. Pretension and maximal forces depend on the length of the cable and the preference of the acrobat. If the tightwire distance is longer, tension force would need to be higher to achieve the same tightness. Pretension in slackline was found not to exceed 7 kN,²⁴ whereas the pretension in our study was set at 9.1 kN. However, maximal force during vertical falls with a mass of 58 kg with leash lengths of 2 and 2.5 m was measured at approximately 14 kN in slackline,²⁴ which is similar to what we measured (15 kN). Two materials were tested in slackline, high-stretch nylon and low-stretch polyester, which are much more elastic than steel cable used in tightwire. A spring was inserted in the setup of the tightwire to absorb forces, as is normally the case, but if there were no spring, forces would considerably be higher. Professionals are encouraged to use a spring in tightwire as steel cable does not elongate much. If we consider the high force generated (15 kN), anchoring points must hold these forces so that the tightwire is secured. A linear regression was used to find an equivalent vertical force in BW. The relationship between added mass and tension force was found to be linear. One limitation is that the maximal mass used to find this relationship was 220 kg, so the relationship above 220 kg is unknown. However, as the cable is rigid, the overall mechanical system is expected to be linear. With regard to the Chinese pole, the asymmetry in the setup of the cables was reflected in the forces. Cable 3, which was isolated on one side, had higher force in pretension, maximal force and mean of maximal force compared to cables 1 and 2. Forces under the pole reached a maximum of 6.3 kN. Riggers should be careful to consider maximal authorized punctual loads of the stage when installing a Chinese pole as the diameter of a pole creates a very centralized force load.

Flying pole and duo fixed trapeze generated the lowest forces. Flying pole is a more recently developed circus discipline,²⁸ and the performance is very different from other aerial disciplines. The fact that the pole is suspended in the air by one end makes it difficult for the acrobat to jump from it the way they did in traditional Chinese pole or to do free falls like in the other aerial disciplines. Given the kind of movements performed in flying pole, it is perhaps more surprising that a force of 4 BW was generated. Even in the bicep to back salto, the acrobat keeps contact with the pole with their biceps, so there is a support but not an impulse. Duo fixed trapeze is a very challenging discipline with dynamic movements. The reason for a low force measured in the cables compared to solo fixed trapeze is that the base (proximal) was in catcher’s position, that is, they had the bar in front of their hips, wrapping legs around the outside of the ropes to create a lock behind their knees. In the catcher’s position, the base was able to absorb a majority of forces from the flyer (distal). In fact, the force didn’t transmit much to the cables but was instead absorbed by the shoulders of the base. Future studies may investigate the workload and the workload–injury relationship of the proximal acrobat.

The reasons to explain the difference in the mean of maximal forces between participants are not straightforward (Figure 3). Brewin et al.²³ highlighted the importance of the gymnast’s technique and how it would potentially increase or decrease the peak force at the shoulders during backward long-swing in rings. Brewin et al.²³ claimed that if a gymnast uses a less proficient technique, they typically experience larger peak forces. In this study, almost all movements and disciplines apparatus showed a number of statistically significant inter-participant differences in cable loading. These between-participant variations may be attributed to underlying individual differences in body mechanics (strength, flexibility, coordination, smoothness, sequence of joint movements, technique, etc.) and demonstrate the potential benefits of including a larger number of participants in future circus studies. Future research could include kinematics to examine other factors that may influence forces in circus apparatuses.

The present study provided novel and valuable information, but a few limitations should be noted. Even though the current study used a small sample size per circus disciplines, the variety of movements recorded may be large enough to be representative of each discipline. Future research involving more repetitions per acrobat may generate more information on selected movements. It should be noted that the findings of this study cannot be expected to describe force production in acrobat of all levels or all sizes. We selected experienced artists who are professionals or students from professional circus schools. In addition, this study did not address the ability of the musculoskeletal system to absorb energy upon impact or to generate high forces, even though muscular activity may modify forces. The data recorded does not necessarily represent the forces the acrobat is subjected to, but the knowledge of their magnitude could be valuable to assess the risk of injury, to adapt the training and to provide a safe environment.

Requiring acrobats to perform on inappropriate circus equipment, rigging equipment or structure may have safety implications. Design factor,^14,17,18,19 dynamic factor^15,16 or safety factor^20,21,22 should reflect the real value of the force generated by the acrobat. Furthermore, the fact that there were statistical differences in dynamic loading as exhibited by many of the participants within many movements of the disciplines suggests that a larger sample size would permit to measure an even wider range in dynamic loading.

Conclusion

In summary, this is the first time that forces exerted in circus equipment are documented in swinging trapeze, duo fixed trapeze, solo fixed trapeze, Chinese pole and flying pole disciplines. Maximal forces were 4.8 BW in aerial hoop, 7.3 BW in aerial rope, 5.6 BW in aerial silk, 4.0 BW in flying pole, 5.6 BW in swinging trapeze, 6.8 BW in solo fixed trapeze and 2.5 BW in duo fixed trapeze. The maximal forces of 15 and 2.8 kN were recorded in the cable of the tightwire and in one of the cables of the Chinese pole with pretension forces of 9.1 and 1.9 kN, respectively. Ultimately, this wealth of information could be used as the basis for a recommended maximum user weight for each of the pieces of apparatus. It can help riggers and designers to make safe decisions when utilizing and fabricating circus equipment, as the ones presented in this study. However, riggers and designers should adapt their decisions to their situations, since each installation, performance and acrobat is unique. In addition, professionals need to be sure that the structure of the building can adequately support these forces. Quantification of maximal forces exerted in circus apparatuses involving high-level acrobatics potentially gives coaches and acrobats the knowledge of the performance skills and may help to develop training goals. Future research should focus on the relationship between technique through kinematics and peak forces.