Chisholm’s Paradox Revisited: Puzzles regarding Contrary-to-Duty Obligations and a Dynamic Solution

The Chisholm Set

It is not hard to imagine Jones’s normative predicament described by this set of statements. In Standard Deontic Logic, however, the Chisholm set is either inconsistent or informationally redundant. In particular, the Chisholm set is inconsistent because the following two inferences are valid in Standard Deontic Logic: (c3) and (c4) entail (c5) by Factual Detachment, and (c1) and (c2) entail (c6) by Deontic Detachment.

Apparently, (c5) and (c6) express two incompatible obligations. This is why Chisholm’s Paradox is often interpreted as a puzzle revealing the difficulty of having both detachment rules for conditional obligations, and motivates many attempts to devise a formal system that validates only one detachment rule, or validates both without the paradoxical results. Thus, it has been widely believed that ordering semantics, which does not validate both detachment rules, is free from Chisholm’s Paradox, and thus Chisholm’s Paradox has not been discussed much in the ordering semantic framework.

In this paper, I challenge this mainstream diagnosis and widely held belief about Chisholm’s Paradox. Given the Chisholm set, the most natural interpretation of Jones’s normative predicament is this: he violates his primary duty to go help his neighbors, since he does not go, and thus he ought not to tell them he is coming. By proposing a new puzzle, the CTD Trilemma, I will show that ordering semantics cannot adequately capture Jones’s normative predicament and that the real challenge raised by Chisholm’s example is not the choice between Factual Detachment and Deontic Detachment.

I argue that accurately understanding two different ways of using normative $ought$-statements is not only the key to solving the CTD Trilemma, but also the first step to developing an adequate formal semantics for normative reasoning and discourse. Based on the two principal observations about our normative reasoning and discourse using $ought$-statements, I motivate and develop a version of dynamic semantics, update semantics for normative reasoning. Finally, I show that my dynamic system solves the CTD Trilemma and adequately explains our seemingly inconsistent data about inference patterns using conditional and unconditional $ought$-statements and why the different readings of Chisholm’s example are possible.

In sum, this paper aims at making the following contributions:

1. To appreciate the real challenge raised by CTD obligations by constructing a new puzzle, the CTD Trilemma;

2. To critically evaluate the ordering semantic account of deontic $ought$-statements and conditional obligations by using the CTD Trilemma;

3. To recognize that (i) normative rules and normative judgments play distinct roles in our normative reasoning, and (ii) both are expressed by using $ought$-statements;

4. To develop a new dynamic semantics that adequately captures two different semantic functions of $ought$-statements in normative discourse and reasoning, and thereby to solve the CTD Trilemma.

In the next two sections, I briefly introduce the original puzzle, Chisholm’s Paradox for Standard Deontic Logic, and show why ordering semantics is free from this classic puzzle.

3.1. The Ordering Semantic Account of If and Ought

Ordering semantics is a broad family of semantic accounts that interpret conditionals and modals by using quantification over possible worlds and orderings over possible worlds. Ordering semantics is now an orthodox semantics in linguistics and philosophy of language, most famously developed by Angelika Kratzer and David Lewis.² The basic idea of ordering semantics is to understand modal claims as descriptions of the possibilities that are relevant in a given conversational context, and of how these possibilities are ranked relative to a given purpose.

In Kratzer’s ordering semantics, the set of accessible possible worlds and a preference ordering on them are determined by two contextual parameters: a modal base, a function $f$ mapping an index world $i$ to a set of propositions, $f\left(i\right)$, and an ordering source, a function mapping $i$ to a set of propositions, $g\left(i\right)$, that determines which possible worlds are regarded as ideal as far as that conversational context is concerned. Conditionals in ordering semantics are also modal claims. An if-clause plays the role of restricting the set of accessible possible worlds. A deontic modal claim like an $ought$-statement describes what is the case in the deontologically best possible worlds among the accessible possible worlds. Naturally, a conditional $ought$-statement describes what is the case in the deontically ideal worlds in the set of possible worlds that is restricted by the conditional’s antecedent.³

Roughly, “it ought to be that $\psi$ if $\varphi \left(\mathbf{O}\right(\psi /\varphi \left)\right)$” is true if and only if $\psi$ holds in the deontically ideal worlds among accessible $\varphi$-worlds in the given context.⁴ Here is the formal presentation of the truth condition of a conditional obligation $\left(\mathbf{O}\right(\psi /\varphi \left)\right)$ in Kratzer semantics.⁵

For a language $\mathcal{L}$ and $\mathcal{M}=〈\mathcal{W},f,g,〚\hspace{0.17em}〛〉$,

This definition reads: a conditional obligation “it ought to be that $\psi$ if $\varphi \left(\mathbf{O}\right(\psi /\varphi \left)\right)$” is true at an index world $i$ if and only if in the subset of $\varphi$-worlds accessible from $i$ the closest possible worlds to the deontic ideality determined by $g\left(i\right)$ are $\psi$-worlds. For the sake of convenience, let’s use the following simplified gloss:

$\mathbf{O}(\psi /\varphi )$ is true in $i$ iff the deontically best worlds among $\varphi$-worlds accessible from $i$ are $\psi$-worlds.

3.2. Ordering Semantics and Chisholm’s Paradox

Given the ordering semantic account of $ought$ and if, (c1)–(c3) in the Chisholm set have the following truth conditions as deontic modal statements.

It is obvious that in ordering semantics each statement of the Chisholm set provides independent information: no informational redundancy. More importantly, there is no inconsistency in this understanding of the Chisholm set. (c1) and (c2) entail $\mathbf{O}\left(t\right)$, whereas (c3) and (c4) do not entail $\mathbf{O}(\neg t)$, because Deontic Detachment is valid, but Factual Detachment is not valid in this model.

Deontic Detachment for $\mathbf{O}(\psi /\varphi )$ : $\mathbf{O}(\psi /\varphi )\wedge \mathbf{O}\left(\varphi \right)\models \mathbf{O}\left(\varphi \right)$

Factual Detachment for $\mathbf{O}(\psi /\varphi )$ : $\mathbf{O}(\psi /\varphi )\wedge \varphi \models \mathbf{O}\left(\varphi \right)$

When $\mathbf{O}\left(\varphi \right)$ and $\mathbf{O}(\psi /\varphi )$ are true, $\mathbf{O}\left(\psi \right)$ cannot be false in this system. Suppose that the deontically best worlds are $\varphi$-worlds and among $\varphi$-worlds the deontically best worlds are $\psi$-worlds. Then, the deontically best worlds are $\psi$-worlds as well. Thus, Deontic Detachment, the inference from $\mathbf{O}\left(\varphi \right)$ and $\mathbf{O}(\psi /\varphi )$ to $\mathbf{O}\left(\psi \right)$, is valid in ordering semantics. The validity of Deontic Detachment has intuitive appeal. It is natural to infer a new obligation ($\mathbf{O}\left(\psi \right)$) from a conditional obligation ($\mathbf{O}(\psi /\varphi )$) when its antecedent is obligatory ($\mathbf{O}\left(\varphi \right)$).

On the other hand, Factual Detachment is not valid for deontic modals. When it comes to deontic modals, it is obvious that an index world, $i$, is not one of the deontically best possible worlds. For example, in the actual world that we live in, filicide is morally and legally forbidden, and people ought not to commit filicide; however, the actual world is not completely free of it. The actual world is not an ideal world from a moral and legal perspective. Thus it is better not to make the assumption, called Weak Centering for deontic modals, according to which the index world $i$ is always one of the best worlds in a relevant sense.⁷ Without Weak Centering, the fact that $\varphi$ and $\mathbf{O}(\psi /\varphi )$ hold in $i$ does not guarantee that $\mathbf{O}\left(\psi \right)$ holds in $i$—it is possible that $\mathbf{O}\left(\varphi \right)$ is false in $i$. Therefore, Factual Detachment is invalid in ordering semantics. As a result, (c5) does not follow from (c3) and (c4), whereas (c6) does follow from (c1) and (c2). There is no inconsistency in the Chisholm set.

In sum, ordering semantics is free from the paradoxical results of the Chisholm set that we saw in SDL thanks to its new understanding of the meaning of conditionals and the invalidity of Factual Detachment.

4.1. Three Interpretations of Chisholm’s Example

First, the According-to-Duty (ATD) Situation of the Chisholm’s example is a situation in which Jones has not gone help his neighbors yet, but it is still practically possible for him to go help them. Suppose, for example, that Jones is out of town and knows that his weekend will be well-spent if he goes help his neighbors move tomorrow. Imagine that he can still go help them tomorrow if he catches the train back to town tonight. In this situation, what he ought to do is to go help his neighbors and let them know he is coming. In the ATD situation, (c1)–(c4) hold and the derived ought-statement (c6) holds, but not (c5).

Second, the Overriding Situation is a situation where it would be a good thing for him to go help his neighbors, but it is outside his ability; so it is not the case that he ought to go help them. For example, suppose that Jones is out of town and knows that his neighbors need his help tomorrow, but he has already missed all trains back to town (or, there’s no train back to town due to the bad weather); so he won’t be there to help them in time. Given Jones’s predicament it cannot be said that Jones ought to go help his neighbors; he ought not to tell them he is coming. In the Overriding Situation, (c2)–(c5) hold in this situation, but (c1) does not. It is easy to see that the critical feature that distinguishes the ATD Situation and the Overriding Situation is Jones’s practical ability to go help his neighbors.

Third, the CTD Situation is a situation in which Jones violates his duty and his CTD obligation takes effect. That means he ought not to tell them he is coming, but the duty he has failed to fulfill is still there as his duty. Imagine, for example, that Jones has a duty to help his neighbors as a community member or as part of his job (e.g., as a firefighter) and his neighbors need his help. However, Jones missed the last train that would get him back to town in time. He won’t be able to help his neighbors. So he ought not to tell them he is coming. However, it is true at the same time that he ought to go help his neighbors since that’s his duty. Although (c1) and (c2) express Jones’s duties and obligations, we should not infer that Jones ought to tell his neighbors he is coming. Therefore, (c1)–(c5) hold in the CTD Situation, but not (c6).

The CTD Situation is importantly different from the Overriding Situation in that (c1) is read as expressing Jones’s duty or obligation in the CTD Situation, which persists regardless of his practical ability of fulfilling the duty in the current circumstance. The Overriding Situation is the interpretation of the Chisholm set when reading (c1) as a judgment that tells Jones which act or course of action is the best thing to do in a relevant sense given his current situation, like recommendation or advice. And, that is why (c1) stops holding when (c4) is true.

Clarifying these three possible interpretations of Chisholm’s example permits us to see that depending of how we interpret Jones’s normative predicament Chisholm’s example presents different challenges with different sets of statements to work on in a formal account.

There have been many attempts to deal with Chisholm’s Paradox by carefully attending to temporal or agential components of the example. These attempts, roughly, argue that since it is time-sensitive whether Jones can fulfill (c1), what Jones ought to do is different before and after a certain critical point of time that determines whether he can go help his neighbors or not: the ATD Situation before this point and the Overriding Situation after the point. Therefore, Jones’s predicament in Chisholm’s example is either the According-To-Duty (ATD) Situation or the Overriding Situation.

Given this dichotomic interpretation of Chisholm’s example, neither the clash between (c5) and (c6) nor the tension between (c1) and (c5) arise, because they simply do not hold at the same time for Jones. If this interpretation of Chisholm’s example is correct, formal frameworks for $ought$s and if s are lifted from the burden of reconciling Factual Detachment and Deontic Detachment, and the challenge raised by Chisholm’s example is to devise a formal system that is sensitive to such temporal aspects or agent’s abilities and can capture both the ATD and Overriding Situations.

Proponents of ordering semantics would welcome this interpretation of Chisholm’s example, since the relation between the truth of (c1) and Jones’s ability to go is easy to capture using the ordering semantic framework. Here’s how that goes. It is a logical truth that either Jones can go help his neighbors, or Jones cannot go help his neighbors: $\diamond h\vee \neg \diamond h$. According to the standard ordering semantic account of modals and conditionals, $\diamond h$ is true at $w$ iff there is at least one h-possible world accessible from $w$. On the other hand, $\neg \diamond h$ is true at $w$ iff there is no $h$-world among all the possible worlds accessible from $w$. Therefore, the two possible situations are captured by different modal bases: $\neg h\notin f_1$ and $\neg h\in f_2$, respectively. Suppose that the relevant ordering source is $g=\left\{h,h\supset t,\neg h\supset \neg t\right\}$. In the situation where Jones can go $\left(\diamond h\right)$, the relevant contextual parameters are $f_1$ and $g$. Given $f_1$ and $g$, there are some $h$-worlds in the relevant domain, and $h$-worlds are the deontically best worlds. Therefore, Jones ought to go help his neighbors and tell them he is coming : (c1) $\wedge$ (c6). On the other hand, in the situation where Jones cannot go to help his neighbors $\left(\neg \diamond h\right)$, the relevant contextual parameters are $f_2$ and $g$. Given $f_2$ and $g$, there are no $h$-worlds in the relevant domain. Among $\neg h$-worlds, $\neg h\wedge \neg t$ -worlds are better than $\neg h\wedge \neg t$-worlds. Therefore, Jones ought not to tell them he is coming ($\mathbf{O}(\neg t)$); but, importantly, it is not the case that he still has an obligation to go help his neighbors ($\neg \mathbf{O}\left(h\right)$).⁸

Although the dichotomic interpretation is possible for Chisholm’s example, it is easy to construct examples of Chisholm’s Paradox without temporal and agential components. Here’s Prakken and Sergot’s (1996) example:

Unlike (c1) in the Overriding Situation, (d1) is neither defeated nor overridden in this timeless example. From (d1)–(d4) it follows that there ought to be a warning sign, but (d1) still holds as a holiday cottage regulation. Regardless of whether or not a dog can be removed, (d1) holds as a holiday cottage regulation, and (d1) is violated given the truth of (d4). It seems that the most natural reading of (d1)–(d4) is the CTD Situation. So we should conclude that the real puzzle invoked by Chisholm’s example is not about temporal or agential components in normative discourse.

Moreover, both the ATD Situation and the Overriding Situation lack the characteristic twofold mechanism of a CTD obligation: the violation of a primary obligation and the generation of a new obligation upon the violation. In the ATD Situation, the CTD obligation does not take effect. In the Overriding Situation, there is no violation of Jones’s primary obligation or duty since (c1) stops being relevant as being overridden by (c4), in other words, the situation where (c4) is an exceptional situation for (c1), where (c1) does not hold. However, the situation in which a CTD obligation takes effect is a sub-ideal situation, not an exceptional circumstance. In other words, when his CTD obligation takes effect, Jones’s primary obligation is violated, not replaced by some other new obligation. Among the three interpretations of Chisholm’s example, the CTD Situation is the only interpretation that captures the characteristic twofold mechanism of our reasoning with a CTD obligation. Let’s take a close look at the CTD Situation.

4.2. The CTD Situation and The CTD Trilemma

Here are three characteristic features of the CTD Situation: (I) and (II) are the two features that distinguish the CTD Situation from the ATD Situation and the Overriding Situation, and (III) says that the CTD Situation is not an aberrant normative situation like a dilemma situation.

I. Violation of a Primary Obligation

In the CTD Situation, the relevant agent’s primary obligation holds, but it is violated: $\mathbf{O}\left(\varphi \right)\wedge \neg \varphi$.

II. Inference of a New Ought-Statement

In the CTD Situation, a new $ought$-statement that tells the agent what to do in her current circumstance is derived from a CTD obligation and factual statement: $\mathbf{O}\left(\psi \right)$ from $\neg \varphi$ and $\mathbf{O}(\psi /\neg \varphi )$.

III. No Tension among Ought-Statements

Conditional and unconditional $ought$-statements in the CTD Situation do not generate contradictory or difficult normative choices for the agent; the agent in the CTD Situation does not face a practically difficult choice.

These three characteristic features of the CTD Situation are also the three requirements a satisfactory formal account of $ought$ and $if$ must meet: (I) the Violation Requirement, (II) the New $Ought$-Statement Requirement and (III) the No Tension Requirement. In Chisholm’s example, together with the first two requirements, (III) the No Tension Requirement put constraint on what we should not infer from the Chisholm set in the CTD Situation.

1. (c6) does not follow from (c1) and (c2), or even if (c6) follows from (c1) and (c2), it is not the case that Jones ought to tell and not tell he is coming;

2. (c1) and (c5) hold, but it is not the case that Jones ought to go help and not tell them he is coming.

Let’s call the challenge of meeting all three features of the CTD Situation the CTD Trilemma. Meeting all three of them amounts to representing Jones’s CTD situation as the situation in which (c1)–(c5) hold but (c6)–(c8) do not hold. Let’s call this set of statements (c1)-(c5) that represent Jones’s CTD Situation, the Extended Chisholm set.

The CTD Trilemma specifies the three desiderata a formal account of normative language must meet. They strongly suggest the validity of Factual Detachment and the invalidity of Deontic Detachment and Agglomeration of $ought$-statements. Any satisfactory formal account must be able to explain these puzzling data points and formally incorporate them. Now the question is whether this new puzzle can solved in the ordering semantic framework.

First, a version of ordering semantics that rejects Weak Centering can express the violation of Jones’s primary obligation by using the conjunction $\mathbf{O}\left(h\right)\wedge \neg h$. However, the rejection of Weak Centering results in the invalidity of Factual Detachment as we have seen in Section 3.2.⁹ Thus, this version of ordering semantics has difficulty in explaining why it is natural to infer the new $ought$-statement (c5) in the CTD Situation. Therefore, this approach meets (I) the Violation Requirement and (III) the No Tension Requirement, but fails to meet (II) the New Ought-Statement Requirement.

Second, a version of ordering semantics that assumes Weak Centering for deontic modals runs a different risk. This version of ordering semantics validates Factual Detachment since it assumes that the actual world is one of the ideal possible worlds when evaluating deontic modals. So it meets (II).¹⁰ However, the conjunction $\mathbf{O}\left(h\right)\wedge \neg h$ is not possible in this system, since the truth of $\mathbf{O}\left(h\right)$ entails the truth of $h$ in $i$ given Weak Centering. Therefore, this version of ordering semantics with Weak Centering meet (II) and (III) but fail to meet (I). In sum, whether or not Weak Centering is assumed, ordering semantics faces unwanted results: if Weak Centering is assumed, then it fails to meet (I) the Violation Requirement; and if not, it fails to meet (II) the New $Ought$-Statement Requirement.

Since the rejection of Weak Centering entails the invalidity of Factual Detachment, it would look like a problem of how to make sense of Factual Detachment in the ordering semantic framework without giving up on our strong intuition that the actual world is not a deontically ideal world. Let’s check this route. Inspired by Stalnaker (1975), one might argue that Factual Detachment is technically invalid, but pragmatically valid in that the inference of $\mathbf{O}\left(\psi \right)$ from the assertions of $\mathbf{O}(\psi /\varphi )$ and $\varphi$ is reasonable.¹¹ Since Deontic Detachment is valid in ordering semantics, the pragmatic validity of Factual Detachment brings the familiar tension between (c5) and (c6) back. At least, this approach must explain why (c5) guides Jones’s action, while (c6) does not.

Maybe we can concoct a version of ordering semantic account for oughts and ifs that invalidates Deontic Detachment but validates Factual Detachment, and get the positive data right: (c5) follows from (c1)–(c4), but not (c6). This will meet both (I) and (II). Unfortunately, even this contrived system cannot meet (III). Just (c1) and (c5) together generate a tension in an ordering semantic framework, which does not exist in our intuitive understanding of the CTD Situation. To say that both (c1) $\mathbf{O}\left(h\right)$ and (c5) $\mathbf{O}(\neg t)$ are true means that in the deontically ideal possible worlds Jones goes help his neighbors but does not tell them he is coming in the ordering semantic framework. Although (c1) and (c5) are not logically inconsistent with each other, $\mathbf{O}(h\wedge \neg t)$ does not hold in the CTD Situation given that (c1) and (c2) hold in the CTD Situation; according to (c1) and (c2), ideally Jones is supposed to go help his neighbors and tell them he is coming. Prakken and Sergot (1996; 1997) call this puzzling result in ordering semantics Pragmatic Oddity. Saint-Croix and Thomason (2016) also draw attention to the tension between (c1) and (c5) in Chisholm’s example. They argue that with or without conditional $ought$-statements in the Chisholm set (c1) and (c5) generate a puzzle; both (c1) and (c5) hold in Chisholm’s example, but the conjunction of them, (c7), “is clearly false” (Saint-Croix & Thomason 2016: 193). They call this puzzle, an unconditional version of Chisholm’s Paradox.¹²

In sum, the three characteristic features of the CTD Situation generate the following trilemma for ordering semantics:

The CTD Trilemma

The ordering semantic account of $ought$s and ifs can meet two of the three features of the CTD Situation, but not all three of them. Therefore, it fails to provide a faithful formal representation of the CTD Situation.

The discussion so far and the exploration of possible solutions to the CTD Trilemma in the ordering semantic framework naturally prompts us to suspect that (c1) and (c5) are different types of $ought$-statements and nudge us to explore alternative approaches.

5.1. Normative Rules and Normative Judgements

The distinction between normative rules and normative judgments is straight-forward. By normative rules, I mean regulative rules in our lives that offer guidance for judgments about what to do in various circumstances. Moral, civil, or legal duties and obligations, requirements of etiquette and social norms all are considered normative rules. On the other hand, a normative judgment is a practical judgment inferred from a set of normative rules and facts telling us which course of action is most desirable in the given circumstance.

Normative rules are prescriptive in that they generate commitments and expectations to perform, avoid, or permit certain types of acts. A set of normative rules that are accepted by an agent forms a preference pattern regarding which courses of action or states of affairs are most desirable. For example, for those who have learned and internalized a set of dinner manners, eating asparagus with their fingers is considered more desirable than eating asparagus with a knife and fork. For Kantian deontologists, being completely honest is always morally preferable to lying.

Normative rules are importantly different from empirical rules that express causal or empirical regularities. A case that does not conform to a certain empirical rule challenges or even disproves the empirical rule, but a particular case that does not conform to a normative rule is a violation of the rule and does not weaken the rule. For example, the observation of white ravens would challenge the empirical rule that all ravens are black; on the other hand, lying to a murderer outside your door to disallow him entrance into your home would be a violation of the moral principle not to lie but does not challenge or disprove it.¹³

The contrast between normative rules and empirical rules reveals another important attribute of normative rules. Normative rules remain relevant as regulative rules even when an agent violates them, unless an agent is exempted from them or stops being the subject of the rules. As a legally recognized subject of her country, for example, Jane has an obligation to serve on a jury when called. Suppose that Jane was called. “Jane ought to serve on a jury” as a normative rule holds, and does so even when she fails to show up for the duty. She can be exempt from her jury service if she meets certain conditions, but that exemption does not dissolve her duty as a citizen.¹⁴

In contrast to a normative rule, a normative judgment tells us what action or state of affairs is more desirable than its alternative. Normative judgments as practical judgments are sensitive to the agent’s contingent circumstances and her practical abilities in a given situation and guide her actions, and can change as the circumstances change. An agent makes a normative judgment based on her factual judgments (what is known) about her current circumstance and the conditional and unconditional normative rules accepted by her. A devoted utilitarian would make a normative judgment “I ought to give more money to charity” from a combination of his moral principles and the facts regarding his income and necessary living expenses. When I fail to keep my promise to my partner, “I ought to apologize to my partner” is the normative judgment I infer from a given set of normative rules I accept and the fact that I failed to keep my promise.

Now we have an intuitive model of a simple normative reasoning using normative rules, normative judgments, and factual judgments. Conditional or unconditional normative rules structure the pattern of preferences by imposing obligations, granting permissions, and forbidding certain types of actions, and facts (or what is known) about the given circumstance determines what are practically feasible choices in the circumstance. A normative judgment is made by using both the pattern of preferences defined by normative rules and the set of choices limited by what is known about the given circumstance. For example, my moral duty to keep my promise to my partner generates the preference ranking over two states: keeping my promise over not keeping my promise. My conditional obligation to apologize when failing to keep my promise articulates the preference ranking further in the following order : 1) keeping my promise; 2) failing to keep my promise and apologizing for it, and 3) failing to keep my promise and not apologizing. When keeping my promise is still a possibility, I ought to keep my promise. When I fail to keep my promise, I have only two options: apologizing for it or not apologizing for it. And, my normative judgment has to be: “I ought to apologize.” Even in this sub-ideal situation, my duty to keep my promise holds. In other words, my primary moral duty “I ought to keep my promise” holds.

Now is the time to talk about the second principle of this approach: even though they serve different functions in our normative reasoning, both normative rules and judgments can be expressed by $ought$-statements in our normative discourse.¹⁵ Imagine Jane is called for jury duty, and suppose it turns out that she was a victim in a similar crime and knows that it will be hard for her to maintain objectivity. In this case, she can reasonably make a normative judgment “I ought not to serve on a jury,” although this judgment is opposed to the relevant normative rule, which also could be stated in a form of $ought$-statement: “Jane ought to serve on a jury.”

Here I argue that $ought$-statements used in normative discourse that are commonly believed to be homogeneous are actually of two kinds: one expressing normative rules and the other expressing normative judgments. And their functions in our normative discourse and reasoning are distinct enough to be taken into our semantic account of $ought$-statements. The question of how to disambiguate two meanings of $ought$-statements in normative discourse in various contexts is beyond the scope of this paper. For the purposes of my project, I am going to presume this ambiguity is resolved at the pragmatic level and focus on analyzing their semantic contents. From now I am going to use two different operators, one for $ought$-statements expressing normative rules (${\mathbf{O}}_R$) and the other for $ought$-statements for normative judgments (${\mathbf{O}}_J$). In texts, I will use the subscripts to indicate different kinds of $ought$s: “${\text{ought}}_R$” and “${\text{ought}}_J$.”

5.2. A Sketch for a New Solution to the CTD Trilemma

Using the three components of normative reasoning and the dual nature of $ought$-statements we can give a natural explanation of Jones’s normative predicament in the CTD Situation. In the CTD Situation, (c1)–(c3) are the normative rules for Jones. (c1) expresses Jones’s duty as a community member; (c2) expresses Jones’s conditional obligation stemming from common etiquette; and (c3) expresses Jones’s CTD obligation related to a general obligation not to to lie or deceive others. (c4) is the factual judgment about Jones’s contingent situation. (c5) is the normative judgment derived from his CTD obligation and factual judgment, (c3) and (c4).¹⁶ So the Extended Chisholm Set describing Jones’s normative predicament in the CTD Situation actually consists of the three different types of statements as follows:

We can informally illustrate how the normative rules, the factual statement and the normative judgments in the CTD Situation interact in the CTD Situation with diagrams. The three normative rules, (c1)–(c3), define Jones’s normative preference over possible worlds (or possible states of affair) as follows: (Solid-line circles represent possible worlds that are not ruled out, while dashed-line circles represent possible worlds ruled out by what is known; the arrow connecting two circles or boxes indicates which possibility is preferred; what an arrow is pointing to is the preferred possibility between two possibilities that the arrow connects.)

The factual statement (c4) defines what are practically possible options for Jones in his current predicament by ruling out all $h$-worlds from the set of possible worlds as in the following diagram.

Given (c1)–(c4), the normative judgment (c5) “Jones ${\mathit{ought}}_J$ not to tell them he is coming” accurately describes the best Jones can do in the given circumstance. This new reading of the Extended Chisholm set suggests an intuitive solution to the CTD Trilemma. The simple conjunction of (c1) and (c4), ${\mathbf{O}}_R\left(h\right)\wedge \neg h$, expresses the violation of Jones’s primary obligation to help his neighbors. The normative judgment ${\mathbf{O}}_J(\neg t)$ follows from the Chisholm set in that $\neg h\wedge \neg t$-worlds are the most preferred worlds when (c4) holds, as in the diagram. Finally, the normative rule (c1) ${\mathbf{O}}_R\left(h\right)$ and the normative judgment (c5) ${\mathbf{O}}_J(\neg t)$ are not in conflict and thus can be true in the same situation. As we have seen, what is expected by a normative rule does not always coincide with the best we can do in a particular situation, and a normative rule holds even when violated.

This new approach provides a simple intuitive explanation of why (c6)–(c8) all are false normative judgments.

From the normative rules (c1)–(c3) and the factual judgment (c4), the normative judgment (c6) simply does not follow and is neither one of Jones’s normative rules nor an adequate normative judgment in the CTD Situation. Since (c1) is a normative rule and (c5) is a normative judgment, we cannot, using Agglomeration, combine them into one $\mathit{ought}$-statement, which explains the falsity of (c7) without invalidating Agglomeration.

In addition to this natural, intuitive account of the CTD Situation, this new reading can explain why different interpretations of Chisholm’s example are possible. In particular, when Chisholm’s example is read as the Overriding Situation, we read (c1) as a normative judgment overridden by a newly derived normative judgment (c5), because a normative judgment is sensitive to a factual judgment. As a situation changes, an adequate normative judgment may change.

In this section, above, I have proposed a new reading of the Extended Chisholm set and a new approach to the CTD Trilemma, using two key observations: (i) normative rules and normative judgments have distinct functions in our normative reasoning and (ii) $\mathit{ought}$-statements can express both normative rules and judgments in our normative discourse. With these two principles, we can provide a natural explanation of the CTD Situation and meet the three desiderata of the CTD Trilemma in a natural and unforced manner. In the next section, I will develop a new semantic account for normative reasoning that formally captures these principles, thus solving the CTD Trilemma.

6.1. Veltman’s Update Semantics

The core idea of dynamic semantics is that the meaning of a sentence is how it changes the context or what is believed or accepted by its participants. This context or conversational common ground is called an information state, which is formally represented by a set of possible worlds.¹⁷ In static systems, to know the meaning of “it’s raining” is to know when “it’s raining” is true. In the dynamic framework, to know the meaning of “it’s raining” is to know what kind of changes it brings to a relevant agent’s information state who accepts the information conveyed by the sentence. Since what is believed or accepted as true is a central part of a context, the dynamic semantic meaning of a sentence is often called a “context change potential” (CCP), which is a function from one information state to another.¹⁸

Without much formalism, we can easily understand how update semantics defines the meaning of simple statements ($\varphi$) and epistemic $\mathit{might}$-statements $\left({\diamond }_e\varphi \right)$ and introduce some core concepts of dynamic semantics. Suppose Ben is wondering if it’s snowing outside and naturally says “it might be snowing outside $\left({\diamond }_{e}p\right)$.” Abby tells him “it’s not snowing ($\neg p$).” Her utterance changes what Ben believes in that Ben stops believing what is incompatible with what he has learned. So after accepting Abby’s utterance it is inadequate for him to say or accept “it might be snowing outside $\left({\diamond }_{e}p\right)$.” This process of incorporating new information into a current information state to evolve a new information state is called an update. When a certain information state ($\sigma$) is already compatible with $\varphi$, $\varphi$ is accepted in $\sigma$ (or, $\sigma$ supports $\varphi$). In this example,“it might be snowing outside” was accepted in Ben’s information state before Abby’s utterance of $\neg p$, but not after the update with $\neg p$. This change shows that the process of updating new information is not monotonic. While accepting Abby’s utterance “it’s not snowing ($\neg p$)” amounts to ruling out the possibilities of snowing ($p$) from Ben’s information state, accepting an epistemic $\mathit{might}$-statement does not require a change in the information state. The utterance of “it might be snowing $\left({\diamond }_{e}p\right)$” would be accepted only when the possibility of snowing is not completely rules out. The different behaviors of simple statements and epistemic $\mathit{might}$-statements reveal the important distinction between two kinds of updates in a dynamic account: “additive propositional updates and non-classical tests” (Veltman 1996: 5). An utterance of $\varphi$ in a discourse requires updating the relevant information state with $\varphi$ by ruling out the possibilities incompatible with it, while an utterance of $\mathit{might}\left(\varphi \right)$ is an invitation to perform a test on the information state, checking whether the information state is compatible with the possibility of $\varphi$.¹⁹

Here is a formal presentation of this basic update semantics for simple statements and epistemic $\mathit{might}$-statements.

Definition 1 (Languages, $L_0^{\mathcal{A}}$ and $L_1^{\mathcal{A}}$) Let $\mathcal{A}$ be a set of atomic sentences, $p,q,r,\dots$. The language $L_0^{\mathcal{A}}$ has $\mathcal{A}$ as its non-logical vocabulary and the logical operators, such as $\neg$, $\vee$, and $\wedge$, and parentheses,) and (, as its basic logical vocabulary.

A string of symbols $\chi$ is a sentence of $L_0^{\mathcal{A}}$ iff

1. for some atomic sentence $p\in \mathcal{A}$, $\chi =p$;

2. for some sentence $\varphi$ of $L_0^{\mathcal{A}}$, $\chi =\neg \varphi$;

3. for some sentences $\varphi$ and $\psi$ of $L_0^{\mathcal{A}}$, $\chi =\varphi \wedge \psi$;

4. for some sentences $\varphi$ and $\psi$ of $L_0^{\mathcal{A}}$, $\chi =\varphi \vee \psi$.

A language $L_1^{\mathcal{A}}$ has $\mathcal{A}$ and its logical vocabulary and an additional unary operator ${\diamond }_e$ for $\mathit{might}$.

A string of symbols $\chi$ is a sentence of $L_1^{\mathcal{A}}$ iff for some sentence $\varphi$ of $L_0^{\mathcal{A}}\hspace{0.17em}\chi =\varphi$ or $\chi ={\diamond }_e\varphi$

Definition 2 (The Space of Possible Worlds, $\mathit{W}$) Let $W$ be the set of all possible worlds, $w$. Each possible world $w$ is an atomic valuation, a function from every atomic sentence in $\mathcal{A}$ to one truth value $(\mathbf{1},\mathbf{0})$.

Definition 3 (Truth Sets/Propositions) For $p\in \mathcal{A}$, ${〚p〛}^M=\left\{w\in W|w\left(p\right)=1\right\}$. $〚p〛$ is a set of possible worlds in which $p$ is true. (A model $M$ will be omitted for simplicity.)

Definition 4 (Information State) (i) $\sigma$ is an information state iff $\sigma \subseteq W$; (ii) $\mathbf{0}$, the minimal state, is the information state given by $W$; (iii) $\mathbf{1}$, the absurd state, is the information state given by the empty set.

For any sentence $\varphi$, $\mathbf{1}\left[\varphi \right]=\mathbf{1}$. That means, in the absurd state every sentence is accepted, but no sentence is acceptable.

Definition 5 (Update System) An update system is a triple $〈L,\Sigma ,[\ast ]〉$, where $L$ is a language, $\Sigma$ is a set of information states, $\sigma$, each of which is a subset of $W$, and $[*]$ is an update function. For any system $M$, an update function $[*]$ is a function from a sentence of $L$ to functions from information states to information states in $\Sigma$.

Definition 6 (Update Function) For $p\in \mathcal{A}$ and $\varphi$ and $\psi$ of $L_0^{\mathcal{A}}$, any sentence $\chi$ of $L_1^{\mathcal{A}}$ is such that $\chi =p;=\neg \varphi ;=\varphi \wedge \psi ;=\varphi \vee \psi$; or $={\diamond }_e\varphi$. For any $\chi$ of $L_1^{\mathcal{A}}$ and an information state $\sigma$, $\sigma \left[\chi \right]$ is determined as follows:

While updating the information state $\sigma$ with $p$ has the effect of excluding all $\neg p$-worlds from $\sigma$, the function of epistemic modal statement behaves like a test. Updating $\sigma$ with ${\diamond }_{e}p$ returns $\sigma$, if there is at least one $p$-world in $\sigma$; otherwise, it is an absurd state, $\mathbf{1}$, given by the empty set.

Another central idea of a dynamic framework is the notion of acceptance. $\varphi$ is accepted in an information state $\sigma$ when updating $\sigma$ with $\varphi$ does not change $\sigma$: $\sigma \left[\varphi \right]=\sigma$. In other words, such $\sigma$ supports $\varphi$; $\sigma$ is called the fixed point of $\varphi$.

Definition 7 (Acceptance)

Consequence in a dynamic system can be defined in terms of acceptance as follows.

Definition 8 (Dynamic Consequence)

This dynamic definition of consequence means that ${\varphi }_1,\dots ,{\varphi }_n\models \psi$, just in case every state of information which is a fixed point of $\left[{\varphi }_1\right]\dots \left[{\varphi }_n\right]$ also supports $\psi$. The dynamic notion of consequence as the preservation of acceptance is non-monotonic in that it is sensitive to the order of premises.

6.2. Default Reasoning and Normative Reasoning

Veltman (1996) expands this simple model of update semantics to analyze default reasoning with default rules expressed by “normally (or usually) $\varphi$” and expectations expressed by “presumably $\varphi$.” Default rules, such as “normally, ravens are black” and “normally, cold sores heal in a week by themselves,” are descriptive rules that serve to express empirical regularities. They help us get to reasonable expectations or guesses about what will happen. For example, “presumably, Julia’s new pet raven is black”; and “presumably, Jake’s cold sore will heal in a week.” Restricted default rules expressed in the conditional form allow us to make more precise expectations or guesses; for example, “if the patients do not get enough lysine from their diet, cold sore remedies normally take more than a week.”

Suppose that normally the campus bookstore is busy in the afternoon. Given this knowledge, it is reasonable for one to conclude that presumably the campus bookstore is busy this afternoon. Suppose that you have found that it’s pretty empty this afternoon. Still you can say, “normally, the campus bookstore is busy in the afternoon,” but once seeing it’s not busy, it is not apt anymore to say, “presumably, the campus bookstore is busy.” This example instantiates the following characteristic inference patterns between “normally $\varphi$,” “presumably $\varphi$” and “$\varphi$.”

Suppose that the following conditional default rule holds about the campus bookstore as well: “if the campus bookstore is not busy in the afternoon, normally there is a school event.” You have found that the bookstore is not busy this afternoon. Given these default rules and finding, you can infer: “presumably, there is a school event.” Again, the default rule, “Normally, the campus bookstore is busy in the afternoon” holds. The following utterance is true and felicitous to utter:

“The bookstore is not busy this afternoon. Presumably, there is a school event. However, normally, the campus bookstore is busy in the afternoon.”

Thus, the following inferences regarding non-conforming cases and conditional default rules are warranted in default reasoning.

The interplay among default rules, expectations and factual judgments in default reasoning is parallel to the one among normative rules, normative judgments and factual judgments in normative reasoning. Accepted default rules generate a pattern of expectations regarding what will more likely happen. Likewise, accepted normative rules generate a pattern of preferences regarding what actions or state of affairs is more desirable. A default rule holds even when a particular occasion or circumstance diverges from what the default rule predicts. Similarly, a normative rule holds even when it is violated on a particular occasion.

The following inferences using normative rules, normative judgments and factual judgments are naturally warranted in normative reasoning.

These two sets of inferences, (d1)–(d5) and (n1)–(n5), manifest the structural parallelism between default reasoning and normative reasoning and show why it is natural to adapt Veltman’s update semantics for default reasoning to model normative reasoning using normative rules and normative judgments.

6.3. The Dynamic Meanings of Ought-Statements

To formally represent the distinctive functions of two kinds of $\mathit{ought}$-statements in dynamic semantics, we need a structured information state that can capture two things: what an agent knows and an agent’s normative preference pattern over possibilities. These two attributes of a structured information state can be modeled by a set of possible worlds and a preference ordering pattern over the possible worlds. Now we can articulate the meanings of ${\mathbf{O}}_R(\psi /\varphi )$ and ${\mathbf{O}}_J(\psi /\varphi )$ in terms of how they contribute to a structured information state $\sigma$. The meaning of a normative rule expressed by ${\mathbf{O}}_R(\psi /\varphi )$ is its potential to change the preference ordering of possible worlds in the set of all $\varphi$-worlds of $\sigma$ in a way that all -worlds are preferred over (or ranked higher than) -worlds. On the other hand, the meaning of a normative judgment expressed by ${\mathbf{O}}_J(\psi /\varphi )$ is its potential to test whether all -worlds are preferred over -worlds in the current information state $\sigma$.

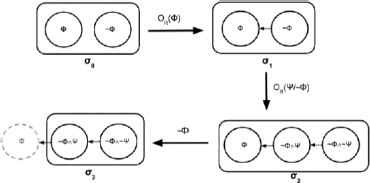
Before presenting formal definitions let me illustrate what their updates would look like with a diagram.

Figure 1

Suppose that a structured information set ${\sigma }_0$ is represented by a set of all possible worlds $W$ and no preference ordering. Updating ${\sigma }_0$ with a normative rule ${\mathbf{O}}_R\left(\varphi \right)$ and a conditional normative rule ${\mathbf{O}}_R(\psi /\neg \varphi )$ in order has the effect of generating the preference pattern as in ${\sigma }_2$, and updating $\neg \varphi$ has the effect of ruling out all $\varphi$-worlds as in ${\sigma }_3$. (Again, in diagrams solid-line circles represent sets of possible worlds; the circle an arrow points to is a preferred possibility; and gray dashed-line circles are the sets of possibilities that are ruled by propositional updates.)

We can easily understand the different types of updates by ${\mathbf{O}}_R(\psi /\varphi )$, ${\mathbf{O}}_J(\psi /\varphi )$ and $\varphi$ in this diagram. Updating with a conditional normative rule ${\mathbf{O}}_R(\psi /\neg \varphi )$ generates a new preference pattern in the set of $\neg \varphi$-worlds. These information statements support different normative judgments; in other words, different normative judgments hold as the information state changes. Both ${\sigma }_1$ and ${\sigma }_2$ support ${\mathbf{O}}_J\left(\varphi \right)$, but not ${\sigma }_3$. Both ${\sigma }_2$ and ${\sigma }_3$ support the conditional normative judgment ${\mathbf{O}}_J(\psi /\neg \varphi )$; ${\sigma }_3$ even supports the unconditional normative judgment ${\mathbf{O}}_J\left(\psi \right)$ because $\psi$-worlds are the best worlds in ${\sigma }_3$. That means an agent in an information state ${\sigma }_1$ or ${\sigma }_2$ makes a normative judgment that it ought to be that $\varphi \left({\mathbf{O}}_J\right(\varphi )$); however, an agent in ${\sigma }_3$ does not make the normative judgment because the possibility of $\varphi$ is ruled out by what is known ($\neg \varphi$). While adequate normative judgments change as the information state evolves, the normative rule ${\mathbf{O}}_R\left(\varphi \right)$ remains accepted in the information state; that is, all three information states ${\sigma }_1$, ${\sigma }_2$, and ${\sigma }_3$ support ${\mathbf{O}}_R\left(\varphi \right)$.

In the next subsection, I will formally present my update semantics for normative reasoning that captures the dynamic meanings of the three types of statements and their interplay summarized in (n1)–(n5). The formal strategy of my update semantics for normative reasoning largely follows Veltman’s approach with some stylistic modification and simplification because in this paper I do not deal with rules with exceptions.

6.4. Update Semantics for Normative Reasoning

The major work we need to do to expand the simple update semantics into update semantics for normative reasoning is to construct a structured information state that can keep track of the changes by both normative rules and factual statements. With a structured information state, we will be able to define the two new operators ${\mathbf{O}}_R(\psi /\varphi )$ and ${\mathbf{O}}_J(\psi /\varphi )$ in a way that captures their meanings illustrated with the diagrams and the inference patterns (n1)–(n5).

Definition 9 (Normative Language $L_2^{\mathcal{A}}$) Let $\mathcal{A}$ be a set of atomic sentences, $p,q,\dots$. The language $L_0^{\mathcal{A}}$ has $\mathcal{A}$, as its non-logical vocabulary and the logical operators, such as $\neg$, $\vee$, and $\wedge$, and parentheses,) and (, as its basic logical vocabulary.

A string of symbols $\varphi$ is a sentence of $L_0^{\mathcal{A}}$ iff

1. for some atomic sentence $p\in \mathcal{A}$, $\varphi =p$;

2. for some sentence $\psi$ of $L_0^{\mathcal{A}}$, $\varphi =\neg \psi$;

3. for some sentences $\psi$ and $\chi$ of $L_0^{\mathcal{A}}$, $\varphi =\psi \wedge \chi$;

4. for some sentences $\psi$ and $\chi$ of $L_0^{\mathcal{A}}$, $\varphi =\psi \vee \chi$.

A language $L_2^{\mathcal{A}}$ has two additional dyadic operators: ${\mathbf{O}}_R$(−/−) and ${\mathbf{O}}_J$ (−/−).

A string of symbols $\chi$ is a sentence of $L_2^{\mathcal{A}}$ iff for sentences $\varphi$ and $\psi$ of $L_0^{\mathcal{A}}$, (i) $\chi =\varphi$; or (ii) $\chi ={\mathbf{O}}_R(\psi /\varphi )$ or $\chi ={\mathbf{O}}_J(\psi /\varphi )$.

In order to introduce a structured information state, we need to define two formal devices: a frame $N$ on $W$ and a preference pattern $N\left(d\right)$ on $d$.

Definition 10 (Frame) Let $W$ be the power set of the set A of atomic sentences. A frame $N$ on $W$ is a function assigning a preference pattern $N\left(d\right)$ on $d$ for every $d\subseteq W$.

Definition 11 (Preference Pattern) $N\left(d\right)$ is a preference pattern on $d\subseteq W$ iff $N\left(d\right)$ is a reflexive and transitive relation on $d$.

A non-trivial normative preference pattern $N\left(d\right)$ on $d$ systematically encodes the accepted normative rules relevant to $d$. The accepted normative rules relevant to $d$ gives a set of propositions that determines the preference ranking over possible worlds in $d$ like an ordering source $g$ does in ordering semantics. The set of relevant normative rules to $d$ includes all normative rules regarding the supersets of $d$. Consider a normative preference pattern $N\left(〚\varphi 〛\right)$ on $〚\varphi 〛$ which is determined by the set of accepted normative rules relevant to situations where $\varphi$ holds. The set of normative rules that are relevant to the situation where $\varphi$ holds are: ${\mathbf{O}}_R({\psi }_1/\chi )$, ${\mathbf{O}}_R({\psi }_2/\chi )$, …, ${\mathbf{O}}_R({\psi }_n/\chi )$ for any $\chi$ such that $〚\chi 〛\supseteq 〚\varphi 〛$. For example, both Sue’s moral duty not to lie and her conditional obligation to apologize if she breaks a promise are the relevant normative rules to the situation where she breaks her promise.

Definition 12 (Normative Preference Pattern on $〚\varphi 〛$) For $\chi$ such that $〚\chi 〛\supseteq 〚\varphi 〛$, ${\mathbf{O}}_R({\psi }_1/\chi )$, ${\mathbf{O}}_R({\psi }_2/\chi )$, …, ${\mathbf{O}}_R({\psi }_n/\chi )$ are the normative rules applied to $\varphi$ -situations. Let $P_{\varphi }$ be the set of all propositions that are expected to be fulfilled given the normative rules relevant to $\varphi$-situations: $P_{\varphi }=\{{\psi }_1,{\psi }_2,\dots {\psi }_n\}$.

$N\left(〚\varphi 〛\right)=\left\{〈w,v〉\right\}$ for $w,v\in 〚\varphi 〛$, every proposition in $P_{\varphi }$ that holds in $v$ also holds in $w$}

A preference pattern $N\left(d\right)$ is defined by a set of pairs of possible words; when $〈w,v〉\in N\left(d\right)$, let’s write $w{\underset{\_}{\prec }}_{N\left(d\right)}v$. It reads: $w$ fulfills as many relevant normative rules as $v$ does.

Definition 13 (Structured Information State $\mathbf{\sigma }$) $\sigma$ is a structured information state defined by a pair of a frame $N$ and a set of possible worlds, $s\subseteq W$: $\sigma =〈N,s〉$.

1. An information state $\sigma =〈N,s〉$ is coherent, where $s$ is a non-empty subset set of $W$ and $N$ is a coherent frame on $W$;

2. The minimal state $\mathbf{0}=〈N_0,W〉$, where $N_0\left(d\right)=\left\{〈w,v〉|w,v\in d\right\}$ for every $d\subseteq W$;

3. The absurd state $\mathbf{1}=〈N_1,Ø〉$, where $N_1\left(d\right)=\left\{〈w,w〉|w\in d\right\}$ for every $d\subseteq W$.²⁰

Interestingly, the notion of a structured information state in my update semantics is comparable to the way that ordering semantics uses two contextual parameters. In this system, an information state $\sigma$ is defined by a pair of a preference frame $N$ and a set of accessible possible worlds $s$: $\sigma =〈N,s〉$. $s$ is comparable to $\cap f\left(i\right)$ and the role of a preference frame $N$ is comparable to $g\left(i\right)$ in ordering semantics.

Definition 14 (Refinement of Preference Pattern) Let $N\left(d\right)$ and $N\prime \left(d\right)$ be preference patterns on $d\subseteq W$.

1. $N\prime \left(d\right)$ is a refinement of $N\left(d\right)$ iff $N\prime \left(d\right)\subseteq N\left(d\right)$;

2. $N\left(d\right)\circ 〚p〛$ is a refinement of $N\left(d\right)$ with the proposition $〚p〛$;

   $N\left(d\right)\circ 〚p〛=\left\{〈w,v〉\in N\left(d\right)|\text{if}\hspace{0.17em}v\in 〚p〛,\hspace{0.17em}\text{then}\hspace{0.17em}w\in 〚p〛\right\}$.

The notion of refinement allows us to capture the change in a preference pattern when accepting a normative rule expressed by ${\mathbf{O}}_R(\psi /\varphi )$. Consider, for example, Sue’s moral duty to keep her promise (${\mathbf{O}}_R(p/\top )$) and her conditional moral duty to apologize if she does not keep her promise (${\mathbf{O}}_R(a/\neg p)$). Accepting ${\mathbf{O}}_R(p/\top )$ has the effect of ranking all $p$-worlds over $\neg p$-worlds. Accepting ${\mathbf{O}}_R(a/\neg p)$ has the effect of ranking all -worlds over -worlds. These effects on a preference pattern by accepting normative rules are expressed in terms of the refinements of a preference pattern.

Accepting ${\mathbf{\text{O}}}_R\left(p/\top \right):N\left(W\right)\circ 〚p〛=\left\{〈w,v〉\in N\left(W\right)|\hspace{0.17em}\text{if}\hspace{0.17em}v\in 〚p〛,\hspace{0.17em}w\in 〚p〛\right\}$.

Accepting ${\mathbf{\text{O}}}_R\left(a/\neg p\right):N\left(〚\neg p〛\right)\circ 〚a〛=\left\{〈w,v〉\in N\left(〚\neg p〛\right)|\hspace{0.17em}\text{if}\hspace{0.17em}v\in 〚a〛,\hspace{0.17em}w\in 〚a〛\right\}$.

We can also define the notion of refinement of a frame and its coherence as follows.

Definition 15 (Refinement of Frame) Let $N$, $N\prime$ and $N_{\psi }/\varphi$ be frames on $W$.

1. The frame $N\prime$ is a refinement of $N$ iff $N\prime \left(d\right)\subseteq N\left(d\right)$ for every $d\subseteq W$.

2. The frame $N_{\psi }/\varphi$ is the refinement of $N$ such that for any $d\subseteq W$,

   1. If $d\ne 〚\varphi 〛$, $N_{\psi }/\varphi$ assigns $N\left(d\right)$ to $d$; and

   2. If $d=〚\varphi 〛$, $N_{\psi }/\varphi$ assigns $N\left(〚\varphi 〛\right)\circ 〚\psi 〛$ to $d$.

Definition 16 (Ideal and Optimal Worlds)

1. $w$ is an ideal world in $\sigma =〈N,s〉$, iff $w\in W$ and $w{\preccurlyeq }_{N\left(w\right)}v$ for every $v\in W$.

2. Ideal $\left(〈N,s〉\right)$ is the set of all ideal worlds in $〈N,s〉$.

3. $w$ is a optimal world in $\sigma =〈N,s〉$ iff $w\in s$ and there is no $v\in s$ such that $v{\prec }_{N\left(s\right)}w$.

4. Optimal $\left(〈N,s〉\right)$ is the set of all optimal worlds in $〈N,s〉$.

Definition 17 (Coherence) Let $N$ be a frame on $W$, and $d\subseteq W$.

1. $w$ is a best world in $N\left(d\right)$ iff $w\in d$ and $w{\preccurlyeq }_{N\left(d\right)}v$ for every $v\in d$.

2. Best $\left(N\right(d\left)\right)$ is the set of all best worlds in $N\left(d\right)$.

3. $N$ is coherent iff for every non-empty $d\subseteq W$, Best $\left(N\left(d\right)\right)\ne \varnothing$.

Using these new devices now we can define the dynamic meanings of sentences in $L_2^{\mathcal{A}}$.

Definition 18 (Update Function for Structured Information States) Any sentence $\chi$ of $L_2^{\mathcal{A}}$ is such that $\chi =\varphi ;={\mathbf{O}}_R(\psi /\varphi );$ or $={\mathbf{O}}_J(\psi /\varphi )$ for $\varphi$ and $\psi$ in $L_0^{\mathcal{A}}$. For every sentence $\chi$ of $L_2^{\mathcal{A}}$ and an information state $\sigma =〈N,s〉$, $\sigma \left[\chi \right]$ is determined as follows:

1. If $\chi =\varphi$, then $\sigma \left(\chi \right)=〈N,s\left[\chi \right]〉$, provided that $s\left[\chi \right]\ne \varnothing$.

2. If $\chi ={\mathbf{O}}_R(\psi /\varphi )$, then $\sigma \left[\chi \right]=〈N_{\psi /\varphi },s〉$, where $N_{\psi }/\varphi$ is coherent and $〚\varphi 〛\cap 〚\psi 〛\ne \varnothing$; $\mathbf{1}$, otherwise.²¹

3. If $\chi ={\mathbf{O}}_J(\psi /\varphi )$, then $\sigma \left[\chi \right]=\{\begin{array}{ll}\sigma ,\hfill & \text{if}\hspace{0.17em}\mathit{Optimal}\left(〈N,s\left[\varphi \right]〉\right)\subseteq 〚\psi 〛;\hfill \\ \text{1},\hfill & \text{otherwise}\hfill \end{array}$

Note that updating $\sigma =〈N,s〉$ with ${\mathbf{O}}_R(\psi /\varphi )$ amounts to refining the frame $N$. Updating $\sigma$ with ${\mathbf{O}}_J(\psi /\varphi )$ amounts to testing whether the optimal worlds (most preferred worlds) in $s\left[\varphi \right]$ given $N\left(s\right)$ are $\psi$-worlds. The update semantics is designed to capture an information state $\sigma$ changes when an agent in an information state $\sigma$ accepts $\varphi$. If $\sigma \left[\varphi \right]\ne \mathbf{1}$, then $\varphi$ is acceptable in $\sigma$; if $\sigma \left[\varphi \right]=\mathbf{1}$, then $\varphi$ is not acceptable in $\sigma$. Likewise, a normative rule ${\mathbf{O}}_R(\psi /\chi )$ is acceptable only when the resulting refinement of a frame $N$ is coherent.²²

If an agent is in the information state $\sigma \left[{\mathbf{O}}_J\right(q/p\left)\right]=\sigma$, it is adequate for the agent to accept or make the normative judgment that it ought to be the case that $q$ if $p\left({\mathbf{O}}_J\right(q/p)$). If an agent is in the information state $\sigma \left[{\mathbf{O}}_R\right(q/p\left)\right]=\sigma$, it is adequate for the agent to accept or utter a normative rule can be expressed by ${\mathbf{O}}_R(q/p)$.

Acceptance, Consequence and Consistency for a structured information state $\sigma$ are defined similarly as before.

Definition 19 (Acceptance/Support)

Definition 20 (Dynamic Consequence)

${\varphi }_1,{\varphi }_2,\dots ,{\varphi }_n\models \psi$ iff $\forall \sigma \in \Sigma$: if $\sigma \left[{\varphi }_1\right]\left[{\varphi }_2\right]\dots \left[{\varphi }_n\right]=\sigma$, then $\sigma \left[\psi \right]=\sigma$.

Definition 21 (Consistency)

A sequence of sentences, ${\varphi }_1,\dots ,{\varphi }_n$ is consistent iff $\exists \sigma :\sigma \left[{\varphi }_1\right]\dots \left[{\varphi }_{\mathrm{n}}\right]\ne \mathbf{1}$.

This updated semantics for normative reasoning licenses the the characteristic inferences in normative reasoning (n1)–(n5). This can be shown as follows using acceptance: (n1*)–(n5*).

These inferences show that acceptance is non-monotonic with normative and factual judgments, while normative rules are not sensitive to propositional updates.

The proposed update semantics validates some versions of Factual Detachment and Deontic Detachment for a coherent information state σ that allow us to infer new normative judgments, while new normative rules are not derived from either detachment rules.

Factual Detachment

Deontic Detachment

Agglomeration does not generally hold, but a conjunction of normative judgments is inferable in limited occasions.

Agglomeration

The two kinds of $\mathit{ought}$s in this update semantics for normative reasoning play a critical role in explaining conflicting intuitions about normative inferences. There is no general inference pattern in normative reasoning that allows us to derive new normative rules, while Factual Detachment, Deontic Detachment, and Limited Agglomeration allow us to infer new normative judgments. This result makes sense because an agent can infer what she practically ought to do from a given set of accepted normative rules and what is known, but an agent does not acquire new rules from what is already known to or accepted by her.

So far I have sketched a simple version of the update semantics for normative reasoning.²³ There are some details left to be filled in, but the basic picture of this dynamic approach must be clear enough to illustrate the intuitive and natural distinction between normative rules and normative judgments and solve the CTD Trilemma.

6.5. A Dynamic Solution to the CTD Trilemma

Let’s see how the update semantics for normative reasoning handles Chisholm’s example and solves the CTD Trilemma. We have seen that Jones’s predicament in the CTD Situation is most naturally illustrated by the following five statements.

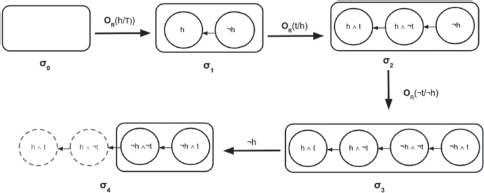
In the update semantics for normative reasoning, accepting the normative rules (c1)–(c3) and the factual statement (c4) in the Chisholm set brings about the changes illustrated in the following diagram.

In this diagram, ${\sigma }_0$ is the minimal state $\mathbf{\text{0}}=〈N_0,W〉$. ${\sigma }_4$ is the resulting information state of updating (c1)–(c4) in the CTD situation:

The resulting information state ${\sigma }_4$ supports not only (c1)–(c4), but also (c5) ${\mathbf{O}}_J(\neg t)$. ${\sigma }_4\left[{\mathbf{O}}_J\right(\neg t\left)\right]={\sigma }_4$ since $\mathit{Optimal}\left({\sigma }_4\right)\subseteq 〚\neg t〛$.²⁴ However, (c6) ${\mathbf{O}}_J\left(t\right)$, (c7) ${\mathbf{O}}_J(h\wedge \neg t)$ and (c8) ${\mathbf{O}}_J(t\wedge \neg t)$ are not supported by ${\sigma }_4$. For ${\sigma }_4=〈N,s〉$, $\mathit{Optimal}(〈N,s〉)\cancel{\subseteq }〚t〛,\cancel{\subseteq }〚h\wedge \neg t〛$ and $\cancel{\subseteq }〚t\wedge \neg t〛$.