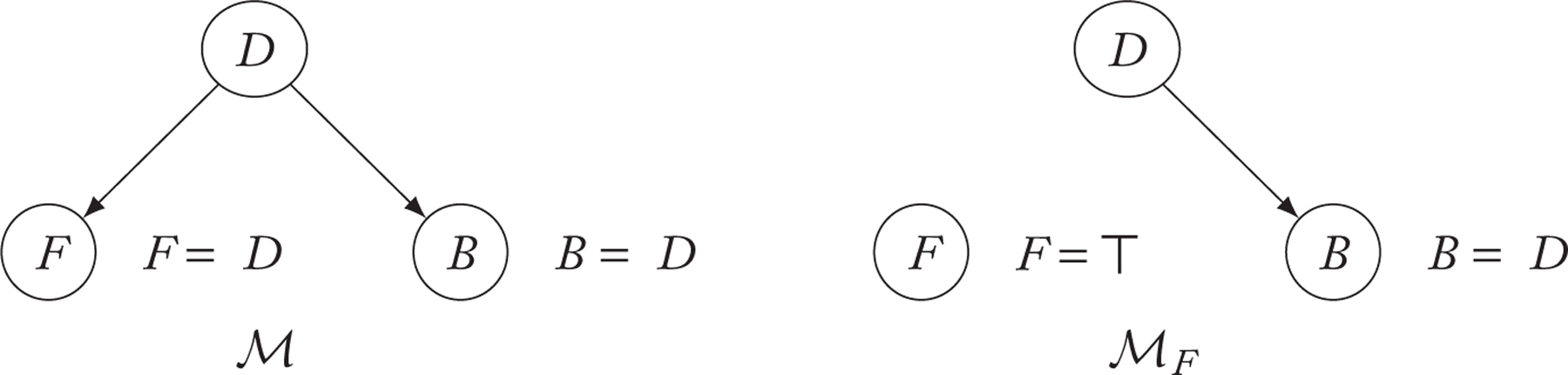1. Overview
Those with an interest in the topic will concur that special rules apply when reasoning from a counterfactual hypothesis. Statements that are not so closely tied to the way things happen to be would appear to tell us more, by a kind of accommodation, about the way things generally go.1 The apparently non-epistemic nature of counterfactual modality has, moreover, spurred philosophers in their search for objective (or “metaphysical”) underpinnings of necessity and possibility (e.g., Kment 2014; Williamson 2007).
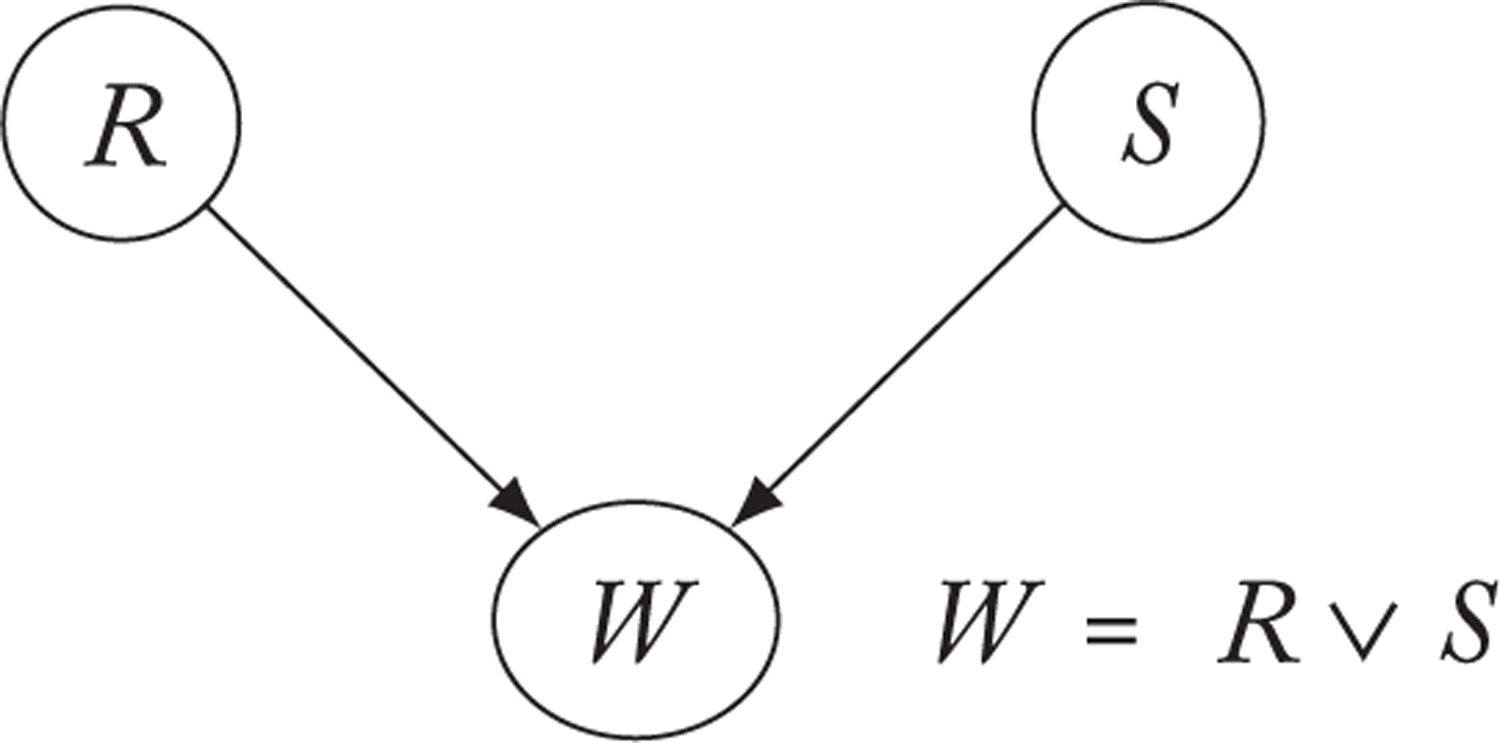
Logical and metaphysical theses about counterfactuality invariably draw on linguistic evidence concerning the use of the counterfactual conditional sentence. Some of the characteristic features of counterfactual reasoning and modality can be extracted, it is thought, from a side-by-side comparison with a contrasting indicative form (cf. Adams 1970):2
| (1) | a. | If Pennie is at that bus stop, she is wearing a hat. |
| b. | If Pennie were at that bus stop, she would be wearing a hat. (Humberstone 2011: 927) |
But there is a further difference between the two, which will concern us here. Observe that the conditionals in (1) are, in a sense, enthymematic. Both require supplementation by further facts about the situation to complete the argument from antecedent to consequent. As it turns out, this factual supplementation is restricted, in a particular way, for (1b). There is no similar restriction on (1a).5
The indicative conditional (1a) would be a natural utterance for one who, surveying the bus stop, saw that everyone there was wearing a hat. Yet the same observation cannot bridge the gap in the counterfactual conditional (1b). Instead, one would need to know, for instance, that it was Pennie’s custom to put on a hat when venturing outside. While the first supplementary fact is a correlation that could well be random (“the way things happen to be”), the second is a more robust behavioural trait (“the way things tend to go”). As an initial pass, then, (1b) is restricted to supplementation by generalizations of the more robust sort.
Theorists have assumed the restriction on (1b) is general to all counterfactual conditionals, and is attributable specifically to (1b)’s counterfactuality.6 Indeed, the following theoretical views are commonplace, or at least prominently represented, in the literature:7
Indicative conditionals, such as (1a), are epistemic modals (ranging over worlds that are epistemically possible).
Counterfactual conditionals, such as (1b), are, by contrast, metaphysical modals (ranging over worlds that are metaphysically possible).
Indicative conditionals are evaluated by reasoning from a knowledge base that may contain highly contingent facts.
Counterfactual conditionals are evaluated by (hypothetically) changing the world in a certain respect and determining what other changes follow from that one by general laws.
These views, when properly spelled out, are able to predict the pattern just instanced: (1b) must be supplemented by something resembling a general law of hat-wearing, while it is okay to link the clauses of (1a) by a non-lawlike generalization that happens to hold.
In this paper, we challenge the initial claim that the restriction on (1b) is characteristic of all and only counterfactuals, and hence the general assumption that the linguistic evidence in (1) bears on counterfactuality per se. As we will see, the same restriction occurs on certain modals that would be classified as epistemic and whose prejacents are inferred to hold in actuality. One such modal is (a particular use of) the English auxiliary will. This modal—the subject of Winans (2016)—is of particular interest, since it is the present tense counterpart of would, the auxiliary occurring in the consequent of (1b) (cf. Dudman 2001: 122–23).
To demonstrate the same restriction for will, we return to the case of Pennie and the bus stop. Like the indicative conditional (1a), sentence (2a) is appropriate in a context where we can see that everyone at the bus stop is wearing a hat, and we know that, although we haven’t spotted her yet, Pennie is among them. But in the same circumstances, (2b) is not appropriate. It improves if, instead of deriving the conclusion from what is visible at the bus stop, the speaker knows that Pennie wears a hat by habit.
| (2) | a. | Pennie must be wearing a hat. |
| b. | Pennie will be wearing a hat. |
This parallel between (2b) and (1b), and the fact that they contain related modal auxiliaries, convinces us that, in the case of (1b), the restriction is due to the choice of auxiliary in the consequent, rather than its counterfactuality. Indeed, we are attracted by the following suite of claims:
will and would apply the same constraint to their prejacent, namely anti-abductivity (to be introduced in §2).
The anti-abductivity common to will and would is responsible for the relevant difference between (1a) and (1b), and many similar pairs that have led theorists to assign a distinctive status to counterfactuals.
Just as there are alternatives to will that are not anti-abductive (e.g., must), so are there alternatives to would in the consequent of a counterfactual conditional that are not anti-abductive, including (in English) the auxiliary cluster ‘would have (to)’.
The abductive/anti-abductive distinction does not pertain to the source of supplementary premises (i.e., the Kratzerian modal base and ordering source), and consequently should not be taken as a distinction in modality, along the lines of the epistemic/deontic distinction. It is instead a (fine-grained) difference in evidential status, more like the inferential/testimonial distinction.
We begin the argument in the next section with a detailed discussion of anti-abductivity in inferential will based on Winans (2016). Following that we show that will’s anti-abductive constraint also fits counterfactuals with would in the consequent.
2. Introducing Anti-Abductivity
The English auxiliary will, familiarly, marks the future. But it has a second use as an inferential modal, where its occurrence is consistent with a present temporal interpretation of the embedded clause. The second use is clearly in force when that clause is stative and modified by now, as in ‘Alma will be home now’.8
Inferential will is a necessity modal, similar to must.9 Necessity modals, according to a prominent line of analysis, are operators that claim their prejacent (i.e., operand) follows from a particular set of premises.10 Observe that neither ‘will ’ nor ‘must ’ is felicitous when is established “directly” by the senses:
| (3) | Watching rain fall from the sky. | |
| a. | #It must be raining. (Karttunen 1972) | |
| b. | #It will be raining (now). (Winans 2016: 19) | |
An abduction, for our purposes, is an inference from a proposition to its explanation or cause.13 It may include further premises that are not themselves explained by its conclusion (e.g., the negation of a competing explanation), and the explanation in question may only be partial. But if there is partial explanation of at least one premise by the conclusion of an inference, that inference qualifies as an abduction. Here is a simple illustration:
| (4) | Angela knows that her neighbors barbecue often. A friend is over at her house and they both smell smoke. Angela says: | |
| a. | The neighbors must be barbecuing. | |
| b. | #The neighbors will be barbecuing (now). (Winans 2016: 1) | |
If the inference goes from cause to effect instead, will is felicitous:
| (5) | Angela and Matt know that their neighbors barbecue every Friday night. While away from home, Angela realizes it’s Friday night. She says to Matt: | |
| a. | ?The neighbors must be barbecuing. | |
| b. | The neighbors will be barbecuing (now). (Winans 2016: 2) | |
Note the explanatory relationship does not have to be causal for the inference to be an abduction:15
| (6) | An inventory of the coins that have fallen down the back of the sofa reveals (to me) that all are silver. My son says he lost his favourite coin back there. I say: | |
| a. | It must be silver. | |
| b. | #It will be silver. | |
The inference is an abduction because the premise (‘every coin down the back of the sofa is silver’) is partially explained by the prejacent (‘ is silver’, where names my son’s favourite coin). We assume that accidental generalizations like this one metaphysically depend on the status of the individuals they generalize over (cf. Rosen 2010: 120). Thus whether every coin down the back of the sofa is silver depends (where , and are the only coins down the back of the sofa) on whether is silver, whether is silver, and whether is silver. The dependency is not, however, causal: those facts do not cause every coin to be silver.
A law or nonaccidental generalization, by contrast, serves to (partially) explain the individual cases falling under it (Rosen 2010: 119–20; cf. Kratzer 2012: 122–23, 138–39). That’s why (5b) sounds good, though the prejacent is an instance of the generalization that occurs as a premise (the neighbours barbecue every Friday night). Moreover, if we replace the generalization in (6) with one that is nonaccidental, will is fine again:
| (7) | Being an avid birder, I know that all the swans in this part of the world are black. You tell me that a swan has built a nest in the attic. I say: | |
| a. | ??It must be black. | |
| b. | It will be black. | |
In her dissertation, Winans looks at a range of further examples in English, and also extends her investigation to other languages. The pattern just described turns out to be cross-linguistically robust: the counterparts of inferential will in other languages (i.e., modals that have an alternative use marking the future) are anti-abductive too.16
Before moving on, we make one last point about will. Blocking abduction and requiring exclusively forward inference are not the same thing. There are inferences that are not abductions by our earlier definition, but that contain one or more abductive (or backward) steps:
| (8) | Angela knows that her neighbors barbecue often, and that when they have barbecues they get drunk. A friend is over at her house and they both smell smoke. Angela says: | |
| a. | The neighbors will be drunk (now). (Winans 2016: 33) | |
The inference supporting (8a) proceeds from one effect (the smoke) to another (the drunkenness) via their common cause (the barbecue). While the first step is abductive, the argument as a whole is not (the smoke is explained by the barbecue, but not by the drunkenness). The fact that (8a) is felicitous indicates that will’s restriction targets abduction specifically, not just any inference containing an abductive step.17
3. Counterfactuals
Our aim here is to argue that the linguistic behaviour supposed to be distinctive of counterfactuals is instead a manifestation of the anti-abductivity contributed by a modal auxiliary. In the previous section, we used the non-counterfactual modal will to illustrate anti-abductivity. In this one, we find the same constraint on would-counterfactuals,18 and show that it accounts for the judgments at the beginning of the paper.
3.1. Inferential Analysis
An early account (Chisholm 1946) of the meaning of counterfactual conditionals treats them as claims that the proposition, , contributed by the consequent,19 follows from the proposition, , contributed by the antecedent, in conjunction with a body of supplementary facts, .
| (9) | is true iff | |
| a. | is true | |
| b. | follows from | |
In other words, the bare counterfactual conditional compresses a specific piece of reasoning that may rely on additional (factual) premises and contain intermediate steps.20
This inferential analysis makes the comparison with inferential will from the previous section straightforward, and for that reason we take it as our starting point. Though the “similarity” semantics of Stalnaker and Lewis is more popular, the inferential approach is largely intertranslatable with it,21 and the added complexity of the Stalnaker-Lewis model does not in this case confer any benefits.
The relevant body of supplementary facts, , is left unspecified in (9). This may be seen as an attractive feature. Suppose it is Alma’s birthday. She’s turning 40, and the year is 2020. It seems that either counterfactual below is acceptable in the context:
| (10) | a. | If Alma had been born in the year 2000, she would be turning 20. |
| b. | If Alma had been born in the year 2000, it would now be 2040. |
It is possible to spell out the supplementary factual premises in the surrounding linguistic context. One way is to present the counterfactual as the conclusion of an argument:23
| (11) | It is now 2020, so | ||
| a. | If Alma had been born in 2000, she would be turning 20. [True] | ||
| b. | If Alma had been born in 2000, it would now be 2040. [False/#] | ||
| (12) | Alma is turning 40, so | ||
| a. | If she had been born in 2000, she would be turning 20. [False/#] | ||
| b. | If she had been born in 2000, it would now be 2040. [True] | ||
3.2. Anti-Abductivity in Would-Counterfactuals
As Goodman (1947) famously pointed out, there are cases where follows from and certain facts (and is contrary to fact) yet the would-counterfactual is either false or infelicitous. Though this wasn’t yet apparent to Goodman, the cases turn out to be those where is a cause or explanation either of or a member of . The excluded inferences are abductions (Bjorndahl and Snider 2015).
Here’s an example similar to Goodman’s. Suppose the lawn is wet and the only possible explanations are inclement weather or the sprinkler (which, it is important to note, operates on a timer and so is independent of the weather). In the event that the sprinkler has been off and rain is responsible for the wet lawn, we get the following judgments:
| (13) | If it hadn’t rained, the grass would be dry. [True] |
| (14) | If it hadn’t rained, the sprinkler would have been on. [False/#] |
From the counterfactual hypothesis (it hasn’t rained), supplemented by the fact that the sprinkler was off, we can derive the consequent of (13): the grass is dry. But note that from the same hypothesis, supplemented instead by the fact that the grass is wet, we can also derive the consequent of (14): the sprinkler was on.25 The basic inferential analysis (9) therefore predicts that either conditional, with the right supplementation, will be true. But this prediction is incorrect: (14) cannot be heard as true. Indeed, if we try to make the supplementary premise explicit, the result sounds incoherent:
| (15) | #If it hadn’t rained, the sprinkler would have been on, since the grass is wet. |
The problem seems to be that the inference supporting the consequent of (14) is abductive: the conclusion (the sprinkler was on) provides the explanation for one of the premises (the grass is wet). This is not so for (13), where the inference runs from cause (no rain and no sprinkler) to effect (dry grass). In further support of this diagnosis, observe that (14) out of the blue suggests a mechanism that turns the sprinkler on after a dry spell. Left to fill in the details ourselves, we default to a non-abductive argument.
Anti-abductivity in would-counterfactuals parallels the case of inferential will, already discussed. Abduction to the consequent of the counterfactual is blocked—which is to say, to the prejacent of would. And would, of course, is the past tense of will. One is tempted, therefore, to see woll, the lexeme common to will and would (Abusch 1997: fn. 14), as the source of anti-abductivity in both cases.26 There is correspondingly little temptation to attribute the constraint on would-counterfactuals to their counterfactual marking (such an account would not extend to will). An upshot of this is that the linguistic argument for the distinctive nature of counterfactual reasoning and modality is seriously compromised.
For if we return to Humberstone’s contrasting pairs of conditionals, meant to exemplify the difference between indicative and counterfactual, we find that anti-abductivity (in the (b) sentences) is sufficient to explain the relevant contrast.27
| (16) | a. | If Pennie is at that bus stop, she is wearing a hat. |
| b. | If Pennie were at that bus stop, she would be wearing a hat. | |
| (17) | a. | If there was pepper in the tea, I didn’t taste it. |
| b. | If there had been pepper in the tea, I wouldn’t have tasted it. | |
| (18) | a. | If there is a kitten in this room, it is concealed from view. |
| b. | If there were a kitten in this room, it would be concealed from view. |
The (accidental) generalization that everyone at the bus stop is wearing a hat is explained in part by the proposition that Pennie (who, by hypothesis, is at the stop) is wearing a hat (see (6) above). Thus, if that generalization is used as a premise in the derivation of that proposition, the derivation is an abduction. The same goes for the blocked premises in the remaining two (b) examples. Failing to detect (i.e., not tasting) the pepper that is (by hypothesis) in the tea would explain the absence of that flavour when the tea was sipped; and the kitten in question’s being concealed from view explains the fact that no kitten can now be seen, though one is in the room (by hypothesis).
A serious issue for the view that the (a) and (b) sentences above exemplify the difference between indicative and counterfactual is that the same contrast holds between indicatives: between those that do and those that do not contain (inferential) will—just as our account tracing anti-abductivity to the auxiliary (will/would) predicts (cf. Dudman 1988: 120).
| (19) | a. | If Pennie is at that bus stop, she is wearing a hat. |
| b. | If Pennie is at that bus stop, she will be wearing a hat. | |
| (20) | a. | If there was pepper in the tea, I didn’t taste it. |
| b. | If there was pepper in the tea, I won’t have tasted it. | |
| (21) | a. | If there is a kitten in this room, it is concealed from view. |
| b. | If there is a kitten in this room, it will be concealed from view. |
We take ourselves by now to have made a case for the first two items from our earlier list:
will and would apply the same constraint, namely anti-abductivity.
The anti-abductivity common to will and would is responsible for the relevant difference between (1a) and (1b), and many similar pairs that have led theorists to assign a distinctive status to counterfactuals.
Further support for our account emerges from a consideration of counterfactual conditionals that allow abduction.
3.3. Abductive Counterfactuals
On our account, the anti-abductivity of would-counterfactuals is due to the choice of auxiliary in the consequent (would), rather than their counterfactuality. We are therefore in a position to explain another feature of the linguistic data: the existence of counterfactual conditionals—with a different auxiliary structure in the consequent—that permit abduction.
Consider the following variant of (13):
| (22) | If it hadn’t rained, the sprinkler would have to have been on (since the grass is wet). [True] |
Counterfactual forms29 that permit abduction furnish counterexamples to the hypothesis that reasoning from counterfactual premises is inherently anti-abductive, and hence to the idea that the counterfactuality of (1b) is responsible for this restriction on its use. But while the ‘would have to’ form and its properties have long been observed, and even carefully documented,30 the lesson has been resisted, and the importance of counterfactuality upheld, by various conservative tactics.
Broadly speaking, two lines of resistance are possible: (i) deny that ‘would have to’-counterfactuals are truly abductive, or (ii) deny that they are bona fide counterfactuals. A way to pursue the first approach is to dissect the double auxiliary into an ordinary (i.e., anti-abductive) would-counterfactual and a further embedded necessity claim (viz., that so-and-so has to be the case) in its consequent.31 There are various versions of the second approach; an extreme one is to claim that abductive counterfactuals are only true if reinterpreted as indicatives.32
Schulz (2007: Ch. 5) offers a more nuanced position. She holds that every counterfactual sentence can be interpreted as either an “ontic” (i.e., metaphysical) or an epistemic modal, and while the epistemic reading allows abduction, the ontic does not. Though conceding that not all counterfactuals are anti-abductive, her position is similar to the second line of resistance above, in that abductive conditionals are consigned to a different—and peripheral—modal category. She is, in this way, able to maintain a connection between anti-abductivity and the primary sort of counterfactual modality: ontic/metaphysical.
There is no real evidence for such an ambiguity, however. If all counterfactuals have an epistemic reading, then it should be possible to hear would-counterfactuals with abductive support as true.33 We ought to hear a true reading of (14), and, for that matter, this wonderful example of Arregui’s (2005: 91):
| (23) | A driver stops her car. The bridge she is driving on is unfinished, and a gap yawns ahead. |
| If the driver had kept going, the bridge would have been completed. |
But no true reading can be heard.
We have limited ourselves, in the consideration of counterfactual forms, to an examination of English. Our finding is that, here at least, verbal auxiliaries make up a paradigm in which counterfactuality and anti-abductivity are independently marked (see Table 1).34 Our hunch is that this will turn out to be the rule across languages. As Winans (2016) already showed, there are anti-abductive indicatives (counterparts of will) in other languages. We expect to find abduction-allowing counterfactuals (counterparts of ‘would have to’) in other languages too, even among those with very different ways of marking counterfactuality.35 We are skeptical, then, of any close conceptual connection between anti-abductivity and counterfactuality, and doubt that the one can be derived from the other. It seems to us that permitting a hypothetical premise to be contrary to fact and blocking abductive inferential support are simply different jobs that languages don't need to bundle together.36
Some English Modal Auxiliaries
| Counter-Factual | Anti-Abductive | |
|---|---|---|
| + | − | |
| + | would | would have to |
| − | will | must |
4. Anti-Abductivity in Action
In this section, we use special models of propositional logic to formalize anti-abductivity and offer (pared-down) truth conditions for will, would, and others.37 The models are structural equation models (SEMs), and they make use of structural equations of the form
to express dependencies between propositions.38
For example, suppose as before that the lawn is wet () if it has rained () or the sprinkler has been on (). Here depends on both and , and its truth-value corresponds to that of . This dependency is expressed as follows (with the dependent proposition on the left):
More generally, a (boolean) SEM is a triple
where
is a finite set of boolean variables (i.e., atomic propositions),
is a subset of (the endogenous—or dependent—variables), and
Each is a boolean expression over , such that , where is the set of variables from occurring in .
A truth assignment for an SEM is a function that verifies, for each , the formula .
The -parents of are the atomic propositions occurring in (i.e., atom ).39 In Figure 1, parenthood is indicated by a directed edge. The -ancestor relation is the transitive closure of the -parents relation, and we write for is an -ancestor of (Bjorndahl & Snider 2015: 11).
We can now state the anti-abductivity constraint. We take it to apply to a proposition (the prejacent of the anti-abductive modal auxiliary) in relation to a further set of propositions (the premise set).40 Briefly, anti-abductivity prevents from being the -ancestor of any member of . More fully, since premises can be logically complex, cannot be an -ancestor of any , for any in :41
| (24) | There is no such that |
4.1. Will
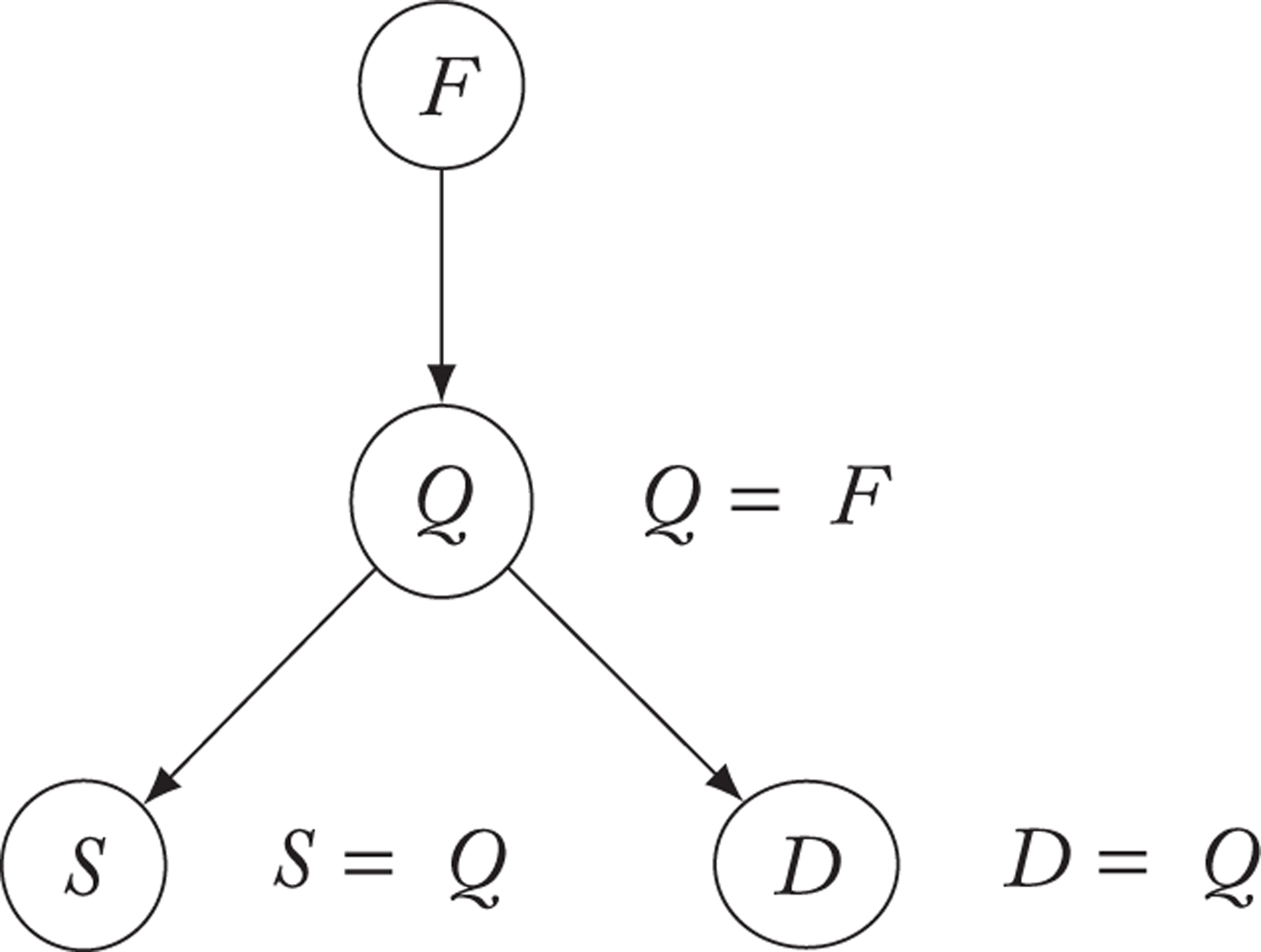
The barbecue scenarios from §2 revolve around the following propositions: it’s Friday night (), the neighbours are barbecuing (), there’s a smoky smell (), the neighbours are drunk (). The dependencies between them are represented in Figure 2.
Given the formulation of anti-abductivity in (24), we correctly predict that (25) is acceptable when its prejacent is inferred from , but not when it is inferred from ; since, as may be read off Figure 2, , .
| (25) | The neighbours will be barbecuing. |
| (26) | The neighbours will be drunk. |
On the other hand, supposing must is not anti-abductive, we predict that (27) is felicitous even if the prejacent is inferred from .
| (27) | The neighbours must be barbecuing. |
We propose the following schematic truth conditions for an utterance of ‘will ’ backed by the premise set :42
| (28) | ‘will ()’ is true in iff | |
| a. | , | |
| b. | ||
| c. | ||
| d. | There is no such that | |
While clause (a) checks that the premises are all true, clause (b) models the indirect evidence requirement by ensuring that is not a trivial consequence of .43 Clause (c) ensures that the prejacent follows once we add the dependencies in .44 Finally, clause (d) is the anti-abductivity constraint. Since we are ignoring anaphoricity,45 the corresponding analysis of ‘must ’ simply drops (d):46
| (29) | ‘must ()’ is true in iff | |
| a. | , | |
| b. | ||
| c. | ||
4.2. Conditionals
On the basic inferential analysis, a conditional is the claim that the consequent follows from the premise set plus the antecedent. We arrive at the following by adding non-triviality and anti-abductivity clauses to that analysis (or, thinking compositionally, by adding the expected contribution of the if-clause to the earlier analysis of ‘will ()’).
| (30) | ‘if , will ()’ is true in iff | |
| a. | , | |
| b. | ||
| c. | ||
| d. | There is no such that | |
Note that only an (un)negated atomic clause can occur as the prejacent of will, so the template above is not a general schema for the conditional.47 The analysis is the same as (28) except that we have replaced ‘’ with ‘’ in clauses (b)–(d).48 Thus, for instance, clause (b) now requires that is not a trivial consequence of augmented by .49 We can get the truth conditions for ‘if , must ()’ by dropping (d), as before.
Counterfactual marking, on our account, relaxes the requirement that is epistemically possible. Since we make no attempt to represent this constraint in (30), the analysis applies unchanged to the schema ‘if , would ()’, and applies minus clause (d) to ‘if , would have to ()’.50
4.3. Adjusting for Error
Structural equation models are limited in two directions. They are limited vertically—they can only go back so far in the causal ancestry of a proposition—and horizontally—a proposition can only have so many parents (i.e., there is a finite limit on the complexity of the function determining its truth-value). In reality, the list of potential factors that immediately bear on a given proposition might be open ended.
Consider the equation we used to model the state of the lawn based on the weather and the sprinkler:
This is an obvious simplification. For one thing, rain doesn’t guarantee a wet lawn. Someone might have parked their car on it (), or even set up a marquee to protect it from the elements ( ). We could add these conditions to the equation, but the result
is not obviously an improvement. The longer formula still fails to capture the true relationship between the variables (the marquee could blow down, the car could leak fluid), and the concession to nuance doesn’t balance the downgrade in elegance.
Since we can’t represent the true situation in a finite formula, we follow Pearl in allocating an additional exogenous error variable to every formula . “Error” is understood to subsume any combination of additional factors (including marquees and the like) that would make the prediction of the original equation come out false.
The introduction of the error variable is not without consequences. For suppose we update the equation as follows51
and then use it to evaluate the counterfactual
| (31) | If it had rained, the grass would be wet. |
Our account now predicts that (31) is only true if the premise set includes the claim that the situation is normal (i.e., ). Without this further premise, we cannot infer from the antecedent . This prediction is not correct.52 For consider that is really the disjunction of every claim to the effect that a particular (inhibiting) error has occurred, and hence spelled out in full is the claim that no marquee has been erected, no car is parked on the lawn, etc. Now suppose someone utters (31) without considering whether a car might be parked on the lawn. We do not judge the utterance false merely because the negation of this unlikely proposition did not occur in their reasoning.53 Indeed, anyone who utters (31) must fail to consider some potential source of error, since sources of error can be invented without limit. The problem is a serious one: no one can utter (31) truly on our account as it stands.
But how should we amend it? Note that (31) is not automatically true either (Stone 1994: 184). Instead, its truth-value depends on the facts. Was a car in fact parked on the lawn or not? If one was, (31) is false; if no car was, and indeed nothing else was there to keep the rain off, then (31) is true.
The situation is different for factors that truly are important or salient. We can fault someone who says
| (32) | It must have rained, since the grass is wet. |
The distinction we are relying on between a relevant factor and an abnormal interference is reflected in the interpretation of weak necessity modals (i.e., should and ought).
| (33) | a. | The grass will/must be wet, since it rained. |
| b. | The grass ought to/should be wet, since it rained. |
We can follow (33b), but not (33a), with ‘but it’s not, because I covered it with a tarp.’ Weak modal claims can be true even if the error term is tripped (Stone 1994: 184). But even weak modals sound false if an important or salient variable is ignored:
| (34) | The grass should be dry, since the sprinkler hasn’t been on. |
We propose a revision, in light of the above, to clause (c) in our analysis of inferential modals. For strong modals, the prejacent is required to follow from the premise set along with the actual value of every error variable (for endogenous ). We update (30) accordingly:
| (35) | If , will ()’ is true in iff | |
| a. | , | |
| b. | ||
| c. | ||
| d. | There is no such that | |
Weak necessity modals, by contrast, are true if the inference goes through on the assumption that no error has occurred (whether or not that assumption is correct). They therefore receive the analysis below:55
| (36) | ‘should/ought ()’ is true in iff | |
| a. | , | |
| b. | ||
| c. | ||
| d. | There is no -() such that | |
5. Alternatives to Anti-Abductivity
In this paper we have argued for a reconsideration of linguistic data previously used to support a substantial distinction in status for counterfactuals. The argument, where it is novel, rests on an analogy between (counterfactual) would and (inferential) will. We claim that both forms of woll are anti-abductive, and in §3.2 showed that anti-abductivity in would suffices to explain the linguistic data in question. What we have not yet done is consider alternatives to the anti-abductivity analysis of would-counterfactuals. If there is a better analysis of would-counterfactuals to be had—on which they don’t line up with anti-abductive will—then the analogy, and our argument, does not go through.
5.1. Interventionism
Interventionism (Pearl 1996; 2009) is a precise proposal about the semantics of counterfactuals with widespread currency in contemporary philosophical accounts of modality and psychological accounts of reasoning.56 It shares with Bjorndahl and Snider’s (2015) anti-abductivity analysis the idea that the direction of explanatory dependency is crucial to the truth conditions of (would-) counterfactuals. However, the interventionist, not content with stipulating an embargo on abduction, provides a conceptual rationale against it—one that aligns counterfactual reasoning with experimental intervention.
Performing an experiment is a way of distinguishing causation from correlation. The experimenter brings about a certain state by intervening in the (normal) causal order and disrupting the relationship with that state’s (normal) causal antecedents. (For example, an experimental proband is selected at random to avoid the confounds of self-selection.) The causal consequences of the intervened-on state follow in the usual way, but intervention isolates these from the state’s usual causal ancestors, along with any other state that in the normal course of things it would be (merely) correlated with. In other words, while causal consequences may be inferred from an intervened-on state, other standard inferences, including—but not limited to—abduction to a causal ancestor, are blocked. If you intervene to make the lawn dry (with a blow dryer, say), you cannot turn around and claim that the weather must have been fine.
The anti-abductivity of would-counterfactuals can, therefore, be seen as the surface ripple of something deeper: reasoning based on (hypothetical) intervention. Interventionist protocol both constrains reasoning—in a manner that counterfactuals are supposed to emulate—and gets at what is really there: the underlying causal structure. By comparison, reasoning from what one has “passively” observed is unconstrained (abduction, for instance, is legitimate). But this is so precisely because the objective causal relationships have not been sorted from the myriad other sources of correlation—let alone from the “strange combinations of rare eventualities … that have nothing to do with general traits of influence and behavior” (Balke and Pearl 1994: 231).
Corresponding to the interventionist mode of reasoning is a modality structured by objective features of the world: necessity in virtue of causal and other forms of metaphysical dependency.57 In assigning a profounder origin to the anti-abductivity of would-counterfactuals, interventionism also lends support to the objective (or metaphysical) characterization of their modality—in line with the received view that counterfactuals diverge from the epistemic modality of indicatives.
Interventionism, then, is a formidable alternative to the basic anti-abductivity account we have assumed; one that, moreover, supports the traditional view of the modal difference between counterfactuals and indicatives. We reject it, however, because it fails to provide an accurate characterization of the truth conditions of would-counterfactuals.58
By lumping abduction in with the other inference patterns blocked by intervention, the interventionist ascribes a stronger constraint to (would-) counterfactuals than neat anti-abductivity. This is clear from the following informal first pass at the interventionist truth condition (Cf. Gibbard & Harper 1978; Pollock 1976: 42):
| (37) | is true iff either | |
| a. | , when combined with the facts that do not depend on whether , is sufficient to bring about B, or | |
| b. | is true and does not depend on whether . | |
Route (a) requires the consequent to occur downstream (dependency-wise) of the antecedent and any supplementary factual premises (this is the intended sense of “bringing about”).59 This is a stronger requirement than anti-abductivity, which only says that the path to the consequent must not be upstream of any premise. This discrepancy will become important shortly.
The interventionist algorithm derives the truth condition above by an imagined procedure. We first wind the causal-explanatory history back, undoing everything that depends on the truth-value of the antecedent, . Holding fixed the resulting causal-explanatory background (captured by the actual truth-values of the exogenous variables), we intervene on , setting its value at “true.” The intervention is modelled by detaching from its parents, so that its value can only propagate forward in the graph. Finally, we let a new history “play out” from the same causal-explanatory background—but now with set to true—and see whether the truth of the consequent follows.
This computation is defined below. In the following, is the model identical to except that , while means that matches except possibly in the assignment it makes to endogenous variables.
| (38) | is true in iff | |
| a. | There is a truth assignment for , such that | |
| b. | ||
| c. | ||
With the truth condition now in hand, we can present a counterexample to interventionism. We first observe that, intuitively speaking, a would-counterfactual may be judged true though follows from by an inference that goes by way of a common cause. This holds in the case below, where we infer the bang from the flash via a (counterfactual) detonation (Hiddleston 2005):
| (39) |
A firework fails to detonate. If there had been a flash, there would have been a bang. [True] |
Now a common cause inference is not an abduction , but it is not a purely forward inference either . It consists of a step back (to a causal ancestor) followed by a step forward (to another effect of the same cause). As such, it lands in the gap between the weaker anti-abductive constraint and the stronger interventionist one. While anti-abductivity predicts that (39) is true, interventionism predicts—incorrectly—that it is false. Intervening to make it the case that there was a flash deletes the connection to the parent node representing the detonation of the firework. This blocks any inference from the truth of the former that runs via the truth of the latter (see Figure 3).60
So far in this paper we have avoided the term backtracking. The term was introduced (into the counterfactuals literature) to describe an inference that first went “backwards” and then “forwards.” Thus ‘backtracking counterfactual’ originally meant one that was true in virtue of a common cause inference (as Bennett [2003: 208] chronicles, this meaning was lost, and ‘backtracking’ came to mean simply ‘backwards’ or abductive). The original sense (or at least the underlying concept) merits a revival. As we have seen, it delineates a kind of counterexample to interventionism, and hence an important contour to the empirical landscape.61 ‘Backtracking’ should not be merged with ‘backwards’, precisely because the former is acceptable in would-counterfactuals (and with inferential will, §2), while the latter—abduction—is not (cf. Arregui 2005: 84–85; Bjorndahl & Snider 2005: 7–9).62
5.2. Noncausal Approaches
Anti-abductivity provides an account of would-counterfactuals that is empirically superior to interventionism and related accounts from the causal modelling literature. But how does it compare to quite different approaches that distinguish good and bad examples of would-counterfactuals without restricting the causal direction of the inference? Kratzer 2012 and Ippolito 2016 are prominent accounts in this vein, and useful to consider, though their arguments do not in the end cast doubt on the importance of abduction to the understanding of would-counterfactuals.
Ippolito 2016 contains a useful reanalysis of certain examples that seem at first to call for a causal treatment. To begin with, consider Pavel Tichý’s (1976) case:
| (40) | Invariably, if it is raining, Jones wears his hat. If it is not raining, Jones wears his hat at random. Today, it is raining and so Jones is wearing his hat. |
| But even if it had not been raining, Jones would have been wearing his hat. [False] |
| (41) | Every morning, Jones tosses a coin. If it is raining that day, he wears his hat, but if it is not then he only wears his hat if the coin came up heads. Today, the toss comes up heads, it is raining, and Jones is wearing his hat. |
| But even if it had not been raining, Jones would have been wearing his hat. [True] |
This time the inference goes through. Evidently, certain facts—in this case the fact that the coin came up heads—can occur as premises. Indeed, the judgments may be captured by a familiar rule: facts are admitted as long as they don’t depend (causally) on the antecedent (cf. (37a)). Jones’s hat-wearing depends on the weather; the result of a coin toss does not.
A different diagnosis competes with this causal one, however. In the false case (40), the consequent can only be derived from itself or the negation of the antecedent . While both propositions are true in the scenario, admitting either into the premise set (alongside the antecedent ) ensures a trivial derivation of the consequent . By contrast, the true case (41) is one where the consequent follows from a premise (the coin came up heads) that is logically independent of both clauses of the conditional. Both judgments could be explained, therefore, by a restriction to nontrivial inference (Ippolito 2016: 18). This explanation is especially attractive, given that such a restriction is independently motivated by the (indirect) evidential requirement of the modal.63
Note further that in the scenario of (41) the following seems false:
| (42) | If Smith had tossed the coin instead of Jones, it would still have landed heads. [False] |
A causal dependency account like (37) predicts this only if it can be made out that the result of the toss “depends” (in the relevant sense) on the the person who makes it.64 But now consider the following (cf. Ippolito 2016: 4):
| (43) | Smith’s last counter is twelve squares away from home. Jones throws the dice and rolls a double six. |
| If Smith had rolled the dice instead of Jones, he would have been home. [True] |
The causal structure of (43) does not differ appreciably from that of (42), so it is hard to see how a causal theorist would account for the difference. On the nontriviality approach, however, the explanation is clear: while the consequent of (42) directly concerns the result of the toss (something that can only be trivially inferred from the facts of the case),65 (43)’s consequent concerns a further ramification of this result (which may be nontrivially inferred from it).66
As Ippolito is aware, nontriviality cannot account for every case that would seem to turn on causal features of the situation. In particular, it doesn’t suffice for a correct prediction (of falsity) in our central sort of case, exemplified by (14). For here the supplementary premise (the grass is wet) is logically independent of both conclusion (the sprinkler was on) and antecedent (it hasn’t rained).
Instead, for such cases, Ippolito calls upon a recent account by Kratzer (2012). Kratzer, as it happens, is convinced that causation is a red herring in (13)/(14), since she has found an analogous case where the causal direction is reversed (2012: 140). We set this case aside for the time being, and jump directly to her alternative proposal.
Instead of causal direction, Kratzer’s account is based on the asymmetry between situations that confirm a nonaccidental generalization and those that, while not upsetting the generalization, don’t confirm it either. (‘All ravens are black’ is supposed to be confirmed by the sighting of a black raven, but not by the sighting of a non-black thing that is also not a raven; the sighting of a non-black raven would of course falsify the generalization.) Notoriously, what counts as a confirming situation in this milieu depends on the wording of the generalization (‘All ravens are black’ is confirmed differently than the logically equivalent ‘All non-black things are non-ravens’). In particular, Kratzer’s account predicts (2012: 141–43) that if the generalization is worded as ‘whenever , ’ then a confirming situation is one where both and are the case (as opposed to one where and are the case).
Suppose the generalization operative across (13) and (14) is ‘Whenever it doesn’t rain and the sprinkler is off, the grass is dry.’ Hence a case where it doesn’t rain, the sprinkler is off and the grass is dry is a confirming instance of the generalization, while a case where it doesn’t rain, the sprinkler is on, and the grass is wet, is not. According to Kratzer’s (2012: 144) confirming proposition constraint, facts that yield confirming instances of nonaccidental generalizations are preferred when it comes to supplementing the antecedent of a counterfactual. This means that we will supplement the hypothesis that it hasn’t rained with the fact that the sprinkler is off (rather than the fact that the grass is wet), and hence that (13) is true, and (14) false.67
Note that Kratzer’s account makes different predictions to one based on causal asymmetry. We can compare it to such an account by considering a minimal pair of conditionals that differ in causal direction (from antecedent to consequent), but not in their verifying situation.68 Suppose Bob decides whether to go to the office holiday party based solely on whether Alice is going. If she is going, then he stays at home, but if she isn’t going, he goes. This year, Alice stays home, and so Bob goes.
| (44) | If Alice had gone to the party, then Bob would have stayed home. [True] |
| (45) | If Bob had stayed home, then Alice would have gone to the party. [False] |
We judge the first counterfactual true and the second false. On a causal account, this is easily explained: it is because Bob’s doings have no effect on Alice’s actions. Kratzer’s noncausal account, of course, cannot say this. It treats the rule as a causally neutral biconditional: .69 Of course, by this rule, follows from just as much as follows from . Note that no supplementary premises are required for either inference, so Kratzer’s confirming proposition constraint (which constrains the supplementation of a counterfactual antecedent) doesn’t get traction here. But even if the constraint did apply, the verifying situation is the same for both sentences (i.e., one where Alice goes and Bob stays), so no matter the wording of the rule (whether it is ‘Alice goes if and only if Bob stays’, or ‘Alice stays if and only if Bob goes’), no difference in judgment would be predicted.70
5.3. The King
Kratzer (2012: 140) prefers a noncausal account of the difference between examples like (13) and (14) in part because she takes the following case to belong to the same camp (viz., “Goodman’s Puzzle”), and hence to warrant an explanation in kind.
| (46) | Whenever the Royal Bavarian Flag is up and the lights are on at Leoni Castle, the King of Bavaria is home. As it happens, the lights are on, but the flag is down and the king is away. | |
| a. | If the flag had been up, the king would have been home. [True] | |
| b. | If the flag had been up, the lights would have been off. [False] | |
The second disparity is easier to address than the first. We agree that (46b) is supported by a non-abductive inference, but propose that this inference is obscured by a more salient one supporting (46a).72 Note that once a since-clause specifying the appropriate factual premise is added, foregrounding the inference in question, the counterfactual sounds true:
| (47) | If the flag had been up, the lights would have been off, since the king is away. [True] |
Our proposal is similar to Kratzer’s own explanation of the initial falsity judgment for (46b). On her account, the operative generalization privileges a different argument, whose supplementary premise and conclusion are primed by the wording of the rule (see §5.2).73
Our account of (46b) presupposes the (more salient) veracity of (46a). How then are we to account for this judgment? The first thing to note is that the flag and the lights function as a signal of the king’s presence at the castle. Indeed, this is critical to the way Kratzer’s case operates (cf. Schulz 2007: 89–90). If we remove this feature, the judgments revert to the pattern predicted by anti-abductivity:
| (48) | The only person authorized to raise the flag at Leoni castle is the steward. So: | |
| a. | #If the flag had been up, the steward would have been home. | |
| b. | If the flag had been up, the steward would have to have been home. [True] | |
Now it is well known that evidential marking can be sensitive to the distinction between the content of a signal (or report) and the conclusion of an inference.74 For instance, will and must, which we know to be compatible with inference, are both incompatible with reportage. Suppose you are some distance from the library and observe a sign on the door that reads ‘closed’, it would be moderately eccentric to then muse to yourself:75
| (49) | ??The library will be closed. |
This could be because the inference from the sign to the store’s being closed is abductive, but in that case we would expect the sentence to improve with must. However, neither is it quite right to say:
| (50) | ??The library must be closed. |
The appropriate thing to say is just, ‘The library is closed’. What is more, changing the direction of causation doesn’t alter the judgments. Suppose the game ends when the referee blows her whistle (the signal, in this case, is the cause of what it signals). It is odd, once again, to utter either (51a) or (51b) upon hearing the whistle. Only (51c) is acceptable.
| (51) | a. | ??The game will be over. |
| b. | ??The game must be over. | |
| c. | The game is over. |
Note that will is fine if the inference is to other (non-signalled) consequences of the whistle blowing (e.g., ‘Her ears will be ringing’).
Kratzer’s King of Bavaria case would seem to belong to the same category. Suppose you are passing Leoni Castle and you notice the flag and lights (the official signs of the King’s installation there). The first two remarks (directed to yourself, or a blind companion) seem odd by comparison with the third:
| (52) | a. | ??The king will be home. |
| b. | ??The king must be home. | |
| c. | The king is home. |
Note that (52a) is improved if the king’s presence is inferred instead from the fact that today is the national holiday that he traditionally spends at the castle.
What we propose, then, is that the justification for the prejacent of would as it occurs in (46a) is not inferential, but testimonial. It is the “report” made by the flag and the lights, rather than an inference to their likely cause, that secures the connection between antecedent and consequent. Of course, for this approach to predict the judgment that (46a) is good, it must be that would is compatible with reported prejacents. But this seems to be so, based on other judgments:76
| (53) | a. | If there had been a ‘closed’ sign on the door, the library would have been closed. [True] |
| b. | If the referee had blown her whistle, the game would have been over. [True] |
Note that the judgment in (53a) is surprising if the connection is inferential rather than reportative, since the inference in question is abductive. (Why is there a ‘closed’ sign on the door? Because the store is closed.)
Up to this point in the paper, we have dwelt on analogies between would and will. But here at the end we suggest a difference: will is anti-reportative, while would is not. Hopefully it is clear that this proposal is open to us; the mere fact that will and would share morphology does not mean they must restrict evidence in exactly the same way. Indeed, there is reason to expect just this difference. While there is an alternative to will (and must)—the (reportative) simple clause—in the non-counterfactual paradigm, there is no similar option in the consequent of a counterfactual.77 As a result, if testimonial justifications belong in counterfactual structures, the task of admitting them will fall to a modal auxiliary, and would is a natural choice.
6. Conclusion
We have argued that the actual difference between counterfactuals and indicatives is the relatively mild one of marking whether the antecedent may be assumed false. The greater alleged differences are due instead to the presence of the anti-abductive modal auxiliary would, and reappear in indicative counterparts with will.
We are not the first to argue that would-counterfactuals and will-conditionals belong together (Bennett 2003: 13–15; Dudman 1988; 2001). But those earlier claimants have not clearly distinguished the two senses of will, and so have not based the comparison on its inferential meaning.78 Nor have they pursued the ramifications of this co-classification along the lines we do here.79 In particular, it has not been previously observed that the common constraint is anti-abductivity.80 Hence it has not been argued, on that basis, that anti-abductivity and counterfactuality are dissociable in English. Previous co-classification accounts, lacking these attainments, have failed to draw sustained support (Bennett 2003: 15).
We believe that anti-abductivity is most naturally understood as a refinement of the inferential evidential restriction (Winans 2016: 39), rather than indicating a sui generis modal category. Framing would as an inferential evidential provides independent motivation for the nontriviality constraint argued for by Ippolito (§5.2), and evidential categories have also helped us develop a response to Kratzer’s puzzling example (§5.3). But above all, there is, as far as we can see, no a priori reason to style an abductive modal epistemic and an anti-abductive one metaphysical (pace Schulz 2007: 127). We don’t see abduction as particularly subjective or information-sensitive, nor do we associate forward inference with objectivity. The interventionist metaphor was supposed to push us in that direction, but its rhetorical force waned with interventionism’s empirical credentials.
If we are correct in our main point, the consequences could be far reaching. Since the middle of the last century, it has been assumed that the difference between conditionals (1a) and (1b) is representative of the difference between counterfactual and indicative—between reasoning about what is and what might otherwise have been. Significant texts about the nature of modality and modal reasoning have been written under that assumption, and it remains to be seen what we can still make of them in its absence.
Acknowledgements
We thank the referees and editorial team at Ergo for their care and good advice. Copious thanks also to Will Starr, Gabe Greenberg, Nathan Klinedinst, and Jessica Rett.
Notes
- In particular, about (causal) laws: We could say that people’s use of counterfactual statements is aimed precisely at conveying generic causal information, uncontaminated by specific, transitory observations, about the real world. Observed facts often do reflect strange combinations of rare eventualities … that have nothing to do with general traits of influence and behavior. The counterfactual sentence, however, emphasizes the law-like, necessary component of the relation considered. (Balke and Pearl 1994: 231) ⮭
- Two more from Humberstone (2011):
⮭
(i) a. If there was pepper in the tea, I didn’t taste it. b. If there had been pepper in the tea, I wouldn’t have tasted it. (ii) a. If there is a kitten in this room, it is concealed from view. b. If there were a kitten in this room, it would be concealed from view. - They are not independent. In contemporary English, a counterfactually marked antecedent requires an (agreeing) modal auxiliary in the consequent. Nevertheless, (1) is not a minimal pair, for reasons it is the task of this paper to elaborate. ⮭
- See, e.g., Leahy (2018: 58). Note that a stronger counterfactuality is indicated by the “two-past” or pluperfect form ‘had been’ (where the clause is interpreted to apply to the present or future; the tense is, in that sense, “fake”). The difference is that the “two-past” conditional is infelicitous unless the antecedent is known to be false (see, e.g., Tellings 2016: 12–13). ⮭
- The restriction was first observed by Goodman (1947: 119–120). ⮭
- Some hope to derive the restriction from the baseline difference in felicity where the antecedent is known to be false (following Stalnaker 1975). Others simply include it in the meaning of the counterfactual morphology (Kaufmann 2013: 1139–40; Starr 2014: 1039). Either way, the restriction is attributed to the counterfactuality of (1b). ⮭
- For some or all of the theses that follow, consult Bennett (2003), Gibbard (1981), Harper (1981), Kratzer (2012), Kripke (1980), Lewis (1973: 74–77; 1979), Pearl (2009), Stalnaker (1975), Williamson (2007). It is worth pointing out that contemporary accounts in linguistics and philosophy occupy a range of positions that do not simply endorse all these theses, but rather select and refine them. See, for instance, Kaufmann (2013) for a developed example. ⮭
- We henceforth treat this arrangement as diagnostic of the inferential use. Note that will does not advert, in such cases, to some future moment of (direct) confirmation. The sentence is felicitous whether or not we anticipate such confirmation (cf. Cariani 2020: 346–49). Unlike some theorists, we choose to maintain a distinction between the future and inferential uses, since we believe there are cases where the inferential evidential restriction is absent and the contribution of will is purely temporal. Of course, it is unusual for a speaker to claim non-inferential acquaintance with an event occurring in the future, but examples do crop up in speculative fiction (e.g., the title story from Chiang 2002). ⮭
-
Condoravdi (2002), Werner (2003; 2006), Kaufmann (2005), Klecha (2014). Note will passes the basic test for being a “strong” necessity modal (von Fintel and Iatridou 2008):
⮭
(i) #Alma will be home right now, though she might not be. - Kratzer (2012: 9). On her account, the premise set is determined by the world of evaluation and certain features of the context of utterance (2012: 8–11). Together, these parameters first settle an initial broad base of propositions—the modal base—and a further means of ordering them—the ordering source (2012: 39). See Kaufmann (2013: 1140–43) for a quick refresher on Kratzer’s semantics. ⮭
- Will and must are thus inferential evidentials, a subvariety of indirect evidential in Willett’s (1988) taxonomy. The inference that licenses the evidential also establishes the “necessity” of the prejacent. For more on modals and evidentials, see Kratzer (2012: 21–23) and references therein. ⮭
- Anaphoricity is the requirement that the premises of the inference are public: perceptually available, recently asserted, or just generally known (Stone 1994). By contrast, will seems to require that some premises be known only to the speaker (Winans 2016: 22). ⮭
- Peirce (1883: 145) first defines abduction as an inverted syllogistic inference that runs from a “result” to the “case” responsible for generating it. Over time, this gets extended to inventing a hypothesis that would explain a surprising fact. Note that abduction in our sense is not meant to be an alternative to, or exclusive of, what is normally meant by deductive (or valid) inference. ⮭
- Note we can say, in the same situation:
Winans argues (2016: ch. 3) that this follows on her account. The prejacent of will in (i) is the proposition the smoky smell is (the smell of) the neighbours barbecuing, which is of course not the same as the proposition the neighbours are barbecuing. While the latter proposition fits the schema ‘there is a smoky smell because ’, the former does not. ⮭
(i) That will be the neighbours barbecuing. - Our broader sense of explanation follows Kment (2014: 5):
⮭To say that explains is to say that is the reason why obtains, or that is due to . Explanation in this sense is a metaphysical relation, not an epistemic one. A cause partly explains its effect, but can also partly explain without being a cause of .
- Winans 2016: 58. The languages with a counterpart of will (among those she surveys) are: Spanish, Catalan, Turkish, Dutch, German, Greek, Hindi, and Korean. ⮭
- As we will see in §5.1, will aligns with would on this empirical detail (the two discoveries were independent). Thanks to Will Starr (p.c.) for help with this comparative observation. ⮭
- Bjorndahl and Snider (2015) are the first (we know of) to argue that anti-abductivity (in the sense of §2) characterizes the behaviour of would-counterfactuals. ⮭
- Specifically, the proposition denoted by the prejacent of the modal auxiliary construction in the consequent. ⮭
- The reasoning in question may be nonmonotonic, which means that adding the hypothesis to the base facts has the potential (in principle) to destroy an existing inference from alone to . So understood, (9) extends to cases where is used to say that would still follow (from ) even if A had been so. Here is an example of such a counterfactual from Shakespeare’s 1 Henry IV:
⮭Glendower
… and at my birth
The frame and huge foundation of the earth
Shaked like a coward.
Hotspur
Why so it would have done at the same season
If your mother’s cat had but kittened, though yourself
Had never been born.
- Kratzer’s benchmark papers provide the standard translation (see her 2012, as well as Lewis 1981; 1973: 67). See Bennett (2003) and Williamson (2007) for arguments against the inferential approach. ⮭
- A famous illustration of the fact that conflicting conditionals may be licensed by different implicit premises is Gibbard’s (1981) riverboat example (cf. Kratzer 2012: 102–3). Leahy (2018: 64ff.) argues that the point extends to counterfactuals. ⮭
- The following are similar (cf. Balke and Pearl 1994: 230):
The supplementary premise can alternatively be appended by since:
(i) Given that it is now 2020, a. If Alma had been born in 2000, she would be turning 20. [True] b. If Alma had been born in 2000, it would now be 2040. [False/#] (ii) Given that Alma is turning 40, a. If she had been born in 2000, she would be turning 20. [False/#] b. If she had been born in 2000, it would now be 2040. [True] Note that supplementary premises, being factual, occur in the indicative mood and are not presented as hypothetical (we introduce them with since or ‘given that’ rather than if ). ⮭(iii) If Alma had been born in 2000, she would be turning 20, since it is now 2020. (iv) If Alma had been born in 2000, it would now be 2040, since she is turning 40. - Compare Stone (1994: 189), Kratzer (2012: 6). ⮭
- Both inferences rely, of course, on the background assumption that the grass is wet if and only if either it has rained or the sprinkler was on. ⮭
- Should a compositional morphological derivation be appropriate. ⮭
- The same goes for another famous illustration of the distinction. In the following pair (Adams 1970: 90), we naturally interpret the (woll-free) indicative as true by virtue of an obvious abduction from the circumstances of Kennedy’s death:
Abduction is not permitted in the would-counterfactual, which means the interpreter is required to insert a more paranoid argument that is not based on the premise of his violent death. ⮭
(i) a. If Oswald didn’t kill Kennedy, someone else did. b. If Oswald hadn’t killed Kennedy, someone else would have. - Jonathan Bennett (2003: 274) connects ‘would have to’ to abduction:
Similarly, Bjorndahl and Snider (2015: 10, fn. 3) argue that the abductive pattern corresponds to a different reading of the conditional (licensed by the double auxiliary in the consequent, 2015: 8–9). ⮭[The auxiliary verb have’s] real point is to register the thought that … the consequent is acceptable as the best explanation for … the antecedent. If the plane arrived at 2 p.m., that would have to have been because it left at noon—the modal ‘have to’ expresses the compulsion in our being forced to that explanation for lack of any other as good.
- Other auxiliary structures work too. For instance:
It seems that counterfactual compatibility modals allow abduction (Arregui 2005: 89, although cf. 93). While it is possible to formulate anti-abductivity for such modals (see fn. 40), they do not seem to carry the constraint. (Thanks to Will Starr p.c. for pressing us to consider compatibility modals.) ⮭
(i) If the grass had been dry, the sprinkler couldn’t have been on. [True] - Under the heading of “backtracking” counterfactuals. See Lewis (1979: 458) for a famous discussion. Also Frank 1997 and Arregui 2005. ⮭
- See, e.g., Davis 1979: 561. Note the embedded necessity analysis is appropriate for an example like the following:
Here we can isolate the state of medical necessity that would have ensued had the patient not died. It is less clear how to achieve a similar breakdown of (22), as there is no corresponding precept or goal requiring the sprinkler to be on (in the event of no rain, but wet grass). Besides, other abduction permitting constructions only have one auxiliary (see fn. 29), so this tactic will not work generally. ⮭
(i) An autopsy revealed that his legs had been so badly damaged that if he hadn’t died, they would have to have been amputated. - Cf. Balke and Pearl 1994: 232. An indicative analysis is hard to square with the fact that (22) is felicitous when the antecedent is known to be false—the hallmark of the counterfactual conditional. One could draw the indicative/counterfactual boundary differently, but there is pressure to group would- and ‘would have to’-conditionals together, as both auxiliary structures can occur on different clauses of the same consequent (cf. Humberstone 2011: 943–44):
Furthermore, a ‘would have to’-clause cannot occur in parallel with an indicative clause in the consequent:
(i) If it hadn’t rained, the grass would be dry or else the sprinkler would have to have been on. ⮭(ii) *If it hasn’t/hadn’t rained, the grass is dry or else the sprinkler would have to have been on. - Schulz does propose that the extra auxiliary have makes the epistemic reading prominent (2007: 88–91, 128). Nevertheless, she seems committed to would-counterfactuals having epistemic readings (see 2007: 88–89 and the parenthetical at 2007: 91). ⮭
- While English would is a case where the counterfactual (i.e., past tense) morphology may be separated from the morpheme contributing anti-abductivity (woll), we do not expect or claim that this should be the case more generally or cross-linguistically (we thank Nathan Klinedinst p.c. for pressing us on this). Indeed, English itself shows a less perspicuous pattern when it comes to the abductive paradigm: ‘would have to’ is unrelated to must, and even contains would as a part. ⮭
- See Karawani (2014) for a recent taxonomy. ⮭
- One could even argue that the ability to distinguish types of inference (with abductive and anti-abductive forms) is particularly useful in the counterfactual domain, where the same hypothesis, supplemented by different facts, can deliver conclusions that are in conflict (see §3.1). ⮭
- This section adapts Bjorndahl and Snider’s (2015) account of anti-abductivity in would-counterfactuals. For an alternative formal approach, see Krawczyk (2012). ⮭
- While Pearl, who inaugurated the use of SEMs in semantic theory, takes each boolean expression to model autonomous causal processes, we generalize this understanding to other (metaphysically) explanatory relationships (cf. Schaffer 2016). ⮭
- We assume an acyclic parent relation, so that a truth assignment can always be computed from an arbitrary assignment to the exogenous variables (i.e., ). ⮭
- Though initially presented as a constraint on inference, anti-abductivity can be generalized to any modal operator that relates its prejacent to a further set of propositions—whether by entailment, compatibility, or something in between. ⮭
- The truth-value of a logically complex formula (metaphysically) depends on the truth-values of the boolean variables that occur within it—at least to a first approximation (cf. Rosen 2010). Note that the atom function is applied to merely to strip off negation if present (cf. Bjorndahl and Snider 2015: 12, fn. 4)—a modal auxiliary cannot embed a proposition more complex than a negated atom. Also, to improve legibility, we allow atom to extract all the members of Var occurring in a set of formulas, and extend the definition of to unit sets of variables in the obvious way. ⮭
- While must requires the contents of to be public, (anti-anaphoric) will requires some members of (or else some parts of ) to be absent from the public record at the time of utterance. Note that we don’t try to represent this requirement in (28). Neither do we offer an account of how is settled (for an anti-anaphoric auxiliary), except to assume that the speaker’s (public or private, explicit or implicit) commitment to certain inferential grounds will be a leading factor. ⮭
- , with a set of formulas, means follows from by logic alone (i.e., without seeing the dependencies in ) ; in other words, every function that verifies all the formulas in , also verifies . Clause (b) ensures that, if there is direct evidence for , the speaker is not (trivially) inferring it on those grounds (i.e., from itself or some other proposition that logically entails it). Instead must receive an indirect justification, operationalized here as an inference that goes via the (non-logical) dependencies in (cf. von Fintel & Gillies 2010; Schulz 2007: 137). ⮭
- , with a set of formulas, holds iff every truth assignment for that verifies all formulas in also verifies . ⮭
- For an analysis of the anaphoricity of must, see Stone (1994). ⮭
- Some judgments in this paper suggest that must is bad unless the inference is abductive. Stone (1994: 183) offer clear examples to the contrary, so we don’t require this of must (or ‘would have to’), and trust that the infelicities may be explained as the result of a different violation (e.g., of anaphoricity). ⮭
- As the following contrast demonstrates, extending this account to logically complex consequents is not straightforward (we leave it to future work):
We would like to explain the contrast by showing that the right disjunct of the consequent partially explains the antecedent or a member of the premise set (and hence cannot pair with an anti-abductive modal). However, is not an -ancestor of , and the premise set is empty—the disjunctive consequent follows from the antecedent alone (i.e., ). It may be that anti-abductivity is not correctly formulated. On the other hand, we could see what happens if the inference to each disjunct in the consequent is considered, and gauged for abductivity, separately. To infer a disjunct outright, we would need the negation of the other disjunct as an additional (hypothetical) premise (see Krahmer and Muskens 1994 for a similar suggestion with independent motivation). The inference to from and is abductive, since, , but the inference to the other disjunct is not. Hence this would be a way to predict the pattern we see without needing to alter our definition of abduction. ⮭
(i) If it hadn’t rained, the grass would be dry or else the sprinkler would have been on. [False/#] (ii) If it hadn’t rained, the grass would be dry or else the sprinkler would have to have been on. [True] - Cf. Kaufmann (2013: 1142). We have not made the same replacement in (a) because the antecedent is not required to be factual. ⮭
- Note that this requires that is consistent (otherwise every proposition would be a trivial consequence). We do not represent, in (30), any further constraint on the antecedent, beyond consistency with the premise set. In particular, we do not represent the requirement, contributed by the indicative mood, that is not supposed false. Consult Starr (2014) for an analysis of indicative and counterfactual conditional antecedents in dynamic semantics. ⮭
- As we have noted (§3.2), judgments pertaining to the abductivity of the supporting inference carry over from indicatives to the corresponding counterfactuals:
⮭
(i) a. If it has rained, the grass will be wet. [True] b. If it hasn’t rained, the sprinkler must have been on (since the grass is wet). [True] (ii) a. If it had rained, the grass would be wet. [True] b. If it hadn’t rained, the sprinkler would have to have been on (since the grass is wet). [True] - This is very rough. A better approximation would be to split the variable between triggering and inhibiting abnormalities, so that the equation becomes (cf. Pearl 2009: 29). ⮭
- The discussion to follow is in line with Hobbs, Stickel, Appelt, and Martin (1993: 85–87), who assume that normality claims will not be among the theorems of the knowledge base. ⮭
- Worse still, for an anaphoric modal such as must, the premise would need to be common ground. ⮭
- Note that something in the vicinity is what the felicity of certain “Heim sequences” turns on. See Moss (2012) and especially the discussion in Lewis (2018: 488–89). ⮭
- Note that “epistemic” should and ought are anti-abductive:
Cf. Krzyżanowska, Wenmackers, and Douven (2013). ⮭
(i) It ought to/should have rained, since the grass is wet. [False/#] - See, e.g, Kment 2014, Sloman and Lagnado 2005. ⮭
- Boris Kment’s proposal about the nature of metaphysical modality and modal reasoning is clearly inspired by the interventionist account of counterfactuals:
⮭The function of modal thought is to facilitate a common type of thought experiment—counterfactual reasoning—that allows us to investigate explanatory connections and which is closely related to the controlled experiments of empirical science. Necessity is defined in terms of explanation, and modal facts often reflect underlying facts about explanatory relationships. The study of modal facts is important for philosophy, not because these facts are of much metaphysical interest in their own right, but largely because they provide evidence about explanatory connections. (Kment 2014: 1–2)
- Here we follow Hiddleston 2005. ⮭
- If is not downstream of , then is only true if is (by option (b)). We can think of this case as dispensing with inferential support, or else (incorporating a bit more of the interventionist algorithm) as requiring exclusively forward inference (from the facts of the causal background responsible for bringing about ). ⮭
- The background model () relates three propositions—the firework denonated (), there was a flash (), there was a bang ()—by the dependencies , . The truth-assignment () is such that ). By (38), the truth-value of in corresponds to that of in , where . Now and (this formula is unchanged) in . Hence . ⮭
- Commenting on Downing’s (1959) example (below), Lewis notes (1979: 456–57) that backtracking arguments are typically obscured by more straightforward ones; linguistic scaffolding is necessary to bring them into focus. For example, an immediate inference supports the consequent of (i), obscuring the backtracking inference to the opposite conclusion, until the necessary lemma (the common cause of the antecedent and the consequent of (iii)) is established by the intervening (abductive) counterfactual (ii):
⮭
(i) Jim and Jack quarreled yesterday, and Jack is still hopping mad. We conclude that If Jim asked Jack for help today, Jack would not help him. (ii) But wait: Jim is a prideful fellow. He never would ask for help after such a quarrel; If Jim were to ask Jack for help today, there would have to have been no quarrel yesterday. (iii) In that case Jack would be his usual generous self. So If Jim asked Jack for help today, Jack would help him after all. - Hiddleston (2005) develops a semantics that predicts the truth of (39) by relaxing interventionism’s strict prohibition on abductive steps. However, he does so in a way that fails to distinguish abduction (‘backwards’) from common cause (‘backtracking’) inference. Whenever it is possible to infer via a common cause on his semantics, it is also possible to stop one step short and infer to that cause (i.e., abductively). His account, therefore, does not generate the empirical contour just described. The same criticism extends to more recent models that pursue the same approach of relaxing anti-abductivity to enable common cause inference, including Rips’s (2010) minimal network model and Lucas and Kemp’s (2015) extended structural model. ⮭
- See (3) in §2, and the discussion (of clause (b)) in (28) and (30). See also Goodman (1947: 117–19). ⮭
- See, e.g., Bennett (2003: 235) for an attempt. ⮭
- A random outcome cannot be inferred from the prior state of the universe. The alternatives are trivial inference (ruled out by nontriviality) and abductive inference (ruled out by anti-abductivity). This explains why would-counterfactuals whose consequents state a random outcome (as opposed to a nontrivial consequence of such an outcome) tend to be false. ⮭
- Further evidence that reasoning from the truth of the consequent is not permitted is that when the premise is explicit, the result is clearly infelicitous:
The same goes for reasoning from the falsity of the antecedent:
(i) #But even if it had not been raining, Jones would have been wearing his hat, since he is wearing his hat. (ii) #If Smith had tossed the coin instead of Jones, it would still have landed heads, since it landed heads. Note that being explicit is fine in those cases where the judgment is true:(iii) #But even if it had not been raining, Jones would have been wearing his hat, since it has been raining. ⮭(iv) But even if it had not been raining, Jones would have been wearing his hat, since the coin landed heads. [True] (v) If Smith had rolled the dice instead of Jones, he would have been home, since they came up double six. [True] - This (correct) prediction rests on the assumption that the generalization has the wording in the text. If instead it is: ‘Whenever it rains or the sprinkler is on, the grass is wet’, then those predictions are reversed, since the alternative situation where the sprinkler is on and the grass is wet will be confirmatory instead. Kratzer’s account therefore appears overly subtle. Whichever wording is used, it seems, we judge (13) true and (14) false/infelicitous. ⮭
- The case is borrowed from Bjorndahl and Snider (2015). ⮭
- As opposed to the asymmetric structural equation (with dependent variable on the left). Here is Alice goes to the party and is Bob goes to the party. ⮭
- Kratzer’s complete approach includes a further piece of apparatus, a relation between propositions she terms lumping (2012: 118). Suppose one day Paula paints a still life that includes some apples and some bananas. The proposition that Paula painted a still life (on that occasion) lumps (relative to the actual world) the proposition that she painted apples and the proposition that she painted bananas (2012: 113). The truth-makers of lumped propositions are not independent: the minimal situation that makes the proposition that she painted apples true is a part of the minimal situation that makes the proposition that she painted a still life true. While lumping is not a causal notion, it is based on other (i.e., noncausal) relations of metaphysical dependency. Roughly speaking, whenever one proposition lumps another , depends (non-causally) on . In the case of Paula’s still life, the metaphysical dependency is underwritten by the composition relation (Bennett 2017: 8). For our part, we agree with Kratzer that would-counterfactuals are sensitive to lumping, since we believe they are sensitive to noncausal metaphysical dependency (recall example (6)). (Note that for us, the specific relationship is the one set out in (24), which differs from Kratzer’s own account. Note further that we would not necessarily agree with all of the applications of lumping in her 2012: at least some of the problem cases she considers are better explained as violations of nontriviality.) However, we also believe they are sensitive to causal dependency. We take both forms of sensitivity to spring from a general ban on abduction. ⮭
- We can either suppose that the king’s departure resulted in the lights being turned off, or that the flag’s staying up played a role in this too. Either way, the lights’ being off is not a causal ancestor of either premise. ⮭
- If the king is home (the conclusion of (46a)), then the lights must be on, not off. Compare the discussion of backtracking arguments in fn. (61). ⮭
- Kratzer, too, shows that the effect can be reversed (2012: 145). While we are sympathetic to her account in this case, we maintain that the approach fails to be general, and in particular does not suffice to explain the judgment in (14). Though (47) is true, a similar attempt to repair (14) by filling in the supplementary premise fails, as we have already noted:
⮭
(i) #If it hadn’t rained, the sprinkler would have been on, since the grass is wet. - Reportative evidentials mark the former, inferential evidentials the latter. The broader category of indirect justification covers both (see Willett 1988). ⮭
- The self-talk is used to get around the anti-anaphoricity confound. The oddness persists if instead you are speaking to a companion who is blind and cannot read the sign. ⮭
- The story just told also predicts will to be bad in the following conditionals (since the improvement is wrought by the auxiliary would, rather than the conditional structure):
The judgments, though weaker in the (a) example, are in the expected direction of preference for the clause without will. Moreover, the contrast between will and would seems clear (would in (53) is impeccable). ⮭
(i) a. If there is a ‘closed’ sign on the door, the library? will be/is closed. b. If the referee has blown the whistle, the game?? will be/is over. - Recall (from fn. 3) that the consequent of a counterfactual (in contemporary English) is required to include a modal auxiliary. ⮭
- It is not clear that the analogy holds for the future sense, which may not (consistently) impose an evidential constraint (in which case it is a fortiori not anti-abductive). See fn. 8. ⮭
- Cariani and Santorio (2018) propose a modal (selection function) semantics for woll (and hence common to both will and would). However, as they spell out (2018: 147–148) the selection function ends up being vacuous for unembedded will, and hence the account does not generate any substantial constraint in common for inferential will and counterfactual would. ⮭
- Dancygier and Mioduszewska (1984) come close with their category of “consequential” conditionals. They note many of the same empirical patterns, but neither they, nor Humberstone—who contributes a further observation (2011: 943)—put things together the way we do. Humberstone, in particular, downplays the importance of “consequentiality” (by comparison to counterfactuality), citing the sort of “amalgamations” we discuss in fn. 32. ⮭
References
Abusch, Dorit (1997). Sequence of Tense and Temporal de re. Linguistics and Philosophy, 20(1), 1–50.
Adams, Ernest J. (1970). Subjunctive and Indicative Conditionals. Foundations of Language, 6(1), 89–94.
Arregui, Ana (2005). On the Accessibility of Possible Worlds: The Role of Tense and Aspect (Unpublished doctoral dissertation). University of Massachusetts, Amherst.
Balke, Alexander and Judea Pearl Barbara Hayes-Roth and Richard Korf (Eds.), Proceedings of the Twelfth National Conference on Artificial Intelligence (230–37).
Bennett, Jonathan (2003). A Philosophical Guide to Conditionals. Oxford University Press.
Bennett, Karen (2017). Making Things Up. Oxford University Press.
Bjorndahl, Adam and Todd Snider (2015). Informative Counterfactuals. In Sarah D’Antonio, Mary Moroney, and Carol Rose Little (Eds.), Proceedings of SALT 25 (1–17).
Cariani, Fabrizio (2020). On Predicting. Ergo, 7(11), 339–61.
Cariani, Fabrizio and Paolo Santorio (2018). Will Done Better: Selection Semantics, Future Credence, and Indeterminacy. Mind, 127(505), 129–65.
Chiang, Ted (2002). Stories of Your Life and Others. Tor Books.
Chisholm, Roderick M. (1946). The Contrary-to-Fact Conditional. Mind, 55(220), 289–307.
Condoravdi, Cleo (2002). Temporal Interpretations of Modals: Modals for the Present and for the Past. In David Beaver, Stefan Kaufmann, Brady Clark, and Luis Casillas (Eds.), The Construction of Meaning (59–88). CSLI.
Dancygier, Barbara and Ewa Mioduszewska (1984). Semanto-Pragmatic Classification of Conditionals. Studia Anglica Posnaniensia (An International Review of English Studies), 17, 121–33.
Davis, Wayne A. (1979). Indicative and Subjunctive Conditionals. Philosophical Review, 88(4), 544–64.
Downing, P. B. (1959). Subjunctive Conditionals, Time Order, and Causation. Proceedings of the Aristotelian Society, New Series, 59, 125–40.
Dudman, Victor H. (1988). Indicative and Subjunctive. Analysis, 48(3), 113–22.
Dudman, Victor H. (2001). Three Twentieth-Century Commonplaces about ‘If’. History and Philosophy of Logic, 22, 119–27.
von Fintel, Kai and Anthony S. Gillies (2010). Must … Stay … Strong! Natural Language Semantics, 18(4), 351–83.
von Fintel, Kai and Sabine Iatridou (2008). How to Say Ought in Foreign: The Composition of Weak Necessity Modals. In J. Guéron and J. Lecarne (Eds.), Time and Modality: Vol. 2. Studies in Natural Language and Linguistic Theory (115–41). Springer.
Frank, A. (1997). Context Dependence in Modal Constructions (Unpublished doctoral dissertation). University of Stuttgart.
Gibbard, Allan F. (1981). Two Recent Theories of Conditionals. In William L. Harper, Robert C. Stalnaker, and G. Pearce (Eds.), Ifs: Conditionals, Beliefs, Decision, Chance, Time (211–47). D. Reidel.
Gibbard, Allan F. and William L. Harper (1978). Counterfactuals and Two Kinds of Expected Utility. In Clifford Hooker, James J. Leach, and Edward McClennen (Eds.), Foundations and Applications of Decision Theory (125–62). D. Reidel.
Goodman, Nelson (1947). The Problem of Counterfactual Conditionals. The Journal of Philosophy, 44(5), 113–18.
Harper, William L. (1981). A Sketch of Some Recent Developments in the Theory of Conditionals. In William L. Harper, Robert C. Stalnaker, and G. Pearce (Eds.), Ifs: Conditionals, Beliefs, Decision, Chance, Time (3–38). D. Reidel.
Hiddleston, Eric (2005). A Causal Theory of Counterfactuals. Noûs, 39(4), 632–57.
Hobbs, Jerry, Mark E. Stickel, Douglas E. Appelt, and Paul Martin (1993). Interpretation as Abduction. Artificial Intelligence, 63(1–2), 69–142.
Humberstone, Lloyd (2011). The Connectives. MIT Press.
Ippolito, Michela (2016). How Similar Is Similar Enough? Semantics and Pragmatics, 9(6), 1–60.
Karawani, Hadil (2014). The Real, the Fake, and the Fake Fake in Counterfactual Conditionals, Crosslinguistically (Unpublished doctoral dissertation). University of Amsterdam.
Karttunen, Lauri (1972). Possible and Must. In John Kimball (Ed.), Syntax and Semantics (Vol. 1, 1–20). Seminar.
Kaufmann, Stefan (2005). Conditional Predictions. Linguistics and Philosophy, 28(2), 181–231.
Kaufmann, Stefan (2013). Causal Premise Semantics. Cognitive Science, 37(6), 1136–70.
Klecha, Peter (2014). Diagnosing Modality in Predictive Expressions. Journal of Semantics, 31(3), 443–55.
Kment, Boris (2014). Modality and Explanatory Reasoning. Oxford University Press.
Krahmer, Emiel and Reinhard Muskens (1994). Umbrellas and Bathrooms. In M. Harvey and L. Santelmann (Eds.), Proceedings of SALT IV (179–94).
Kratzer, Angelika (2012). Modals and Conditionals. Oxford University Press.
Krawczyk, Elizabeth A. (2012). Inferred Propositions and the Expression of the Evidence Relation in Natural Language Evidentiality in Central Alaskan Yup’ik Eskimo and English (Unpublished doctoral dissertation). Georgetown University.
Kripke, Saul (1980). Naming and Necessity. Harvard University Press.
Krzyżanowska, Karolina, Sylvia Wenmackers, and Igor Douven (2013). Inferential Conditionals and Evidentiality. Journal of Logic, Language and Information, 22(3), 315–34.
Leahy, Brian (2018). Counterfactual Antecedent Falsity and the Epistemic Sensitivity of Counterfactuals. Philosophical Studies, 175, 45–69.
Lewis, David K. (1973). Counterfactuals. Harvard University Press.
Lewis, David K. (1981). Ordering Semantics and Premise Semantics for Conditionals. Journal of Philosophical Logic, 10(2), 217–34.
Lewis, David K. (1979). Counterfactual Dependence and Time’s Arrow. Noûs, 13(4), 455–76.
Lewis, Karen (2018). Counterfactual Discourse in Context. Noûs, 52(3), 481–507.
Lucas, Christopher G. and Charles Kemp (2015). An Improved Probabilistic Account of Counterfactual Reasoning. Psychological Review, 122(4), 700–734.
Moss, Sarah (2012). On the Pragmatics of Counterfactuals. Noûs, 46(3), 561–86.
Pearl, Judea (1996). Causation, Action, and Counterfactuals. In Alexander Gammerman (Ed.), Computational Learning and Probabilistic Reasoning (103–24). John Wiley and Sons.
Pearl, Judea (2009). Causality: Models, Reasoning, and Inference (Second Edition). Cambridge University Press.
Charles Sanders Peirce (1883). A Theory of Probable Inference. In Charles Sanders Peirce (Ed.), Studies in Logic by Members of the Johns Hopkins University (126–81). Little, Brown, and Co.
Pollock, John L. (1976). Subjunctive Reasoning. D. Reidel.
Rips, Lance J. (2010). Two Causal Theories of Counterfactual Conditionals. Cognitive Science, 34(2), 175–221.
Rosen, Gideon (2010). Metaphysical Dependence: Grounding and Reduction. In Bob Hale and Aviv Hoffmann (Eds.), Modality: Metaphysics, Logic, and Epistemology (109–35). Oxford University Press.
Schaffer, Jonathan (2016). Grounding in the Image of Causation. Philosophical Studies, 173, 49–100.
Schulz, Katrin (2007). Minimal Models in Semantics and Pragmatics: Free Choice, Exhaustivity, and Conditionals (Unpublished doctoral dissertation). ILLC, Amsterdam.
Sloman, Steven A. and David A. Lagnado (2005). Do We “Do”? Cognitive Science, 29(1), 5–39.
Stalnaker, Robert C. (1975). Indicative Conditionals. Philosophia, 5, 269–86.
Starr, William B. (2014). A Uniform Theory of Conditionals. Journal of Philosophical Logic, 43(6), 1019–64.
Stone, Matthew (1994). The Reference Argument of Epistemic Must. In Harry Bunt, Reinhard Muskens, and Gerrit Rentier (Eds.), Proceedings of IWCS 1 (181–90).
Tellings, Jos (2016). Counterfactuality in Discourse (Unpublished doctoral dissertation). University of California, Los Angeles.
Tichý, Pavel (1976). A Counterexample to the Stalnaker-Lewis Analysis of Counterfactuals. Philosophical Studies, 29(4), 271–73.
Veltman, Frank (2005). Making Counterfactual Assumptions. Journal of Semantics, 22(2), 159–80.
Werner, Thomas A. (2003). Deducing the Future and Distinguishing the Past: Temporal Interpretation in Modal Sentences in English (Unpublished doctoral dissertation). Rutgers, The State University of New Jersey.
Werner, Thomas A. (2006). Future and Non-Future Modal Sentences. Natural Language Semantics, 12, 235–55.
Willett, Thomas (1988). A Cross-Linguistic Survey of the Grammaticalization of Evidentiality. Studies in Language, 12(1), 51–97.
Williamson, Timothy (2007). The Philosophy of Philosophy. Oxford University Press.
Winans, Lauren (2016). Inferences of “will” (Unpublished doctoral dissertation). University of California, Los Angeles.