1. Introduction
There is something noteworthy about the reception of reflective equilibrium (RE) in the philosophical literature: while the method has been widely discussed and often invoked, there have been almost no attempts at making it formally precise. The popularity of RE is most notable in ethics, where leading scholars have committed themselves to RE (see, e.g., Beauchamp & Childress 2013; Daniels 1996; DePaul 2011; Mikhail 2011; Rawls 1999; Swanton 1992; van der Burg & van Willigenburg 1998). But RE also figures prominently in methodological discussions in logic (e.g., Goodman 1999; Peregrin and Svoboda 2017; Resnik 1985; 1996; 1997; 2004; Shapiro 2000) and theories of rationality (e.g., Cohen 1981; Stein 1996). Some authors even claim RE to be the method of philosophy (Lewis 1983: x; Keefe 2000: Ch. 2) or defend it as a general account of epistemic justification (Elgin 1996; 2017).
Indeed, the main idea behind RE does sound very plausible: You start from prior commitments about a topic and try to account for them in terms of a systematic theory, which may be thought of as a set of principles. Once you have identified a theory which accounts for many of the commitments, you reconsider the commitments and readjust some of them to obtain a better fit with the theory. By going back and forth between commitments and theory and by adjusting them to each other, you arrive at an equilibrium state in which commitments and theory cohere and thus support each other.
However, all this is quite vague, and the method has not been worked out in a precise way. Even the most elaborate characterizations of RE (Baumberger & Brun 2016; Daniels 1996; DePaul 2011; 1993; Elgin 1996; 2017; Tersman 1993) do not specify rules for choosing principles that systematize the commitments; and existing characterizations of equilibrium states are based on rather vague and metaphorical notions such as coherence and equilibrium. It thus may be complained that RE is too permissive to be of any use (e.g., Foley 1992; Singer 2005); or it may be doubted that there is, in fact, a tenable core idea that underlies the existing accounts of RE and that allows for consistent elaboration (Williamson 2007). It may also be worried that any discussion about the merits and pitfalls of the method (see, e.g., Bonevac 2004; Kelly & McGrath 2010; Singer 2005; Tersman 2018) is premature unless it is clear what the method involves. Although there are proposals for a formal specification of at least some aspects of RE (Tersman 1993; Thagard 2000; Yilmaz, Franco-Watkins, and Kroecker 2017), they remain under-explored and have not been referred to in critical discussions of RE.
This paper aims to allay the doubts and worries just voiced by developing and investigating a formal model of RE. The model is subject to the following requirements: (i) It is supposed to be faithful to the core idea of RE as specified above; (ii) It is fruitful in that it provides insights about RE, offers conceptual clarification of crucial issues, and provides a tool to address and answer key questions about RE.
Our model contains counterparts of the most important components of RE, characterizes equilibrium states and specifies a system of rules to get there (Sect. 2; technical details are relegated to Appendix A). The rules can be applied by a computer, and we use a computer program to study the behavior of the model with simple examples (Sect. 3). We show that our model satisfies the requirements (i) and (ii) above (Sect. 4). In particular, since the model has solutions, it is consistent, which implies the possibility to consistently specify RE. Further, the model can be used to check to what extent worries about RE are legitimate.
We call the main proposal of this paper a model since it differs from earlier characterizations of RE in terms of abstractions and idealizations. Thus, our model offers a simplified surrogate of RE. Nevertheless, our model has the aspiration to faithfully represent the core idea of the method, as specified above. In this respect, the model goes beyond the very few available attempts at giving a formal account of RE, because Tersman (1993), Thagard (2000) and Yilmaz et al. (2017) focus on a formal characterization of coherence and do not, e.g., distinguish commitments from theories. As we show in Sect. 4, the abstractions and idealizations of the model do not compromise its ability to fulfill its aims. The model is formal because it is specified in a formal framework, the Theory of Dialectical Structures (”TDS“ for short; Betz 2010; 2012).
In this paper, we concentrate on what is called “proof of concept”: We show that the model works for the intended purposes. A closer investigation of the model’s behavior as well as further development of the model is left to future work (see our conclusions in Sect. 5).
2. The Model
Let us begin by introducing our model. A discussion of its justification and limitations is left to Sect. 4. The core idea that guides the design of our model (see the second paragraph of the introduction) goes back to Goodman (1999: Ch. 3) and Rawls (1999: in particular §4 and §9; see also Rawls 1975), but we draw especially on the elaborations of RE due to Elgin (1996; 2017), Brun (2014), and Baumberger and Brun (2016; 2020).
2.1. Basic Components of the Model
Topic:
RE is a method for justifying a view about a particular topic (e.g., trolley cases, the just design of political institutions, or the fine arts). We represent a topic as a “sentence pool”, i.e., a set of sentences that are relevant to the topic. We assume: (1) The sentence pool is closed under negation, i.e., it also comprises the negation of each sentence it includes. (2) The sentence pool is fixed, i.e., all relevant sentences are given from the beginning and do not change in the course of a RE process.
For example, the sentence pool representing the topic of trolley cases (see Thomson 2008) may contain sentences such as: “In the example ‘fat man’, it is impermissible to shove the fat man off the bridge to save five people,” “It is obligatory to save the largest number of lives possible,” “Morally speaking, unintended effects count less than intended ones,” etc.
Sentences that are relevant to a topic will typically be inferentially related to each other in various ways. We represent such inferential relations by deductively valid arguments, whose premises and conclusions are drawn from the sentence pool. We assume that the deductive relationships between sentences of the sentence pool—and thus the corresponding arguments—are given and fixed. We do not make any assumption about what grounds the validity (e.g., the form of the sentences, interrelations between concepts, etc.). In this respect, our model is intentionally uncommitted and allows for different interpretations and hence applications.
For example, the following argument
| (1) | In some trolley cases, it is impermissible to sacrifice the single person. |
| (2) | In all trolley cases, you cannot save both, the single person and the group of persons. |
| (3) | Thus: It is not always obligatory to save the largest number of lives possible. |
Commitments:
An agent’s commitments are the propositions relevant to the topic which the agent accepts. We model her commitments as a set of sentences from the sentence pool.2 The initial commitments, i.e., the commitments the agent starts with, are called ; the commitments that result from the ith opportunity to revise the commitments are symbolized as .3
We stipulate that commitments of an agent are always minimally consistent, i.e., an agent is never committed to a sentence and its negation at the same time. However, commitments need not be fully consistent; i.e., at some stage, the commitments may contain less-manifest contradictions (more on that below).For example, the commitments of an agent in the trolley-cases-topic might consist in premises (1) and (2) of the argument above.
For example, an agent might be committed to premises (1) and (2) of the argument above while accepting the negation of its conclusion. Her commitments would still be minimally consistent.
Moreover, we do not require that an agent takes a stance on every sentence that belongs to a topic. In other words, for some sentences, the commitments may contain neither the sentence nor its negation.
Theories:
We take theories to be sets of sentences from the sentence pool. Sentences which constitute a theory will also be called “principles.” Every sentence in the sentence pool is eligible as a principle. In particular, we do not restrict theories to law-like sentences. Law-likeness, or, more generally, systematicity of principles, will be spelled out in terms of the inferential properties of principles—see below. We use again sub-indices to label theories; thus is the theory that results from the th opportunity to choose a theory.
Unlike an agent’s commitments, theories are stipulated to be fully consistent. This is to say that they respect all inferential constraints given by the arguments: All sentences in the theory can consistently be assigned the truth value “true.” The content of a theory is the set of sentences which follow from its principles by means of the given deductive inferential relations.
For example, the set which contains only the sentence “It’s always obligatory to save the largest number of lives possible” is a theory with one principle. Whatever follows from this principle (given the available arguments)—e.g., “In the trolley case with two persons in the trolley, it is obligatory to save the largest number of lives possible”—belongs to the content of this theory. In particular, every conclusion of an argument with the above principle as the only premise is part of the theory’s content.
As the example illustrates, theories do not need to be complete; we allow for theories that do not take a stance on every sentence from a topic.
Epistemic State:
The epistemic state of an agent consists of her commitments and her theory, , where may equal or . In a given epistemic state, theory and commitments may, but need not, overlap with one another (see Rawls 1975 and Brun 2014).
2.2. Achievement Function and RE States
RE is supposed to make progress in justification. This requires standards or desiderata, as we will call them. We distinguish three key desiderata on epistemic states, all of which come in degrees: account, simplicity, and faithfulness. For each desideratum, we propose a measure that quantifies the extent to which it is realized. The larger the value of the measure, the higher is the degree to which the desideratum is fulfilled.
Account:
Loosely speaking, a theory accounts for the commitments to the extent to which it agrees with the commitments (e.g., Goodman 1999: 64).4 In our model, the principles that constitute a theory account for a single commitment if and only if the principles entail the commitment.
For example, in the topic of trolley cases, the theory with the principle “It is always obligatory to save the largest number of lives possible” accounts for the commitment “In the trolley case with two persons in the trolley, it is obligatory to save the largest number of lives possible.”
The degree to which a theory accounts for a set of commitments is a function of
| 1. | the number of commitments that are inconsistent with the theory; |
| 2. | the number of commitments that are not entailed by the theory; |
| 3. | the number of sentences in the content of the theory which the agent is not committed to. |
Systematicity:
A theory can be more or less systematic. In our model, the systematicity of a theory is determined by its simplicity. More precisely, the degree to which a theory is systematic is a function of
| 1. | the number of ’s principles; |
| 2. | the number of sentences in the content of . |
For example, in the trolley-cases-topic, suppose that the inferential relations in the sentence pool are such that the theory with the sole principle “It is always obligatory to save the largest number of lives possible” has many different implications. This means that the theory is very systematic.
Faithfulness:
An epistemic state and, specifically, its commitments can be more or less faithful to a given set of initial commitments, . In the terms of Brun (2014: 241), this is to say that they more or less respect the latter.7
Faithfulness can be specified in analogy to account. The degree to which current commitments are faithful to the set of initial commitments is a function of
| 1. | the number of initial commitments that are explicitly denied by the current commitments; |
| 2. | the number of initial commitments that are not current commitments. |
For example, in the topic of trolley cases, suppose that the agent was initially committed to premises (1) and (2) of the argument above (and nothing else), and that she is currently committed to the premises (1) and (2) and the argument’s conclusion (3) (and nothing else). Her current commitments are still maximally faithful to her initial ones.
How are the three desiderata—account, systematicity, and faithfulness—related? Note that systematicity applies to the theory only, while faithfulness is a matter of the commitments only. It is merely account that binds theory and commitments together. Yet, systematicity and faithfulness are nonetheless desiderata on the whole epistemic state, which consists of a set of commitments and a theory.
The desiderata can, and often will, pull in different directions. For instance, one can frequently account for more commitments by using less systematic theories. To handle such trade-offs, the desiderata have to be balanced against each other. A straightforward way of balancing the desiderata is to assign each desideratum a specific weight and to quantify the overall value of an epistemic state using the weighted sum of the measures. We hence introduce what we call the global achievement function, , which measures the overall value of an epistemic state.
where the weights , , are non-negative real numbers that add up to one.
An epistemic state is a global optimum relative to initial commitments if and only if the state maximizes for .8
Is a reflective equilibrium simply an optimal epistemic state in the sense just defined? The literature on RE suggests otherwise. Even an epistemic state that maximizes the achievement function may fall short of satisfying further requirements, or optimality conditions on epistemic states. The following such requirements are mentioned in the RE literature (see Elgin 1996: 103; 2017: Ch. 4; Baumberger & Brun 2016):
| CC | The commitments are fully consistent. |
| CCT | The theory and the commitments are consistent with each other (in the sense of being dialectically compatible; see App. A for this notion). |
| FA | The theory fully accounts for the commitments, i.e., it accounts for each commitment. |
| FEA | The theory fully and exclusively accounts for the commitments, i.e., the theory accounts for each commitment and nothing else. |
Note that all the requirements are related to our desideratum of account. This is obvious for FA and FEA. It is also clear for CC and CCT since a set of commitments that is inconsistent (with a theory) cannot be well accounted for by theories, which are consistent by definition.
Against the background of these different additional requirements, we distinguish, all in all, two notions of an epistemic state being in reflective equilibrium.
| 1. | A state is called a RE state (relative to initial commitments ) iff (1) it is a global optimum according to the achievement function , and (2) the theory and the commitments are jointly consistent (CCT). |
| 2. | A state is called a full RE state (relative to initial commitments ) iff (1) it is a global optimum according to the achievement function and (2) the theory fully and exclusively accounts for the commitments (FEA). |
2.3. The Process of Equilibration
Canonical descriptions of RE, e.g., in Goodman (1999), include a specification of a process in which commitments and principles are successively revised and step-wise adjusted to each other. In our model, this process of equilibration starts from an initial epistemic state, to which two adjustment rules—revision of theory and revision of commitments—are iteratively applied, until a stopping condition is satisfied.
Initial Epistemic State:
The agent starts with a set of initial commitments ; to simplify matters, we can assume that she starts with an arbitrary theory.
Revision of Theory:
Given her current commitments , the agent searches for a systematic theory that accounts for her commitments. More precisely, the agent newly adopts an epistemic state such that the theory scores best in terms of the achievement function given . Since the current commitments are fixed, faithfulness does not effectively make a difference, as it does not depend on the theory.
Revision of Commitments:
Given her current theory , the agent adjusts her commitments to the theory, while moving not too far from the initial commitments. More specifically, the agent replaces her current commitments with those commitments that score best on the achievement function (given ). Since the current theory is fixed, systematicity does not effectively make any difference, as it does not depend on the set of commitments.
Stopping Condition:
The two previously stated adjustment rules, revision of theory and revision of commitments, are consecutively applied until the application of both rules triggers no further changes, and the agent’s epistemic state stabilizes: . That is, the process of equilibration ends if a fixed point is reached.
2.4. Convergence and Epistemic Progress in the Model
We close the description of the formal model of RE by stating some of its more or less straightforward properties (proofs are provided in Appendix B).
| 1. | Equilibration processes always lead to progress; at least, they do not make things worse. More precisely, the epistemic value of a state, as measured by the achievement function, is at least as great as the epistemic value of all previous states. In particular, the equilibration fixed point displays strictly greater epistemic value than the initial state, provided the two are not identical. |
| 2. | Equilibration processes always end at a fixed point. In a nutshell, this is because we have a finite set of epistemic states and the achievement function increases monotonically during equilibration processes (see item 1). |
| 3. | For every global optimum (and hence for every full RE state) there is a set of initial commitments and an equilibration process that leads from the initial commitments to the global optimum. |
| 4. | For extreme parameter choices (i.e., or ), every equilibration fixed point is a global optimum. |
| 5. | If each combination of weights from a set yields the same set of global optima (the same unique equilibration process with no random choices) for a fixed dialectical structure and fixed initial commitments, then every combination of weights in the convex hull of yields the same set of global optima (resp. the same equilibration process), too. |
3. A First Case for the Model: Illustrative Examples
So much for our model. But does it adequately represent the core of RE? This section unfolds a first case for a positive answer to this question. We argue that the model implies global optima and revision processes that can be intuitively recognized as RE states and equilibration processes, respectively. To this purpose, we take a simple dialectical structure and consider four sets of initial commitments. For each set of initial commitments, we determine the global optima and run a computer simulation (see Appendix A) of the equilibration process. We interpret the findings and show that our results can be understood as reasonable RE states and processes.
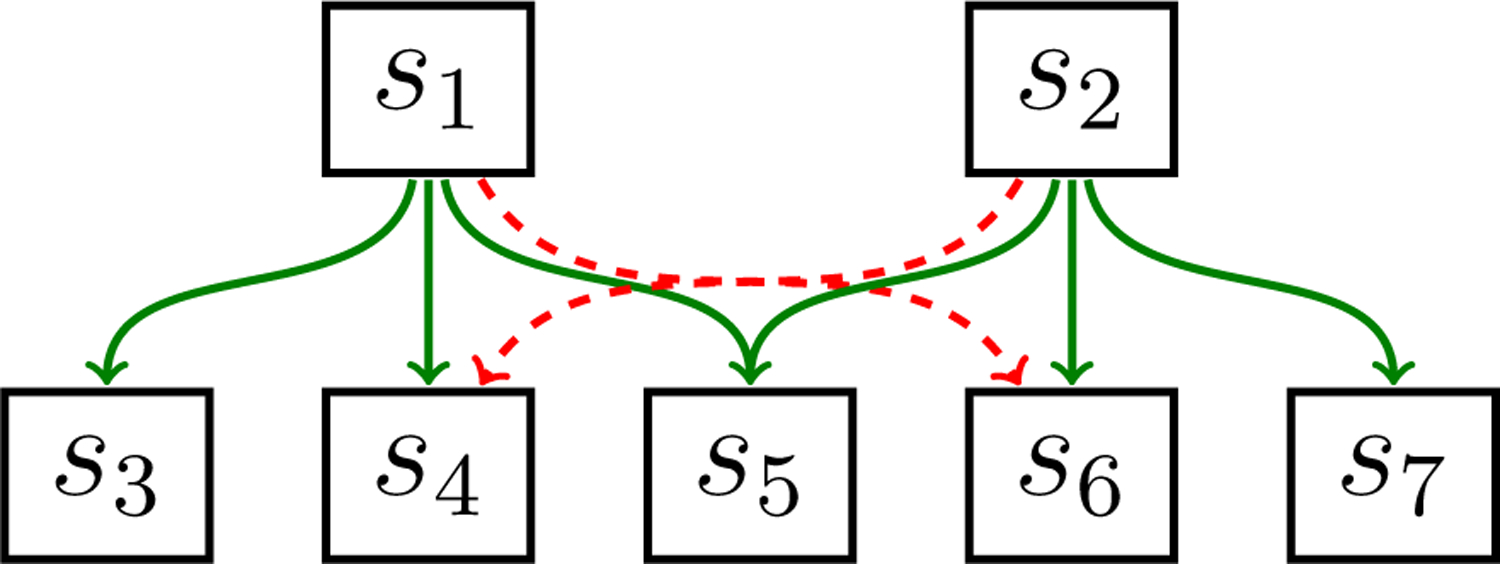
Our examples are based upon a topic that is characterized in terms of the sentences and their negations, which are inferentially related as follows: implies , , and , while implies , , and . The inferential relationships between the sentences are visualized in Fig. 1.
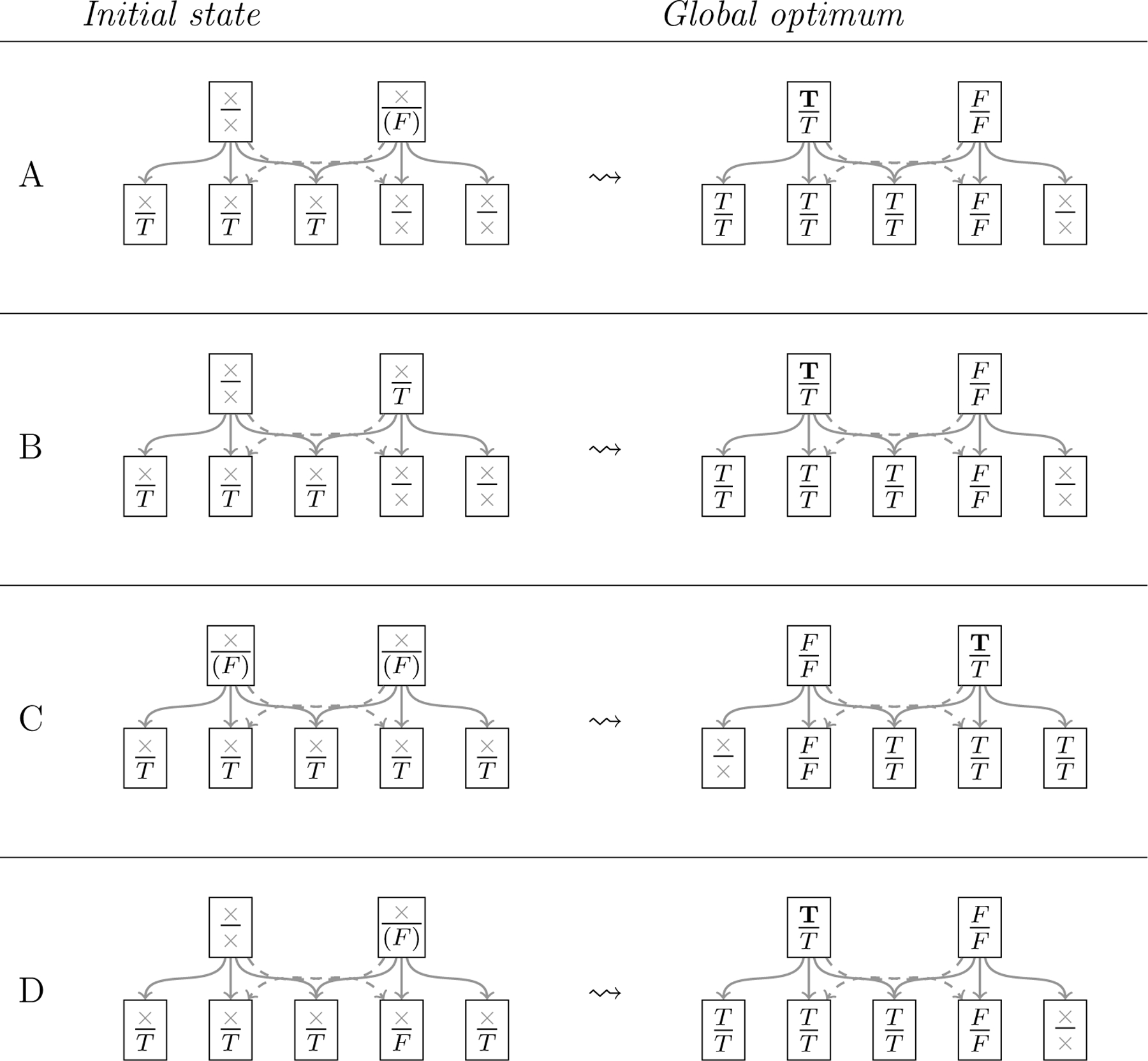
Each of our four examples, A, B, C, and D, is defined through specific initial commitments, namely ; ; ; and . We set our weights of the desiderata in the achievement function as follows: , and . (A robustness analysis shows that these specific weights lie within a larger region of the parameter space where identical simulation results are obtained. Only in case C, there are two global optima due to the symmetry, and which of them is reached by the equilibration depends on the random choices.)
Turn first to the global optima that correspond to the initial states. They are provided in Fig. 2.
Initial states and corresponding global optima for four equilibration processes. Epistemic states (theory plus commitments) are visualized by means of the standard inferential network (see Fig. 1). Each box, which represents a sentence, is divided by a horizontal line; the symbol at the top of the line describes the epistemic state’s theory, the symbol at the bottom the epistemic state’s commitments. “T”/“F”/“×” indicate that a sentence/its negation/neither belongs to a theory’s content or the commitments. Principles of a theory are set in bold letters. Bracketed symbols indicate the deductive implications of the commitments.
In case A, the agent holds initially three commitments, which are implied by , and one of which stands in contradiction to . These initial commitments are thus easily systematized by choosing as a principle. And indeed, the global optimum shown on the right-hand side of Fig. 2 includes a theory that has as its sole principle. Further, the commitments in the global optimum state perfectly match the content of the theory, so we have what we call a full RE state. Note that the commitments which are part of the optimum both include and extend those from the initial state. The commitments that are added are the principle of the theory , a consequence of the commitments and a consequence of the theory , respectively.
In case B, the initial commitments comprise those of case A plus sentence . The commitments are inconsistent because implies . Is the contradiction resolved in the global optimum? For this, either or needs to be given up. Now, , together with and can be easily systematized, as in case A, namely in terms of . The initial commitment , by contrast, does not easily lend itself to joint systematization with further commitments. This suggests that be dropped in the optimum. And this is indeed the case. The global optimum is the same as in case A; it is again a full RE state.9
In case C, the initial commitments are highly unsystematic (none implies another), yet consistent. A good part of the commitments can be systematized in terms of , while another part of them can be systematized in terms of . It is not possible to combine and in one theory because these sentences are inconsistent. A systematic theory contains either or . Due to the symmetry of the initial configuration, there are no reasons to prefer to , or to , and we expect the existence of two global optima. This is indeed the case; we show one of the optima in Fig. 2; the other one is the global optimum from cases A and B. Once again, the commitments in the optimum are fully accounted for, so we have full RE states.
In case D, the initial commitments resemble those of case C; however, the symmetry is broken by replacing with . Accordingly, the initial commitments contradict , but not ; thus, including in a theory does not look promising. The resulting global optimum conforms to this expectation. It is identical with the global optimum in cases A and B. It drops , which is not accounted for by the final theory, but otherwise embraces the initial commitments, which are now fully accounted for by a highly systematic theory. This final state is a full RE state once more.
In sum, the model results concerning global optima—understood in terms of RE—are highly plausible and in agreement with pre-theoretic intuitions. In particular, the global optima derived with the formal model seem epistemically superior to the initial states, which is especially evident in example B, in which a contradiction is resolved. Therefore, our model appears to provide an adequate representation of the axiological dimension of RE.
Let us now turn to the equilibration processes simulated by the model. Can the stepwise adjustments of epistemic states, derived with the model, be recognized as reasonable RE processes? In particular, do they lead to the corresponding global optima, and if so, how?
To answer these questions, we first take a closer look at the equilibration process in case C, which proceeds in six steps, as shown in Table 1. Let us interpret this process bit by bit. The first theory chosen, in step 1, consists of two principles, and . Here, accounts for through , while , as it were, accounts for itself. Due to a symmetry in the initial state, the set of principles would do equally well.10 In step 2, the commitments are adjusted in such a way that they coincide with the content of the principles. It is tempting to assume that we have now reached a fixed point, but this is not the case. If we remove from the principles of , we gain in systematicity and lose in account because the commitment is not accounted for anymore. At this point, systematicity tops account and is dropped as a principle in step 3.11 In step 4, is dropped as a commitment. This means, we (re-)gain in terms of account, but lose in terms of faithfulness. Yet, it is overall preferable to drop due to specific parameter settings (weights). After step 4, neither theory revision (step 5) nor commitment revision (step 6) yield any further changes. We have reached a fixed point. As noted above, this final state is a global optimum, albeit not the only one. Since the commitments and the content of the principles coincide, we have reached a full RE state.
Details of equilibration process in case C. The first row below the column header states the initial commitments, the following rows provide the newly revised theories/ commitments that result from the corresponding adjustment steps. Steps with an odd number revise a theory (as in Figure 2, principles are set bold). Steps with an even number adjust the commitments.
| step | result | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| (F) | (F) | T | T | T | T | T | |||
| 1 | F | T | T | F | T | T | T | ||
| 2 | F | T | T | F | T | T | T | ||
| 3 | F | T | F | T | T | T | |||
| 4 | F | T | F | T | T | T | |||
| 5 | F | T | F | T | T | T | |||
| 6 | F | T | F | T | T | T | |||
We obtain similar results for the other three examples (A, B and D): In each case, the process soon reaches a fixed point which coincides with the global optimum. This finding suggests that the equilibration process defined in our model is instrumental in pushing agents towards a full RE state. To further corroborate this conclusion, we have broadened the evidence base and simulated equilibration processes for two different random ensembles. The first ensemble is based on a random sample of initial conditions on the basic dialectical structure defined above. Using the same values of the weights as before, we find that in 95% of all cases, the equilibration fixed points are also global optima. Of these, 75% are full RE states. The second ensemble uses the initial commitments and dialectical structure from the four illustrative cases discussed above, but randomly varies the weights within the achievement function. Given such systematic parameter perturbation, 88% of the equilibration fixed points are also global optima; and of these, 65% are full RE states. These robustness analyses show that the process of equilibration as defined in the model is likely to lead to a global optimum or even a full RE state.
The reason why not all equilibration processes arrive at a global optimum is that the steps in the process only solve restricted optimization problems, while the optimization used for defining the achievement function is unrestricted. The reason why not all global optima are full RE states is that the achievement function balances account (a maximum amount of which is required for a full RE state) with other desiderata, e.g., simplicity. However, such limitations of the RE process dovetail with our pre-theoretic picture of RE, since we wouldn’t expect that every specific RE process leads to a globally optimal RE state.
All in all, the results we obtain when applying the model to various cases make sense with regard to both axiological (global optimum/RE state) and procedural dimensions (equilibration process). As it is evident from our examples, the global optima seem, intuitively, more justified than the corresponding initial commitments. In particular, an optimal epistemic state might resolve the inconsistencies contained in the initial state; its commitments are well accounted for by a few principles, and those initial commitments that are not well connected to the others are typically dropped in the global optimum. The simulated equilibration processes, too, can be plausibly understood as actual RE processes. That is because they often lead to a global optimum, are thus instrumentally valuable and give rise to epistemic progress. The processes implied by our model easily lend themselves to an interpretation in terms of RE. Therefore, the model, which gives rise to all these meaningful results, is itself an adequate representation of the core aspects of RE.
4. Discussion of the Model
It is now time to systematically assess our model by drawing on our requirements laid down in the introduction. To this effect, we first extend the case made in the previous section that the model adequately represents the core idea of RE (Sect. 4.1; cf. requirement (i)). This result allows us to use the model to draw conclusions about RE itself, and we also argue that it raises interesting questions about RE, which, in turn, can be answered using the model. Therefore the model is fruitful (Sect. 4.2; cf. requirement (ii)). We finally show that the abstractions and idealizations of the model do not undermine our findings (Sect. 4.3).
4.1. Representation of RE
Apart from the fact that the implications of the model, as exemplified in the last section, are plausible, there is an additional reason why our model adequately represents the core of RE, as it is characterized in previous work.
By design, the model structurally mimics elaborate informal accounts of RE (e.g., Baumberger & Brun 2016). In particular, the most important components included in these accounts are covered by our model, viz. commitments and theories. Further, the model features a process as it is often mentioned in the literature: The agent starts from initial commitments, tries to systematize them in terms of a theory, and moves to and fro between commitments and theory until, eventually, an equilibrium (fixed point) is reached. In this respect, our model improves upon previous attempts to model RE in the computer science literature (e.g., Yilmaz et al. 2017). Because the latter do not confront the commitments with a separate theory, they do not really capture the core of RE.
4.2. Fruitfulness of the Model
Our model is fruitful because it implies some insights about RE, but also because it raises novel questions, some of which can be addressed using the model.12 This subsection organizes the various reasons for why the model is fruitful in five items.
First of all, the model shows that RE allows for consistent specification. This follows from the fact that (1) our model adequately represents the core of RE and (2) that it has non-trivial solutions. This point is significant because the previous debates about RE may have let readers doubt whether there is more to RE than vague metaphors and mixed ideas that cannot be elaborated exactly and may even turn out to be inconsistent.
Second, our model incorporates a conceptual clarification: RE divides into (a) an axiology of epistemic states and (b) the dynamics of a process, during which epistemic states are changed according to rules. The axiology is included in the desiderata and the achievement function. It determines what counts as a (full) RE state. The dynamics are defined in terms of adjustment rules and a stopping condition. They describe how the epistemic agent should seek a (full) RE state. Although our model specifies the adjustment rules by referring to the achievement function, this is not necessary, and alternative adjustment rules may be provided. Thus, from a conceptual point of view, the process remains clearly distinguished from the axiology. Further, even in our model, equilibration may not lead to a global optimum concerning the achievement function.
From an epistemological point of view, this raises a fundamental question of normative priority. What does it take one to be justified in one’s view? Do we have to follow some rules regardless of where they lead us, as proceduralists would suggest? Or should we embrace consequentialism and hold that the rules are only instrumental in obtaining certain consequences, viz. states that are better in terms of desiderata which, in turn, are independent of, and prior to, the process? Or should we try to adopt a third, alternative stance that escapes this dichotomy (as Elgin 1996; 2017 argues)? So far, the literature about RE has not paid sufficient attention to the contrast between consequentialism and proceduralism, and specifically to the question of how the process of equilibration relates to RE as a target state (see Baumberger & Brun 2020 for a recent exception).
At first sight, understanding RE in consequentialist terms seems more plausible. For this reason, our take on RE in this paper was essentially consequentialist, e.g., when we argued that the process is plausible because it leads to progress as measured by the achievement function. Note, though, that the specific rules proposed in this paper may well be outranked by other rules that are more likely to lead to a global optimum, at least under certain circumstances. The question thus arises which set of rules is instrumentally most effective. This question can be answered using our model: We can assess alternative versions of equilibration procedures in terms of their success rate. Still, our model may also be used to study the alternatives to consequentialism. For instance, one might further expand and modify the model to show how the dichotomy between consequentialism and proceduralism can be overcome. To this effect, one might want to change the definitions of (full) RE states by adding requirements that depend on the process.
A third reason why our model is fruitful: To obtain a concrete model of RE, we had to set weights on the desiderata. Had we not done so, we would not have arrived at a systematic way to decide between them in cases of conflict. Nor could we have defined the achievement function and global optima. In a nutshell, no RE without trade-offs.
That different theoretical virtues may pull in different directions is, of course, common lore in philosophy of science, at least since Kuhn (1977). However, the existing literature about RE is largely silent about such trade-offs (exceptions include Baumberger & Brun 2016; 2020; Elgin 1996; 2017). Our model is thus fruitful because it raises the question how the weights should be set in RE. There are several possible strategies to answer this question. At one extreme, proponents of RE may claim that a particular choice of the trade-offs (or a small range of choices) is characteristic of RE. This would mean that the method of RE as such requires specific values of the weights , and . Since these weights haven’t been specified so far, our model may be used to determine values of the weights such that the results obtained for the global optima and the equilibration process are maximally plausible and in accordance with what proponents of RE have expected. An alternative is to claim that the weights depend on the topic and the context. At the other extreme, it may, finally, be suggested that RE doesn’t commit us to any specific choice concerning the tradeoffs. It would rather be at the discretion of the epistemic agent to set weights. An advantage of this strategy is that RE will then cover more processes in which agents change their view. From a third-person perspective, many such processes may be accommodated by fitting the values of the weights to the process. As a downside, RE wouldn’t provide very specific advice and may consequently seem quite arbitrary. This is not the place to discuss these strategies. Rather, our point is that our model is fruitful not just because it forces proponents of RE to think about the weights, but also because it allows the systematic investigation of different sets of weights and their consequences.
An immediate implication—and this is our fourth point—is that a lot of the discussion about RE has been premature. For instance, some authors, e.g. Brandt (1985), have argued that RE is too conservative. Is it? According to our model that depends on the values of the weights. Clearly, the method will be more conservative if faithfulness obtains more weight. Conversely, proponents of RE have argued that RE has all kinds of desirable features, for instance that it likely removes inconsistencies. Does it? The extent to which it does again depends on the weights. Our model can help to advance the discussion about these issues. We can use our model to systematically study the behavior under alternative sets of weights. A strong case for RE can be made if there is a set of weights such that the model behavior has a lot of desirable features, while at the same time evading objections.
More generally—and this is our fifth and final point—our model draws the attention to numerous relevant questions that were not considered before, but that may systematically be studied using the model. For instance, a question that came up when simulating the equilibration process is how frequently an agent faces epistemic ties and whether it is advisable to branch an equilibration process rather than resolving ties by chance. Another example of such a novel question concerns the degree of under-determination within RE: Global optima are not necessarily unique, and the model provides a framework to measure the extent of under-determination under different conditions of RE.
4.3. Limitations and Perspectives for Further Research
Models are often met with suspicion because of their idealizations and abstractions, which seem to impede any inference from the model to a target system. So is our model problematic in this regard? In what follows, we argue that this is not the case. For reasons of space, we only consider limitations that seem most salient and significant. We will show that they can be overcome either by re-interpreting or by de-idealizing the model.
Components of the Model.
Our model is quite parsimonious because it includes only two components: sets of commitments and theories. It is, therefore, a model of so-called narrow reflective equilibrium. By contrast, proponents of wide equilibrium suggest to additionally include background theories (see Daniels 1979: 258–64). Such background theories are typically held fixed during the RE process, but constrain the construction of a reflective equilibrium state.
There is, however, a way of re-interpreting our model as implicitly containing background theories. We may assume that the arguments from the dialectical structure comprise not just the valid arguments, but also the arguments that are valid given the relevant background theories. What we call consistency, then, is effectively consistency with the background theories, which means that background theories restrict the choice of theories. It would also be easy to model a background theory explicitly: In the dialectical structure, we may include a theory that is fixed and the consequences of which should not be contradicted by the commitments and/or the theory systematizing the former.
Commitments.
An obvious limitation of our model is that it does not include weights for the commitments. In a realistic application of RE, the agent may be more committed to some things rather than others, and she may draw on related weights when deciding which commitments should be given up in revision-of-commitments steps (see Goodman 1999: 64). However, weights which are taken into account in measuring account and faithfulness can be incorporated into the model straightforwardly. We have refrained from doing so to keep the number of degrees of freedom low.
Desiderata.
Another possible objection is that the model is too idealized as far as some of the desiderata are concerned.
For instance, in the model, the systematicity of a theory only depends on its simplicity, which, in turn, is just measured by counting the number of its principles. But in our reasoning practice, there is more to systematicity than simplicity of this sort. For example, a theory is also highly systematic if its principles allow for systematic classification, and the simplicity of a theory also depends on how complicated each of its principles are. In order to capture (1) the extent to which principles jointly allow for a systematic classification and (2) the extent to which they are individually simple, we would need to look at the principles’ formulation, which is neglected in our model so far, because each principle is represented by a sentence without any internal structure.
However, this is no principled problem for our approach as long as, in concrete applications, the sentence pool is appropriately chosen. For instance, if we include in the sentence pool atomic sentences that classify single items, then a systematic classification should show itself in the inferential structure because the classificatory principles imply the atomic sentences that do the classificatory work. As far as complicated principles are concerned, we can exclude them from the sentence pool. So by postulating certain requirements on the sentence pool, we can make sure that classification and the simplicity of single sentences play some role.
As far as account is concerned, the model assumes that principles account for a single commitment if and only if the principles entail the commitment. This condition on account is arguably too strong: A commitment may be accounted for because it follows from the principles in a non-deductive way, for instance using a statistical explanation (Hempel 1965: Sect. 3.3).
This limitation might be overcome by re-interpreting the arguments in our model and by allowing that they include inductive arguments. As a consequence, we would have to re-interpret our consistency as a sort of coherence. We leave the exploration of this to future work.
In a different perspective, our representation of account may seem too weak. If accounting for commitments is likened to explanation, which does not reduce to deductive inference, then our “inferentialist” definition of account is too liberal. What might be needed, additionally, are further restrictions on the arguments that constrain inference schemes or premises, e.g., that no grue-like predicates appear in the premises or that at least one of the premises is law-like (see Hempel & Oppenheim 1948 and Hempel 1965). Such requirements on the premises are not captured in the model.13
But this worry may again be alleviated by postulating that the sentences (or, more generally, the arguments) under consideration comply with certain requirements, e.g., that they do not contain grue-like predicates. Note also that explanatory power may be manifest in the inferential relationships, because explanatory hypotheses, according to certain unificationist accounts of explanation (see Friedman 1974; Kitcher 1989), typically have more consequences.14
RE Process.
Finally, our model of the process of equilibration may seem too idealized because the adjustment rules often lead to extensive revisions that are cognitively and computationally very demanding. For instance, in revision-of-theory steps, the epistemic agent has to identify the best theory from scratch. This requires her to consider all combinatorially possible consistent sets of sentences in the dialectical structure, and to identify their deductive closures. Likewise, in revision-of-commitments steps, the agent is supposed to go through all combinatorially possible sets of commitments to find the set which strikes the best balance between account and faithfulness. We thus seem to deviate from the “piecemeal” approach to equilibration often described in the literature on RE (paradigmatically in Goodman 1999: 64).
But this complaint only affects one part of the model, viz. the specification of the equilibration process, while the axiology is untouched. We can thus easily amend the rules without questioning the whole model. A very simple idea is, for instance, that, in revision-of-commitments steps, at most one commitment may be changed. But, of course, an entire spectrum of more elaborate options, e.g., to let weights of commitments determine revisions, wait for further investigation.
All in all, our model is subject to limitations, but they do not pose a serious threat, or so we have argued. Nor is the main result of our paper affected by these limitations. For, if the model can be re-interpreted or easily changed to avoid the potential shortcomings, then our claim that RE allows for consistent specification stands. In addition, the critical discussion further underpins that the model is fruitful (which is our second claim): By showing how current limitations can be overcome through further elaboration of the model, a systematic research program emerges.
5. Conclusions and Outlook
All too often, descriptions of RE strike readers as unspecific and metaphorical. As a result, the method is difficult to apply and debates about the merits and pitfalls of the method have remained inconclusive. This paper has tried to overcome this problematic state of affairs. We have shown that the core idea of RE can be consistently spelled out. To this purpose, we have developed a formal model of RE. The model is not only precise on what it means to mutually adjust a set of commitments and a theory, it is also fruitful because it opens new pathways into the study of RE.
The model focuses on narrow as opposed to wide RE. It distinguishes between two main components of an agent’s epistemic state: commitments and theories. Epistemic states are subject to three desiderata, viz. account, systematicity, and faithfulness, and further requirements. The desiderata and requirements first define what counts as an RE state—an ideal or target state. Second, the desiderata guide the agent through a process of equilibration during which the commitments and the theory are mutually adjusted.
Using computer simulations, we have shown that the model has plausible solutions. Since the model adequately represents the core of RE, this is a proof of concept of RE: the central idea behind RE can be spelled out consistently.
Our formal model of RE further clarifies the concept of RE. In particular, in our model, it can be shown that
| 1. | equilibration processes always end at a fixed point; |
| 2. | every full RE state can be reached by some equilibration process starting at some point. |
This is good news for proponents of RE. But there is also some work ahead for them. This is because the model highlights issues which have not sufficiently been dealt with in the existing literature or escaped it altogether: Under which conditions is the full RE state unique? How close do the fixed points come to full RE states, and how do they generally score regarding the epistemic desiderata? Are there sets of initial commitments that render it particularly difficult to make epistemic progress in terms of the desiderata? How does the trade-off between the desiderata impact on the full RE state and the equilibration process? How should the trade-off be set? And are there alternative—more effective, or computationally less demanding—rules for the equilibration process?
These questions, which are just the tip of the iceberg, can be addressed through formal modelling. The simple model of RE, presented in this paper, lays groundwork for novel and promising lines of research.
Acknowledgments
Earlier versions of this paper have been presented in Cracow, Erfurt, Düsseldorf, Prague, Munich, and Bern. We would like to thank the audiences and in particular Catherine Z. Elgin and Rainer Hegselmann. Thanks also to the anonymous reviewers. The research for this paper is part of the projects “Reflective Equilibrium – Reconception and Application” (Swiss National Science Foundation grant no. 150251) and “How far does Reflective Equilibrium Take us? Investigating the Power of a Philosophical Method” (Swiss National Science Foundation grant no. 182854 and German Research Foundation grant no. 412679086).
A. Formal Presentation of the Model
This appendix provides the technical details of the model. We draw on terminology and results from Betz (2010; 2012). The documented code used to run and analyse the computer simulations presented in this paper is available at https://github.com/debatelab/remoma.
A.1. The Conceptual Framework: Binary States on Finite Inferential Nets
The sentence pool represents natural-language sentences that are relevant to a topic. is closed under negation (i.e., , where we stipulate that ). Let .
Arguments describe the deductive inferential relations between the sentences in the sentence pool. An argument is defined as a pair consisting of premises and a conclusion . Let denote the set of all arguments. Sentence pool and arguments constitute a dialectical structure .
A position on a dialectical structure is simply a subset of , . Note that such a set may contain and for some . The domain of position is the set .
A position with domain is called
| • | complete iff , |
| • | partial iff . |
A position extends a position iff .
Positions are minimally consistent iff they don’t contain ‘flat’ contradictions, i.e., iff
A consistent position, besides being minimally consistent, takes into account the inferential relations between sentences that are established by the various arguments in the dialectical structure: A complete position on is consistent iff it is minimally consistent and
A partial position on is consistent iff there exists a complete and consistent position which extends .
The (dialectic) closure of a consistent position , symbolized by , is the inter-section of all consistent and complete positions which extend . Two positions , are dialectically compatible iff there exists a consistent and complete position which extends both.
A.2. Basic Components of RE
In modeling RE, we assume that the topic and the inferential relations, i.e., the dialectical structure , are given and fixed.
For every , the set of commitments of an agent, , is a minimally consistent position on .
A theory is a consistent position on . The sentences which belong to a theory are called its principles. The content of a theory, , is its (dialectic) closure .
A pair of commitments and theories, with or , is called the epistemic state of an agent.
A.3. Axiology: Desiderata, Global Optimum, and RE State
There are three desiderata on epistemic states: account, faithfulness, and systematicity. We consider them in turn.
A theory accounts for a single sentence iff (dialectically) entails , i.e. . It accounts for commitments to the extent to which the commitments, and only the commitments, belong to the theory’s content, . The degree to which accounts for , , is a monotonically decreasing function of the normalized weighted distance between and :
(1) where is a weighted Hamming Distance between arbitrary positions , ,
(2) with the penalty function ,
(3)
In our model, is chosen as
(4) Faithfulness, , measures the extent to which commitments are faithful to initial commitments, ; it is defined as
(5)
Faithfulness is defined in terms of the same Hamming Distance as account, with only one exception: There is no penalty if the commitments go beyond the initial commitments .
Systematicity, , of a non-empty theory is defined as an inverse function of the number of its principles, normalized by the size of its content, that is
(6) in addition, we set
The achievement function, , is a convex combination of these desiderata.
(7) where the weights , , are non-negative real numbers that add up to 1. The achievement function expresses the overall degree to which an epistemic state satisfies a specific trade-off between the desiderata according to the choice of the parameters , , .
A.4. Dynamic Aspects: Equilibration Process
The equilibration process starts from a given initial epistemic state (A), which is modified by revising, individually and iteratively, theories (B) and commitments (C), until no further improvements are available (D).
| A. | set initial epistemic state , where is given as input and is arbitrary. |
| B. | Revision of theory: Choose new theory : is chosen from all consistent positions such that is maximal; if several such maxima exist and is among them, ; if several such maxima exist and is not among them, is a randomly drawn maximum. |
| C. | Revision of commitments: Choose new commitments in view of and initial commitments: is chosen from all minimally consistent positions such that is maximal; if several such maxima exist and is among them, ; if several such maxima exist and is not among them, is a randomly drawn maximum. |
| D. | Stopping rule: stop if , else set and goto B. |
B. Proofs: Convergence and Epistemic Progress
Proposition 1.
The epistemic value of a state, as measured by the achievement function, is at least as great as the epistemic value of all previous states. In particular, the equilibration fixed point displays strictly greater epistemic value than the initial state, provided the two are not identical.
Proof: By definition of revision of theory and revision of commitments, we have for every , and we have equality iff , respectively . So, for every with and (and in particular for a fixed point of this kind), is strictly greater than .
Proposition 2.
Equilibration processes always end at a fixed point.
Proof: Because the sentence-pool is finite, the state space of the equilibration process is finite, too. So any series of epistemic states generated through equilibration either leads to a fixed point or exhibits a cycle. We show, by indirect proof, that the latter scenario is impossible. So let’s assume for the sake of the argument that there’s a cycle, i.e., there exist , with such that . This means that . But this entails (again, with Proposition 1) that is a fixed point and that the equilibration process would have stopped no later than at step , without giving rise to the cycle.
Proposition 3.
For every global optimum (and hence for every full RE state) there is a set of initial commitments and an equilibration process that leads from the initial commitments to the global optimum.
Proof: Let be a global optimum. Consider an equilibration process that starts with initial commitments . If is a unique global optimum, theory revision will pick immediately , and a fixed point is reached. If, in contrast, there exists such that is a global optimum, too, the probability that theory revision picks is greater than zero and smaller than 1—so it is possible that the global optimum is reached.
Proposition 4.
For extreme parameter choices (i.e., or ), every equilibration fixed point is a global optimum.
Proof: Let, first, . Then the achievement function is simply the account function . Theory revision will first pick the theory that best accounts for (if is consistent, then ). Next, commitment revision takes as new commitments. is a global optimum and also a fixed point. Consider, second, . We divide this case in three subcases: ; (ii) ; and (iii) neither (i) nor (ii). In subcases (i) and (ii), boils down to and , respectively. In subcase (i), the initial epistemic state is, therefore, both fixed point and global optimum. In subcase (ii), theory revision picks a theory which is maximally systematic, and commitment revision retains because there are no other commitments that would increase ; is not altered anymore and optimizes . Finally, in case (iii), theory revision picks a theory which is maximally systematic, and commitment revision maximizes faithfulness and hence retains . is the fixed point reached. It is also a global optimum with respect to because an item that maximizes a function and a function also maximizes any convex combination of and . □
Proposition 5.
If each combination of weights from yields the same set of global optima (the same unique equilibration process with no random choices) for a fixed dialectical structure and fixed initial commitments, then every combination of weights in the convex hull of the set yields the same set of global optima (resp. the same equilibration process), too.
Proof: It suffices to consider the case ; iterating the same proof then yields the proposition. So, we consider two sets of weights and as well as an arbitrary linear combination thereof, i.e., for a . Here, we can take the to be three-dimensional vectors; equivalently, we can say that the combination is a point on the line between the points corresponding to the points in a ternary plot. With arbitrary dialectical structure and initial commitments given and fixed, let us refer to the RE model specifications with the corresponding weights as specifications , and . This said, we need to prove:
| (a) | If the specifications and exhibit the same set of global optima, so does . |
| (b) | If the specifications and give rise to the same equilibration process without any random choice, so does . |
Now, the global optima referred to in (a) are determined by unrestricted maximization of the corresponding achievement functions, call them , , and . “Unrestricted” means that the maxima of the achievement function are determined within all epistemic states. The equilibration processes referred to in (b), by contrast, consist in a series of restricted maximizations of the achievement function. In every equilibration step, the achievement function is maximized on the set of epistemic states with either the theory or the set of commitments held fixed. Two equilibration processes are identical if and only if the consecutive restricted maximizations lead to the same maximum in each and every step. (By assumption, the maxima in these steps are unique, cf. “with no random choices.”) But all this means that both (a) and (b) follow from
| (c) | For all sets , of epistemic states: If is the set of maxima for specifications and on , then is also the set of maxima for specification on . |
As the model specifications , and only disagree in terms of their respective achievement functions , , and , (c) boils down to:
| (d) | For all sets , of epistemic states: If is the set of maxima of and of on , then is the set of maxima of on . |
To prove statement (d), we assume and to be given in accordance with (d)’s antecedent conditions. Moreover, it is easily verified that
(8)
The remaining proof proceeds in two steps. We first show that every epistemic state in is a maximum of on . Second, we prove that, vice versa, every maximum of on belongs to .
Suppose first that belongs to , i.e., maximizes the achievement functions and on . Thus, for all in :
(9) for . Consequently, for all in :
(10) By (8), this is to say that is also a maximum with respect to the achievement function on . Thus, every that maximizes both and also maxmizes .
Assume, conversely, that maximizes in . Assume for a proof by contradiction that it doesn’t maximize (the case of can be treated in an analogous way). Then there is a maximum with respect to such that
(11)
Since and have the same maxima, we have also
(12)
Thus—again by (8)—
(13) which contradicts the maximality of C, T regarding . This means that does not have maxima over and above the ones for and . □
Notes
- In fact, several inferential relations, given contraposition. ⮭
- It is sometimes assumed that the commitments entering RE always refer to particular cases. This would be problematic, since people are not only committed to judgments about particular cases (Rawls 1975). ⮭
- A note on terminology: Properly speaking, a set of sentences represents a set of commitments. But for simplicity of expression, we will sometimes identify a set of commitments with the corresponding set of sentences. Analogous points apply to other components of RE. ⮭
- We prefer the term “account” because the relation of something accounting for something else is not symmetric and thus stresses that theories and commitments play different roles. ⮭
- See Sect. 3, case C; see also App. A for details. ⮭
- Note, as a reply to an obvious objection: If the set of sentences SP is not closed under conjunction, then it may not be possible to conjoin several principles in one sentence. So one cannot trivially axiomatize every theory in terms of a single principle. ⮭
- This desideratum may be motivated in two ways (Baumberger & Brun 2020): (1) The initial commitments have initial credibility/tenability, which contributes to the justification of the resulting commitments (see Elgin 1996: 100–7; 2017: 66–67, 85); (2) The initial commitments determine a topic that should not be given up by moving too far from the content of the initial commitments (Elgin 2017: 66; Baumberger & Brun 2016: Sect. 4.5). ⮭
- If the sentence pool, SP, is finite, as we shall assume in what follows, there is at least one such global optimum. ⮭
- Note that being a global optimum (regarding the achievement function) in one case doesn’t imply being a global optimum in another case, because the achievement function incorporates faithfulness to initial commitments and may hence vary from case to case. ⮭
- Whenever we have such a tie, the equilibration process proceeds by making a random choice between the optimal options, see the formal model description in the Appendix. ⮭
- Note that the choice of the theory in step 1 faced a similar trade-off. To decide between and at step 1, the agent had to strike a balance between account and systematicity too. The only difference was that, at this stage, the theories under comparison did not account as well for the commitments as they do during step 3, where e.g., is part of the commitments. With our measure for account, differences in accounting for single commitments are more important in cases with a low degree of account than in cases with better account. The idea is that small deviations from full account make almost no difference, while they do matter in cases where we already observe pronounced failures to account for the commitments. Thus, at step 1, effectively, account is more important, and theory is best; while, at step 2, systematicity is more important, and theory prevails. ⮭
- We do, of course, not claim that the potential insights mentioned below are exclusive to our model—they may be reached by other clarificatory work on RE, too. ⮭
- The DN-model of explanation also requires truth, but this is not an issue here because we are only interested in possible explanations. ⮭
- Explanatory power is a theoretical virtue. We here discuss it in relation to account, the idea being that account covers this theoretical virtue. Alternatively, explanatory power may be conceptualized as a separate epistemic/pragmatic goal (cf. Baumberger & Brun 2016; Elgin 1996; 2017). ⮭
References
Baumberger, Christoph and Georg Brun (2016). Dimensions of Objectual Understanding. In Stephen Grimm, Christoph Baumberger, and Sabine Ammon (Eds.), Explaining Understanding: New Perspectives from Epistemology and Philosophy of Science (165–89). Routledge.
Baumberger, Christoph and Georg Brun (2020). Reflective Equilibrium and Understanding. Synthese. https://doi.org/10.1007/s11229-020-02556-9https://doi.org/10.1007/s11229-020-02556-9
Beauchamp, Tom L. and James F. Childress (2013). Principles of Biomedical Ethics (7th ed.). Oxford University Press.
Betz, Gregor (2010). Theorie dialektischer Strukturen. Klostermann.
Betz, Gregor (2012). Debate Dynamics: How Controversy Improves Our Beliefs. Springer.
Bonevac, Daniel (2004). Reflection without Equilibrium. Journal of Philosophy, 101(7), 363–88.
Brandt, Richard B. (1985). The Concept of Rational Belief. The Monist, 68(1), 3–23.
Brun, Georg (2014). Reflective Equilibrium Without Intuitions? Ethical Theory and Moral Practice, 17(2), 237–52.
Cohen, L. Jonathan (1981). Can Human Irrationality Be Experimentally Demonstrated? Behavioral and Brain Sciences, 4(3), 317–31.
Daniels, Norman (1979). Wide Reflective Equilibrium and Theory Acceptance in Ethics. Journal of Philosophy, 76(5), 256–82. Reprinted in Daniels (1996), 21–46.
Daniels, Norman (1996). Justice and Justification. Reflective Equilibrium in Theory and Practice. Cambridge University Press.
DePaul, Michael R. (2011). Methodological Issues: Reflective Equilibrium. In Christian Miller (Ed.), The Continuum Companion to Ethics (lxxv–cv). Continuum.
DePaul, Michael R. (1993). Balance and Refinement: Beyond Coherence Methods of Moral Inquiry. Routledge.
Elgin, Catherine Z. (1996). Considered Judgment. Princeton University Press, Princeton.
Elgin, Catherine Z. (2017). True Enough. MIT Press.
Foley, Richard (1992). Working Without a Net: A Study of Egocentric Epistemology. Oxford University Press.
Friedman, Michael (1974). Explanation and Scientific Understanding. Journal of Philosophy, 7191), 5–19.
Goodman, Nelson (1999). Fact, Fiction, and Forecast (4th ed.). Harvard University Press.
Hempel, Carl G. (1965). Aspects of Scientific Explanation. In Aspects of Scientific Explanation and Other Essays in the Philosophy of Science (331–496). The Free Press.
Hempel, Carl G. and Paul Oppenheim (1948). Studies in the Logic of Explanation. Philosophy of Science, 15(2), 135–75.
Keefe, Rosanna (2000). Theories of Vagueness. Cambridge University Press.
Kelly, Thomas and Sarah McGrath (2010). Is Reflective Equilibrium Enough? Philosophical Perspectives, 24(1), 325–59.
Kitcher, Philip (1989). Explanatory Unification and the Causal Structure of the World. In Philip Kitcher and Wesley C. Salmon (Eds.), Scientific Explanation (410–505). University of Minnesota Press.
Kuhn, Thomas S. (1977). The Essential Tension: Selected Studies in Scientific Tradition and Change. University of Chicago Press.
Lewis, David (1983). Philosophical Papers (Vol. 1). Oxford University Press.
Mikhail, John (2011). Elements of Moral Cognition: Rawls’ Linguistic Analogy and the Cognitive Science of Moral and Legal Judgment. Cambridge University Press.
Peregrin, Jaroslav and Vladimír Svoboda (2017). Reflective Equilibrium and the Principles of Logical Analysis: Understanding the Laws of Logic. Routledge.
Rawls, John (1999). A Theory of Justice (rev. ed.). Harvard University Press.
Rawls, John (1975). The Independence of Moral Theory. Proceedings and Addresses of the American Philosophical Association, 48, 5–22.
Resnik, Michael D. (1985). Logic: Normative or Descriptive? The Ethics of Belief or a Branch of Psychology? Philosophy of Science, 52(2), 221–38.
Resnik, Michael D. (1996). Ought There to Be But One Logic? In B. J. Copeland (Ed.), Logic and Reality: Essays on the Legacy of Arthur Prior (489–517). Oxford University Press.
Resnik, Michael D. (1997). Mathematics as a Science of Patterns. Oxford University Press.
Resnik, Michael D. (2004). Revising Logic. In Graham Priest, J. C. Beall, and Bradley Armour-Garb (Eds.), The Law of Non-Contradiction: New Philosophical Essays (178–94). Clarendon Press.
Shapiro, Stewart (2000). The Status of Logic. In Paul Boghossian and Christopher Peacocke (Eds.), New Essays on the A Priori (333–68). Oxford University Press.
Singer, Peter (2005). Ethics and Intuitions. The Journal of Ethics, 9(3–4), 331–52.
Stein, Edward (1996). Without Good Reason: The Rationality Debate in Philosophy and Cognitive Science. Clarendon Press.
Swanton, Christine (1992). Freedom: A Coherence Theory. Hackett.
Tersman, Folke (1993). Reflective Equilibrium: An Essay in Moral Epistemology. Almqvist and Wiksell.
Tersman, Folke (2018). Recent Work on Reflective Equilibrium and Method in Ethics. Philosophy Compass, 13(6), e12493.
Thagard, Paul (2000). Coherence in Thought and Action. MIT Press.
Thomson, Judith J. (2008). Turning the Trolley. Philosophy & Public Affairs, 36(4), 359–74.
van der Burg, Wibren and Theodoor van Willigenburg (Eds.) (1998). Reflective Equilibrium: Essays in Honour of Robert Heeger. Kluwer.
Williamson, Timothy (2007). The Philosophy of Philosophy. Wiley-Blackwell.
Yilmaz, Levent, Ana Franco-Watkins, and Timothy S. Kroecker (2017). Computational Models of Ethical Decision-Making: A Coherence-Driven Reflective Equilibrium Model. Cognitive Systems Research, 46, 61–74.