Suppositions—i.e. propositions that are provisionally accepted for the sake of argument—afford us a distinctive set of tools for deliberation. We use these tools to guide activities that are essential to intelligent behaviour, such as making predictions, forming plans, regretting past decisions, and determining our preferences about possible consequences of our actions. Bertrand Russell even once wrote that without supposition “inference would be inexplicable” (1904: 343).
Legend has it that suppositions come in two basic modes corresponding to whether they are introduced using the indicative or subjunctive grammatical mood. When a supposition is introduced in the indicative, subsequent propositions are to be assessed relative to what we would expect upon learning that the supposition were true. When one is introduced in the subjunctive, however, these evaluations should align with our judgments about how things would be if the supposition were in fact true (independent of whether we were aware of it). But suppositional judgments may be partitioned along a different axis. In some suppositional contexts, we offer coarse-grained qualitative judgments about whether a given proposition is acceptable. In others, we give finer-grained quantitative judgments reflecting how acceptable we find various propositions. In sum, this leaves us with four types of suppositional judgments to accommodate, which are reflected in the four varieties of normative theories of suppositional judgement that have been developed:
qualitative indicative theories,
qualitative subjunctive theories,
quantitative indicative theories, and
quantitative subjunctive theories.
Where (a) and (b) respectively specify norms for qualitative judgments under indicative and subjunctive suppositions, (c) and (d) respectively offer norms governing quantitative judgments under indicative and subjunctive suppositions.
The primary purpose of this paper is to shed light on the structure of these four varieties of normative theories of supposition by systematically explicating the relationships between canonical representatives of each. We approach this project by treating supposition as a form of ‘provisional belief revision’ in which a person temporarily accepts the supposition as true and makes some appropriate changes to her other opinions so as to accommodate their supposition. The idea is that our suppositional judgments are supposed to reflect our judgments about how things would be in some hypothetical state of affairs satisfying the supposition. Following this approach, theories of supposition are formalised in terms of functions mapping some representation of the agent’s epistemic state along with a supposition to a hypothetical epistemic state representing their suppositional judgments.
Theories of indicative and subjunctive supposition are thus characterised using different functions, while qualitative and quantitative theories differ in their respective representation of epistemic states. Qualitative approaches are articulated in terms of coarse-grained full/categorical/outright belief, while quantitative ones rely on finer-grained partial beliefs represented by numerical credences. As we will look at both types of theories, our agents’ epistemic states will consist of both qualitative beliefs and numerical credences.
To represent qualitative and quantitative attitudes, we start with a set of possible worlds and an agenda comprising an algebra of subsets of corresponding to propositions expressible in the finite propositional language . An agent’s beliefs will then be represented by a corpus comprising the set containing each proposition believed by the agent. Let denote the set of all possible corpora so that . Thus, qualitative suppositional theories can be characterised using a belief change operation, , which offers a functional mapping from each corpus and proposition to the set consisting of the propositions that are acceptable for such an agent under the supposition that . In similar fashion, an agent’s credences will be represented by a credence function satisfying the Kolmogorov axioms of probability. Letting will denote the set of all probability functions over , a quantitative suppositional theory is characterised by a credal update function . So, specifies numerical representations of how acceptable each proposition in the agenda is under the supposition for an agent with credences . When convenient, we will abuse our formalism by confusing sentences with their truth-sets . We also introduce analogous notation for sets of sentences , by defining .1 With this minimal formalism in hand, we turn to introduce our four representative theories depicted in table 1 below.
Four Theories of Supposition.
| Judgment | |||
|---|---|---|---|
| Qualitative | Quantitative | ||
| Supposition | Indicative | AGM Revision: | Conditionalization: |
| Subjunctive | KM Update: | Imaging: | |
Our representative qualitative indicative theory is given by the postulates describing AGM revision operations ( ) that were introduced by Carlos Alchourrón, Peter Gärdenfors, and David Makinson in their seminal (1985) work.2 For our qualitative subjunctive theory, we will consider the KM update operations ( ) characterised by the postulates proposed by Katsuno and Mendelzon (1992).3 The need to distinguish between these two was first proposed by Keller and Winslett Wilkins (1985), who suggested that “knowledge-adding” revisions are appropriate when new information is acquired about a static world, while “change-recording” updates are appropriate when learning that the world has changed in some way.4 Interestingly, both revision and update can be characterised as making the minimal change to the agent’s corpus needed to consistently accommodate new information. However, each relies on a different understanding of ‘minimal change’. For revision, we rely on a ‘global’ interpretation of minimality on which minimal change returns a corpus whose overall structure is as similar as possible to that of the original belief set; for update, we use a ‘local’ interpretation on which minimal change is achieved by applying local operations to the possible worlds that are consistent with the original corpus and thereby constructing the new corpus from the worlds yielded by those operations.
Our representative quantitative indicative theory is given by the familiar Bayesian rule of conditionalization, where represents the judgments that an agent with credences should hold under the indicative supposition . Lastly, our quantitative subjunctive theory will be given by the imaging rule introduced by Lewis (1976), where the credences that result from imaging under , , represent the judgments she should hold under the subjunctive supposition . There are some deep parallels between, on the one hand, the relationship between conditionalization and imaging and, on the other, the relationship between revision and update. Conditionalization (like revision) can be understood in terms of minimal change using a global interpretation of minimality. Conditionalization returns the globally most similar credence function that represents the new information as certain. Similarly, imaging (like update) can be treated in terms of minimal change using a local interpretation of minimality. Imaging shifts the probability mass from each world that is inconsistent with the new information to the locally most similar world that is consistent with it.
These similarities have not been overlooked. In their seminal paper axiomatising the update operation, Katsuno and Mendelzon explain that imaging can be seen “as a probabilistic version of update, and conditionalization as a probabilistic version of revision” (1992: 184). Similar claims are echoed throughout the literature. Despite the prevalence of such remarks, we are unaware of any attempts to systematically investigate how this plays out at the operational level. One way to understand the purpose of this paper is as an effort to make this claim precise and systematically explicate in what sense, if any, it is actually true. We find that conditions can be imposed that render the judgments made by the two indicative/subjunctive theories coherent with one another but there do not appear to be such conditions available that render coherence between the indicative/subjunctive and subjunctive/indicative theories. This, we argue, vindicates claims of the parallels between the qualitative and quantitative theories.
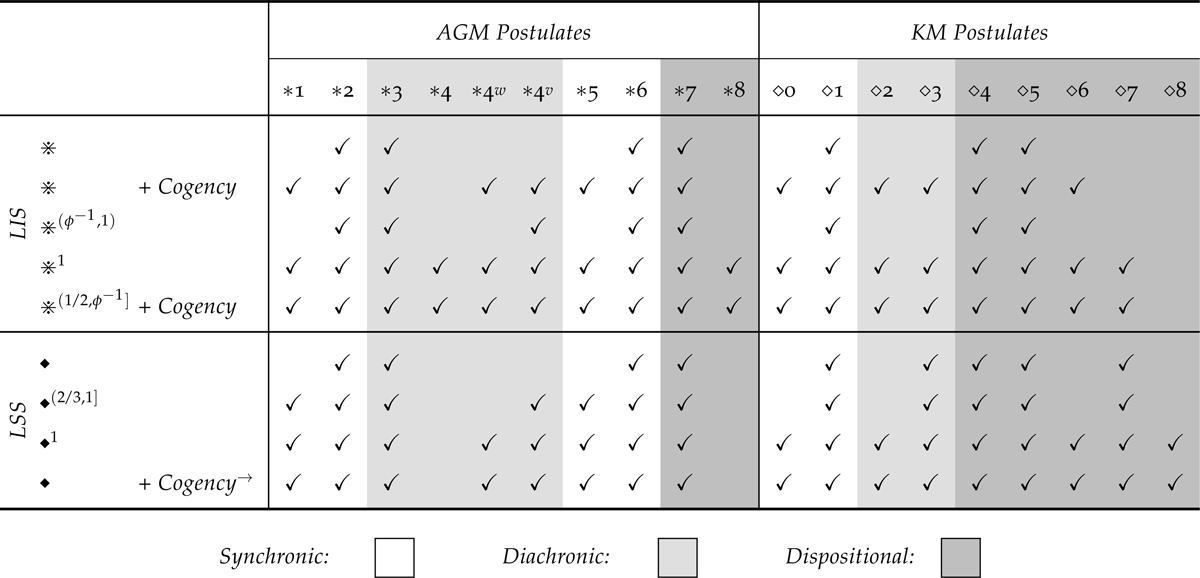
We proceed as follows: Section 1 briefly sets the stage with further discussion of the distinction between indicative and subjunctive supposition. Section 2 introduces our representative quantitative accounts and explains our method for comparing their recommendations with those provided by qualitative theories. In Section 3, we compare the theories of indicative supposition listed on the first row of table 1, AGM and conditionalization, by drawing on (and extending) results established by Shear and Fitelson (2019). In Section 4, we turn to the theories of subjunctive supposition from the second row of the table, KM and imaging, and systematically taxonomise the conditions under which they cohere with one another. Section 5 then addresses the remaining two diagonal comparisons suggested by table 1 (LIS vs. KM and LSS vs. AGM). Finally, Section 6 summarises the key findings of the analysis and outlines some prospects and remaining issues for future work. A summary of all results from this paper is provided in an appendix.
1. Two Modes of Supposition
On the standard story, the grammatical distinction between the indicative and subjunctive moods in a supposition aligns with a semantic difference between ‘epistemic’ or ‘ontic’ shifts in the modal base used for subsequent evaluations.5
In ordinary (non-suppositional) contexts, we assess propositions by the lights of our current opinions. In general, once we have supposed that for the sake of argument, we are to temporarily shift those opinions to match some hypothetical alternative epistemic state that represents as true. When the supposition is offered in the indicative mood, that shift is epistemic in the sense that it accords with the change of opinions that we would have undergone upon simply learning . Contrastively, when put forth in the subjunctive mood, the shift of our opinions is ontic, since we are to adopt opinions that coincide with those that we would come to hold if we were to learn that had suddenly been made true by some ‘local miracle’ or ‘ideal intervention’.
To see how this works, it will be instructive to look at an example. Adapting the classic case from Ernest Adams (1970), consider the indicative supposition in 1 and the subjunctive supposition 2 along with the propositions expressed by 3 and 4:
Suppose that Oswald didn’t shoot Kennedy. . .
Suppose that Oswald hadn’t shot Kennedy. . .
Someone else shot Kennedy.
Kennedy would have left Dallas unharmed.
Provided the indicative supposition in 1, the proposition expressed by 3 will no doubt seem acceptable. This is because learning that Oswald did not shoot Kennedy would not lead any reasonable person to give up the belief that Kennedy was shot; instead, the natural inference is to conclude that someone else was the assassin. In contrast, given the subjunctive supposition in 2, 4 seems appropriate. Here, we are to assess propositions relative to the most similar counterfactual world to the actual one in which Kennedy was never shot by Oswald. Since a world in which Oswald took but missed his shot is more similar to the actual one than one in which there was a second shooter, we judge that 4 is acceptable.
This clearly illustrates that the way in which rational agents adjust their epistemic states upon indicatively supposing a proposition will generally be radically different to the way in which they adjust those states upon supposing the same proposition in the subjunctive mood. We turn now to introducing the most salient quantitative theories for how one should adjust their judgments under indicative and subjunctive suppositions.
2. From Quantitative to Lockean Theories of Supposition
2.1. Quantitative Theories of Supposition
Bayesian conditionalization is most commonly understood as a diachronic norm governing the update of probabilistic credence functions. Under that interpretation, when an agent with a prior credence function learns that some event has occurred, she should adopt the posterior matching conditioned on so that for all . Conditionalization is defined as follows.
Conditionalization: Given a credence function and any with , conditioning by results in the credence function defined below.
Given the Bayesian understanding of conditionalization as an account of learning, and the close relationship between rational learning and indicative supposition, it is no surprise that conditionalization has also been understood as a normative quantitative model of indicative supposition. Interestingly, such an interpretation was first suggested by Rev. Thomas Bayes, who wrote, “The probability that two subsequent events will both happen is compounded of the probability of the first and the probability of the second on the supposition the first happens” (1763: 379). There are also more recent examples of this interpretation in the literature. For instance, this interpretation is explicitly endorsed by evidential decision theorists in their account of ex ante evaluations of option-outcomes.
The most popular alternative to evidential decision theory—causal decision theory—replaces the use of indicative suppositions in the calculation with subjunctive suppositions. The debate between evidentialists and causalists in decision theory boils down to a dispute about which type of supposition is relevant for ex ante evaluations of options.6 The standard treatments of quantitative subjunctive supposition derive from the imaging rule mentioned in the previous section. Although a number of different versions of imaging have been developed in the literature, we will focus on its best known (and simplest) version, first proposed by Lewis. On an intuitive level, the difference between conditionalization and imaging can be understood in terms of the type of minimal change they encode. We mentioned earlier that conditionalization relies on a global measure of similarity, where imaging uses a local one. This point is elegantly explained by Lewis:
Imaging on gives a minimal revision in this sense: unlike all other revisions of to make certain, it involves no gratuitous movement of probability from worlds to dissimilar worlds. Conditionalizing on gives a minimal revision in this different sense: unlike any other revisions of to make certain, it does not distort the profile of probability ratios, equalities, and inequalities among sentences that imply . (1976: 311)
To introduce the details of imaging, we will need to impose some extra structure on the space of possible worlds. Specifically, we assume that, for any proposition and possible world , there is a unique “closest” world at which the sentence is true. This notion is captured by using a selection function, . Intuitively, picks out the “closest” or “most similar” possible world to that satisfies . Our selection function will be subject to two basic conditions.
Centering: If , then .
This first condition requires that each world is the unique closest world to itself, i.e. if is true at , then there is no closer world where is true.
Uniformity: If and , then .
This second condition says that whenever the closest -world satisfies and the closest -world satisfies , they are one and the same. In order to illustrate the conceptual motivation for this constraint, we will take a brief but necessary detour into an important philosophical application of selection functions—namely, the semantics of subjunctive conditionals.
Under what conditions are subjunctive conditionals such as ‘If Richard Nixon had pressed the button, there would have been a nuclear war’ true? According to the proposal by Stalnaker (1968), this question is best answered in a semantics that utilises selection functions of the kind described above. The idea, roughly put, is that the subjunctive conditional in the example above is true just in case the closest possible world in which Richard Nixon did push the button is one where there was a nuclear war. The suggestion is that the truth value of the subjunctive conditional ‘if were true, would be true’ at a world is given by the following definition:
Stalnaker conditional ( ): The truth-conditions for the Stalnaker conditional, , are given by the semantic clause below.
As should be clear from its definition, the Stalnaker conditional is non-truth functional, since the truth-value of at a world does not supervene on the truth-values of its components at . Rather, it is true at just in case the closest world to at which its antecedent is true is also one at which its consequent is true. For present illustrative purposes, we take subjunctive conditionals such as ‘If Richard Nixon had pressed the button, there would have been a nuclear war’ to be adequately modelled using the Stalnaker conditional.
Given this semantics for subjunctive conditionals, the motivation for Uniformity becomes very clear. When and , the subjunctives ‘if were true, would be true’ and ‘if were true, would be true’ are both true on the semantics. Now imagine that . This implies that there is some such that the subjunctive ‘If were true, would be true’ is true, but the subjunctive ‘If were true, would be true’ is false. Thus, the following sentence comes out as true:
Clearly, this would be a deeply strange and counterintuitive result. For this reason, we assume that our selection function satisfies the Uniformity condition.7
We are now ready to introduce Lewis’s imaging rule, which will serve as our representative quantitative theory of subjunctive supposition. Stated formally:
Imaging: Given a credence function and any , imaging on results in the credence function defined below.
Intuitively, when is imaged on , each world consistent with keeps all of its original probability, while the prior probability assigned to each world that is inconsistent with is transferred to the closest world satisfying .8
As suggested earlier, conditionalization and imaging differ in whether their recommendations are driven by global or local considerations. Conditionalization recommends the closest credence function that accommodates where the distance between credence functions is interpreted in terms of their global behaviour. In contrast, imaging operates at the local level by shifting credence from each world to the closest world satisfying .
2.2. Lockean Theories of Supposition
With our quantitative accounts of indicative and subjunctive supposition in hand, we will now outline our approach to comparing them with the qualitative theories we will introduce later. As mentioned earlier, qualitative and quantitative theories articulate the norms of suppositional judgement in terms of different kinds of doxastic attitude. Qualitative theories rely on agents’ belief corpora to offer binary judgements about whether they should regard propositions as acceptable under a supposition. Quantitative theories on the other hand use an agent’s credences to generate numerical judgments corresponding to how acceptable agents ought to find each proposition under any given supposition. To directly compare the two we need a way to bridge the gap between qualitative and quantitative attitudes.
To do so, we apply a suitably adapted version of the Lockean Thesis, so-called by Foley (1993). As it is traditionally understood, the Lockean Thesis provides a normative bridge principle between beliefs and credences, which requires that an agent believes that just in case she has “sufficiently high” credence in . This is standardly understood as saying that an agent should believe a proposition if and only if her credence in is at least as great as some Lockean threshold, . Put formally:
Lockean Thesis (LTt): For some : .
This principle will be presupposed as a synchronic coherence requirement used to specify the beliefs that are coherent with an agent’s credences. So, when we are talking about Lockean agents, we will presuppose that they have beliefs and credences satisfying LTt for some . There is an extensive literature on the Lockean Thesis and its motivations.9 Featured prominently in that literature is the Lottery Paradox, first discussed by Kyburg (1961), and the tension it brings to the surface between LTt and the popular normative requirements that beliefs be logically consistent and deductively closed. Primarily for space considerations, we will only briefly engage with that literature at a few points in the next section. Instead, we will unreflectively adopt LTt as a technical tool to aid in our comparative project.
But the Lockean Thesis will play another role in our exploration beyond being a standing synchronic coherence requirement. It will also be used together with the quantitative theories of supposition introduced earlier to construct qualitative suppositional judgments that can be directly compared with the representative qualitative theories of supposition. We begin by introducing the Lockean theory of indicative supposition (LIS) defined below.
LIS: Given a corpus and some , the set of acceptable propositions under the indicative supposition is specified in terms of the operation, , defined below.
Where and are respectively a corpus of beliefs and credence function satisfying LTt and is any proposition, consists of those propositions assigned conditional credence on a value at least . The Lockean theory of subjunctive supposition (LSS) is characterised in an analogous fashion.
LSS: Given a corpus and some , the set of acceptable propositions under the subjunctive supposition is specified in terms of the operation, defined below.
Strictly speaking, the two Lockean operations, and , are not singular operations, but rather each characterise families of operations—one for each . When it is useful, we will restrict our attention to certain subsets of Lockean thresholds by letting and denote the family of operators bounded by the closed interval . Analogous conventions will be adopted for the open and half-open intervals.
3. Indicative Supposition
In their seminal 1985 paper, Alchourrón, Gärdenfors, and Makinson introduced their revision operation ( ). Aside from being the now orthodox account of belief revision, the AGM theory has been understood as an account of indicative supposition. Even Isaac Levi, who was highly critical of AGM as a theory of belief revision, acknowledged that “the AGM approach fares better as an account of suppositional reasoning for the sake of the argument” (1996: 290). We follow suit and present the theory as a normative theory of indicative supposition.
The AGM theory relies on the syntactic representation of epistemic states as “belief sets”, which comprise deductively closed sets of sentences. Formally, this means that is taken to be , where .10 Revising by a sentence delivers the new belief set , understood as the set of sentences that are acceptable under the supposition for an agent with the corpus . This reflects AGM’s presupposition of Cogency as a synchronic coherence requirement on admissible beliefs and suppositional judgments. This requirement, stated below, says that belief corpora and suppositional judgements must be logically consistent and closed under deductive consequence.
Cogency: A set is cogent just in case (i) logically consistent, i.e. , and (ii) is deductively closed, i.e. .
Assuming Cogency results in a coarse-grained representation of epistemic states and suppositional judgments that comes with certain definite costs. For one, since there is just one inconsistent belief set ( ), AGM leaves no room to distinguish between agents with inconsistent beliefs/suppositional judgments. This same belief set represents both an agent who believes, as in the Lottery paradox from Kyburg (1961), each of and also that and another who believes the outright contradiction . Similarly, Nebel (1989) observes that the reasons why beliefs are held are not reflected in this representation. An agent who independently believes that and is represented in the same way as another who believes that on the basis of their beliefs that and . Such dependencies may be important for belief dynamics as seen by considering the possibility that these agents lose their beliefs that . We will not dwell on this point further and simply note that AGM’s Cogency assumption will result in some important divergences between AGM and the Lockean accounts.
The AGM revision operation ( ) is axiomatised by the six “basic Gärdenfors postulates”, 1 – 6, together with the “supplementary postulates”, 7 and 8.
| ( 1) | Closure | |
| ( 2) | Success | |
| ( 3) | Inclusion | |
| ( 4) | If , then | Preservation |
| ( 5) | If , then | Consistency |
| ( 6) | If , then | Extensionality |
| ( 7) | Superexpansion | |
| ( 8) | If , then | Subexpansion |
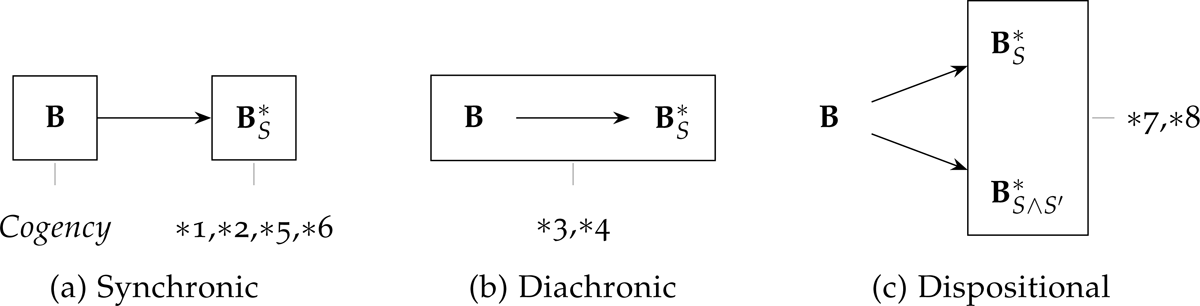
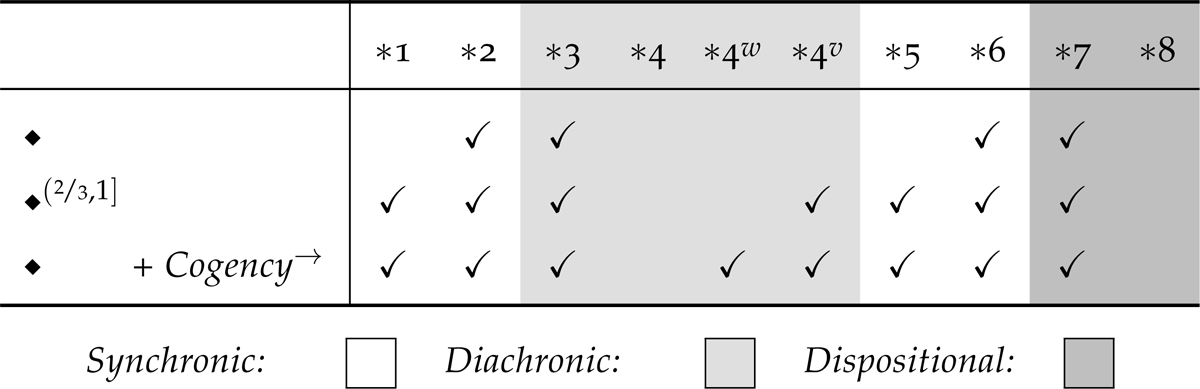
To explain these postulates, it will be instructive to take a brief detour to discuss the types of coherence requirements they encode. Here, we follow Rott (1999a; 2001) in thinking that these postulates include three different types of coherence requirements: synchronic, diachronic, and dispositional. While synchronic coherence provides us with conditions under which a single set of judgments (either a corpus or a set of judgments under a single supposition) hangs together, diachronic coherence accounts for the constraints that the agent’s corpus places on individual sets of suppositional judgments. Lastly, dispositional coherence involves constraints that may be imposed across different sets of suppositional judgments. A visual explanation is provided by the figure below adapted from Rott (1999a: 404).
Whereas Cogency is taken as a background synchronic coherence requirement on belief sets, Closure ( 1) and Consistency ( 5) ensure that suppositional judgments also satisfy Cogency. Since the agent’s beliefs do not play any role in determining the content of these constraints, both postulates are straightforwardly seen as purely synchronic requirements on suppositional judgments. For the same reason, Success ( 2) and Extensionality ( 6) may also be regarded as synchronic requirement on suppositional judgments. Unlike the standing synchronic requirements embodied by 1 and 5, the motivations for 2 and 6 are grounded in constitutive or theoretical considerations about the nature of supposition. We take 2 to be a constitutive requirement of supposition. If supposing that did not result in being accepted, then this would hardly seem like had been supposed at all. On the other hand, 6 captures a theoretical commitment that surface grammar or intensional considerations should play no role in determining which propositions are acceptable under a supposition.11
The next two postulates, Inclusion ( 3) and Preservation12 ( 4), provide AGM’s diachronic coherence requirements. Respectively, these impose upper and lower bounds on the set of suppositional judgments. The restriction imposed by 3 ensures that only propositions that are logically related to or are acceptable under the supposition that . On the other hand, 4 requires that beliefs should not fail to be acceptable under the supposition unless is logically inconsistent with the agent’s corpus. It is worth noting that this places no restrictions on suppositional judgments when the supposition is inconsistent with the agent’s belief set.
Lastly, we have the dispositional coherence requirements given by the two supplementary postulates, Superexpansion ( 7) and Subexpansion ( 8), which respectively generalise 3 and 4. Indeed, in the presence of the eminently plausible Idempotence ( ) principle requiring that , 7 and 8 imply 3 and 4 respectively. Since the supplementary postulates, 7 and 8, encode dispositional coherence requirements, it should be no surprise that the supplementary postulates have been largely discussed in the literature on iterated belief revision.
3.1. LIS and the AGM Postulates
The question now arises: how do the suppositional judgments recommended by LIS relate to those given under the qualitative account based on AGM? A partial answer to this question is given by previously established results. We will complete this picture after surveying the extant results from the literature.
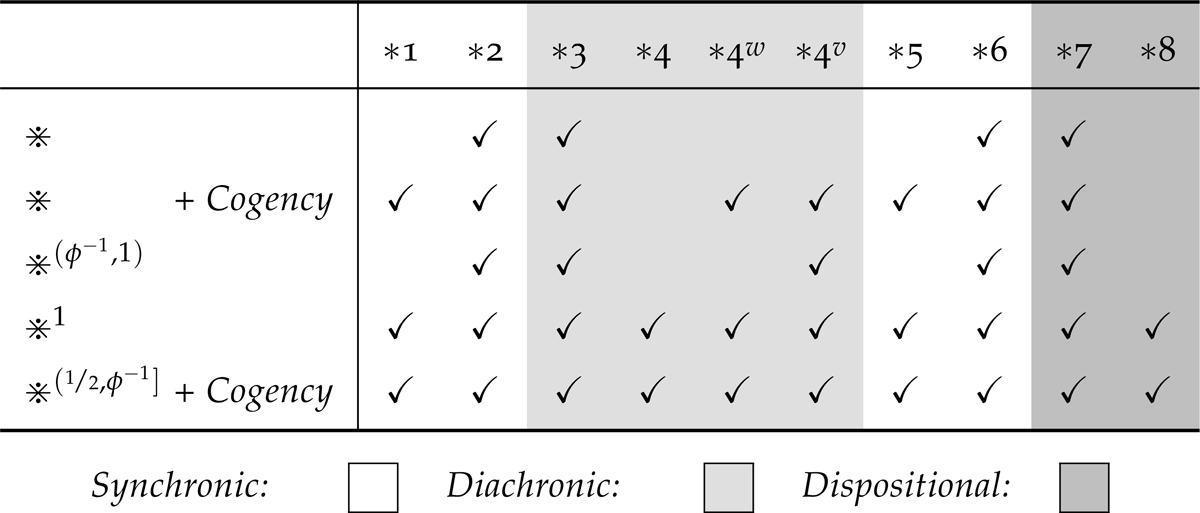
Beginning with their synchronic requirements, there is an immediate tension between LTt and Cogency that has been extensively discussed in the literatures on the Preface and Lottery Paradoxes—these same issues straightforwardly apply to the synchronic requirements imposed by 1 and 5. The remaining basic Gärdenfors postulates have been considered from a Lockean perspective by Shear and Fitelson (2019).13 LIS satisfies both of the remaining AGM synchronic coherence requirements, 2 and 6. Neither result is surprising: LIS satisfies 2 in virtue of the fact that , while the satisfaction of 6 is secured by the extensional character of conditionalization.
The situation is more interesting for the diachronic requirements given by 3 and 4. Interestingly, 3 is satisfied by LIS in full generality. The reason why is relatively easy to see. It is a theorem of the probability calculus that . Thus, whenever it follows that , and so . Turning to the final basic postulate, 4, we see that in general LIS can violate this requirement. The basic reason why is relatively clear, though there are some subtleties that we will discuss. As the characteristic postulate of AGM, 4 says that an agent’s beliefs should remain acceptable under any supposition that is logically consistent with her corpus. However, when an agent is not fully certain of one of her beliefs (say ), it is possible for that some supposition ( ) might be logically consistent with her corpus but still count as counter-evidence to in the sense that . This allows for the possibility that even though and, thus, that but . Still, there are some further constraints that can be imposed under which LIS can be made to satisfy 4.
The explanation immediately above is suggestive of the first situation in which LIS will be guaranteed to satisfy 4. Indeed, Gärdenfors (1988) established a result, which implies that when belief is taken to imply certainty (i.e. when t = 1), LIS will satisfy 4. Moreover, Gärdenfors’s result actually implies that LIS will satisfy all of the AGM postulates. One might wonder then: is the resulting satisfaction of 4 a consequence of the fact that 1 and 5 are satisfied when t = 1?
Shear and Fitelson show that the answer to this question is no, LIS can violate 4 even under the further assumption of Cogency. However, they establish the more surprising result that, assuming Cogency, LIS can only violate 4 when the Lockean threshold is relatively high. In particular, such violations are only possible when the Lockean threshold is at least the inverse of the Golden ratio (i.e. when , where ). As an immediate corollary, assuming both Cogency and that , LIS satisfies all of the basic Gärdenfors postulates, 1 – 6.
But this only tells part of the story about the import of the “Golden threshold” at .14 This is because LIS exhibits interesting behaviour relative to the two weakened variants of Preservation provided below.
| ( 4v) | If , then | Very Weak Preservation |
| ( 4w) | If , then | Weak Preservation |
The first of these postulates, Very Weak Preservation ( 4v), requires that taking something that you already believe as a supposition for the sake of argument should not lead you to reject any of your other beliefs under that supposition. The second, Weak Preservation ( 4w), says that under the same conditions, you should accept anything that you believe.
Although imposing the assumption of Cogency on LIS was not sufficient to guarantee the satisfaction of full Preservation ( 4), it turns out that it is sufficient to ensure that LIS will satisfy both of the weaker requirements, 4v and 4w. However, there is another way to guarantee that LIS will satisfy Very Weak Preservation: if the Lockean threshold is at least , then LIS will satisfy 4v (even without the help of Cogency). These results are summarised in table 2 below.
LIS and Some Variants of Preservation.
| 4 | 4w | 4v | ||
| + Cogency | ||||
| + Cogency | ||||
The import of these results will depend on how you regard 4v, 4w, 4, and Cogency. We regard 4v as eminently reasonable: it would seem very strange to believe both and , but reject under the supposition that . After all, that would mean that ’s certain truth would provide sufficient evidence to accept —that would seem to be ruled out by your concurrent beliefs that and that . For the die-hard Lockeans who reject Cogency, this gives reason to maintain that the Lockean threshold must be a sufficiently high ( ) so as to rule out this possibility. The import of the remaining results is up for debate. A Lockean who finds 4w plausible will be forced into adopting Cogency. However, this would be harder to motivate for a Lockean since once we accept that rational belief need not require certainty, there is no obvious argument in favour of 4w. Still, proponents of AGM who find LIS attractive may take solace in the realisation that their preferred account can be reconciled with LIS through the acceptance of a sufficiently low threshold.15
Thus far, we have presented a number of results concerning LIS and the basic Gärdenfors postulates, 1 – 6, but have not addressed two remaining supplementary postulates, 7 and 8. Shear and Fitelson only mention these postulates in passing, since their primary concern was with the diachronic requirements governing single-step belief change rather than the dispositional requirements that provide bridges between different potential revisions. However, in the context of supposition, dispositional requirements are more obviously relevant. Accordingly, we will now complete the picture by reporting some new results establishing that the relationship between LIS and 3 and 4 carries over to their generalisations given by 7 and 8.
Proposition 1. LIS must satisfy 7. That is, the following is satisfied for any , , and :
Proof. Let , i.e. . Then, letting , we get:
Thus, and so . From this we conclude .
Proposition 2. In the absence of Cogency, LIS can violate 8 for any . That is, if , it is possible that:
Proof. Let be any credence function satisfying the conditions below, where is arbitrarily small:
It is simple to see that case provides the basis for a counterexample to 8 for any threshold in the absence of Cogency.
Proposition 3. The twin requirements of Cogency and are necessary and sufficient to guarantee that LIS satisfies 8.
Proof. Supposing Cogency, we let be consistent with and , and define as a vector on the assignments below.
We start by showing only if , and hence that 8 is satisfied. For contradiction, suppose that , but . Since implies , our assumptions imply
(1)
(2)
First, note that since , by Cogency would imply that . This is equivalent to thus contradicting our assumption that is consistent with . So, (i.e. ) which gives us
(3)
Next, observe that would imply by Cogency that , since . But then , which contradicts 1. So , which implies that
(4)
Taken together, 3 and 4 give us 5, which combined with 3 lets us infer 6.
(5)
(6)
Now, since , we can use the special fact about the Golden Ratio that iff to infer , which contradicts our assumption 1. Thus, our initial assumptions were inconsistent and we infer that assuming together with Cogency suffices to guarantee that LIS satisfies 8.
To see that LIS can violate 8 for any —even under the assumption of Cogency—consider any credence function satisfying the following constraints, where is arbitrarily small:
By construction, we have that and , which shows that but , as desired. Note also that since , . Furthermore, it can be verified that holds for every (and only) , which establishes Cogency and confirms that is consistent with .
This completes our assessment of the relationship between the theories of suppositions provided by LIS and AGM. A full summary of the results from this section is given in table 3 below. In the next section, we turn our attention to the relationship between the subjunctive theories.
4. Subjunctive Supposition
To begin, it will be worthwhile to see why AGM revision would be inappropriate to use as a theory of subjunctive supposition. Consider the following version of the widely discussed adaptation from Peppas (2008) of a classic case from Ginsberg (1986):
Philippa is looking through an open door into a room containing a table, a magazine and a book. One of the two items is on the table and the other is on the floor, but because of poor lighting, Philippa cannot distinguish which is which.
Now, imagine that Philippa thinks to herself, “Suppose that the book were on the floor.” Under this (subjunctive) supposition, what should she accept regarding the location of the magazine? Well, if some ‘local miracle’ occurred that resulted in the book being on the floor, this would not result in a change regarding the location of the magazine. Thus, her judgment regarding the magazine’s location in the suppositional context should remain unchanged from in the categorical one and she should accept that it is either on the table or the floor without accepting either individual disjunct. But, this is not what AGM would recommend. Let and respectively be the propositions ‘the book is on the floor’ and ‘the magazine is on the floor’. For simplicity, let Philippa’s beliefs include only to capture her belief that only that one of the two is on the table. Then, since , we get and so AGM revision would recommend that she accept that the magazine is not on the floor. This is clearly the wrong result.
Cases like these motivated computer science and artificial intelligence researchers to develop alternative belief change operations, known as updates.16 Katsuno and Mendelzon (1992) introduced postulates axiomatising their update operation in similar fashion to the AGM postulates for revision.17 These postulates are formulated below, where saying that is complete means that is a singleton (or equivalently that either or for any sentence ).
| ( 0) | Closure | |
| ( 1) | Success | |
| ( 2) | If then | Stability |
| ( 3) | If and , then | Consistency Preservation |
| ( 4) | If , then | Extensionality |
| ( 5) | Chernoff | |
| ( 6) | If and , then | Reciprocity |
| ( 7) | If is complete, then | Primeness |
| ( 8) | If , then | Compositionality |
Some of these postulates are familiar from the AGM postulates, while some are new. Closure ( 0), Success ( 1), Extensionality ( 4), and Chernoff18 ( 5) are respectively identical to 1, 2, 6, and 7 from earlier. Stability ( 2) and Consistency Preservation ( 3) are each weakened versions of requirements familiar from AGM. Stability ( 2) says that whenever an agent takes one of their beliefs as a supposition, the set of suppositionally acceptable propositions should just be comprised of their beliefs. This is equivalent to 4w together with a version of 3 weakened to only apply when . Just as we think that 3 is unimpeachable, so too is its weakened version. On the other hand, 4w is not on such firm footing. We already saw that this can fail for LIS.19 Consistency Preservation ( 3) offers a weaker consistency requirement than is imposed by 5 and only applies when both the corpus and the supposition are each individually consistent.
The next two postulates are new. Reciprocity ( 6) corresponds to the widely discussed (CSO) axiom of conditional logics. This requirement says that if is acceptable under the supposition that and vice versa, then and generate the same suppositional judgments. Herzig (1998: 127–28) shows that, given 1, 5, and , 6 implies 2. Since these three postulates are relatively innocuous, any reservations about 2 carry over to 6. Primeness ( 7) can be seen as the requirement that when an opinionated agent supposes a disjunction, then their suppositional judgements should satisfy one of its disjuncts. This principle seems appropriate when using a finite language (as in the present case) when we are guaranteed a witness for the truth of a disjunction. It may be less desirable when the language is infinite and there is no such guarantee.
This brings us to KM update’s characteristic postulate, Compositionality20 ( 8), which provides the basis for regarding update as an operation of ‘local belief change’. This is made perspicuous by considering the limiting case in which and where we see that 8 implies that
Thus, when an agent supposes that , she should thereby accept each sentence that would be common to the suppositional judgements recommended for each of the opinionated (viz. complete) belief sets that are consistent with her beliefs. Just as we saw with imaging, the overall set of suppositional judgments is defined as a function of the suppositional judgments thFat would be given at each world consistent with the agent’s opinions. This point has been made in slightly different terms by Pearl (2000: 242). He observes a parallel between 8 and the fact—established by Gärdenfors (1988: 113)—that imaging “preserves mixtures”. That is, if a probability function is a mixture of and , then is a mixture of and . Put more carefully, Gärdenfors’s result shows us that every imaging operator satisfies the condition that if , then . The structural similarity between this condition and 8 helps further reinforce the connection between update and imaging.
Lastly, observe that, as we saw with AGM, the KM postulates encode synchronic, diachronic, and dispositional coherence requirements. The synchronic requirements are given by 0 and 1, the diachronic ones by 2 and 3, and the dispositional requirements are found in the remaining postulates 4 – 8.
4.1. LSS and the KM Postuates
We now proceed to consider how LSS relates to the KM postulates from above. Beginning with the general case where no further constraints are imposed on LSS, we establish which of the KM postulates are satisfied by LSS. As recorded in the proposition below, LSS is guaranteed to satisfy five of the KM postulates: Success ( 1), Consistency Preservation ( 3), Extensionality ( 4), Chernoff ( 5), and Primeness ( 7).
Proposition 4. LSS must satisfy 1, 3, 4, 5 and 7. That is, each of the following is satisfied for any , and :
If and , then
If , then
If is complete, then
Proof. Proceeding sequentially:
Simply recall that to infer and, thus, conclude that LIS must satisfy 1.
First, suppose that and . Next, note that whenever is consistent, if , then . We prove the contrapositive by first supposing that is inconsistent, i.e. . That implies that for any , and hence . But, since is consistent, there is no such that for every , and therefore is also inconsistent.
Suppose that . This implies that just in case . By Uniformity we get and conclude . So, LSS must satisfy 4.
-
To show that LSS must satisfy 5, first suppose so that . Now, we show that if , then . To do so, we assume that . Then, either or . In the first case, we may infer , and by our assumption that , we conclude . In the second case, and so . So either way as desired. Applying the definition of imaging gives us
which imply . From this we may then infer and thus conclude that .
We begin by supposing that is complete, which means that there is a unique world satisfying all propositions in —call this . This implies that . Now, let and infer . Since and , it must be that . Clearly either must satisfy either or . Assuming the former, we infer and thus and so . The same reasoning suffices for the latter. Thus, we infer to conclude that LSS must satisfy 7.
Most of these results will not be unexpected. Success ( 1) should be validated by any plausible account of supposition, while Extensionality ( 4) will hold in any non-hyperintensional account like LSS. The generalisation of ( 3) given by Chernoff ( 5) holds in virtue of the fact that the probability of a material conditional cannot be less than the probability of its consequent. The satisfaction of Primeness ( 7) is intuitive, since if is complete it should already decide either or and updating by their disjunction should not result in more propositions being accepted than by either disjunct. The only result that is remotely surprising is that LSS satisfies Consistency Preservation ( 3). Lockean accounts typically struggle to satisfy consistency requirements. So, it is interesting to note that LSS will not lead you to an inconsistent set of suppositional judgments when your beliefs are consistent.
We turn now to the remaining KM postulates: Closure ( 0), Stability ( 2), Reciprocity ( 6) and Compositionality ( 8). When no additional restrictions are imposed, LSS can violate each as shown below.
Proposition 5. LSS can violate 0, 2, 6, and 8. That is, each of the following is possible:
, but
and ,
, but
Proof. Proceeding sequentially:
To see that LSS can violate 0, simply recall that Lockean accounts generally permit violations of deductive closure, as demonstrated in the Lottery Paradox.
-
A counterexample showing that LSS can violate 2 for any is generated by the assignments provided on the table below, where is arbitrarily small.
It is easy to see that , but .
-
Our counterexample showing that LSS can violate 6 proceeds by assuming that contains the following six possible worlds.
Now, let be such that and select any such that
This gives us and , which implies that and , but and . Note that the choice of played no role here and this suffices as a counterexample to the postulate for any .
-
To build a counterexample showing that LSS can violate 8, fix some threshold , let be arbitrarily small, and let be such that . Then where , let for and . The credence functions , and are defined piecewise below.
Let , , be the Lockean belief sets corresponding to , respectively. It is easy to see that . Imaging each of these credence functions on results in the following assignments.
Thus, we see that .
The first three of these results are expected. As Lockean accounts generally fail to require Cogency, we find that LSS similarly may violate 0. We also see that LSS can violate 2. This postulate is equivalent to the conjunction of 3 and 4. Recall that LIS violated the latter and we find similar behaviour with LSS. Next, the fact that LSS can violate 6 is somewhat obvious. The violation of 8 is somewhat more surprising. As we briefly discussed earlier, 8 is deeply connected to the idea that update proffers a form of ‘local belief change’; and, as we have mentioned, Lewis presents imaging as a method for updating credences by a local dynamics. But, as we will see in the next section, all is not lost.
4.2. Closure under the Stalnaker Conditional Yields Convergence of LSS and KM
When we considered the relationship between the indicative theories given by LIS and AGM, we also saw divergences in the general case—most notably, LIS could violate AGM’s characteristic postulate 4. However, we also saw that the two could be made to converge so long as we assume Cogency and a sufficiently low Lockean threshold. We might then wonder whether there is a similar path towards convergence between LSS and KM.
As we will soon see, there is such a path. However, the requirements involved in establishing convergence between LSS and KM are different. In this case, neither restrictions on the Lockean threshold nor standard Cogency will suffice. Instead, we will augment Cogency with the additional requirement that is closed under the Stalnaker conditional ( ). But this will take some work since our language does not officially include . To deal with this, we will augment our finite propositional language to the “flat fragment” of extended with the Stalnaker conditional. That is, we introduce into the language’s signature to generate , which only adds conditional sentences of the form , where . The statement of Cogency remains unchanged from earlier. However, the type of logical consequence used in the expression of its requirements (Cn) is richer. We let ‘ ’ refer to the stronger requirement that results from imposing Cogency with the richer language . At this stage, there are two important observations to make. Firstly, it is well known that the probability of the Stalnaker conditional is given by the probability of after imaging on , . Thus, the conditions under which Stalnaker conditionals are believed are clear: iff . Second, observe that the Stalnaker conditional satisfies modus ponens, i.e. . This means that requires that and imply .
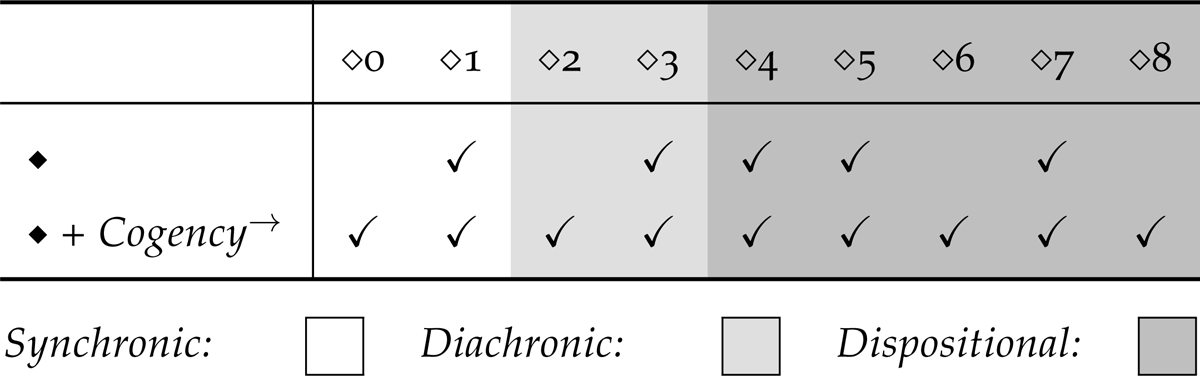
Surprisingly, we find that in this richer environment where we have , LSS satisfies all of the KM postulates. We have already shown that LSS will always satisfy 1, 4, 5, and 7; it is straightforward to see that Propositions 4 and 5 will carry over to this richer environment. So, it remains only to show that, given , the remaining postulates are all satisfied.
Proposition 6. Assuming , LSS must satisfy 0, 2, 6, and 8. That is, for any and , if satisfies , then:
If then
If , and , then
If , then
Proof. As before, we proceed sequentially, where is taken as a standing assumption:
It is an immediate consequence of that LSS satisfies 0.
Suppose that to show that . Let and by infer . This implies . Since imaging on won’t lower the probability of any worlds, it follows that and thus . For the other direction, let so that and hence . By , we get as desired and thus conclude that LSS now satisfies 2.
Suppose that and . This gives us and , from which we infer that and and hence . Now, letting , we infer . By Uniformity and , and jointly entail . Thus we infer and hence . The same argument shows the converse. Thus, given , LSS will satisfy 6.
-
To show that LSS will now satisfy 8, let , and suppose that , and are all , and satisfy LTt with respect to the credence functions , and . Let , . This implies that , , and hence that , , i.e. , . Since is cogent, we have
This implies that , which is a contradiction. So implies , i.e. . Conversely, let , . For argument’s sake, let . This implies that , . and hence that , , i.e. , . Since is cogent, we have
This implies that , which is a contradiction. So implies , i.e. .
The results established in this section are summarised below in table 4, where we see that once is imposed LSS satisfies all of the KM postulates. Perhaps the most important observation is that, in the presence of , the quantitative norms of subjunctive supposition specified by LSS coheres perfectly with the qualitative norms provided by KM. This is in stark contrast to the vexed relationship between LIS and AGM, which falls short of perfect coherence, even when all relevant cogency constraints are imposed.
5. LIS vs. KM and LSS vs. AGM
We have now compared the most prominent extant quantitative theories of indicative and subjunctive supposition to their qualitative counterparts, and identified conditions under which the respective qualitative and qualitative accounts cohere with one another. In this section, we turn to the two further comparisons between (i) the judgments given by LIS that are based on our quantitative indicative theory, and the qualitative subjunctive theory based on KM update, and (ii) those given by LSS that are based on our quantitative subjunctive theory and the qualitative subjunctive theory based on AGM revision.
Our strategy will be the same as before: for (i) we determine which of the KM postulates are satisfied by LIS, and for (ii) we determine which of the AGM postulates are satisfied by LSS. Of course, these comparisons are less conceptually salient than those in Sections 3 and 4. There is no reason to expect quantitative norms of subjunctive (indicative) supposition to cohere with qualitative norms of indicative (subjunctive) supposition. Nonetheless, there are still a couple of reasons why they are worth exploring. One is simply the obvious technical interest in completeness. But, there is a more persuasive reason to consider these comparisons. As we will see, the results of these comparisons will offer a certain dialectical benefit of reinforcing our understanding of the relative importance of certain postulates to indicative and subjunctive supposition.
5.1. LIS vs. KM
We begin by cataloguing the relationship between LIS and KM. In the next two propositions, we consider the general case and establish which of the KM postulates are universally satisfied by LIS and which can be violated. In proposition 7, we see that LIS must satisfy Success ( 1), Extensionality ( 4), and Chernoff ( 5).
Proposition 7. LIS must satisfy 1, 4 and 5. That is, each of the following is satisfied for any , , , and :
If , then
Proof. Since these principles are identical to 2, 6, and 7, respectively, and (as we saw in Section 3) LIS satisfies each of these postulates, LIS must then also satisfy 1, 4, and 5.
Turning now to the postulates, Closure ( 0), Stability ( 2), Consistency Preservation ( 3), Reciprocity ( 6), Primeness ( 7), and Compositionality ( 8), the following proposition establishes that each can be violated by LIS.
Proposition 8. LIS can violate 0, 2, 3, 6, 7 and 8. That is, each of the following is possible:
, but
and , but
and , but
is complete, but
, but
Proof. Proceeding sequentially:
This is immediate since 0 is identical to 1, which LIS can violate.
Simply observe that 2 implies 4w, which can be violated by LIS.
To show that LIS can violate 3, consider the following counterexample. For arbitrary , let be such that , let , and let be arbitrarily small. Finally, let be given by and for . Then , which is consistent. However, is inconsistent since for any .
To see that LIS can violate 6, first recall that LIS can violate 4w (so, it is possible that , but that there is some such that ) and that LIS must satisfy (i.e. ). Now, to find a counterexample to 6, simply find a counterexample to 4w and consider the two revisions: and . By , we know that . And, it is trivial that . But, we also know that and, thus, .
-
For our counterexample to 7, set and let be defined as in the table below.
It is straightforward to see that , , and all satisfy Cogency and constitute a violation of 7: first, note that and so is complete, then observe that , but
-
For our counterexample to 8, fix a threshold and let , , and be defined as in the table below, where arbitrarily small.
Since , we see that all three are complete (thus satisfying Cogency) and that . Now, let and inspect the table below.
Here we find that , , and and thus .
Unsurprisingly, these results show that in general LIS may significantly diverge from the KM postulates. However, we might wonder whether additional constraints can be imposed to bring them closer together. Although we will see that they can become much closer in their behaviour, there is no obvious way to get LIS to satisfy all of the KM postulates. In the postulate below, we show that assuming Cogency recovers 0, 2, 3, and 6. Nonetheless, as foreshadowed in the proofs above for 7 and 8, Cogency is not sufficient to ensure that they are satisfied by LIS.
Proposition 9. Assuming Cogency, LIS must satisfy 0, 2, 3, and 6. That is, assuming Cogency, all of the following are satisfied for any , , , and :
If , then
If and , then
If and , then
Proof. Taking Cogency as a standing assumption, we proceed sequentially:
This is immediate from the assumption of Cogency.
Here, the satisfaction of 2 follows from its equivalence with the conjunction of 3 and 4w. As we saw earlier, LIS always satisfies 3, while Cogency suffices for LIS to satisfy 4w.
This is immediate from the assumption of Cogency.
Let be cogent and let , and . Since is cogent, it follows that , and hence that . It is easy to see that implies . Therefore, from , it follows that . Now, from Cogency and , it follows that , and hence that . The other direction can be proved in analogous fashion.
Interestingly, the following proposition demonstrates that by further adopting a sufficiently low threshold of , we are able to recover 7 (though it is insufficient to recover 8).
Proposition 10. Assuming Cogency, LIS must satisfy 7 just in case .
Proof. Assume Cogency and that . We begin by observing that 7 holds where is consistent with : If is cogent and complete, then is consistent with iff or . But, since LIS satisfies 4w provided Cogency and , this means that or . Either way, LIS satisfies 7. So, it remains to check the case where is inconsistent with . For this case, let our algebra contain the following worlds:
Assuming the antecedent that is complete (together with our assumption that is inconsistent with ) gives us , which in turn implies
(1)
Now, suppose for reductio that . This implies that . But, that can only be the case when . Thus, we infer
(2)
Using 1 and simplifying, we get . Recalling that iff , we infer . Plugging this value back into 1 gives us . With 1 and 2, this gives us , which simplifies to . But, since iff , this contradicts our assumption that .
At this stage, we would like to direct the reader’s attention to a few salient aspects of the results presented in this section. First, it is noteworthy that the conditions which ensure that LIS satisfies 7 are exactly the conditions which ensure LIS satisfies 4 and 8 (and, thus, all of the AGM postulates). On the face of it, this may seem surprising. However, those familiar with the literature may recall that 7 stands in a special relationship to 7 and 8. Gärdenfors (1988: 57) showed that given the basic postulates, 1 – 6, the conjunction of the two supplementary postulates, 7 and 8, is equivalent to the ‘factoring’ condition stated below.
| ( V) | Either (i) or (ii) or (iii) | Factoring |
It is simple to see that V implies and, thus, as a corollary we see that taken together 1 – 8 imply 7. Since LIS satisfies all of the AGM postulates provided Cogency and , it follows that LIS satisfies 7 under the same conditions.
Secondly, it is worth noting explicitly that 8 is the only KM postulate that LIS can violate for any choice of Lockean threshold even under the Cogency assumption.21 This reinforces the already prevalent impression that 8 is in some sense the most distinctive and characteristic KM postulate when it comes to distinguishing between the kinds of belief change embodied by the KM and AGM postulates, respectively.
Finally, it is also worth making explicit the observation, entailed by the preceding analysis, that while there are certain (highly restrictive) conditions under which LIS perfectly coheres with the qualitative norms given by AGM belief revision, there are no similar conditions which ensure coherence of LIS with the qualitative norms given by the KM theory of belief update.
5.2. LSS vs. AGM
We turn now to the second ‘diagonal’ comparison between the theories featuring in table 1. Specifically, we focus now on identifying points of coherence and divergence between the quantitative norms of subjunctive supposition enshrined in LSS and the qualitative norms of indicative supposition encoded in the AGM postulates. Again, we begin with the most general case. Proposition 11 establishes which of the AGM postulates are universally satisfied by LSS, while Proposition 12 reports the divergences.
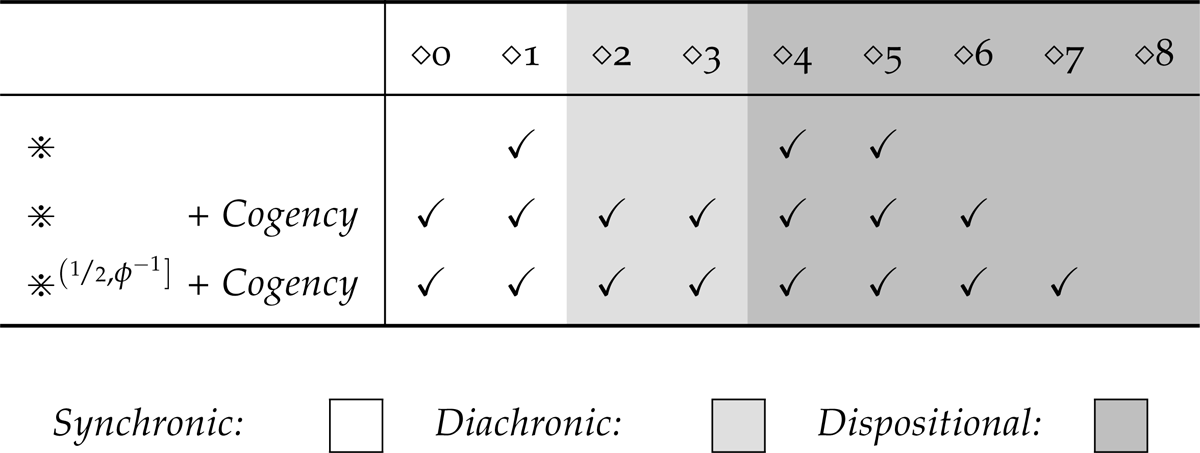
Proposition 11. LSS must satisfy 2, 3, 6, and 7. That is, each of the following is satisfied for any , and :
If , then
Proof. Proceeding sequentially:
In Proposition 4, we saw that LSS satisfies 1, which is identical to 2.
Let . Then , which implies , and thus LSS satisfies 3.
In Proposition 4, we saw that LSS satisfies 4, which is identical to 6.
-
Let . Then , i.e.
Next, note that
Furthermore, for any , iff . This in turn entails by Uniformity that , and hence that . So . So and , as desired.
Proposition 12. LSS can violate 1, 4, 5, and 8. That is, each of the following is possible:
, but
, but
, but
Proof. Proceeding sequentially:
This is immediate from the fact that Lockean agents can violate closure requirements.
-
To show that LSS can violate Preservation for any threshold , even when we assume , let and suppose that and that is as defined below.
This yields the prior belief set and the suppositional judgement set , both satisfying .22 But then we see that , and , since .
This is immediate from the fact that Lockean agents can violate consistency requirements.
-
To see this, let W contain the following worlds.
Now, let be such that so we have . Now, let satisfy the conditions below.
This gives us and , which respectively yield and . All three belief sets, , , and , are cogent. Thus, it’s clear that (i) is consistent with , (ii) and (iii) , which gives us the desired counterexample to 8.
Clearly, the violations of 1 and 5 noted in Proposition 12 are straightforwardly remedied by the assumption of . However, the violation of AGM’s distinctive 4 postulate does not disappear under the assumption, and limiting the range of available Lockean thresholds doesn’t help either. Thus, just as 8 is the one KM postulate that is universally violated by LIS (for all thresholds, and even given the relevant cogency assumption), 4 is the one AGM postulate that is universally violated by LSS (for all thresholds, and even given the relevant cogency assumption). Again, this reinforces the already prevalent impression that just as 8 is the most characteristic norm of subjunctive supposition encoded in the KM postulates, 4 is the most characteristic norm of indicative supposition encoded in the AGM postulates.
Before concluding, we turn briefly to investigating whether, and under what conditions, LSS satisfies the weakenings of 4 discussed in Section 3.
Proposition 13. LSS can violate 4w for any Lockean threshold . That is, for any , it is possible to have even though .
Proof. To see this, consider the following credence function, where is arbitrarily small, and let .
Then and , which gives us but .
Proposition 14. Assuming Cogency, LSS satisfies 4w. That is, entails when we assume Cogency.
Proof. To see this, let . By Cogency, and hence , which entails and hence .
So just as LIS can, in general, violate 4w, but satisfies it in the presence of Cogency, LSS does the same. Turning to its weaker cousin ( 4v) where we saw some interesting behaviour from LIS with respect to the Golden Threshold, we also find some interesting threshold related behaviour. Specifically, the proposition below establishes that just as LIS satisfies 4v when , LSS satisfies 4v when .
Proposition 15. LSS satisfies 4v, for all and only Lockean thresholds . That is, it is possible to have with if and only if .
Proof. Let and assume that . By the assumption, we know that , , which implies . Since imaging by does not decrease the probability of any worlds, we infer and, thus, , which in turn implies . So , as desired. For the other direction, set and let as given below.
Since , the credence function satisfying the conditions and is probabilistic. Since , we have . Now suppose that . Then . So , which is a violation of 4v.
The results established in this section are summarised in table 6 below.
6. Conclusion and Future Work
Recall that one of the basic aims of this paper was to systematically evaluate the claim that ‘imaging is to KM as conditionalization is to AGM’ from the perspective of a Lockean theory of belief and supposition. Below is a summary of the most significant implications of our analysis for this evaluation and an overview of all results from this paper is found in an appendix.
Firstly, there is a significant sense in which our analysis has vindicated the popular analogy between the relationship of conditionalization and AGM on the one hand, and the relationship of imaging and KM, on the other. Specifically, we have shown that while there are conditions—namely, and Cogency—under which LIS coheres perfectly with AGM, there are similarly conditions— —under which LSS coheres perfectly with KM. However, no combination of similar conditions suffice to establish coherence between LIS and KM or between LSS and AGM.
We have also identified the diachronic postulates responsible for the divergences between LIS/LSS and AGM/KM, namely Preservation (and its generalisation Subexpansion)/Compositionality. Apart from these postulates, imposing the synchronic requirements of Cogency/ paves the way for perfect coherence between LIS/LSS and AGM/KM. This offers some formal justification for the intuitive claim that Preservation and Compositionality are the most distinctive diachronic norms of qualitative indicative and subjunctive suppositional reasoning, respectively.
Finally, it is worth emphasising that in the presence of the relevant cogency assumptions, LIS/LSS actually coincide on every AGM/KM postulate other than Compositionality, Preservation, and its generalisation Subexpansion. Thus, the cogency assumptions largely obscure the most central differences between LIS and LSS when it comes to qualitative norms of suppositional judgement. In the absence of cogency assumptions, the differences between LIS and LSS are far greater.
One major problem that arises from our analysis is to find sets of qualitative suppositional reasoning norms that precisely axiomatise LIS and LSS respectively. Such axiomatisations would allow us to pinpoint the qualitative norms that are characteristic of the suppositional reasoning practices of all Lockean agents, and would constitute potentially compelling competitors to the AGM/KM postulates, which have dominated the discussion of qualitative belief change norms ever since their formulation.
Acknowledgements
First and foremost, we would like to single out Hans Rott for his detailed feedback and encouragement, which greatly improved the quality and depth of this paper. We are also appreciative of the valuable feedback received from Francesco Berto, Liam Kofi Bright, Peter Brössel, Catrin Campbell-Moore, Jake Chandler, Jessica Collins, Vincenzo Crupi, James Delgrande, Zoe Drayson, Kenny Easwaran, Eduardo Fermé, Tyrus Fisher, Melissa Fusco, Konstantin Genin, Nina Gierasimczuk, Remco Heesen, Gabriele Kern-Isberner, Hanti Lin, Jason Konek, Tamar Lando Pavlos Peppas, Krzysztof Mierzewski, Julien Murzi, Richard Pettigrew, Patricia Rich, Luis Rosa, Michal Sikorski, Shawn Standefer, and Michael Titelbaum. Lastly, we are grateful to audiences at MIT, the Rutgers Foundations of Probability Seminar, the Formal Epistemology Workshop in Torino, the Australasian Association of Philosophy Conference in Wollongong, the Foundations of Belief Change Workshop at the Pacific Rim International Conference on Artificial Intelligence in Fiji, and the University of Western Australia for their helpful discussions.
Notes
- Note that while individual propositions can be unproblematically identified with their corresponding truth sets, the same is not true for sets of propositions, since there can exist such that . ⮭
- While their 1985 paper, cited above, was the first full characterisation of AGM’s revision operator, this work was the fusion of two independent projects. Alchourrón and Makinson (1981; 1982) had previously been investigating the derogation and revision of legal codes, while Gärdenfors (1978; 1981) had done considerable work on conditionals and belief change. ⮭
- It is worth mentioning that KM is not normally presented as a theory of subjunctive supposition. One of this paper’s main contributions is a novel argument for viewing the KM axioms as qualitative rationality norms for subjunctive supposition. ⮭
- Although this motivation for update as a distinct process from revision is prima facie plausible, it is only satisfactory for limited applications. Friedman and Halpern (1999) have persuasively argued that there are no deep difference between these two types of operations. In particular, they show that the apparent difference between revisions and updates can be recast as a relic of the chosen language. What may be described as a dynamically changing world in one language can be redescribed as a static world using appropriate temporal indices. It may be useful to retain the distinction between revision and update in areas like computer science where there is genuine import to the language in which a database management procedure is implemented. However, in epistemology, where questions are less bound to syntactic matters, other motivation is needed. Still, we see value in the distinction when these operations are understood in terms of supposition rather than belief change. ⮭
- The “epistemic”/“ontic” terminology was introduced in a series of papers by Lindström and Rabinowicz (1992b; 1992a; 1998) discussing indicative and subjunctive conditionals. It is widely acknowledged that the correspondence between indicative/subjunctive conditionals and epistemic/ontic conditionals is not perfect—there are a number of cases where the two come apart; see Rott (1999b). The same is true for supposition. Still, for the purposes of this paper, we will ignore these imperfections and rely on the indicative/subjunctive terminology to capture the epistemic/ontic distinction. ⮭
- Ahmed (2014) provides further explanation of the difference between evidential and causal decision theory from the perspective of an evidentialist, while Joyce (1999) does so from the point of view of a causalist. ⮭
- Note that the Uniformity condition can also be directly motivated in terms of subjunctive supposition (and without reference to subjunctive conditionals), since failures of Uniformity imply that it is sometimes rational to (i) believe upon subjunctively supposing , (ii) believe upon subjunctively supposing , (iii) believe upon subjunctively supposing , (iv) believe upon subjunctively supposing . Although this is less obviously bizarre than the problems that Uniformity violations create for the semantics of subjunctive conditionals, it is also a puzzling and intuitively irrational form of suppositional reasoning. ⮭
- For generalisations of Lewis’s imaging rule that allow for more than one closest world, see Gärdenfors (1982), Joyce (1999). For a generalisation of imaging to the context of partial supposition analogous to Jeffrey’s generalisation of Bayesian conditionalization, see Eva and Hartmann (2021). ⮭
- Further discussion can be found in Easwaran (2016), Leitgeb (2017), Dorst (2019), Douven and Rott (2018), Schurz (2019), and Jackson (2020). ⮭
- For present purposes, we assume that is the classical consequence relation, however, this is strictly speaking more than is required. In the theory’s original formulation, can be any consistent, compact, and supraclassical consequence relation satisfying modus ponens and the deduction theorem. ⮭
- While we embrace this commitment for present purposes, it should be acknowledged that there is room to disagree here. One might think that suppositional judgments should be hyperintensional due to considerations of topic-sensitivity or relevance. A recent discussion of these matters in the context of AGM is available in Berto (2019). ⮭
- The original formulation of these postulates do not include Preservation and, instead, include the stronger Vacuity principle requiring that if , then . However, Preservation implies Vacuity in the context of Closure and Success and is preferable for both aesthetic and conceptual reasons. ⮭
- Their investigations into the contrasting diachronic coherence requirements of Lockeanism and AGM explored a “Lockean revision” operation, which is formally identical to the operation characterising LIS. For an alternative presentation of their results and some discussion, see Genin (2019). ⮭
- For further results illustrating the significance of for conditional reasoning in Lockean agents, see Eva (2020). ⮭
- This is not the only way of reconciling Lockeanism with AGM. Building on his Stability Theory of Belief, Leitgeb (2013; 2017) has recently proposed a belief revision operator satisfying the Lockean thesis and all of the AGM postulates. However, that approach comes with certain definitive costs that have been discussed in the literature; see Titelbaum (2021) for further discussion of these issues. ⮭
- The first account of update was given by Winslett (1988) with her “Possible Models Approach”, which built on earlier work from Ginsberg (1986) and Ginsberg and Smith (1987; 1988). Notable subsequent offerings are given in Winslett (1990), Dalal (1988), Forbus (1989), Zhang and Foo (1996), and Herzig (1996). A systematic comparison of how these operations relate to the KM postulates, introduced below, is provided by Herzig and Rifi (1999). ⮭
- These postulates were originally stated in a more semantic formalism. For continuity with the AGM postulates, we provide them using an equivalent syntactic formulation. ⮭
- Following the terminology used in an unpublished manuscript by Jessica Collins, we adopt this alternative name for the Superexpansion postulate from AGM in honour of Herman Chernoff (1954) who proposed an analogous principle in the context of finite choice functions. ⮭
- Moreover, Herzig and Rifi (1999) show that this postulate is not satisfied by many of the competing update operators to KM update mentioned in footnote 16. ⮭
- While Katsuno and Mendelzon call this the “Disjunction Rule”, we prefer the terminology from Collins (1991), which we feel better captures the intuitive content of the postulate. ⮭
- To verify this, see the counterexample to 8 provided in Proposition 8. ⮭
- Of course, these belief sets will also contain some Stalnaker conditionals, but we can define the selection functions to ensure the satisfaction of . ⮭
References
1 Adams, Ernest W. (1970). Subjunctive and Indicative Conditionals. Foundations of Language, 6(1), 89–94.
2 Ahmed, Arif (2014). Evidence, Decision, and Causality. Cambridge University Press.
3 Alchourrón, Carlos E., Peter Gärdenfors, and David Makinson (1985). On the Logic of Theory Change: Partial Meet Contraction and Revision Functions. The Journal of Symbolic Logic, 50(2), 510–30.
4 Alchourrón, Carlos E. and David Makinson (1981). Hierarchies of Regulation and their Logic. In Risto Hilpinen (Ed.), New Studies in Deontic Logic: Norms, Actions, and the Foundations of Ethics (125–48). D. Reidel.
5 Alchourrón, Carlos E. and David Makinson (1982). On the Logic of Theory Change: Contraction Functions and Their Associated Revision Functions. Theoria, 48(1), 14–37.
6 Bayes, Thomas (1763). An Essay Towards Solving a Problem in the Doctrine of Chances. Transactions of the Royal Society of London, 53, 370–418.
7 Berto, Francesco (2019). Simple Hyperintensional Belief Revision. Erkenntnis, 84(3), 559–75.
8 Chernoff, Herman (1954). Rational Selection of Decision Functions. Econometrica, 22(4), 422–43.
9 Collins, J. (1991). Belief Revision (Doctoral dissertation, Princeton University).
10 Dalal, Mukesh (1988). Investigations into a Theory of Knowledge Base Revision: Preliminary Report. In Howard E. Shrobe, Tom M. Mitchell, and Reid G. Smith (Eds.), AAAI’88: Proceedings of the Seventh AAAI National Conference on Artificial Intelligence (475–79). AAAI Press.
11 Dorst, Kevin (2019). Lockeans Maximize Expected Accuracy. Mind, 128(509), 175–211.
12 Douven, Igor and Hans Rott (2018). From Probabilities to Categorical Beliefs: Going beyond Toy Models. Journal of Logic and Computation, 28(6), 1099–124.
13 Easwaran, Kenny (2016). Dr. Truthlove or: How I Learned to Stop Worrying and Love Bayesian Probabilities. Noûs, 50(4), 816–53.
14 Eva, Benjamin (2020). The Logic of Conditional Belief. Philosophical Quarterly, 70(281), 759–79.
15 Eva, Benjamin and Stephan Hartmann (2021). The Logic of Partial Supposition. Analysis, 81(2), 215–24.
16 Foley, Richard (1993). Working without a Net: A Study of Egocentric Epistemology. Oxford University Press.
17 Forbus, Kenneth D. (1989). Introducing Actions into Qualitative Simulation. In Natesa S. Sridharan (Ed.), Proceedings of the 11th International Joint Conference on Artificial Intelligence (1273–78). Morgan Kaufmann.
18 Friedman, Nir and Joseph Y. Halpern (1999). Modeling Belief in Dynamic Systems, Part II: Revision and Update. Journal of Artificial Intelligence Research, 10(1), 117–67.
19 Gärdenfors, Peter (1978). Conditionals and Changes of Belief. In Ilkka Niiniluoto and Raimo Tuomela (Eds.), The Logic and Epistemology of Scientific Change (381–404). North Holland.
20 Gärdenfors, Peter (1981). An Epistemic Approach to Conditionals. American Philosophical Quarterly, 18(3), 203–11.
21 Gärdenfors, Peter (1982). Imaging and Conditionalization. The Journal of Philosophy, 79(12), 747–60.
22 Gärdenfors, Peter (1988). Knowledge in Flux: Modeling the Dynamics of Epistemic States. MIT Press.
23 Genin, Konstantin (2019). Full & Partial Belief. In Richard Pettigrew and Jonathan Weisberg (Eds.), The Open Handbook of Formal Epistemology (437–98). PhilPapers Foundation.
24 Ginsberg, Matthew L. (1986). Counterfactuals. Artificial Intelligence, 30(1), 35–79.
25 Ginsberg, Matthew L. and David E. Smith (1987). Possible Worlds and the Qualification Problem. In Kenneth D. Forbus and Howard E. Shrobe (Eds.), AAAI’87: Proceedings of the Sixth National Conference on Artificial Intelligence (212–17). Morgan Kaufmann.
26 Ginsberg, Matthew L. and David E. Smith (1988). Reasoning About Action I: A Possible Worlds Approach. Artificial Intelligence, 35(2), 165–95.
27 Herzig, Andreas (1996). The PMA Revisited. In Luigia Carlucci Aiello, Jon Doyle, and Stuart C. Shapiro (Eds.), Proceedings of the Fifth International Conference on Principles of Knowledge Representation and Reasoning (KR’96) (40–50). Morgan Kaufmann.
28 Herzig, Andreas (1998). Logics for Belief Base Updating. In Didier Dubois and Henri Prade (Eds.), Belief Change (189–231). Springer.
29 Herzig, Andreas and Omar Rifi (1999). Propositional Belief Base Update and Minimal Change. Artificial Intelligence, 115(1), 107–38.
30 Jackson, Elizabeth G. (2020). The Relationship between Belief and Credence. Philosophy Compass, 15(6), 1–13.
31 Joyce, James M. (1999). The Foundations of Causal Decision Theory. Cambridge University Press.
32 Katsuno, Hirofumi and Alberto O. Mendelzon (1992). On the Difference between Updating a Knowledge Base and Revising it. In Peter Gärdenfors (Ed.), Belief Revision (183–203). Cambridge University Press.
33 Keller, Arthur M. and Marianne Winslett Wilkins (1985). On the Use of an Extended Relational Model to Handle Changing Incomplete Information. IEEE Transactions on Software Engineering, 11(7), 620–33.
34 Kyburg, Henry E. (1961). Probability and the Logic of Rational Belief. Wesleyan University Press.
35 Leitgeb, Hannes (2013). The Review Paradox: On The Diachronic Costs of Not Closing Rational Belief under Conjunction. Noûs, 78(4), 781–93.
36 Leitgeb, Hannes (2017). The Stability Theory of Belief: How Rational Belief Coheres with Probability. Oxford University Press.
37 Levi, Isaac (1996). For the Sake of Argument. Cambridge University Press.
38 Lewis, David (1976). Probabilities of Conditionals and Conditional Probabilities. The Philosophical Review, 85(3), 297–315.
39 Lindström, Sten and Wlodek Rabinowicz (1992a). Belief Revision, Epistemic Conditionals and the Ramsey Test. Synthese, 91(2), 195–237.
40 Lindström, Sten and Wlodek Rabinowicz (1992b). The Ramsey Test Revisited. Theoria, 58(2–3), 131–82.
41 Lindström, Sten and Wlodek Rabinowicz (1998). Conditionals and the Ramsey Test. In Didier Dubois and Henri Prade (Eds.), Belief Change (147–88). Springer.
42 Nebel, Bernhard (1989). A Knowledge Level Analysis of Belief Revision. In Ronald J. Brachman, Hector J. Levesque, and Raymond Reiter (Eds.), Proceedings of the First International Conference on Principles of Knowledge Representation and Reasoning (KR’89) (301–11). Morgan Kaufmann.
43 Pearl, Judea (2000). Causality: Models, Reasoning, and Inference. Cambridge University Press.
44 Peppas, Pavlos (2008). Belief Revision. In Frank van Harmelen, Vladimir Lifschitz, and Bruce Porter (Eds.), Handbook of Knowledge Representation (317–59). Elsevier.
45 Rott, Hans (1999a). Coherence and Conservatism in the Dynamics of Belief Part I: Finding the Right Framework. Erkenntnis, 50(2/3), 387–412.
46 Rott, Hans (1999b). Moody Conditionals: Hamburgers, Switches, and the Tragic Death of an American President. In Jelle Gerbrandy, Maarten Marx, Maarten de Rijke, and Yde Venema (Eds.), JFAK. Essays Dedicated to Johan van Benthem on the Occasion of His 50th Birthday. Amsterdam University Press.
47 Rott, Hans (2001). Change, Choice and Inference: A Study of Belief Revision and Nonmonotonic Reasoning. Oxford University Press.
48 Russell, Bertrand (1904). Meinong’s Theory of Complexes and Assumptions II. Mind, 13(1), 336–54.
49 Schurz, Gerhard (2019). Impossibility Results for Rational Belief. Noûs, 53(1), 134–59.
50 Shear, Ted and Branden Fitelson (2019). Two Approaches to Belief Revision. Erkenntnis, 84(3), 487–518.
51 Stalnaker, Robert (1968). A Theory of Conditionals. In Nicholas Rescher (Ed.) Studies in Logical Theory (98–112). Blackwell.
52 Titelbaum, Michael G. (2021). The Stability of Belief: How Rational Belief Coheres with Probability, by Hannes Leitgeb. Mind, 130(519), 1006–17.
53 Winslett, Marianne (1988). Reasoning about Action Using a Possible Models Approach. In Howard E. Shrobe, Tom M. Mitchell, and Reid G. Smith (Eds.), AAAI-88: Proceedings of the Seventh National Conference on Artificial Intelligence (89–93). AAAI Press.
54 Winslett, Marianne (1990). Updating Logical Databases. Cambridge University Press.
55 Zhang, Yan and Norman Y. Foo (1996). Updating Knowledge Bases with Disjunctive Information. In William J. Clancey and Daniel S. Weld (Eds.), AAAI-96: Proceedings of the Thirteenth National Conference on Artificial Intelligence (562–68). AAAI Press.