Fallibility without Facts

Will Gamester; Will Gamester

doi:10.3998/ergo.2241

Suppose that the function of normative thought and talk—about what is right or wrong, good or bad, or what may, ought, or must be done—is to represent or describe the world. Then it’s straightforward to see how normative judgements can be correct or incorrect. A normative judgement is correct iff the world is as the judgement represents it as being. According to normative expressivism, however, the function of normative discourse is not to describe the world, but to express desire-like states—states that serve a motivational, rather than representational, role—such as desires, plans, preferences, or attitudes of approval and disapproval.^¹ So how can the expressivist make sense of the idea that there are correct and incorrect normative judgements? Call this the Correctness Challenge.

We can make some progress by appealing to normative (dis)agreement.^² Suppose I think that eating meat is wrong. I thus think that anyone who agrees with me has the correct view on the matter and anyone who disagrees with me has the incorrect view. But this gives me no way of making sense of the possibility that anyone I presently agree with (including me) is in the wrong, nor that anyone I don’t presently agree with is in the right. Call this the Fallibility Challenge.

Simon Blackburn (1993: 127) calls “expressions of moral fallibility […] the hardest context of all for an [expressivist] to understand.” He proposes that I make sense of my fallibility in terms of the possibility that my judgements might be unstable through improvement. While I think that eating meat is wrong, I might change my mind if I were, say, more informed or coherent. Call this the Instability Proposal.

However, this leaves no room for the possibility that my judgement might be stable through all improvements and yet mistaken. Whether or not such a hypothesis is plausible, it seems coherent; so we should be able to make sense of it. Call this the Limited Fallibility Objection. Moreover, Andy Egan (2007) argues that the Instability Proposal engenders an implausible asymmetry between myself and others by my own lights. Roughly: I cannot make sense of the possibility that a judgement of my own is stable and yet mistaken, but I can make sense of the possibility that a judgement of yours is stable and yet mistaken. So, I am immune to a kind of error to which you are vulnerable. Egan, co-opting a turn of phrase from Blackburn, labels this asymmetry “unpardonably smug”. Call this the Smugness Objection.

This debate has generated a small literature, including responses from Blackburn (2009), Lenman (2014), Horgan and Timmons (2015), Ridge (2015), and Bex-Priestley (2018).^³ These responses are inadequate—see §3.2.1. More importantly, however, neither the Instability Proposal nor the Limited Fallibility and Smugness Objections have yet been worked out in sufficient detail for us to be able to adjudicate the dispute. My goal in this paper is to do better.

§1 clarifies the Correctness and Fallibility Challenges, distinguishes three response strategies, and makes the case for pursuing the strategy pursued here. §2 develops a version of the Instability Proposal by constructing a general, non-representational theory of normative (in)correctness that vindicates the expressivist’s conception of the nature of normative inquiry. §3 responds to objections, arguing that my theory leaves sufficient room for my own fallibility and is immune to the charge of “smugness”. Central to the response to the Smugness Objection is the appeal to indeterminacy in cases of fundamental normative disagreement between reasonable normative outlooks.

1. Expressivism, Correctness, and Fallibility

1.1. The Correctness Challenge

Expressivists, unlike representationalist-realists, do not believe in an antecedently given normative ontology, in the following sense. The expressivist argues that we do not get an informative explanation of normative discourse if we start out by postulating a realm of normative properties, relations, or facts that such discourse functions to describe. We therefore cannot appeal to such an ontology to determine which normative judgements are correct.

Error theorists, of course, say something similar. But for the error theorist a normative judgement is a representational state that would be correct if there were anything in the world for it to correspond to. Because there are no such entities, normative discourse is systematically in error. The expressivist argues that this misunderstands the nature of normative judgement. Normative judgements are not, in the first instance, to be construed as representational states, but as motivational, desire-like states. Since such states do not function to represent the world, they cannot be accused of systematically misrepresenting the world.

The worry is that this over-works: it seems to give up the very possibility of failure, and with it the possibility of success. Hence the Correctness Challenge. If normative discourse does not serve a representational function, then success and failure in normative inquiry—correctness and incorrectness, truth and falsity—cannot be understood representationally. But then how are they to be understood?

1.2. Three Responses

There are three possible responses to this challenge:^⁴

Explain normative (in)correctness non-representationally.
Earn the right to explain normative (in)correctness representationally.
Reject it as a pseudo-problem.

A non-representational account of normative correctness explains what it is for a normative judgement to be correct without appealing to a normative ontology. As a silly example, suppose we say that a normative judgement is correct iff I agree with it. This is a non-representational account of correctness, and thus one the expressivist is entitled to. But it is obviously implausible: among other things, it entails that I cannot be mistaken about normative matters. The Fallibility Challenge thus emerges as a constraint on strategy (1): a non-representational explanation of normative (in)correctness needs to leave sufficient room for my own fallibility. (This is intentionally vague: how much room is “sufficient” is a live question with which we’ll engage below.)

In §§2–3, I develop a non-representational theory of normative (in)correctness that, I argue, satisfies this constraint. Those convinced of the interest of this strategy can skip to §2. In the rest of this section, I explain why I prefer strategy (1) to strategies (2) or (3), and why advocates of other strategies should be interested in the discussion below anyway.

1.3. Strategy (2)

The contemporary expressivist may not start by postulating a normative ontology or construing normative judgements as representational states, but nor does she typically deny that there are normative properties, relations, facts, or beliefs. The now-orthodox move is to “earn the right” to this “realist”-sounding talk.^⁵ Perhaps, then, in earning the right to talk of normative facts and beliefs, the expressivist will ipso facto earn the right to a representational explanation of normative (in)correctness. This is strategy (2).

Whether this works turns on how we go about earning the right to realist-representationalist talk. The most prominent approach appeals to deflationism or minimalism about the relevant terminology.^⁶ The blueprint comes from deflationism about truth, which postulates a strong equivalence between ‘It is true that $p$ ’ and ‘ $p$ ’,^⁷ such that ‘It is true that eating meat is wrong’ is, more or less, just another way of saying ‘Eating meat is wrong’. So, in explaining what it means to say that eating meat is wrong (as the expression of a desire-like state), the expressivist ipso facto explains what it means to say that it is true that eating meat is wrong—and so is entitled, via existential generalisation, to say that there are normative truths. Through similar equivalence claims, the expressivist may be entitled to talk of normative properties, facts, and beliefs: if, for example, we say that ‘ $a$ instantiates the property of $F$ ness’, ‘It is a fact that $a$ is $F$ ’, and ‘It is correct to believe that $a$ is $F$ ’, are all equivalent to ‘ $a$ is $F$ ’.

Now, if I think that eating meat is wrong, then deflationism entitles me to say that it is a fact that eating meat is wrong. But this gives me no way of making sense of the possibility that it is not a fact that eating meat is wrong, or that it is a fact that eating meat is not wrong, or generally that the normative facts are other than I take them to be. So, this way of earning the right to talk of normative facts gives me no way to make sense of my own fallibility—it is no better off that the crude non-representational account from §1.2. This is disappointing, but unsurprising. The core claim of deflationism is precisely that talk of “truth”, “facts”, etc. is not suited to do substantive explanatory work, but merely allows me to re-state my first-order normative judgements in novel terms; that is, to say what I could already say in a new way. So, unless I can already make sense of my normative fallibility, deflationism is by its nature impotent to help.^⁸

However, it’s hard to see how else to pursue strategy (2): a more substantive, non-representational account of, say, normative truth or correctness would be an instance of strategy (1).

1.4. Strategy (3)

There may, however, be a role for deflationism in strategy (3). If, for instance, ‘it is correct to believe that $p$ ’ just means what ‘ $p$ ’ means, then the following questions become equivalent:

(A1) What makes it the case that it is (in)correct to believe that eating meat is wrong?
(A2) What makes it the case that eating meat is (not) wrong?

And (A2) is arguably not a metanormative question at all, but a first-order normative question; and so not something the expressivist qua expressivist owes us an answer to. So, the expressivist might deny that she can make sense of the Correctness Challenge as distinct from a first-order normative issue. That’s strategy (3).

This is in keeping with the expressivist’s “sideways-on” methodology: the expressivist explains what it is to think that φ-ing is wrong; but she denies that there is any interesting “metaphysical” question about what it is for φ-ing to be wrong besides the first-order question: is φ-ing wrong? Likewise, the expressivist might say that to think that a judgement is (in)correct is just to (dis)agree with it; but there is no interesting “metaphysical” question about what it is for a judgement to be (in)correct besides the first-order question: is the judgement (in)correct?^⁹

There is more to say about this than I can say here, but it is hard to find this rejection of the challenge satisfying. The initial puzzlement arises because the expressivist maintains that normative judgements—presumably unlike other judgements—are desire-like states, which play a motivational role, rather than a representational role. Since such judgements cannot be (in)correct in virtue of (in)accurately representing an antecedently given normative ontology, it’s puzzling how they can be (in)correct at all. Strategy (3) tries to sidestep the worry by saying that the question of what makes it the case that a certain judgement is correct, like (A1), is in fact equivalent to a first-order question, like (A2), which is to be answered by engaging in first-order normative inquiry. Now, that might be of comfort if we were already satisfied that first-order normative inquiry is the type of thing that can issue in correct and incorrect judgements. But that is precisely what we were puzzled about. So it is strange to conclude that this somehow shows that our initial puzzlement was ill-founded. On the contrary, what follows from the claim that (A1) is equivalent to (A2) is that any answer to the question will express a desire-like state, rather than a representational state. But that is just another instance of the claim that gave rise to the initial puzzlement! Rather than dissolving the worry, then, strategy (3) just seems to bring us around in a tight circle. I for one feel none-the-wiser for it—just a bit dizzier.

However, even those committed to strategy (3) should be interested in my development of strategy (1), for at least four reasons. First, strategy (3) seems to rely on deflationism, which is independently contentious. It’d be better if the expressivist didn’t have to give away this hostage to fortune. Second, strategy (3) also runs into a version of the Fallibility Challenge. It is incoherent for me to think de re of any judgement I agree with that it is mistaken, or of any judgement that I don’t agree with that it is correct. But it’s coherent to think that a judgement I agree with might be mistaken.^¹⁰ So we can ask: what it is to think that I might be mistaken? One can understand the Instability Proposal, as Blackburn (2009) does, as an answer to this sideways-on question, rather than an instance of strategy (1).^¹¹

Third, as will become clear, it’s difficult to see how the expressivist can avoid commitment to the substantive theory of normative (in)correctness developed below, given how she conceives of normative inquiry. Finally, even if some expressivists are happy to avoid meeting the Correctness Challenge head-on, critics and undecided neutrals may well count this as a mark against them. It is therefore dialectically advantageous if we can show that the expressivist can meet the challenge head-on, even if this is not her own preferred strategy.

2. Normative Correctness for Expressivists

So, our goal is to answer the Correctness Challenge by constructing a non-representational theory of normative (in)correctness that leaves sufficient room for my own normative fallibility. The primary inspiration for the account will be Blackburn’s Instability Proposal. The following passage, ubiquitous in the relevant literature,^¹² summarises the central idea:

How can I make sense of fears of my own fallibility? Well, there are a number of things I admire: for instance, information, sensitivity, maturity, imagination, coherence. I know that other people show defects in these respects, and that these defects lead to bad opinions. But can I exempt myself from the same possibility? Of course not (that would be unpardonably smug). So I can think that perhaps some of my opinions are due to defects of information, sensitivity, maturity, imagination, and coherence. If I really set out to investigate whether this is true, I stand on one part of the (Neurath) boat and inspect the other parts. (Blackburn 1998: 318)

My strategy is as follows. I extract from Blackburn a conception of the nature of normative inquiry (§2.1). Building on this, I explore, in the abstract, what could happen to a particular normative judgement as one successfully engages in normative inquiry (§2.2). I then consider the theoretical significance of this abstract exploration (§2.3). This enables us to see our way clear to a theory of normative (in)correctness that vindicates normative inquiry as the expressivist conceives of it (§2.4).

2.1. Normative Inquiry for Expressivists

In addition to first-order normative judgements, agents make higher-order normative judgements. Higher-order norms are “norms [that] govern the acceptance of other norms” (Gibbard 1990: 198).^¹³ For the expressivist, the formation and maintenance of your normative outlook is guided by your acceptance of higher-order norms. For instance, Blackburn thinks that a normative outlook that is more informed, sensitive, imaginative, mature, and/or coherent than another is to that extent better; that we ought to have normative outlooks that are more informed, sensitive, imaginative, mature, coherent. In engaging in normative inquiry, then, Blackburn will seek to become more informed, sensitive, imaginative, mature, and coherent.

Using higher-order normative judgements, we can make sense of the idea that one normative outlook $x$ is better than another $y$ by the lights of a third $z$ ; where this is so iff it follows from $z$ ’s higher-order normative judgements and the non-normative facts that $x$ is better than $y$ . For instance, if your opinions on animal ethics are, in fact, more informed, sensitive, imaginative, mature, and coherent than mine,^¹⁴ then your normative outlook is better than mine by Blackburn’s lights. We’ll symbolise this thus:

x > z y .

In engaging in normative inquiry, I’m trying to make my normative outlook better by my own lights. I successfully engage in normative inquiry if I succeed in doing so.

Higher-order normative judgements are themselves normative judgements, so my acceptance of a higher-order norm will itself be governed by higher-order norms.^¹⁵ This raises a question about the structure of our higher-order normative judgements. They could be hierarchically structured: first-order judgements are governed by second-order judgements; second-order by third-order; and so on.^¹⁶ To avoid an infinite regress, we’d need highest-order normative judgements, whose acceptance is not governed by other norms. I find this unattractive.^¹⁷ On my preferred view, we instead embrace a “Neurath’s Boat”-style epistemology: one’s acceptance of any particular higher-order norm is itself governed by one’s acceptance of other higher-order norms.^¹⁸

So, my higher-order normative judgements may change as I successfully engage in normative inquiry. Nonetheless, at any stage I will be trying to make my normative outlook better by the lights of the higher-order normative judgements that I endorse at that time.

We can capture this idea by recursively defining a notion of accessibility: a normative outlook $x$ is accessible from another $y ($ ‘ $x > y$ ’) iff either $x$ is better than $y$ by $y$ ’s lights, or there is some normative outlook $z$ , such that $x$ is accessible from $z$ , and $z$ is better than $y$ by $y$ ’s lights.

Accessibility

$x > y ≝ x > y y ∨ ∃ z (x > z & z > y y)$ .

Intuitively, $x$ is accessible from $y$ if we can get from $y$ to $x$ via a series of incremental changes, each of which is an improvement by the lights of the outlook being changed. Call this process self-improvement. The recursivity of the definition guarantees that accessibility is transitive.

This allows us to define, for any normative outlook $x$ , its improvement* set, $X$ , which is the set of normative outlooks accessible from $x$ , plus $x$ itself. (Including $x$ is just a formal choice.) Intuitively, your improvement* set consists of every possible normative outlook you could end up with by going through the process of self-improvement; that is, by successfully engaging in normative inquiry, as the expressivist conceives of it.^¹⁹

2.2. Outcomes of Self-Improvement

Given the above, we can reflect on what may happen to any particular judgement as one successfully engages in normative inquiry. It will be useful in what follows to have some light formalism to express ideas precisely. To that end, we’ll put square-brackets around a sentence to represent the judgement expressed by that sentence: “ $[p]$ ” represents the judgement that $p$ . Continuing to use lower-case letters “ $x$ ”, “ $y$ ”, and “ $z$ ” as variables ranging over normative outlooks, “ $[p] ∈ x$ ” means $x$ thinks that $p$ , and “ $[p]$ ∉ $x$ ” means $x$ does not think that $p$ . Given that one can suspend judgement, not thinking that $p$ does not entail thinking that not- $p$ ; so “ $[p] ∉ x$ ” should not be confused with “ $[¬ p] ∈ x$ ”. For the same reason, we’ll use “not- $[p]$ ” to represent the absence of the judgement that $p$ ; where “ $[¬ p]$ ” represents the judgement that $¬ p$ .

2.2.1. Stable-Points and Unstable-Points

Let’s start by defining the notion of a stable-point for [p]:

$x$ is a stable-point for $[p] ≝ [p] ∈ x & ∀ y (y > x → [p] ∈ y)$ .

That is, $x$ thinks that $p$ , and so does every normative outlook in $x$ ’s improvement* set. So, no matter how much $x$ self-improves, she’ll never stop thinking that $p$ . Likewise:

$x$ is a stable-point for not- $[p] ≝ [p] ∉ x & ∀ y (y > x → [p] ∉ y)$ .

That is, $x$ does not think that $p$ , and nor does any normative outlook in $x$ ’s improvement* set. So, no matter how much $x$ self-improves, she’ll never come to think that $p$ . Finally:

$x$ is an unstable-point for $[p] ≝ ∀ y ($ $(y = x ∨ y > x)$ →
( $([p] ∈ y → ∃ z (z > y & [p] ∉ z)) & ([p] ∉ y → ∃ z (z > y & [p] ∈ z))))$ .

That is, for every normative outlook $y$ in $x$ ’s improvement* set: if $y$ thinks that $p$ , then there is an outlook accessible from $y$ that does not think that $p$ ; and if $y$ does not think that $p$ , then there is an outlook accessible from $y$ that does. So, no matter how much $x$ self-improves, there is a further self-improvement that will lead her to change her mind.

These properties are mutually exclusive. And they are improvement*-stable, in the following sense: if a normative outlook $x$ instantiates one of these properties, every outlook in $x$ ’s improvement* set instantiates the same property.

While the properties are not jointly exhaustive—it is possible for a normative outlook to be neither a stable-point for $[p]$ nor a stable-point for not- $[p]$ without thereby being an unstable-point for $[p]$ —they are improvement*-exhaustive, in the following sense. For any normative outlook $x$ and any normative judgement $[p]$ , $x$ is not an unstable-point for $[p]$ iff there is either a stable-point for $[p]$ or a stable-point for not- $[p]$ in $x$ ’s improvement* set. In other words, if $x$ is not an unstable-point for $[p]$ , while that does not entail that $x$ itself is a stable-point either for $[p]$ or for not- $[p]$ , it does entail that there is such a stable-point accessible from $x$ .^²⁰ So, any improvement* set whatsoever must contain either a stable-point for $[p]$ or a stable-point for not- $[p]$ , or else will consist solely of unstable-points for $[p]$ .

The properties are not, however, improvement*-exclusive: there is no contradiction in supposing that there is a stable-point for $[p]$ , $a$ , a stable-point for not- $[p]$ , $b$ , and an unstable-point for $[p]$ , $c$ , accessible from the same normative outlook, $x$ . The improvement* sets of $a, b$ , and $c$ must be (i) disjoint and (ii) subsets of $x$ ’s improvement* set. But there is no contradiction in supposing that a set contains disjoint sets as proper subsets.

So, to summarise, for any normative outlook $x$ and normative judgement $[p]$ , the following options are jointly exhaustive, but not mutually exclusive:

There is a stable-point for $[p]$ in $x$ ’s improvement* set.
There is a stable-point for not- $[p]$ in $x$ ’s improvement* set.
There is an unstable-point for $[p]$ in $x$ ’s improvement* set.

Moving forward, I’ll suppress possibility (C). This is just to simplify presentation. Improvement* sets that contain unstable-points are special cases of possibilities I discuss below (see fn. 22). Enthusiasts can consult fn. 46 for discussion.

2.2.2. Favouritism

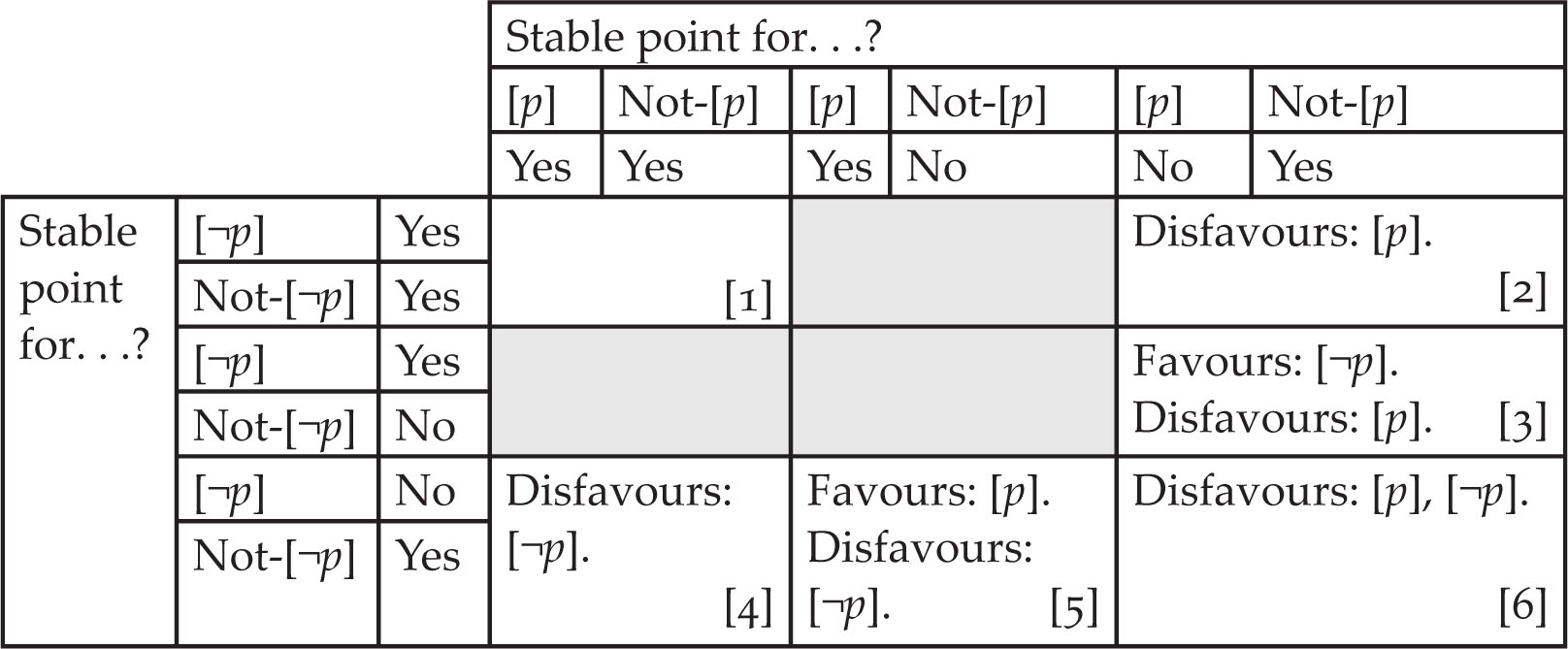
Setting aside (C), for any normative outlook $x$ and normative judgement $[p]$ , either there is a stable-point for $[p]$ in $x$ ’s improvement* set, or a stable-point for not- $[p]$ , or both.

What goes for $[p]$ goes for the contradictory judgement [ $¬ p]$ . So, looking at both a judgement $[p]$ (the columns) and its contradictory judgement [ $¬ p]$ (the rows), we get nine possibilities, represented by the cells in Table 1.

Table 1.

Three of these cells are greyed out. This comes from our second (and final) simplifying assumption: that for any normative judgement $[p]$ and its contradictory $[¬ p]$ , there is no outlook that is a stable-point for both $[p]$ and $[¬ p]$ . This is also just to simplify presentation—enthusiasts are once more directed to fn. 46.

(To see this, take the left cell on the centre row, and suppose our improvement* set is $X$ . By assumption, there is a stable-point for $[p]$ in $X$ —call it $y$ , and its improvement* set, $Y$ . Since accessibility is transitive, $Y$ is a subset of $X$ . Given that there is no unstable-point for $[¬ p]$ in $Y$ , there is either a stable-point for $[¬ p]$ or one for not- $[¬ p]$ in $Y$ . By assumption, however, there is no stable-point for not- $[¬ p]$ in $X$ , and so a fortiori none in $Y$ . So, there must be a stable-point for $[¬ p]$ in $Y$ —call it, $z$ . But since $z$ is accessible from $y$ and $y$ is a stable-point for $[p]$ , it follows that $z$ is a stable-point for $[p]$ and $[¬ p]$ . Similar reasoning runs for the centre cell on the top row and the centre cell of the centre row. So, if no pair of contradictory judgements has such a stable-point, then these three possibilities are ruled out.)

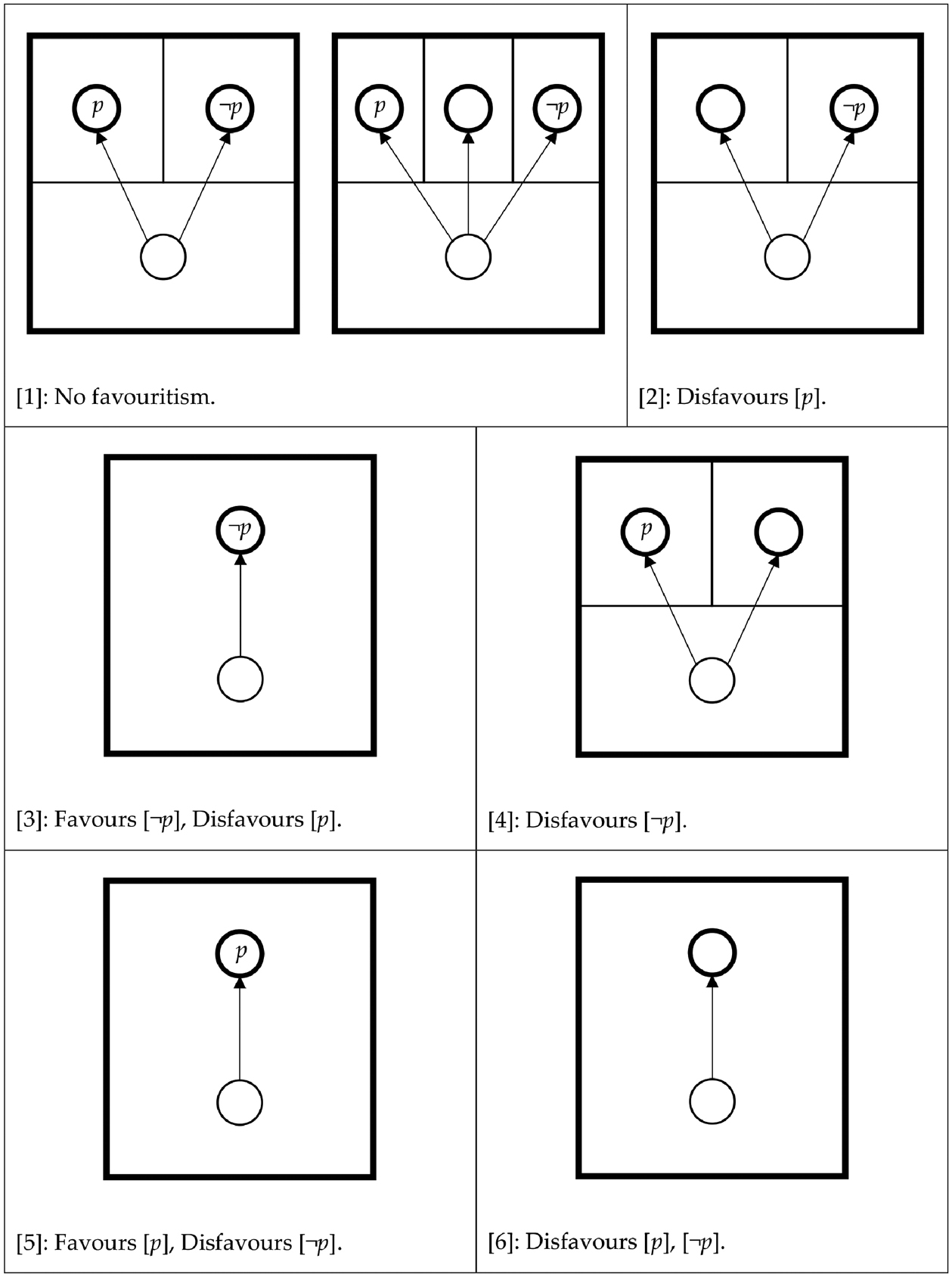
We’re left with six possibilities, represented by the other cells in the table. It’s helpful to represent these possibilities diagrammatically (Figure 1). Figure 1 is interpreted as follows. The bottom circle represents a normative outlook and the bold, external box its improvement* set. The arrows represent the accessibility relation, and the bold circles the kinds of stable-point accessible from that normative outlook. A “ $p$ ” in the bold circle means it’s a stable-point for $[p]$ and not- $[¬ p]$ ; a “¬ $p$ ” means it’s a stable-point for $[¬ p]$ and not- $[p]$ ; and an empty bold circle is a stable-point for not- $[p]$ and not- $[¬ p]$ . The internal boxes represent the disjoint improvement* sets of the stable-points represented.

Now, certain improvement* sets seem to “favour” or “disfavour” different normative judgements, depending on what kinds of stable-point one can reach via self-improvement. Consider [5]. Self-improvement can only lead you to a stable-point for $[p]$ ; it cannot lead you to a stable-point for not- $[p]$ . In this sense, it favours $[p]$ . By contrast, self-improvement can only lead you to a stable-point for not- $[¬ p]$ ; it cannot lead you to a stable-point for $[¬ p]$ . In this sense, it disfavours $[¬ p]$ .

Contrast this with, say, [2]. Self-improvement can only lead you to a stable-point for not- $[p]$ , it cannot lead you to a stable-point for $[p]$ . So, it disfavours $[p]$ . However, self-improvement can either lead you to a stable-point for $[¬ p]$ , or to a stable-point for not- $[¬ p]$ . So it neither favours nor disfavours $[¬ p]$ .

We can render this idea precise by saying that a set of normative outlooks $X$ favours $[p]$ iff, for every outlook $x$ in $X$ , there is a stable-point for $[p]$ , $y$ , that is either accessible from or identical to $x :$

A set of normative outlooks $X$ favours $[p] ≝ ∀ x (x ∈ X → ∃ y ($ $(y > x ∨ y = x) & ∀ z ($ $(z > y ∨ z = y) → [p] ∈ z)))$ .

And $X$ disfavours $[p]$ iff, for every outlook $x$ in $X$ , there is a stable-point for not- $[p]$ , $y$ , that is either accessible from or identical to $x :$

A set of normative outlooks $X$ disfavours $[p] ≝ ∀ x (x ∈ X → ∃ y ($ $(y > x ∨ y = x) & ∀ z ($ $(z > y ∨ z = y) → [p] ∉ z)))$ .

Intuitively, a set of outlooks (dis)favours a normative judgement $[p]$ iff every outlook in that set either is a stable-point for (not-) $[p]$ , or could reach a stable-point for (not-) $[p]$ via self-improvement.

2.3. The Significance of Favouritism

Our discussion thus far has been abstract. We’re now in a position to consider its philosophical significance.

2.3.1. Undermining Normative Inquiry

For the expressivist, to engage in normative inquiry is to try to self-improve. But it seems, at first blush, that one’s reliance on self-improvement as a means for answering normative questions would be undermined if your improvement* set exemplified some of the structures laid out above.

Consider [1]: self-improvement can lead you to a stable-point for $[p]$ , but can also lead you to a stable-point for $[¬ p]$ . If this were so, then engaging in normative inquiry would seem pointless, as far as coming to a decision on this matter is concerned.^²¹ The process could as much lead to one verdict as another. So why bother? You might as well flip a coin.

Or consider [6]: self-improvement cannot lead you to either a stable-point for $[p]$ , or a stable-point for $[¬ p]$ . As we put it above, self-improvement disfavours making a judgement one way or the other.^²² But the whole point of engaging in normative inquiry is to try and come to a verdict one way or the other.

2.3.2. Indeterminacy

There are, however, cases in which we arguably should not expect normative inquiry to issue in a verdict one way or the other: cases of indeterminate normativity.

For example, to get your attention, it’s clearly morally permissible, in the normal run of things, to tap your shoulder. It’s clearly morally impermissible to punch your shoulder. The difference between a tap and a punch is, let’s suppose, a matter of force. But exactly how much force is too much? Trying to find a precise cut-off here is like trying to find a precise cut-off between red and orange. Moral permissibility is vague: tapping is clearly permissible, punching clearly impermissible, but between the two there is a “zone of indeterminacy”, a set of borderline cases, which are neither clearly permissible nor clearly impermissible.^²³

Suppose that φ-ing is one such borderline case. What is distinctive of the uncertainty engendered by indeterminacy is precisely that it does not seem resolvable, even in principle, through further inquiry. When faced with a borderline reddy-orangey colour swatch, no further information could help you figure out whether it is red or orange. You already have all the relevant information. The information just doesn’t warrant a verdict one way or the other. Likewise, our uncertainty as to whether φ-ing is permissible does not feel like it is resolvable through further inquiry.

So, if a normative matter is indeterminate, arguably we should not expect normative inquiry to issue in a verdict one way or the other. On the contrary, it’s plausible that normative inquiry should disfavour forming an opinion one way or the other (as in [6]); or at least shouldn’t favour either verdict (as in [1]).^²⁴

2.3.3. Higher-Order Indeterminacy

Between tapping and punching, we’ve said, is a zone of indeterminacy: cases that are neither clearly permissible, nor clearly impermissible. But where, exactly, does this zone of indeterminacy begin? Finding a precise cut-off here—between the cases that are clearly permissible and those that are not clearly permissible—is no easier than finding the original cut-off. This creates a second-order zone of indeterminacy, between the clearly permissible and the not clearly permissible.

Suppose that ψ-ing falls into this second-order zone: (i) ψ-ing is not clearly clearly permissible, and (ii) ψ-ing is not clearly not clearly permissible. Given this, it’s plausible that normative inquiry should neither favour nor disfavour the judgement [ψ-ing is permissible].

However, ψ-ing is clearly not clearly impermissible. If ψ-ing were clearly impermissible, then ψ-ing would clearly not be clearly permissible, contradicting (ii). So normative inquiry should disfavour [ψ-ing is not permissible].

This is exactly the structure found in [4]. An improvement* set with this structure disfavours [ψ-ing is not permissible] without favouring or disfavouring [ψ-ing is permissible].

Analogous reasoning runs at the other end of the zone of first-order indeterminacy, concerning the cut-off between what is clearly impermissible and what is not clearly impermissible. If χ-ing falls into this zone of second-order indeterminacy, then arguably normative inquiry should neither favour nor disfavour [χ-ing is not permissible], while disfavouring [χ-ing is permissible]. This is the structure found in [2].^²⁵

2.3.4. Determinacy and Favouritism

So, one’s reliance on self-improvement as a means for answering normative questions is compatible with your improvement* set having structure [1], [2], [4], or [6] if the matter is indeterminate, at some order of indeterminacy. But if there is a determinate fact of the matter, it would be undermined. Since engaging in normative inquiry typically presupposes that there is determinate fact of the matter, you are implicitly relying on your improvement* set having structure [3] or [5]; that is, either favouring $[p]$ , or favouring $[¬ p]$ .

Moreover, one’s reliance on self-improvement would be undermined if your improvement* set favoured $[p]$ when it is (determinately) not the case that $p$ ; or if your improvement* set favoured $[¬ p]$ when it is (determinately) the case that $p$ . As we’ll discuss more below, this amounts to a kind of sceptical scenario, where successful engagement in normative inquiry leads you to the determinately wrong answer.

2.4. A Theory of Normative (In)Correctness

Drawing on the above, we can offer a non-representational theory of normative (in)correctness that vindicates the nature of normative inquiry as the expressivist conceives of it and should therefore be attractive to the expressivist. For the time being, I’ll put an implausible emphasis on my own normative outlook $w$ and improvement* set $W$ . I’ll amend this later in the light of the Smugness Objection. But the following captures the structure of the proposal:

Normative (In)Correctness (W-centric)

It is determinately correct to believe that $p$ iff $W$ favours $[p]$ .
It is determinately incorrect to believe that $p$ iff $W$ favours $[¬ p]$ .

Two related observations. First, this proposal has important consequences for the extension of indeterminate normativity. From:

It is determinately correct to believe that $p$ iff it is determinately the case that $p$ ,

and:

It is indeterminate whether $p$ iff it is not determinately the case that $p$ and it is not determinately the case that not- $p$ ,

it follows:

It is indeterminate whether $p$ iff it is not determinately correct to believe that $p$ and not determinately correct to believe that not- $p$ .

So from Normative (In)Correctness (W-centric), it follows:

It is indeterminate whether $p$ iff $W$ does not favour $[p]$ and $W$ does not favour $[¬ p]$ .^²⁶^,^²⁷

Second, this is strictly speaking a theory of determinate normative (in)correctness. If we drop the reference to determinacy, we get: if it is indeterminate whether $p$ , then it is incorrect to believe that $p$ . That’s not implausible, but it is a substantive commitment (see fn. 24) that we don’t need. Instead, we’re only committed to: if it is indeterminate whether $p$ , then it is not determinately correct to believe that $p$ .

3. Objections

We’ve developed a non-representational theory of normative (in)correctness that should be attractive to the expressivist. However, the proposal faces two interrelated objections regarding normative fallibility: the Limited Fallibility Objection and the Smugness Objection. I’ll discuss these in turn, before responding to a third objection that arises from the response to the second.

3.1. The Limited Fallibility Objection

Objection. Our non-representational theory of normative (in)correctness enables me to make sense of my own normative fallibility. While I think that eating meat is wrong, I might be mistaken, since my improvement* set might favour [eating meat is not wrong]. This is, in effect, a sophisticated version of the Instability Proposal. However, this gives me no way of making sense of the possibility that my improvement* set favours a mistaken normative judgement. However unlikely I take this to be, the suggestion looks coherent. So we ought to be able to make sense of it. But it looks like we have no way of doing so. This is the Limited Fallibility Objection.^²⁸

Response. Expressivism is a rival to metanormative views like non-naturalist and naturalist realism, constructivism, and error theory. Now, suppose (i) that we can make sense of the possibility that some other metanormative view is correct, and (ii) that at least one such view does not imply that it is correct to believe that $p$ iff my improvement* set favours $[p]$ . If, for instance, non-naturalist realism is true, then there is a sui generis realm of normative facts, and there is no obvious a priori guarantee that the judgements favoured by my improvement* set will line-up with them. It follows that, if expressivism is not true, then it may be incorrect to believe that $p$ , even if my improvement* set favours $[p]$ . The expressivist, we’re supposing, denies the consequent of this conditional; but she can nonetheless affirm the conditional itself, since she also denies its antecedent. So the expressivist can make sense of the possibility that not- $p$ , even if her improvement* set favours $[p]$ —she does so conditional on the assumption that some other metanormative view than her own is correct.^²⁹

(Assumptions (i) and (ii) are eminently plausible. And if either fails, this would make the Limited Fallibility Objection everyone’s problem: either because, contra (i), there are no rival metanormative views; or because, contra (ii), every such rival implies that it is correct to believe that $p$ iff my improvement* set favours $[p]$ . Indeed, it is enough that it is coherent to think that there could be a rival metanormative view that doesn’t have this consequence, whether or not there are any.)

So the objection is only pressing if we suppose that I ought to be able to make sense of the possibility that my improvement* set favours a mistaken normative judgement even on the assumption that expressivism is true. But it’s hard to see why the expressivist should acknowledge this as a legitimate constraint. The envisaged possibility is a sceptical scenario, where even my best efforts to uncover the normative truth will lead me astray. Taking this possibility seriously would therefore undermine ordinary normative inquiry. Given that the expressivist aims to vindicate everyday normative practice, it is other things equal a good-making feature of her theory if it rules out such sceptical possibilities.^³⁰

3.2. The Smugness Objection

3.2.1. The Objection

The $W$ -centric account of normative (in)correctness rules out the possibility that my improvement* set favours a determinately incorrect normative judgement. It thus rules out that I’m in a certain kind of sceptical scenario. But it doesn’t rule out that you are in such a scenario. Suppose that my improvement* set favours $[¬ p]$ , but yours favours $[p]$ . Following the literature, we’ll say that we fundamentally disagree. (Note that “fundamental disagreement” so understood is a term of art; it may not track its use in other contexts.) It follows from the $W$ -centric account that your improvement* set favours a determinately incorrect normative judgement. In this sense, you are vulnerable to a kind of error to which I am immune. But taking my normative outlook to be special just because it is mine would surely be arbitrary and self-aggrandising. This is the Smugness Objection.^³¹

Extant attempts to meet the Smugness Objection in the literature are inadequate.^³²

Lenman (2014) dramatizes the possibility of fundamental moral disagreement by imagining “The Others”, a community with whom we fundamentally disagree: “The Others live on a distant planet in a remote galaxy and, while they are recognizably rational creatures, while indeed they are really rather clever, their moral beliefs are, by our lights, immensely alien and strange and perhaps rather horrible” (2014: 242–43). Lenman says that he doesn’t want “smugly to affirm that they are wrong and [he is] right” because he doesn’t “see the point of saying anything of the sort” (2014: 243). His claim seems to be that the concept of being right or wrong about a moral matter only applies to “those with whom I seek to live in moral community […] a local problem to which the distant and alien Others have no relevance” (2014: 243).

I find this hard to understand. There’s a danger of being misled by the dramatization. Perhaps we can shrug off The Others as “don’t cares” as long as they stay isolated in their distant galaxy. But that is utterly contingent—what if they warp to Earth? If we are forced to live in a moral community with them, Lenman’s response cannot get a grip. And even while they are distant, insofar as we disagree with The Others’ moral judgements, aren’t we (relativism aside)^³³ committed to thinking that at least one of us must be in the wrong? And even if we’re happy shrugging off The Others, what to say about fundamental moral disagreement here on Earth?^³⁴

Horgan and Timmons (2015: 202–3) observe that it is often thought to be rationally permissible to stick with your own judgement when disagreeing with a peer. They take this to imply that it is rationally permissible—and hence not “unpardonably smug”—to privilege your own judgement in cases of fundamental disagreement. But this fails to speak to the worry. Even if it is rationally permissible to retain my judgement when I fundamentally disagree with a peer, I should still allow that it could be the case that she is right and I am wrong. The Smugness Objection targets my inability to do so. Nothing Horgan and Timmons (2015: 202–4) say in their response speaks to this worry.^³⁵

Ridge (2015) explains how to make sense of the possibility that one of my judgements is stable—in the sense that it would survive arbitrary self-improvement—and yet still could be mistaken. It seems coherent to think this pen would fall, if dropped, but also that it could fail to fall. Ridge suggests this is because the semantics of “would” is only sensitive to nearby possible worlds, while “could” is sensitive to all epistemically possible worlds. Even if the pen falls in all nearby worlds, as long as I am not certain it will fall, there is an epistemically possible world in which it does not fall. Similarly, Ridge argues, it is coherent to think that my judgement $[p]$ would survive arbitrary self-improvement, but also that it could fail to do so.^³⁶ If so, it is coherent to think that my judgement is stable, and yet could be mistaken.

Now, if it could be the case that one of my judgements is both stable and mistaken, then my stable judgements are not immune from error, meaning there is no asymmetry between you and me on this front. However, Ridge has not explained why it is coherent to think that it could be that my judgement is both stable and mistaken—a thought of the form ‘could $(p & q)$ ’. He has explained why it is coherent to think that my judgement is stable and yet could be mistaken—a thought of the form ‘ $p$ & could $(q)$ ’. The coherence of the former thought does not follow from the coherence of the latter. It makes sense to think that this pen would fall, but could fail to fall, because there is a distant world in which it does not fall; but it doesn’t make sense to think that this pen could both fall and not fall—that requires a world in which it both does and doesn’t fall. Likewise, for Ridge it makes sense to think that my judgement would survive arbitrary self-improvement, but could be mistaken, because there is a distant world in which it doesn’t survive self-improvement; but then it doesn’t make sense to think my judgement could be both stable and mistaken—that requires a world in which it both does and doesn’t survive self-improvement. So I cannot make sense of the idea that my judgement could be both stable and mistaken.^³⁷ But I can make sense of the idea that one of your judgements could be both stable and mistaken. The asymmetry stands.

Finally, Bex-Priestley (2018) argues that the expressivist should be willing to embrace the “smugness”, arguing that doing so is not revisionary of ordinary moral thought and talk, and that it amounts to a kind of transcendental argument against radical moral scepticism.

Bex-Priestly is, I think, half-right. Any normative outlook $x$ is either (i) better than mine, by my own lights; (ii) worse than mine, by my own lights; or (iii) no better or worse than mine, by my own lights. If (i), then $x$ is in my improvement* set, and the question of smugness does not arise. But what about (ii)? Suppose that your outlook is less informed, less sensitive, less imaginative, less mature, less coherent, and consequently worse than mine, by my lights. I therefore have principled grounds for thinking that you might be vulnerable to a kind of error to which I am immune. What privileges my normative outlook over yours is not the arbitrary feature that it’s mine. It’s that it is more informed, more sensitive, more imaginative, more mature, more coherent. These are, by my lights, exactly the kinds of features that put one in a better epistemic position. So there would be nothing arbitrary or smug about thinking on these grounds that there could be an asymmetry between us. Of course, in saying this I am expressing my own (higher-order) normative views. But there’s nothing smug about that.

But now suppose your outlook is no better or worse than mine, by my lights. Perhaps our outlooks are equally good,^³⁸ or perhaps my higher-order normative judgements render no verdict on the matter. (For instance, if I am better informed, but you are more coherent, and my higher-order norms don’t include any precise way of trading these off.) I therefore have no non-arbitrary grounds for thinking that you might be vulnerable to a kind of error to which I am immune. By my own lights, there can be other, perfectly reasonable starting points for normative inquiry besides my own. Contra Bex-Priestley, we cannot embrace the asymmetry across the board.

3.2.2. The Response

Call my improvement* set $W$ and your improvement* set $V$ . The asymmetry arises because the $W$ -centric account of normative (in)correctness appeals to the judgements favoured by $W$ , not $V$ ; and our improvement* sets may favour different judgements. A $V$ -centric account would be just as bad. To eliminate the asymmetry, we need to take the stable-points accessible from your normative outlook just as seriously as the stable-points accessible from mine.

It’s straightforward to do so. Take the union of our improvement* sets, ${W ∪ V}$ , and replace all occurrences of $W$ in our account of normative (in)correctness with ${W ∪ V} :$

Normative (In)Correctness (W-and-V-centric)

It is determinately correct to believe that $p$ iff ${W ∪ V}$ favours $[p]$ .
It is determinately incorrect to believe that $p$ iff ${W ∪ V}$ favours $[¬ p]$ .

Any asymmetry between us is eliminated. ${W ∪ V}$ favours $[p]$ iff $W$ favours $[p]$ and $V$ favours $[p]$ . So it is determinately correct to believe that $p$ iff $[p]$ is favoured by both our improvement* sets; and it is determinately incorrect to believe that $p$ iff $[¬ p]$ is favoured by both our improvement* sets. In any other eventuality, including cases of fundamental normative disagreement, it is neither determinately correct nor determinately incorrect to believe that $p$ . So, your improvement* set can either favour, disfavour, or neither favour nor disfavour a normative judgement that is not determinately correct; and so can mine. Neither of us is advantaged or disadvantaged. Here, then, is the strategy for answering the Smugness Objection: generalise this smugness-barring move to eliminate the problematic asymmetry wherever it arises.

The difficult question concerns how far we need to extend the generalisation. Let’s say that a normative outlook $x$ is reasonable only if it is not the case that any judgement favoured by $x$ ’s improvement* set is determinately incorrect. Our question, then, is which normative outlooks we should consider reasonable.

Now, I have a substantive view on this matter. In responding to Bex-Priestley, I argued (i) that it would be arbitrary to think that my outlook is reasonable and yours is not if yours is no worse than mine by my own lights, but (ii) that I would have principled grounds for thinking that your outlook might be unreasonable if it is worse than mine by my lights. Since I’m committed to my own outlook being reasonable, it follows that $x$ is reasonable if $x$ is no worse than my outlook (by my lights). So, by extending the smugness-barring move to include all those outlooks no worse than mine by my lights, our theory of normative (in)correctness would only imply an asymmetry between those outlooks no worse than mine by my lights and those that are worse than mine by my lights. And this asymmetry, I’ve argued, is principled, not arbitrary.

However, I ought to allow for the possibility that I am currently mistaken about which normative outlooks are reasonable. After all, which normative outlooks I consider reasonable is determined by which higher-order norms I endorse. This suggests that which normative outlooks are reasonable is itself a normative question; i.e. that $[x$ is reasonable] is a normative judgement. My own view is that $x$ is reasonable if $x$ is no worse than my outlook (by my lights). But I could be mistaken.

Let’s say that a normative outlook $x$ is favoured by a set of normative outlooks $S$ (or S-favoured) iff $[x$ is reasonable] is favoured by $S$ . For instance, if my judgement that your outlook $v$ is reasonable would survive arbitrary self-improvement, then $v$ is favoured by my improvement* set $W$ , or $W$ -favoured. So the $W$ -favoured outlooks are not merely those I happen to think are reasonable right now, but those that successful normative inquiry would lead me to believe are reasonable. Plausibly, then, I ought to generalise the smugness-barring move to just the $W$ -favoured outlooks. That is, where $W *$ is the union of the improvement* sets of the $W$ -favoured outlooks:^³⁹

Normative (In)Correctness (W*-centric)

It is determinately correct to believe that $p$ iff $[p]$ is favoured by $W *$ .
It is determinately incorrect to believe that $p$ iff $[¬ p]$ is favoured by $W *$ .

This renders the Smugness Objection unstable: the objector must argue that some outlook $x$ is reasonable but not $W$ -favoured, or $W$ -favoured but not reasonable. But any compelling argument that $x$ is reasonable is an argument that I ought to accept $[x$ is reasonable], and thus an argument that $x$ is $W$ -favoured; and any argument that $x$ is not reasonable is an argument that I ought not to accept $[x$ is reasonable], and thus that $x$ is not $W$ -favoured.

What if there is fundamental disagreement about which outlooks are reasonable?^⁴⁰ In such a case, there are three outlooks in play: the two that fundamentally disagree— $w$ and $v$ , say—and the outlook whose reasonableness is at issue—call it, $a$ . Suppose that [ $a$ is reasonable] is favoured by $W$ , but [ $a$ is not reasonable] is favoured by $V$ .

If $v$ is itself $W$ -favoured, then $W$ and $V$ are both subsets of $W *$ ; so, $[a$ is reasonable] is neither favoured nor disfavoured by $W *$ . It follows that it is indeterminate whether $a$ is reasonable; so, there is no asymmetry between $w$ and $v$ . (Indeterminacy about reasonableness seems unobjectionable—there is no reason that there should be a sharp cut-off between the reasonable and unreasonable normative outlooks.)^⁴¹

If $v$ is not $W$ -favoured, then it may be the case that it is determinately correct to believe that $a$ is reasonable, even though $v$ ’s improvement* set favours [ $a$ is not reasonable]. But since successful normative inquiry will not lead me to believe that $v$ is reasonable, this is just an instance of the principled asymmetry I’ve argued the expressivist should be willing to embrace. So, no distinct problem is posed by fundamental disagreement about which outlooks are reasonable.

3.3. The Proliferation Objection

Objection. If two reasonable outlooks fundamentally disagree, it follows on the proposed account that the matter is indeterminate. This removes any implausible epistemic asymmetry between reasonable outlooks. But we might worry that the proposal hereby proliferates indeterminate normativity to an unacceptable extent. Call this the Proliferation Objection.

It’s hard to press the Proliferation Objection by pointing to a particular case of fundamental disagreement and insisting that there must be a determinate fact of the matter about that. While postulating indeterminacy arguably undermines the significance of the dispute, the very fact that there is an irresolvable disagreement between reasonable normative outlooks provides some reason to think the matter indeterminate;^⁴² and by the expressivist’s lights, there is no antecedently given normative ontology that could determine the matter one way or the other.

The Proliferation Objection is most pressing if we assume that there is widespread fundamental normative disagreement about important topics—such as vegetarianism, abortion, euthanasia, the death penalty, torture, trolley cases, and so on. Widespread indeterminacy would undermine vast swathes of ordinary normative discourse.^⁴³

Response. It is not clear that there is widespread fundamental normative disagreement; and if there is, this would already undermine ordinary normative discourse—the accompanying proliferation of indeterminacy doesn’t make matters worse.

To be a stable-point for $[p]$ , it is not sufficient that you will not, in fact, change your mind; nor even that you could continue to self-improve indefinitely without ever changing your mind. It requires that you cannot change your mind through self-improvement. Now, perfectly reasonable, intelligent people believe that eating meat is permissible; and they have good arguments for their views that are hard to dislodge. Nonetheless, I suspect that the judgement is always ultimately due to shortcomings of information, sensitivity, coherence, and the like, and that proper reflection would—or, at least, could—lead dissenters to change their minds. If I didn’t think this—if I thought that a reasonable interlocutor could hold this judgement without any such shortcomings, such that she could not, even in principle, come to change her mind through successful normative inquiry—then I would and should be correspondingly less confident that my own judgement is determinately correct after all. To this extent, in taking a stance on a normative matter I’m committed to thinking that any disagreement with a reasonable interlocutor is not fundamental.^⁴⁴

But suppose that we do fundamentally disagree about the permissibility of eating meat; and suppose that there is a determinate fact of the matter. So, either my improvement* set favours a determinately incorrect normative judgement, or yours does. Suppose it is mine. It follows that I cannot come to the correct judgement on this matter by successfully engaging in normative inquiry. I am in a kind of sceptical scenario. (You might wonder how you could ever know that you’re not the one in the sceptical scenario. So perhaps you’re in a sceptical scenario too.) If there is widespread fundamental normative disagreement, such sceptical scenarios will be correspondingly widespread. Now, the representationalist-realist is entitled to this diagnosis of the situation, where the expressivist is not. But this hardly seems like an advantage. Other things equal, the sceptical conclusion that perfectly reasonable normative agents are often hopelessly isolated from the determinate normative truth looks less appealing than the diplomatic, anti-sceptical conclusion that denies this.^⁴⁵

The realist may respond that she can resist the sceptical conclusion, because she is entitled to extra resources: the realist can and should concede that we make higher-order normative judgements that guide the formation and maintenance of our normative outlooks (while disagreeing with the expressivist about the nature of such judgements), but the realist can also postulate an occult faculty of “intuition” or “perception” that we use to detect the normative facts. If you’re happy with that, you might think this faculty can guide us to the truth when self-improvement fails. But suffice it to say that the expressivist will not be impressed by any claim to dialectical advantage that makes use of such dubious resources.^⁴⁶

4. Conclusion

If, as expressivists contend, normative thought and talk does not function to represent the world, it is puzzling how there can be correct or incorrect normative judgements. I have argued here for a non-representational theory of normative (in)correctness, which explains what it is for a judgement to be (determinately) correct in terms of its stability through successful normative inquiry. I have argued that this proposal vindicates the nature of normative inquiry as the expressivist conceives of it, leaves sufficient room for my own fallibility, and does not imply a problematic asymmetry between my outlook and others. I conclude with two important clarifications.

First, we should not confuse this account of what makes the judgement [eating meat is wrong] correct with an account of what makes eating meat wrong.^⁴⁷ The latter is a first-order normative issue. What makes eating meat wrong, if indeed it is, is the impact of animal husbandry on the environment and the animals, etc., not anything to do with the stability of the corresponding judgement under improvement. We should only amalgamate the questions if we endorse a deflationary account of normative correctness, and this is exactly what we are not doing if we go for the theory of normative (in)correctness developed here.

Second, this is a theory of correctness for normative judgements, not a theory of truth for normative sentences. It is natural to extend the account, by explaining sentential truth in terms of the expression of correct judgements. Indeed, I am optimistic that the expressivist will be able to “earn the right” to a truth-conditional semantics for normative discourse on this basis. But this is an extension of the project, and not something I’ve defended here.

Acknowledgements

Enormous gratitude to Daniel Elstein, without whose inexhaustible support this paper wouldn’t have been possible (though I bear full responsibility for the remaining blunders). Thanks also to audiences at the University of Leeds and the University of Bologna for comments on and discussion of earlier versions, and to two anonymous referees for Ergo. The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Research Framework (FP\2007–2013)/ERC Grant Agreement No. 312938; and from the British Academy (Grant No. PF2\180082).

Notes

Paradigms include Ayer (1936: ch. 6), Stevenson (1944), Blackburn (1984; 1993; 1998), Gibbard (1990; 2003), and Ridge (2014). “Normative judgement” is here a neutral term for the mental state expressed by an atomic declarative normative sentence. ⮭
Assuming the expressivist can make sense of normative disagreement. Cf. Stevenson (1944: ch. 1), Baker and Woods (2015). Compare Egan (2007: 209) on “third-personal” error. ⮭
See also Köhler (2015), Beddor (2020), and Lam (2020). ⮭
Besides denying the presupposition that there are (in)correct normative judgements (Ayer 1936: 110–11). Failure to explicitly distinguish these responses often complicates discussion. Early Blackburn (e.g., 1984: ch. 6), for instance, is plausibly construed as pursuing strategy (1). Egan (2007) seems to construe Blackburn’s (1998: 318) later statement in this way too. Part of Blackburn’s (2009: 207) response is that he is in fact interested in strategy (3). Köhler (2015) rightly points out that Egan’s Smugness Objection recurs when Blackburn is interpreted this way. ⮭
I avoid the label ‘quasi-realism’ to avoid confusion. Despite Blackburn coining the term before being convinced by deflationism (e.g., Blackburn 1984), deflationism is sometimes taken to be essential to quasi-realism. As highlighted here, this is just one (prominent) approach. ⮭
See Dunaway (2010) for a presentation of the “general minimalist strategy”. ⮭
E.g., synonymy, or at least analytical, conceptual, or cognitive equivalence. See, e.g., Ayer (1936: 85–86), Field (1994: 405), Horwich (1998: 4–5). ⮭
Incidentally, this shows that discussions of the “Problem of Creeping Minimalism” (cf. Dreier 2004)—which maintains that minimalism makes it hard to distinguish expressivism from realism—often move too quickly. From the fact that the expressivist is entitled to say that there are normative facts, it does not follow that she can use such facts to all the explanatory ends to which the realist can use them. Indeed, we’ve just seen that minimalism can be a hindrance to this end. ⮭
Cf. Blackburn (2009: 207): “What I do offer is an account of […] the state of mind of worrying whether one is oneself in moral error […]. But if some theorist bent on finding truth-conditions asks me what my account of moral error itself is, then I am not very forthcoming.” ⮭
We’re in preface paradox territory, but it seems I can also coherently think that some of my normative judgements are mistaken, if I remain agnostic about which ones. ⮭
This way of understanding the Instability Proposal comes with its own difficulties, however—see Beddor (2020: 2–3) on the “Semantic Plausibility” difficulty (cf. Schroeder 2013: 416). By developing the Instability Proposal as a part of strategy (1), I remain neutral on the answer to the “sideways-on” question. My proposal can, for instance, be combined with Beddor’s quite different answer. ⮭
It’s surprising that the literature is so focused on this short passage, which crops up in passing in the appendix to a book. The Instability Proposal has been a part of Blackburn’s view for half a century (e.g., Blackburn 1971: 122–23) and has been developed at greater length elsewhere (e.g., Blackburn 1984: 198–202). Precursors are found in, e.g., Peirce (1878) and Putnam (1981). ⮭
While I follow Blackburn in using higher-order norms to make sense of normative fallibility in particular, the overall picture owes more to Gibbard’s development of the expressivist project, which makes substantial use of higher-order norms—see especially Gibbard (1990: chs. 8–13). ⮭
I implicitly assume that these facts are non-normative, which may be controversial. “Sensitive”, “imaginative”, and “mature” in particular are plausible examples of thick normative predicates, and it is controversial whether thick predicates are evaluative as part of their semantic content, or convey evaluative content by some pragmatic mechanism (Väyrynen 2019). The former is in tension with taking facts about the sensitivity, imaginativeness, maturity of normative outlooks for granted in this context; the latter—which Blackburn (1992; 2013) himself favours—is not. Since the expressivist is unlikely to be able to use higher-order normative judgements to account for normative inquiry unless they are generally concerned with non-normative features, for present purposes I work with the substantive but plausible assumption that this is so, using Blackburn’s examples as stand-ins for these non-normative features. ⮭
This is why I focus on normative judgements in general, rather than moral judgements in particular. ⮭
Gibbard (1990: 170ff) sometimes talks this way, but is officially neutral (1990: 176, fn. 3). ⮭
For instance, it would be unclear how to make sense of the possibility that a highest-order normative judgement is mistaken. Perhaps, however, one could argue on precisely this basis that our highest-order normative judgements are “inescapable”; and leverage this into a transcendental argument in their favour. This is a theme in Gibbard (1990: 176–79). ⮭
This is, I think, Blackburn’s (2009: 206) view. ⮭
The asterisk highlights that your improvement* set consists of those outlooks accessible to you through what you take (at each stage) to be improving changes; rather than what in fact are improving changes. ⮭
Proof. For $x$ to be an unstable-point for $[p]$ , two conditions are individually necessary and jointly sufficient. (1) For every $y$ accessible from $x$ that thinks that $p$ , there is some $z$ accessible from $y$ that does not think that $p$ . This rules out that any $y$ accessible from $x$ is a stable-point for $[p]$ . (2) For every $y$ accessible from $x$ that does not think that $p$ , there is some $z$ accessible from $y$ that does think that $p$ . This rules out that any $y$ accessible from $x$ is a stable-point for not- $[p]$ . So, $x$ is an unstable-point for $[p]$ iff there is no stable-point for $[p]$ accessible from $x$ , and no stable-point for not- $[p]$ accessible from $x$ . ⮭
I hedge because self-improvement might have other benefits—e.g., your verdict might cohere nicely with your other views. Nonetheless, as far as this normative matter is concerned, flipping a coin seems as good as engaging in normative inquiry. ⮭
Similar reasoning would run if there is an unstable-point for $[p]$ accessible from your normative outlook, the possibility suppressed by our first simplifying assumption. This is a special case of [1], where neither $[p]$ nor $[¬ p]$ is favoured or disfavoured by your improvement* set. ⮭
If this example doesn’t convince you, there are others—as Williams (2017) stresses, not all instances of indeterminate normativity result from vagueness, and global scepticism is radical and unattractive. ⮭
[1] and [6] reflect different answers to the question of what attitude you ought to take towards normative $p$ when the matter is indeterminate: [6] that you should neither believe that $p$ nor believe that not- $p$ (but, say, have middling credence or suspend judgement); [1] that it is permissible to either believe $p$ or believe not- $p$ (cf. Williams 2014). ⮭
There are yet higher orders of indeterminacy, but these create no relevant complications. ⮭
In work-in-progress, I explore this expressivist-friendly approach to indeterminate normativity in much more detail, e.g., showing how it can be fleshed out to accord with different logics of indeterminacy (gappy, glutty, many-valued, classical-supervaluational), and different accounts of indeterminacy’s “cognitive role” (e.g., what attitude one ought to take towards indeterminate $p)$ . Such details can be set aside here. ⮭
Our second simplifying assumption ruled out improvement* sets that favour $[p]$ without disfavouring $[¬ p]$ and vice versa, including those that favour both $[p]$ and $[¬ p]$ . In the latter case, the present theory predicts that it is correct to believe that $p$ and correct to believe that $¬ p$ (akin to a normative dialetheia). I think this is just the right result in this far-fetched case; but if you want to rule it out, you can supplement the account of correctness with “… and $W$ does not favour $[¬ p]$ .” This entails that “ $p$ ” is indeterminate. ⮭
Cf. Blackburn (2009: 203–4). ⮭
See Horgan and Timmons (2015: 205–6) for a related response. ⮭
A similar point is made by Blackburn (1996) and Bex-Priestley (2018: 1062). ⮭
Egan (2007: 215–17). We can see this as a way of pressing the Limited Fallibility Objection: unless I make more room for my own fallibility, I’ll be guilty of smugness. ⮭
The literature typically focuses on the special case of what I’m calling fundamental disagreement, where my current outlook is a stable-point for $[p]$ , and yours a stable-point for $[¬ p]$ . It also typically focuses on moral disagreement. These details don’t impact the discussion. ⮭
Lenman (2014: 243) and Bex-Preistley (2018: 1060) hint at a relativistic response. Relativism is, I think, a live option; but to rein in discussion I’ll continue implicitly working in an absolutist framework. This is dialectically permissible: assuming absolutism makes the Smugness Objection more pressing. ⮭
Lenman (2014: 242) is optimistic that fundamental moral disagreement on Earth is rare. I’m sympathetic. Nonetheless, it’s possible; so we need to address it. ⮭
Ironically, the epistemological principle Horgan and Timmons appeal to makes the Smugness Objection more pressing, since it’s likely to make fundamental moral disagreement more common. Consider the rival “conciliationist” view: when disagreeing with a peer, you ought to suspend judgement. So, if $x$ and $y$ are peers that disagree, then by the lights of conciliationism, each could improve by suspending judgement. So for improvement* sets that favour conciliationism, there is pressure towards lack of disagreement on moral issues. But if an improvement* set does not favour conciliationism, this source of pressure disappears. ⮭
Assuming I am not certain that it is stable. What if I am certain? Ridge argues that such certainty is unreasonable, so I would already be guilty of an epistemic vice: “the fault here lies with the agent and not with the expressivist account of her judgement” (2015: 18). Perhaps so, but expressivism still seems to entail that I am guilty of a further epistemic vice—see Bex-Priestley (2018: 1059). ⮭
Bex-Priestley (2018: 1059–60) develops a different argument to the same conclusion. ⮭
Or stand in some further comparability relation, if such exists—e.g., Chang’s (2002) being on a par. ⮭
As long as my present normative outlook is $W$ -favoured, the $W *$ -favoured outlooks will be a subset of the $W$ -favoured outlooks, and so already in $W *$ . ⮭
Thanks to an anonymous referee for pressing this worry. ⮭
$a$ would be $W$ -favoured, but not $W *$ -favoured. This potential discrepancy is a feature of the account: we can use the $W *$ -favoured outlooks to make sense of higher-orders of determinacy: e.g., it is determinately determinately correct to believe that $p$ iff $[p]$ is favoured by $W * *$ (where $W * *$ is the union of the improvement* sets of the $W *$ -favoured outlooks); and it is determinately determinately determinately correct to believe that $p$ iff $[p]$ is favoured by $W * * *$ ; and so on up the hierarchy. ⮭
Similarly, if indeterminacy really seems beyond the pale, we should doubt the reasonableness of all the outlooks. ⮭
If fundamental disagreement suffices for indeterminacy and there is a proper attitude to take towards indeterminate matters—e.g., suspension of judgement—then fundamental disagreement is unlikely to be widespread: if we fundamentally disagree, then we can both improve by suspending judgement; but if we both suspend judgement, then we no longer disagree; so the disagreement wasn’t fundamental after all. (Something similar goes given conciliationism about peer disagreement—see fn. 35.) Nonetheless, indeterminacy remains just as widespread. ⮭
See also Lenman (2014: 241) and Rowland (2017). Rowland argues that widespread fundamental moral disagreement would entail that our understanding of morality is “fatally flawed”. ⮭
Another salient option is give up absolutism in favour of relativism. This is open to the expressivist, who can relativise normative correctness to (sets of) improvement* sets. I work in the absolutist framework for simplicity (see fn. 33). ⮭
An identical dialectic plays out with regards to unstable-points, which also suffice (if reasonable) for indeterminacy on my account: (i) it’s not obvious that there are widespread unstable-points, and (ii) if unstable-points are widespread the accompanying proliferation of indeterminacy does not make matters worse. On (i): let a flip-flopping series be an infinite series of distinct outlooks $x 1, x 2$ , etc., each accessible from the last, such that $[p] ∈ x 1$ , $[p] ∉ x 2$ , $[p] ∈ x 3$ , $[p] ∉ x 4$ , and so on indefinitely; and let an improvement loop be a pair of outlooks, $x 1$ and $x 2$ , each accessible from the other, such that $[p] ∈ x 1$ and $[p] ∉ x 2$ . For $x$ to be an unstable-point for $[p]$ requires, not just that $x$ is a member of a flip-flopping series or improvement loop, but that every outlook accessible from $x$ is so too. This is a demanding constraint for an improvement* set to satisfy. On (ii): if $x$ is an unstable-point for $[p]$ and there is a determinate fact of the matter, then $x$ cannot settle on the determinately correct answer through successful normative inquiry. Again, this sceptical diagnosis does not seem preferable to saying the matter is indeterminate.
The same goes vis-à-vis stable-points for both $[p]$ and $[¬ p]$ , if we say this suffices for indeterminacy (fn. 27). (i) If $x$ values consistency, then eliminating a contradiction counts as an improvement by $x$ ’s lights. So, if $x$ is a stable-point for both $[p]$ and $[¬ p]$ , either $x$ does not value consistency (and so is plausibly unreasonable)—or else all possible attempts to improve by eliminating the contradiction are systematically outweighed by compensating deteriorations by the lights of the other higher-order norms $x$ endorses. (ii) If there is a determinate fact of the matter, then self-improvement cannot dislodge a determinately incorrect judgement. This diagnosis does not seem preferable to saying the matter is indeterminate. ⮭
Nor this account of the correctness conditions of a desire-like attitude for an account of the content of a representational state. ⮭

References

Ayer, Alfred. J. (1936). Language, Truth and Logic. Victor Gollancz.

Baker, Derek and Jack Woods (2015). How Expressivists Can and Should Explain Inconsistency. Ethics, 125(2), 391–424. https://doi.org/10.1086/678371 https://doi.org/10.1086/678371

Beddor, Bob (2020). Fallibility for Expressivists. Australasian Journal of Philosophy, 98(4), 763–77. https://doi.org/10.1080/00048402.2019.1699586 https://doi.org/10.1080/00048402.2019.1699586

Bex-Priestley, Graham (2018). Error and the Limits of Quasi-Realism. Ethical Theory and Moral Practice, 21(5), 1051–63. https://doi.org/10.1007/s10677-018-9945-z https://doi.org/10.1007/s10677-018-9945-z

Blackburn, Simon (1971). Moral Realism. In John Casey (Ed.), Morality and Moral Reasoning (101–24). Methuen.

Blackburn, Simon (1984). Spreading the Word: Groundings in the Philosophy of Language. Clarendon Press.

Blackburn, Simon (1992). Morality and Thick Concepts: Through Thick and Thin. Proceedings of the Aristotelian Society Supplementary Volume 66(1), 285–99. https://doi.org/10.1093/aristoteliansupp/66.1.267 https://doi.org/10.1093/aristoteliansupp/66.1.267

Blackburn, Simon (1993). Essays in Quasi-Realism. Oxford University Press.

Blackburn, Simon (1996). Securing the Nots: Moral Epistemology for the Quasi-Realist. In Walter Sinnott-Armstrong and Mark Timmons (Eds.), Moral Knowledge?: New Readings in Moral Epistemology (82–100). Oxford University Press.

Blackburn, Simon (1998). Ruling Passions: A Theory of Practical Reasoning. Oxford University Press.

Blackburn, Simon (2009). Truth and A Priori Possibility: Egan’s Charge against Quasi-Realism. Australasian Journal of Philosophy, 87(2), 201–13. https://doi.org/10.1080/00048400802362182 https://doi.org/10.1080/00048400802362182

Blackburn, Simon (2013). Disentangling Disentangling. In Simon Kirchin (Ed.), Thick Concepts (121–35). Oxford University Press.

Chang, Ruth (2002). The Possibility of Parity. Ethics, 112(4), 659–88. https://doi.org/10.1086/339673 https://doi.org/10.1086/339673

Dreier, James (2004). Meta-Ethics and the Problem of Creeping Minimalism. Philosophical Perspectives, 18(1), 23–44. https://doi.org/10.1111/j.1520-8583.2004.00019.x https://doi.org/10.1111/j.1520-8583.2004.00019.x

Dunaway, Billy (2010). Minimalist Semantics in Meta-Ethical Expressivism. Philosophical Studies, 151(3), 351–71. https://doi.org/10.1007/s11098-009-9438-y https://doi.org/10.1007/s11098-009-9438-y

Egan, Andy (2007). Quasi-Realism and Fundamental Moral Error. Australasian Journal of Philosophy, 85(2), 205–19. https://doi.org/10.1080/00048400701342988 https://doi.org/10.1080/00048400701342988

Field, Hartry (1994). Disquotational Truth and Factually Defective Discourse. Philosophical Review, 103(3), 405–52. https://doi.org/10.2307/2185788 https://doi.org/10.2307/2185788

Gibbard, Allan (1990). Wise Choices, Apt Feelings: A Theory of Normative Judgement. Oxford University Press.

Gibbard, Allan (2003). Thinking How to Live. Harvard University Press.

Horgan, Terrence and Mark Timmons (2015). Modest Quasi-Realism and the Problem of Deep Moral Error. In Robert Johnson and Michael Smith (Eds.), Passions and Projections: Themes from the Philosophy of Simon Blackburn (190–209). Oxford University Press.

Horwich, Paul (1998). Truth (2nd ed.). Oxford University Press.

Köhler, Sebastian (2015). What Is the Problem with Fundamental Moral Error? Australasian Journal of Philosophy, 93(1), 161–65. https://doi.org/10.1080/00048402.2014.928736 https://doi.org/10.1080/00048402.2014.928736

Lam, Garrett (2020). Making Quasi-Realists Admit of Fundamental Moral Fallibility. Australasian Journal of Philosophy, 98(2), 294–303. https://doi.org/10.1080/00048402.2019.1611892 https://doi.org/10.1080/00048402.2019.1611892

Lenman, James (2014). Gibbardian Humility: Moral Fallibility and Moral Smugness. Journal of Value Inquiry, 48(2), 235–45. https://doi.org/10.1007/s10790-014-9420-6 https://doi.org/10.1007/s10790-014-9420-6

Peirce, Charles. S. (1878). How to Make Our Ideas Clear. Popular Science Monthly, 12(1), 286–302.

Putnam, Hilary (1981). Reason, Truth and History. Cambridge University Press.

Ridge, Michael (2014). Impassioned Belief. Oxford University Press.

Ridge, Michael (2015). I Might Be Fundamentally Mistaken. Journal of Ethics and Social Philosophy, 9(3), 1–22. https://doi.org/10.26556/jesp.v9i3.92 https://doi.org/10.26556/jesp.v9i3.92

Rowland, Richard (2017). The Significance of Significant Fundamental Moral Disagreement. Noûs, 51(4), 802–31. https://doi.org/10.1111/nous.12170 https://doi.org/10.1111/nous.12170

Schroeder, Mark (2013). Two Roles for Propositions: Cause for Divorce? Noûs, 47(3), 409–30. https://doi.org/10.1111/j.1468-0068.2011.00833.x https://doi.org/10.1111/j.1468-0068.2011.00833.x

Stevenson, Charles (1944). Ethics and Language. Yale University Press.

Väyrynen, Pekka (2019). Thick Ethical Concepts. In Edward Zalta (Ed.), The Stanford Encyclopedia of Philosophy (Summer 2019 ed). Retrieved from https://plato.stanford.edu/archives/sum2019/entries/thick-ethical-concepts/https://plato.stanford.edu/archives/sum2019/entries/thick-ethical-concepts/

Williams, J. Robert G. (2014). Decision-Making Under Indeterminacy. Philosophers’ Imprint, 14(4), 1–34.

Williams, J. Robert G. (2017). Indeterminate Oughts. Ethics, 127(3), 645–73. https://doi.org/10.1086/690071 https://doi.org/10.1086/690071