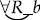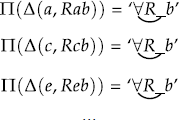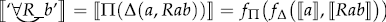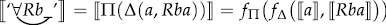A central achievement of early analytic philosophy was the development of a formal language capable of representing the logic of the quantifiers. There are two dominant approaches to quantification: the Fregean and the Tarskian. Fregeans generalize the semantics of quantification from the semantics of atomic sentences and sentences composed with truth-functional connectives. This approach is widely held to be more philosophically satisfactory because the Fregean allegedly preserves the standard referential semantics for names and retains truth (or propositional content) as the central notion in a compositional semantic theory. By way of contrast, the Tarskian alternative, though mathematically elegant, abandons either compositionality or the centrality of truth and reference in semantic theory. For example, in comparing the Fregean and Tarskian approaches, Evans says:
. . . [T]he Fregean theory with its direct recursion on truth is very much simpler and smoother than the Tarskian alternative, whose mechanism of infinite sequences differing in at most this or that place is dispensed with. But its interest does not stem from this, but rather from examina-tion at a more philosophical level. It seems to me that serious exception can be taken to the Tarskian theory on the ground that it loses sight of, or takes no account of, the centrality of sentences (and of truth) in the theory of meaning. (Evans 1977: 476)
The central fault of the Tarskian approach is claimed to be its incorporation of variables to construct open sentences.1 These open sentences are not true or false absolutely and so displace truth as the central notion in the theory of meaning.
We argue that the Fregean approach faces the same choice: abandon compositionality or abandon the centrality of truth and reference to semantic theory. Indeed, we argue that developing a fully compositional semantics in the tradition of Frege leads to a typographic variant of the most radical of Tarskian views: variabilism, the view that names should be modeled as Tarskian variables. We conclude with the consequences of this result for Frege’s distinction between sense and reference.
1. The Base Language
Can Fregeans offer a theory of quantification that naturally extends the semantics of the non-quantified portion of the language? In particular, can they offer a semantic theory that takes reference and truth as the central notions of the semantic theory? In this section, we describe the syntax and semantics for the non-quantified portion of the language that is common between Frege and Tarski. In the next section, we examine how Tarski modifies this picture—abandoning either the centrality of reference and truth or compositionality—in his effort to offer a semantics for quantification. We then examine Fregean attempts to offer a semantics for quantification which preserves the semantics assigned to the non-quantified portion of the language.
Frege and Tarski each offer a truth-theory for the sentences of a language. Tarski’s theory entails a sentence of the form is true if and only if , for each sentence S of the language (Tarski 1935/1956a). Tarski himself thought that a theory yielding entailments of this kind would provide a satisfactory account of truth. In contemporary semantics—in both the Davidsionian (Larson & Segal 1995) and Montagovian (Heim & Kratzer 1998) traditions—a theory of this kind is said to act as a theory of meaning for the language. A Fregean semantic theory characterizes a function, , which assigns a denotation (Bedeutung) to every expression of the language. Frege’s truth theory specifies when a sentence of the language denotes the True (Frege 1893/2013). The truth conditions of a sentence depend on the denotations of the expressions from which it is syntactically derived.
A semantic theory requires a structural description of every sentence in the language. A language contains a set of basic expressions. A derived expression— including a sentence—results from the application of a syntactic construction rule to more basic expressions. For example, a conjunction such as (3) below is syntactically derived by applying a construction rule to its two conjuncts (1) and (2), which in turn syntactically derive from applying the predication construction rule to the names and predicates that make them up.
Annabel smiles.
Hazel waves.
Annabel smiles and Hazel waves.
How we describe these syntactic construction rules depends on how we think of the complex expressions. For example, a complex expression might be treated as a string of basic expressions, where the conjunction rule puts the word ‘and’ between the two sentences it applies to and the predication rule juxtaposes a name and a predicate. Or a complex expression might instead be treated as a tree, where the rules map expressions to tree structures consisting of the input expressions. There may also be rules (“transformation rules”) that manipulate strings or trees in more complex ways, for instance by deleting or replacing all occurrences of a certain expression (see Chomsky 1957). If complex expressions are treated as something besides trees or strings of basic expressions, say Gödel numbers, then the various syntactic construction rules differ, for example, they may be arithmetic operations. As we will see, these more complicated syntactic construction rules appear in Frege’s syntax for quantification.
The structural description of the quantifier free portion of the language (which we will call the base language) can be generated by an initial lexicon and three syntactic construction rules. The lexicon includes terms and predicates.2 Terms include denumerably many lower case letters for names from the beginning of the alphabet . The predicates, with adicity marked by the superscript n, include denumerably many upper case letters . The syntactic construction rules are as follows.
: Takes an -place predicate and terms, , and yields a sentence. We represent this sentence as .
: Takes a sentence and yields a sentence. We represent this sentence as .
: Takes a pair of sentences and and yields a sentence. We represent this sentence as .
Nothing else is a sentence of the language. Note that instances of , , or are metalanguage descriptions of object language expressions rather than object language expressions themselves. In particular, they describe a formula as the result of applying the operations of predication, negation, and conjunction to more basic expressions.3
The principle of compositionality relates the semantic contribution of a derived expression to the semantic contribution of the simpler expressions from which it is derived. Namely, if two expressions are derived by applying the same syntactic formation rule to a sequence of co-denoting expressions, then the derived expressions themselves co-denote. The compositionality principle can be formally stated as follows, where is a syntactic rule for deriving a complex expression from more basic expressions.
compositionality: If
This is the standard notion of semantic composition used in linguistic semantics in the tradition of Montague (cf. Pagin & Westerståhl 2010).4 But compositionality has its roots in Frege. Because of its historical roots, it has even been referred to as “Frege’s Principle” (Carnap 1947: 121; Cresswell 1973: 76).5
The truth conditions for the base language can be specified in a way that respects compositionality. The denotation of a term is its referent, . The denotation of an -predicate is its extension , which is a set of -tuples. The semantic values of complex sentences can be specified as follows.
Predication Rule:
Negation Rule:
Conjunction Rule:
Thus, (1) ‘Annabel smiles’ is true just in case the referent of ‘Annabel’ is in the extension of ‘smiles’ and (2) ‘Hazel waves’ is true just in case the referent of ‘Hazel’ is in the extension of ‘waves’. The conjunction (3) is true if and only if ‘Annabel smiles’ is true and ‘Hazel waves’ is true.
In this semantics, each sentence is assigned a truth-value as its denotation. So, truth plays a central role in theory of meaning, as Evans says above.
truth centrality: The denotation of a sentence is a possible argument for a truth function. Therefore, the denotation of a sentence is its truth-value.
The contribution a sentence makes to the truth conditions of sentences that contain it is just its truth-value.
The contribution of a term is also just its referent. Two terms that co-refer make the same contribution to the truth conditions of sentences that contain them. In this respect, the notion of reference—the link between a word and what it picks out in the world—is also central to the theory of meaning.6
reference centrality: The denotation of a term is fit to be in the extension of a predicate. Therefore, the denotation of a term is an object, its referent.
Thus, the semantics for this base language is compositional and is fundamentally constrained by the assignments of truth and reference to sentences and terms.
2. The Tarskian Theory
The challenge is to compositionally extend the semantics of the base language to cover quantification while preserving truth and reference centrality. We now examine Tarski’s semantics for quantification in order to develop the complaint that it is either non-compositional or that it abandons truth and reference centrality.7
To account for quantification, Tarski must first extend the syntax of the language. Consider a sentence such as ‘everything smiles and waves’. The sentence is constructed by applying a syntactic rule connecting the quantifier ‘everything’ to ‘smiles and waves’. Because Tarski (1935/1956a) treats ‘and’ as a sentential connective, it occurs between two expressions of the same syntactic type as sentences in his formal correlate of ‘smiles and waves’. So Tarski needs to construct sentences in his formal language that can be conjoined. Tarski extends the lexicon to include explicit variables . These variables are terms insofar as they occupy the same syntactic positions as proper names. Thus, ‘ smiles’ and ‘ waves’ are both of the same syntactic type as sentences. We call everything of this type a sentence and refer to an expression of sentence type containing free variables as an open sentence.
Open sentences play a key role in constructing quantified sentences in Tarski’s language. The open sentences ‘ smiles’ and ‘ waves’ may be conjoined to yield the open sentence ‘ smiles and waves’. A quantified sentence is constructed from a variable and an open sentence by the following construction rule.
-
∀
Takes a variable and a sentence and yields a sentence. We represent this sentence as .
Thus, ‘ smiles and waves’ may be fed into the quantification rule to yield sentence (4).
(4) is such that smiles and waves.
In (4), the universal quantifier ‘ is such that’ functions as a sentential connective. Sentence (4), or really , is Tarski’s formal correlate of ‘Everything smiles and waves’.
Appealing to these syntactic descriptions, Tarskians have offered two sorts of recursive theory for characterizing the truth conditions for quantified sentences in terms of the denotations of the expressions they derive from. One sort of theory—developed in Tarski (1935/1956a)—can be construed as preserving truth and reference centrality but violating compositionality, and this has been the source of the persistent claim that Tarski’s semantic theory is not compositional (Salmon 2006a; Partee 2013; Soames 2010: 64 fn. 9). The other sort of theory— also developed by Tarski and his students8—is compositional, but abandons the centrality of both truth and reference, leading to complaints of the sort raised by Evans. We examine each proposal in turn.9
2.1. Assignment-Relative Semantics
The problem for the Tarskian theory arises from its commitment to explicit variables and open sentences in the syntax. Although variables and proper names are of the same syntactic type, terms, their semantic contribution is very different. Whereas a name refers to a particular object, a variable picks out different objects relative to different assignments. For any assignment , let be a function that takes an expression to its denotation on that assignment. The denotation of a constant is the same object, its referent, for any assignment. The value of a variable depends on the assignment .
Terms:
.
.
Similarly, an open sentence such as ‘ smiles’ is not true or false absolutely. The open sentence is satisfied by (or true relative to) some assignments and unsatisfied by (or false relative to) others. For example, ‘ smiles’ is only satisfied by those assignment functions that assign the variable to a smiling individual. Thus, satisfaction by (or truth relative to) an assignment for atomic predication is defined as follows (where is the extension of the predicate ):
Predication Rule:
The truth conditions of sentences constructed using truth-functional connectives are also as they were in the base language.
Negation Rule:
Conjunction Rule:
So far, the semantic theory resembles exactly the semantic theory for the base language. Moreover, the clauses are compositional since the semantic value of an expression at an assignment is a function of its constituents’ semantic values at that same assignment.
However, compositionality fails when the language takes quantifiers into account. The denotation of a quantified claim at an assignment is not a function of the denotations of the variable and the sentence at . The denotation of at depends on the denotations of and the sentence at other assignments. If is an assignment function and is a variable, then let be the assignment that differs from assignment at most in that it assigns o to . A universally quantified sentence is satisfied by an assignment if for every object , satisfies .
Quantification Rule:
A sentence is true (simpliciter) if it is satisfied by every assignment. Thus, (4) is true if and only if the embedded open sentence ‘ smiles and waves’ is satisfied by every assignment function.
On this semantics, assigns each expression to its denotation. The function satisfies truth and reference centrality. As a consequence, it violates compositonality. To see this, consider quantified formulae that are constructed by application of the same syntactic rule, such as and :
Assume that and co-denote relative to assignment . By compositionality, it follows that . Again by compositionality, it follows that .10 But these formulae aren’t equivalent: everything might stand in a relation to object without standing in to everything. This shows that the function does not compositionally assign expressions to their denotations. This argument is fully general. Any denotation function that preserves truth and reference centrality for this language and yields results in failures of compositionality
compositionality is a core methodological constraint on semantic theorizing (see Partee 1984 and Dever 1999). Abandoning it would require revisiting every choice that it has previously motivated. It also has empirical content, explaining how a language user can understand an infinity of complex expressions by understanding a finite base of simple expressions and rules for forming complex expressions out of simpler expressions (see, e.g., Heim & Kratzer 1998).
This failure of compositionality does not exclusively rely on truth and reference centrality, which one may take to involve overly narrow conceptions of the semantic contributions of a sentence and term. It extends, for example, to those who think that the primary semantic function of a sentence is to express a content, a possible worlds intension or a structured Russellian or Fregean proposition. The problem would arise for any view on which two open sentences have the same denotation (relative to an assignment) but differ by the substitution of variables or by the substitution of a variable for a singular term.11 Retaining compositionality would require abandoning this assumption. But many have worried that such a view “demotes” propositions to “secondary importance in semantics” because the contribution that a sentence makes to the truth-conditons of a sentence that contains it is not the proposition it expresses (King 2003: 200).12
2.2. Assignment-Sensitive Semantics
As developed above, the Tarskian semantics is not compositional. However, a compositional theory can be provided for the Tarskian account with a shift of perspective. Instead of construing denotations as assignment relative, make denotations assignment sensitive. In this way the denotation of a term is something other than its referent (at an assignment), namely a function from an assignment to an object. In particular a variable denotes the function from assignment to whatever assigns to . The denotation of a name is a constant function from assignments to objects, e.g., for some it may be that . The denotation of an -place predicate is an -tuple of objects. With those assumptions in place, the semantic clause for quantification can be given as follows.
A semantic theory of this kind is compositional.13 But it obviously abandons the doctrines that the denotation of a term is an object and the denotation of a sentence is a truth-value. In this way the Tarskian has been shown to face the dilemma of having to either (i) abandon compositionality or (ii) abandon truth and reference centrality.
Therefore, in order to preserve compositionality, the Tarskian must make rather severe adjustments to the semantic clauses for the base language. For example, in the base semantics, one might be tempted to view proper names as making word-world connections. The job of a proper name is to stand for its referent. A sentence containing a proper name says something about this referent. The function of a variable, on the other hand, is partly given by its role in bound constructions. A bound variable does not contribute an object which the remainder of the sentence says something about. Rather, it interacts in a distinctive way with antecedent quantifiers.
In the compositional version of the Tarskian semantics, neither variables nor proper names denote their referents. Rather, they denote functions from assignments to individuals. The distinction between proper names and variables can be preserved by holding that proper names denote constant functions but the function denoted by a variable may have different values for different arguments.14 Thus, variables may be non-vacuously bound whereas for proper names–even if they could be bound—the binding would be vacuous.
However, some hold that even this distinction is artificial from the perspective of compositional semantics. According to variabilism about names, the denotation of a proper name—like the denotation of a variable—may yield different values for different assignment functions. Indeed, most variabilists would argue that even proper names may be bound in natural language and that it would be appropriate to provide a regimentation that allows for this sort of binding. They therefore propose that proper names in natural language should be regimented using Tarskian variables.15
3. The Fregean Alternatives
The failure of compositionality or of truth and reference centrality endemic to the Tarskian semantics might seem to originate from the appeal to variables as genuine syntactic units. The Fregean approach has been held to evade these worries. Fregeans insist that the only “variables” that appear in their formalisms are mere marks of punctuation or are even completely eliminable. In avoiding variables and open sentences, the Fregean claims to offer a compositional semantic theory centered on truth and reference. In addition to Evans (1977), theorists such as Dummett (1973), Cresswell (1973), Partee (2013), Heck (2012), Smith (2017), Wehmeier (2018; 2021), Potter (2020), and Button and Walsh (2018) have each suggested that some aspect of the Fregean account frees it from the difficulties faced by the Tarskian.
Frege regimented quantified sentences of natural language into his formal language, the Begriffsschrift, which contained explicit construction rules for syntactically deriving sentences including quantified formulae. The syntactic formation and semantic evaluation rules for this language are most clearly presented in Basic Laws §30 (Frege 1893/2013). These rules look very different from the contemporary Tarskian approach. Dummett illustrates the syntactic derivation of a Fregean quantified sentence using the natural language sentence ‘everybody envies somebody’ as follows.16 We add labels A, B, and C to the steps in order to aid exposition.
[A] we begin with a sentence such as ‘Peter envies John’. [B] From this we form the one-place predicate ‘Peter envies ’ by removing the proper name ‘John’—the Greek letter ‘ ’ here serving merely to indicate where the gap occurs that is left by the removal of the proper name. [C] This predicate can then be combined with the sign of generality ‘somebody’ to yield the sentence ‘Peter envies somebody’. The resulting sentences may now be subjected to the same process: by removing the proper name ‘Peter’, we obtain the predicate ‘ envies somebody’, and this may then be combined with the sign of generality ‘everybody’ to yield the sentence ‘Everybody envies somebody’. (Dummett 1973: 11)
There are three features of the Fregean syntax for predicate logic that—it might be hoped—aid in avoiding the dilemma.
F1. Quantifiers are predicates of predicates. The Tarskian syntax treats a quantified formula as derived from applying the construction rule for the quantifier to the variable and the formula . The Fregean derives a quantified formula by applying the construction rule for the quantifier to a predicate ( ). (Step [C] above.)
F2. Quantified formulae are derived from names and closed sentences. The Tarskian syntax treats quantified sentences (or complex predicates) as ultimately constructed from open sentences which contain variables. The Fregean syntax first constructs a closed sentence and a name. It then constructs the quantified sentence (or complex predicate) by the application of a syntactic rule to the name and the closed sentence. (Step [A] to [B] above.)
F3. Alphabetic variants are identical. The standard Tarskian syntax does not identify alphabetic variants. Thus the sentence is distinct from the sentence and the complex predicate is distinct from the complex predicate . In contrast, the Fregean syntactically identifies the complex predicate that results from removing from with the complex predicate that results from removing from . The Fregean identifies this complex predicate as an expression containing a “gap”: ‘ ’. Or using Frege’s gapmarkers, ‘ ’. (Step [B] above.) This type of approach has been extended by more recent proponents who appeal to Quine-Bourbaki diagrams in order to render a quantified formulae such as as follows (adapted from Kaplan 1986: 244):
In the remainder of this section we examine each feature in detail, spelling out why it has been held to be advantageous. We argue that these contrasts are individually and collectively insufficient to exculpate Fregean approaches from the charges against the Tarskian approach. We examine proposals that in one way or another take up a Fregean approach to quantification. Our contention is that when Fregean approaches are spelled out precisely they end up having the same alleged vices as the Tarskian account. They either end up violating the compositionality principle or they demote truth and reference from their central role in the semantic theory. Moreover, we argue that compositional versions of the Fregean approach are variabilist in the sense discussed above: a single category of expression both regiments proper names and plays the role of Tarskian variables in the derivation and semantic evaluation of quantified sentences.
3.1. Quantifiers as Predicates of Predicates
On standard presentations, the Tarskian quantifier, ‘ ’, serves a double-duty: it both binds variables in its scope and generalizes. The truth-value of a quantified formula relative to an assignment depends on the truth-value of the embedded formula relative to assignments that differ from only in their interpretation of . The quantified formula is true if and only if the embedded formula is true on all assignments. The contribution of the quantifier to the truth conditions of a sentence that contains it is obscured by serving these two roles.
According to Fregean approaches, a quantifier has a single semantic role of generalizing a predicate (feature F1). A sentence that results from applying the universal quantifier ‘everything’ to a predicate is true if and only if the predicate is true of every object and a sentence that results from applying the existential quantifier ‘something’ to a predicate is true if and only if the predicate is true of some object.
(5) Everything smiles.
(6) Something waves.
Thus, (5) is true if everything smiles and (6) is true if something waves.
There are two reasons one might view the Fregean approach as preserving compositionality in contrast to the Tarskian. The first is that the Fregean explicitly assigns a meaning to the quantifier symbol ‘
’. This position is articulated by Partee (2013: 120–21), who says that Frege’s development of predicate logic was carried out “more compositionally” than Tarski’s, where “the quantifier symbols
and
are not themselves given a semantic interpretation”. Indeed, Frege provides a denotation for his quantifier symbol ‘ ’. Or, rather, Frege provides the same denotation for his many synonymous quantifier symbols, each indexed by a different Gothic letter. (Looking ahead to feature F3, we will ignore this feature of Frege’s syntax.)17 However, as we have seen, nothing prevents the Tarskian from assigning a meaning to the quantifier expressions as well.
’. Or, rather, Frege provides the same denotation for his many synonymous quantifier symbols, each indexed by a different Gothic letter. (Looking ahead to feature F3, we will ignore this feature of Frege’s syntax.)17 However, as we have seen, nothing prevents the Tarskian from assigning a meaning to the quantifier expressions as well.
Therefore, we turn to the second potential advantage: variables are not immediate constituents of quantified formulae. Along these lines, Cresswell (1973: 80–87) cites the familiar difficulty in accounting for the semantic difference between and , if and happen to share their referent. Cresswell insists that by treating the quantifier as attaching to a complex predicate which is constructed by abstraction, one can then treat the quantifiers as straightforward predicates of predicates, and thereby avoid the problems that plague the standard syntax.
Yet there remains a major lacuna in the semantics. Not every quantified statement results from applying a quantifier phrase to a simple predicate.18 Consider (7).
(7) Something smiles and waves.
This sentence results from applying the quantifier ‘Something’ to the predicate ‘smiles and waves’. But this latter predicate cannot be a simple predicate. In particular, we want to be able to explain the fact that (7) entails (6) and (8).
(6) Something waves.
(8) Something smiles.
To deliver this explanation, the predicate ‘smiles and waves’ must be syntactically derived from the simpler predicates ‘smiles’ and ‘waves’. The central challenge to the Fregean approach, then, is to provide a compositional account of the formation and semantic evaluation rules for these syntactically derived predicates.
Contemporary semanticists follow Frege by constructing quantified formulae using two formation rules: one derives a complex predicate from a variable and an open sentence and the other attaches the quantifier to the complex predicate.19
: Takes a variable and a sentence and yields a monadic predicate. We represent this predicate as .
: Takes a monadic predicate and yields a sentence. We represent this sentence as .
The first step corresponds to the binding work (predicate abstraction, or “lambda binding”), while the second corresponds to the quantificational work. Visually, one can compare the standard Tarskian syntax on the left with this Fregean departure on the right:
A quantified formula is true on this approach if the embedded predicate is true of all objects.
The challenge for the Fregean in implementing this proposal is to semantically characterize complex predicates in terms of the expressions from which they derive. In contemporary formal semantics, this problem is relocated to the semantics of abstraction. Consider predicates that are constructed by applying the same syntactic rule, such as the following:
If the terms and co-denote, then , and so it follows—by compositionality—that . But, of course, these predicate abstracts should denote distinct properties, the properties of being an that stands in to and being an that stands in to, respectively. So separating quantification from abstraction is no advance in terms of violations of compositionality. Abstraction does not save compositionality—it instead locates precisely where it fails (given the Fregean assumptions).20
We can, however, provide a compositional semantics for this syntax by again making anti-Fregean assumptions about denotation. We replace the semantic clause for quantification with the following two clauses:21
Abstraction Rule:
Quantification Rule:
While an approach that employs abstraction may be advantageous in terms of providing an explicit meaning to the quantifier, the approach described here clearly does not avoid the dilemma because it relies on the assumption that the denotation of a variable is a function from assignments to objects and the denotation of a sentence is a function from assignments to truth-values.
3.2. Recursion on Names and Closed Sentences
An apparently distinctive feature of Fregean syntax is its avoidance of “open” sentences and variables. Whereas the Tarskian syntax constructs quantified sentences from open sentences which contain variables, the Fregean syntax first constructs a closed sentence, then constructs a predicate by a process of name removal, and finally combines the resulting predicate with a quantifier. This is feature F2 of Frege’s program. We argue that direct recursion on names and closed formulae in this manner forces the same uncomfortable choice faced by Tarski.
Syntactically, Fregean approaches defined by F2 differ from the Tarskian approach in two respects: (i) the language includes only terms drawn from the beginning of the Latin alphabet rather than additionally containing terms from the end of the alphabet and (ii) the abstraction rule is replaced with the following rule:22
: Takes a name and a sentence and yields a monadic predicate. We represent this predicate as .
Rule differs from rule only by appealing to letters at the beginning rather than end of the alphabet. And, of course, merely avoiding the use of lower case letters from the end of the alphabet cannot in itself be advance on the Tarskian approach. Nothing prohibits using the beginning of the alphabet for variables. This choice of alphabetic location is arbitrary.
But the Fregean doesn’t just avoid use of certain parts of the alphabet, they use the same set of terms—the names—to regiment ordinary proper names and to derive complex predicates or quantified formulae. In contrast, a textbook Tarskian system (e.g., Kalish & Montague 1964) has two syntactic species within a broader genus of terms—names and variables—and the category of names regiments proper names of ordinary language, while the category of variables are used to derive quantified formulae. For the Fregean, all terms are names, but names enter into the construction rules in two different ways.
The use of a unified category of terms rather than a bifurcated category does not interestingly differentiate the Fregean from the Tarskian approach. In fact, using two categories of terms is not essential to the the Tarskian approach—the languages defined in, e.g., Tarski (1935/1956a) and Tarski and Vaught (1957) didn’t actually have a category of names in addition to the variables. For us, the question of whether an expression is a variable is tantamount to the question of whether it can play the role of variables in a quantified sentence. That is, expressions that can be non-trivially bound by operators are variables. The fact that an expression may also perform a different function while not bound is irrelevant.
Our position regarding Frege’s syntax agrees with Carnap (1934/1959: §54), when he considers the similar position that quantified sentences might be constructed using constants rather than variables. (He attributes this possibility to Quine.) Thus, rather than ‘ ’, one might have ‘ ’ or ‘ ’, where ‘ ’ and ‘ ’ are numerical constants. Carnap argues that even if this language lacks free variables (because he treats open sentences as having universal force), the proper names are nonetheless variable-expressions, since they play the relevant role in the construction of quantified formulae.
F2 is a form of variabilism, names and variables constitute a unified semantic category. It differs from more recent forms of variablism only by using letters from the beginning of the alphabet rather than the end to regiment names and variables.23 Both contemporary and Fregean approaches use the same sort of expression to regiment (referential) proper names and in the derivation of complex predicates or quantified sentences. Thus, there is no interesting syntactic difference between the Fregean who forms complex predicates by applying a construction rule to names and closed sentences and the Tarskian who does so by applying a construction rule to variables and open sentences. The syntactic difference lies only in the alphabetic location of the “variables”.
If Fregeans want to offer a genuine alternative to the Tarskian approach, they must offer a substantively different semantics for abstraction from that offered by the Tarskian. In particular, Fregeans must offer a semantics that evades the dilemma. But the only compositional implementation of Frege’s idea gives up truth and reference centrality.
Suppose that the Fregean wishes to maintain truth and reference centrality. Consider predicates that are constructed by applying the same syntactic rule, such as abstracting the name from and :
If the names and refer to the same object, then, by compositionality, it follows that , and then again by compositionality it follows that . But, of course, these predicate abstracts should denote distinct properties, the properties of being an that stands in to and being an that stands in to, respectively. So, compositionality fails for the Fregean approach.24 The appeal to letters from the beginning rather than the end of the alphabet has in no way changed the underlying semantic picture.
Dummett (1973: 16–18) argued that there was “no real contrast” between the Tarskian account of the formation of quantified sentences deploying variables and Frege’s account that deploys names. Dummett’s reason is that
. . . a free variable is treated exactly as if it were a proper name at every stage in the step-by-step construction of a given sentence up to that at which a quantifier is to be prefixed which will bind that variable. (1973: 17)
To a certain extent, we agree with Dummett here. In both approaches, a quantified sentence is first formed by applying the predication rule to a predicate and some terms. The relevant complex predicate is then constructed by applying an abstraction rule, before applying the quantification rule. Thus, the Tarskian and Fregean syntactic derivations are structurally isomorphic.
Tarskian Derivation:
Fregean Derivation:
Dummett (1981: 284–86), however, went on to argue that the Tarskian semantics gives up the advantages of the Fregean approach, namely, that the denotation of a complex sentence can be understood in terms of the truth conditions of the closed atomic sentences from which it is derived. However, we think the equivalence goes the other way. Given that the complex predicate is derived from the name and the sentence , the denotation of the name must include more than its referent and the denotation of the sentence must include more than its truth-value (or truth-conditions). Otherwise, will be identical to , should and happen to have the same denotation.
3.3. Identification of Alphabetic Variants
We now turn to the third, and final, element of Frege’s approach to quantification: F3. As Dummett remarked, Frege’s syntactic rule removes or excludes a name such as ‘Annabel’ from a sentence such as ‘Annabel waves’, leaving a gap or mark of incompleteness . The resulting predicate abstract can be written as ‘ waves’. Removing a different name, ‘Hazel’, from a corresponding sentence, ‘Hazel waves’, results in the same predicate abstract, ‘ waves’. Generalizing, if predicate abstract results from the application of the removal operation to a name and a sentence and results from the application of the removal operation to a name and a sentence differing from φα only by the total proper substitution of for , then and are syntactically identical. On this view, alphabetically-variant complex predicates are strictly and literally identical:
So, contrary to a more standard syntax (§3.1), there are multiple ways to syntactically derive one and the same complex predicate. The metaphor often used here is “removal” of a name (or as Frege says “einen Eigennamen ausschließen”) from the sentence—the names that contribute to their derivation do not show up in the finished product. This is why the resulting predicate abstract ‘ ’ has a gap or mark of incompleteness.
The name doesn’t occur in the resulting predicate abstract ‘ ’, but it does figure in a syntactic derivation of the predicate abstract.
For many formal languages one can read a syntactic derivation off of the part-whole structure of a derived expression. There is therefore a temptation to conflate the notions of parthood and syntactic derivation. However, Frege’s rule for constructing complex predicates is a transformation rule (in the sense of Chomsky 1957) requiring us to delete all embedded occurrences of a name from the output string. One may specify this string as result of applying the construction rule to and . Or, one may specify this string intrinsically as a certain sequence of marks (e.g., ‘ ’, ‘ ’, ‘ ’ or ‘ ’) or as a Gödel number. But the latter is an issue for the science of calligraphy not logic.25
In Frege’s own semantics, there remains a hint of “variables” in the typography of quantified formulae because these result from saturating a dispersed quantifier sign which contains a Fraktur letter ‘ ’ with a complex predicate such as ‘
’, yielding ‘
’ with a complex predicate such as ‘
’, yielding ‘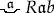 ’. The apparent variable ‘a’ is not a genuine expression of the language but only a typographic feature of the dispersed quantifier sign. Some have seen this as a sign that variables—insofar as they show up in Frege’s approach to quantification—are mere punctuation.
’. The apparent variable ‘a’ is not a genuine expression of the language but only a typographic feature of the dispersed quantifier sign. Some have seen this as a sign that variables—insofar as they show up in Frege’s approach to quantification—are mere punctuation.
The advantages of Fregean over Tarskian predicate logic are due to the former’s treating variables not as meaningful lexical items, but as mere marks of punctuation, similar to parentheses. (Wehmeier 2018: 1)
It has been pointed out that even this modest appearance of variables is unnecessary, cf. Potter (2020: 38). There is a tradition issuing independently from Quine and Bourbaki of typographically writing quantified formulae without explicit variables at all (see Quine 1940/1981: 69–70 and Bourbaki 1954).26 Rather than devices such as ‘ ’ marking the positions bound to the quantifier, this approach manually connects the bound positions to the quantifier sign. Kaplan motivates the position as follows:
We need no variables. We could permit gaping formulas (as Frege would have had it) and use wiring diagrams to link the quantifier to its gaps and to channel in values. (Kaplan 1986: 244).
The suggestion is to render a quantified formula such as as the following wire diagram:
This approach fully identifies alphabetic variant quantified formulae and not merely predicate abstracts. This has been taken by many to be an ultimate vindication of the Fregean approach.27
. . . if we adopt the Quine-Bourbaki notation, then we will not even be able to ask whether typographically distinct variables like ‘ ’ and ‘ ’ have different ‘semantic roles’. (Button & Walsh 2018: 14)
. . . variables could be completely eliminated from Fregean predicate logic in favor of the graphical “bonds” once proposed by Quine as a means to indicate the dependence of argument positions on outlying quantifiers. (Wehmeier 2018: 215)
However, we see things differently. Variables do not reside in the typographic presentation of quantified formulae or complex predicates, but in the syntactic derivations of those quantified formulae or complex predicates. The identification of alphabetic variant quantified formulae or complex predicates does nothing to relieve the tension between truth and reference centrality and compositionality.
In particular, Fregeans must still offer a syntactic derivation of quantified formulae and complex predicates. For example, in the derivation of a quantified formula such as
the derivation of the complex predicate ‘ ’ still runs by way of applying a syntactic operation to a name and a sentence (e.g., and , or and , or and , etc.). And then Π is applied to the result as follows:
For such an operation to be compositional, the name cannot denote its referent and the sentence cannot denote its truth-value for all of the reasons we have already (perhaps tediously) enumerated. The reasons are essentially the same as we saw in §3.2. The syntactic identification of alphabetic variants doesn’t help. For example, the left-hand sides of the following ought to be distinct, but their right-hand sides would be equivalent, if and co-refer.28
A critic might suggest that we are missing the significance of the identification of alphabetic variants on the Fregean approach, because we wrongly suppose that compositionality requires that the semantic value of a complex expression is determined by the semantic values of the expressions that occur in its derivation rather than by the semantic values of its “parts”.29 We follow the standard characterization of compositionality, which demands that the denotation of a derived expression is determined by the denotations of the expressions from which it is syntactically derived (cf. Pagin & Westerståhl 2010). The critic would argue that the denotation of a derived expression must be a function of the denotations of the parts of the derived expression. Because the name and the sentence are not parts of quantified sentence the critic insists that one cannot draw conclusions about the denotations of or from the denotation of the quantified sentence.
However, the conception of compositionality that appeals to parthood in this sense (i.e., parts of derived expressions) is insufficiently general to capture Frege’s approach. The outputs of Frege’s syntactic theory, the Begriffsschrift expressions, are (two-dimensional) arrays of symbols. But, since it may happen that one and the same Begriffsschrift expression can be constructed in more than one way, the components of the array do not reflect the syntactic derivation or semantic evaluation of the expressions that Frege offers. Moreover, they simply lack sufficient structure to calculate their semantic values without appealing to their syntactic derivations.30 To give one example: Frege syntactically derives a formula that we might represent as ‘ ’ by first deriving ‘ ’ from the dyadic predicate ‘ ’ and a name ‘ ’. He then removes occurrences of ‘ ’ to yield the monadic predicate ‘ ’, which is fed into the quantifier ‘ ’, resulting in ‘ ’.31 In the resulting formula, it is not clear whether the monadic predicate ‘ ’, the dyadic predicate ‘ ’, or both are present as parts. Thus, it’s not clear how to apply the principle of compositionality on the basis of the orthographic parts of the formula ‘ ’. But this is not a problem. What matters to the semantic evaluation of a formula is its syntactic derivation.32
So on the common, general conception of compositionality we are concerned with, the semantic value of a complex expression need not be determined by the semantic values of its literal parts and their arrangements (after all, formulae may be Gödel numbers). Rather, the semantic value of a complex expression is determined by the semantic values of the expressions from which it is derived and the semantic significance of the derivation rule. This conception of compositionality is common in contemporary formal semantics (cf. Pagin & Westerståhl 2010).
The two ways of talking about compositionality are not actually opposed. Rather, the conception of compositionality in terms of the parts of an expression agrees with the derivational conception of compositionality, whenever the parts of an expression mirror its syntactic derivation. Thus, the part-whole conception of compositionality is a special case of the general, derivational conception of compositionality. Its range of application is restricted to languages where the output formula has constituents that do match its derivation.33 Evaluated by the standard of compositionality appropriate to Frege’s syntactic theory of Basic Laws §30, we believe—contrary to Dummett, Evans, etc.—that the Fregean approach does not reconcile compositionality with truth and reference centrality.
4. Contemporary Fregeans: Accepting the Dilemma
We have examined the three elements of the Fregean approach to quantification: F1–F3. We have argued that none of these elements releases the Fregean from the dilemma faced by the Tarskian: abandon either truth and reference centrality or compositionality. In the case of F1, we saw that even if quantifiers are predicates of predicates, the Fregean is still tasked with constructing complex predicates in the syntactic derivations of quantified formulae. Standard approaches to this construction invoke Tarskian variables. In the case of F2, we examined Frege’s proposal that complex predicates result from applying a syntactic rule to a name and a closed sentence. However, preserving compositionality required abandoning the doctrine that the denotation of the name is its referent and that the denotation of the sentence is its truth-value. For F3, we saw that the calligraphic presentation of the complex predicate has no impact on the underlying semantic issue, even if the presentation identifies alphabetic variants.
We now turn to examine contemporary approaches inspired by Frege. Working through these approaches, we will see that they ultimately accept one or the other horn of the dilemma. We begin by discussing approaches inspired by Mates (1965) which reject compositionality. We then turn to discuss the approach of Wehmeier (2018) which rejects truth and reference centrality. In neither case are the resources deployed somehow advantageous or more conservative than those deployed by the Tarskian.
4.1. Rejecting compositionality
Frege syntactically analyzes a quantificational statement—which we notate as —as deriving from a quantifier and a complex predicate. The complex predicate is derived by applying a syntactic operation to a name and sentence —Frege would represent the output of the operation as . In Grundgesetze (§31), Frege offers suggestive rules for determining the denotation of the complex predicate and in turn the quantified statement. In particular, Frege proposes that is true if is true for every argument. He then suggests that is true for every argument if and only if is true for every name . Such passages suggest a substitutional rendering of the abstraction rule and quantification more broadly. For example, Dummett says that on Frege’s view “[i]n the case of a complex predicate, the notion of the predicates’ being true or false of an object is derivative from that of the truth or falsity of the sentence which results from filling the argument place of the predicate with some name of the object” (Dummett 1973: 405, cf. 521ff.; see also Evans 1977 and Heck 2012: 64).
These glosses on Frege’s view have been taken to suggest a substitutional reading where the clause for quantification (building in abstraction) would be as follows:
Substitutional Quantification Rule:
Although certain passages of Frege point towards such a clause, Frege’s intentions here have been an issue of controversy (see, e.g., Stevenson 1973).34 Interpreting Frege substitutionally is in tension with Frege’s insistence that functions have a value for every possible argument—unless it is assumed that every object has a name (Heck 2012: 56–57; Dummett 1973: 17–19). We won’t weigh in on the inter- pretative issue, but it seems clear that insofar as a Fregean acknowledges unnamed objects they ought not advocate for the simple substitutional quantification rule.35
Benson Mates’s textbook treatment of first-order logic from the 1960’s develops Frege’s approach in a modern, model-theoretic setting (Mates 1965); cf. Evans (1977: 473–77), Bostock (1997: 84–86), and Heck (2012: 53–64). While model- theoretic semantics is absent from, and possibly even in conflict with, Frege’s own program, contemporary semantic theories in a Fregean tradition often make use of models.36 A model is an interpretation of the basic expressions of the language. The interpretation of a name is an individual and the interpretation of an atomic -ary predicate is a set of -tuples, . Each model gives a model-relative denotation function for every expression of the language.
Mates offers a simple model-theoretic semantics for the quantifier-free sentences. He then offers recursive truth conditions of quantified sentences based on the interpretations assigned ultimately to the quantifier-free sentences. The approach is broadly Fregean because the semantic evaluation of quantified sentences reduces to the semantic evaluation of closed sentences rather than open sentences. It thus appears that these approaches “run their recursion directly on truth” (Evans 1977: 475) and thereby preserve truth and reference centrality.
Mates’s treatment of predicate logic has a standard Tarskian syntax with variables, where quantifiers, such as ‘ ’, are sentential connectives (see §2). Yet, unlike Tarski, Mates does not appeal to variable assignments in the definition of truth for quantified sentences. In fact, Mates’s semantics doesn’t interpret the variables and open sentences at all. Instead, Mates’s strategy provides the semantics of quantified sentences via the reinterpretation of names and closed sentences. The semantics of the quantified sentences are given in terms of reinter- pretations of certain quantifier-free sentences. Namely, those that are related to the (open) formulae embedded under the quantifier by substitution of a name for the occurrences of a variable (see Mates 1965: 54–63). This is carried out in terms of what Mates calls -variant models:
Definition. A model is a -variant of ′ iff and ′ differ at most in what they assign to the name .
Given the notion of a -variant model, a quantified sentence is true in a model if and only if for the first name that doesn’t occur in the sentence is true in every -variant model ′. Or to keep in line with the notation we have been employing, where is the first name that doesn’t occur in , Mates’s rule is as follows:
Mates’s Rule:
Although this semantics may lay claim to preserving truth and reference centrality, it obviously fails to preserve compositionality. In particular, the semantic evaluation of a quantified sentence such as does not proceed by way of the denotation of from which it is derived. Indeed, this formula is given no interpretation in the model.37
While Mates’s particular implementation of his approach is obviously non-compositional, perhaps the appeal to model relativity can be used to restore compositionality.38 Maybe Mates went wrong by assuming that quantified sentences are syntactically derived along Tarskian lines from variables and open sentences while he proposed to semantically evaluate them in terms of related closed sentences. The Fregean syntactic strategies discussed above based on F1, F2, and F3, might aid us in rehabilitating the Fregean semantics.
This approach analyses a quantified sentence as derived from a quantifier and a complex predicate . The complex predicate syntactically derives from an abstraction rule applied to name and closed sentence . A semantic approach similar to that offered by Mates could be developed to offer a model-relative interpretation of the complex predicate in terms of model-relative interpretations of the closed sentence . The model-relative denotation of a predicate abstract is the function that takes an object o and returns true if and only if is true relative to a model differing from only by assigning object o to the name .
Model-Relative Abstraction Rule:
This semantic clause recursively assigns denotations to all predicate abstracts relative to a model in terms of model relative denotations of the basic expressions. One might hope that there is no difficulty in preserving compositionality while holding onto truth and reference centrality.
Closer inspection dashes this hope. Since we have introduced explicit model relativity, we must talk in terms of the model-relativized versions of the principles at play in the dilemma.
model-relative truth and reference centrality: The denotation in a model of a term is an object and the denotation in a model of a sentence is a truth-value.
We must also speak of a language being compositional relative to a model. If the language is compositional relative to a model, then the denotation of a derived expression relative to model is a function of the denotations of the expressions from which it is immediately derived relative to model . Thus, where is a syntactic rule, compositionality relative to a model says the following:
model-relative compositionality:
If the Fregean semantics on offer accepts model-relative truth and reference centrality, it violates model-relative compositionality. To see this compare the model relative denotations of the two abstracts considered above, and . These have different model-relative denotations according to the present Fregean semantics, as can be seen from (i).
(i)
But supposing that , it would follow that (ii).
(ii)
Thus, and differ only by the substitution of expressions— and —with the same model-relative denotation. Even when placed in the model-theoretic setting, the Fregean still faces the choice between truth and reference centrality on the one hand and compositionality on the other—when those are stated in the appropriate model-relative way.
4.2. Rejecting truth and reference centrality
We have argued that neither Mates’s -variant approach nor model-theoretic approaches which might look to Mates for their inspiration allows the Fregean to preserve compositionality. Some Fregeans regard this cost as too high. For example, Wehmeier acknowledges that “[t]he principal challenge in developing Fregean predicate logic is the construction of a compositional semantics” (2018: 214).
To offer a compositional Fregean semantics, Wehmeier shifts his semantic perspective. Rather than offering a denotation relative to a model , Wehmeier offers an absolute, but model-sensitive, denotation for every expression of the language. Thus, an atomic predication will not receive a separate denotation for each model . Instead, the denotation of the sentence will be a function which takes a model as input and outputs the truth-value of the sentence on that model.
These model-sensitive denotations allow Wehmeier to retain compositionality even for the hard case of predicate abstraction. The denotation of a complex predicate depends on the referent of and truth-value of relative to a range of other models. For any model , the denotation of is true on of an object if and only if is true relative to a model that differs from only by assigning to the object . In symbols,
Fregean Abstraction Rule:
Since the semantics is given in terms of the richer model-sensitive values, the counterexamples to compositionality above will be blocked.
While Wehmeier’s semantics is compositional, it flagrantly violates truth and reference centrality. Rather than offering truth-values as the denotations of sentences and objects as the denotations of names, Wehmeier offers functions from models onto truth-values and onto objects, respectively.
. . . the Fregean meanings we are about to construct will . . . be functions defined on the class of all models; indeed, the Fregean meaning. . . of any linguistic item is going to be the function that maps any model to the reference of s in . (Wehmeier 2018: 224)
For example, the denotation of a name will be the function that maps a model to the value of in that model. In symbols: . The denotation of a sentence will be a function from models to truth-values. The denotation of a name, then, will clearly not be an object, and the denotation of a sentence will not be a truth-value. Moreover, Wehmeier explicitly accepts the consequence that distinct names never have the same denotation (Wehmeier 2018: 234).39
Wehmeier is correct that one can retain compositionality by abandoning truth and reference centrality. Indeed, that is what the Tarskians have done (cf. §2.2) by treating the denotation of a term as a function from assignments to objects and the denotation of a sentence as a function from assignments into truth-values. Comparing the semantic clauses for predicate abstraction on each approach, the difference appears to lie (i) in the appeal to letters from the earlier half of the alphabet rather than the latter half and (ii) in the substitution of for .
Fregean Abstraction Rule:
Tarskian Abstraction Rule:
Wehmeier’s clause for predicate abstraction seems to us to be no more than a typographic variant of the Tarskian. A model is an assignment function written in Gothic script. Thus, the model shifting approach should be construed as a form of variabilism, as discussed above.
Wehmeier (2018: 247) argues that his proposal is a more conservative rejection of truth and reference centrality. He points out that in the model-theoretic setting every approach, whether Fregean or Tarskian, involves “a dependency of meanings on models”. He argues that the denotation of an expression must be model sensitive in order to differentiate the meanings of the sentences and , where is empty. The crucial difference between models and assignment functions for Wehmeier is that models reinterpret the predicate constants whereas assignment functions do not. Thus, and will be true in different models and will not have the same model-sensitive meaning.
Wehmeier is correct that in classical presentations of Tarskian predicate logic, an assignment function reinterprets only the individual variables and not the upper case letters that act as predicates. However, the reason assignment functions do not reinterpret the predicates in these presentation of Tarskian first-order logic is that the logic is first-order. In particular, there is no binding of predicate variables. By way of contrast, standard presentations of second-order logic—for instance, Shapiro (1991: 72)—do allow assignment functions to interpret predicate letters. Assignments—so construed—can do all of the theoretical work that Wehmeier assigns to models. This is perhaps why Tarski himself appeals to assignment functions in his early definition of logical consequence.40 Nothing prohibits one from saying with Tarski (1936/1956b) that models are assignments functions. A model is an assignment function that reinterprets not only the terms but also the predicate letters. Thus, there is no need to introduce both assignment and model sensitivity and Wehmeier’s semantics is not more conservative than Tarski’s.
5. Conclusion
While the Tarskian approach to quantification, with its explicit use of variables, faces a number of standard objections, we’ve argued that, despite appearances to the contrary, the Fregean approach is open to the exact same objections. Insofar as the Fregean can offer a compositional semantic treatment of quantification they—like the Tarskian—must rely on variables. In fact, we have argued that developing a fully compositional semantics in the tradition of Frege leads to variabilism: the view that names are variables.
It is worth noting that these results have significant consequences for our understanding of Frege’s puzzle (Frege 1892/1960). Assuming compositionality, Frege argued that if two names such as ‘Hesperus’ and ‘Phosphorus’ denote the same thing, then the sentences ‘Hesperus is Hesperus’ and ‘Hesperus is Phospho- rus’ co-denote as well. Frege found this puzzling because the two sentences have different cognitive values. He therefore posited that expressions have senses in addition to their customary denotations. Although ‘Hesperus’ and ‘Phosphorus’ agree in denotation, they differ in sense, as do the sentences ‘Hesperus is Hesperus’ and ‘Hesperus is Phosphorus’. But given our arguments above, Frege’s theory of quantification already forces a choice: either the denotations of ‘Hesperus’ and ‘Phosphorus’ differ in order to provide a compositional account of quantification or the denotation of a sentence is not a function of the denotations of the names. Therefore, the need to reject either truth and reference centrality or compositionality to save Fregean theories of quantification undermines the argument for the introduction of sense.
An outstanding issue is that names do not substitute salva veritate under a belief report. Frege’s response is to introduce the doctrine of “reference shift”: expressions embedded under belief ascriptions denote their customary senses rather than their customary referents.41 However, the results of this paper open up another possibility: the belief operator could be sensitive to the semantic difference between proper names needed to account for the theory of quantification. This solution would bring the Fregean theory of quantification fully in line with recent variabilists who treat proper names as Tarskian variables. On these approaches, distinct proper names have different denotations. Substitution failures in belief ascriptions can be accounted for if the belief operator is sensitive to this difference in denotations.42
Acknowledgements
For comments, thanks to Wolfgang Schwarz, Fiona Doherty, Tim Button, Max Cresswell, Derek Ball, William Stirton, Kai Wehmeier, Robert May, Øystein Linnebo, John MacFarlane, Albert Visser, Bruno Jacinto, Bjørn Jespersen, Robert Trueman, and all the anonymous referees. Thanks also to audiences at Lingnan University, the University of Hong Kong, Utrecht University, Arché’s Language and Mind Seminar, the Workshop on Identity and Quantification at the University of Birmingham, and the 2021 Pacific APA.
Notes
- The so-called “antinomy of the variable” appeals to conflicting pressures to say of two distinct variables and that they are semantically alike but also that they are semantically different. See Fine (2003), cf. Jacobson (1999: 127), and see Pickel and Rabern (2016) for extended discussion. While the antinomy of the variable per se is not our primary concern here, our thesis casts doubt on the claim than the Fregean is better placed than the Tarskian to address the antinomy. ⮭
- To simplify discussion we ignore function letters and complex singular terms, which Pickel (2010) argues cause additional difficulties for Fregean syntax. ⮭
- The point of this convention will become apparent later in connection with Frege’s syntax. To cut down on quotation marks we also employ the convention that atomic expressions can be used to refer to themselves. Given these conventions on the metalanguage and on use/mention, and are names, is a predicate, and is a formula. Note that is a formula, and in fact . But is not a formula, instead it refers to one. That is, is a metalanguage description of an object language formula, namely ; likewise is a formula and refers to it; is a formula and refers to it. The same convention applies when quantification and abstraction are introduced, so, e.g., is a formula referred to by , is a predicate referred to by , and is a predicate referred to by , and so on. ⮭
- See Montague (1970), Montague (1973), Lewis (1970), Dowty, Wall, and Peters (1981). For discussion see Partee (1984) and Hodges (2001). Compositionality can be stated equivalently given standard assumptions (cf. Pagin & Westerståhl 2010) as the principle that the denotation of a complex expression is the result of applying a function to the denotations of the expressions from which it syntactically derives: For every syntactic rule there is a semantic operation such that ⮭
- Frege says: “the truth value of a sentence remains unchanged when an expression is replaced by another having the same reference” (Frege 1892/1960: 64). Frege’s specific commitments on compositionality, especially in connection to the context principle, remain a matter of dispute (see Janssen 2001; Pelletier 2001 and references therein, including classic discussions in Dummett 1973). ⮭
- Of course, for Frege a sentence has a truth-value as its referent, e.g., Frege (1891/1997: 137). ⮭
- The basic style of approach goes back to Tarski (1935/1956a), and was refined in later works such as Tarski and Vaught (1957). See Hodges (2014) for an overview. There are many textbooks that follow the Tarskian approach including Tarski (1941), Hunter (1971), Machover (1996), Bergmann, Moor, and Nelson (2009), Barker-Plummer, Barwise, and Etchemendy (2011), etc., and including textbook introductions to natural language semantics such as Heim and Kratzer (1998). ⮭
- See Janssen (1997) and Hodges (2014). This is the approach that is connected to Tarksi’s algebraization of first-order logic. See Monk (1976: 219–30) and Henkin, Monk, and Tarski (1971) on cylindrical algebras. ⮭
- One can easily re-construe what we say here in terms of the standard models , where is the domain and assigns appropriate values to the -place predicates and names. Note that Tarski’s earlier semantics in, e.g., Tarski (1935/1956a) is more in line with the way presented here, whereas the more standard presentation occurs later, perhaps most explicitly in Tarski and Vaught (1957). See discussion in Etchemendy (1988a) and Hodges (2014). We discuss model-theoretic approaches more explicitly in §4, especially in connection with Mates (1965) and with Wehmeier’s (2018) model-theoretic construal of Fregean semantics. ⮭
- Or look at it in terms of the functional understanding of compositonality. For quantification we have the following: . But consider and and assume, , so that . Thus, ⮭
- A background assumption here is that truth-values are just the True and the False. In particular, it is assumed that a truth-value is not a function from assignments to {the True, the False}—and more generally a truth-condition (or proposition) is not a function on assignments. Likewise, it is assumed that the referent of “Gottlob” is a man, not a function from assignments to men. If truth-values and reference were re-construed so they were functions on assignments, then, of course, the core tension would dissolve. One can make any system that is compositional in terms of intensions compositional in terms of “extension” so long as one is willing to re-construe the “intensions” as the “extensions” (see Lewis 1974). ⮭
- For recent advocates of propositional centrality see King (2003), Schaffer (2021), and Glanzberg and King (2020). Others have argued that compositional semantics must displace content for semantic value (Lewis 1980), see, e.g., Ninan (2010), Rabern (2012; 2017), Recanati (2018), and references therein. King (2007: Appendix) attempts to offer a theory of quantification that incorporates elements of the Fregean view discussed below in order to (i) guarantee that propositions have semantic primacy and (ii) deliver compositionality. Yet, Yli-Vakkuri (2013) convincingly argues that King’s approach is not compositional for reasons similar to those we offer to show that the centrality of truth is incompatible with compositionality. See also Rabern (2013), Pickel and Rabern (2016), and Pickel and Rabern (2021). ⮭
- Actually, to ensure genuine compositional compliance the last clause requires a small amendment. We should only appeal to the semantic value of a variable , namely , instead of the variable itself. This is easily remedied. To do so we introduce the function , which maps the semantic value of a variable to the variable itself. In particular, = the variable such that for any assignment Since for any variables and if then is well-defined, and will have the result that for any variable See Zimmermann and Sternefeld (2013: 242) for extended discussion of this trick, which will be required by fully compositional implementations of Frege-inspired approaches as well. With this complication in place we can specify the fully compositional clause as follows: ⮭
- Compare to Salmon’s (2006b) discussion of proper names as “invariable variables”. ⮭
- See, for example, Yagisawa (1984), Dever (1998), Cumming (2008), Santorio (2012), Pickel (2015), Schoubye (2017; 2020), and Rabern (2021). ⮭
- The natural language sentence ‘everybody envies somebody’ is ambiguous. However, this ambiguity is not important for the main point that Dummett is illustrating. The corresponding formula of Begriffsschrift is unambiguous. ⮭
- If the Gothic letters are ordered, Frege could get by with a single syntactic formation rule for quantification. There is some evidence for this in Frege (1893/2013: §8, Rule 2), where Frege describes the procedure for generating a quantified formula from a complex predicate, saying that if in an argument place is in the scope of a concavity with a given German letter , then for the resulting sentence a distinct German letter (perhaps ) must decorate the new concavity. ⮭
- The problem is acute for sentences containing multiple quantifiers such as ‘everyone loves someone’, which does not result from applying the quantifier phrase ‘someone’ to a simple predicate. The quantifier applies to the complex predicate ‘being such that is such that love them’. ⮭
- See, e.g., Lewis (1970: 43ff.); but also Church (1932), Montague (1970), Cresswell (1973), and Stalnaker (1977). This is standard in connection with generalized quantifier theory, e.g., Barwise and Cooper (1981) implement quantified NPs as sets of sets and include an abstraction operator that combines with a formula to form a set term. For a textbook discussion, see Heim and Kratzer (1998: 189–90). ⮭
- Note that Cresswell’s (1973: 80–87) argument concerning the non-compositionality of can be reproduced in his lambda-categorial language by considering lambda terms such as and . This leads to a violation of Frege’s Principle (as defined on Cresswell’s p. 76), but Cresswell, somewhat surprisingly, never revisits the compositionality principle in connection with the lambda-categorial language. ⮭
- See Lewis (1970: 44–45) and Montague (1970). And see Rabern (2013: 398–400) for discussion. See also Kobele (2010) in connection with natural language syntax-semantics interface. ⮭
- Recall the convention introduced above (see footnote 3) that an instance of is a metalanguage descriptions of an object language expression rather than an object language expressions itself. So, for example, ‘ ’ and ‘ ’ are metalanguage descriptions of object language predicates, whereas and themselves are object language predicates, since . For all we have said it could even be that — this identification of “alphabetic variants” is explicitly considered in the next section. ⮭
- See, for example, Yagisawa (1984), Dever (1998), Cumming (2008), Pickel (2015), and Schoubye (2017; 2020). ⮭
- In other words, assume compositionality, and that Then and so . Contradiction. See also Resnik (1986: 182) and Fine (2003: 615). ⮭
- It seems to us that Wehmeier (2021) is misled by a conflation between the parts of a derived expression (such as elements of a string) and the inputs to a syntactic derivation. For example, he insists that a syntactic deletion rule (such as Δ) is not a “syntactic mode of composition”, and he then draws semantic conclusions from the insistence that gaps “are mere absences of syntactic material”. Similar remarks occur in Wehmeier (2018). ⮭
- Peirce’s diagrammatic representation of quantificational logic in terms of “existential graphs” shares this feature of linking argument positions with wires. See Peirce (1903: 15–23). ⮭
- The syntax of Bourbaki (1954) has a primitive “gap” symbol □, alongside the other primitive symbols such as negation, disjunction, and the Hilbert operator. Bourbaki understand formulae as strings of symbols with links between the occurrences of symbols. Thus, a Bour- bakian formulae could be construed as a string of symbols paired with an equivalence relation on positions. Importantly for us, Bourbaki syntactically derive quantified formulae (or epsilon terms) from a term and a formulae. See Mathias (2002) and Grimm (2013) for discussion of Bourbaki’s syntax. ⮭
- Note that there is nothing to prohibit a Tarskian from also identifying alphabetic variant quantified formulae or complex predicates. The Tarskian would syntactically derive a quantified formula such as by applying the rule to the variable and the open sentence . The Tarskian then adds that the rule is a transformation rule outputting the relevant variable-free string of marks so that the formula is identical to the formula , which is derived by applying the rule to an open sentence and . Lewis (1970: 45–46) proposed such a transformation rule to identify alphabetic variants. And this is now a standard approach in the otherwise Tarskian presentations of the lambda-calculus of functions (see Barendregt 1984: Convention 2.1.12). ⮭
- One such critic might be Wehmeier (2021: 17) who argues that Frege’s deletion operation should not be counted as a semantic composition rule since it involves removing an expression. On our view, what matters is that it is a syntactic derivation rule. That is, the formulae of the Begriffsschrift do not contain as parts all of the expressions that figure in their syntactic derivations, but compositionality requires us to semantically evaluate a formula in terms of the expressions that figure in its syntactic derivation. ⮭
- Note that the fact the the formulae of the Begriffsschrift are two-dimensional is irrelevant to the point we are making here. The point is that expressions that figure in the syntactic derivation of a formula are not recoverable from the output of the derivation. ⮭
- See Frege (1893/2013: §30), where Frege offers this exact derivation. ⮭
- We are running compositionality on expressions in deference to the Fregeans. However, there is a conception of compositionality that can restore the connection between parthood and syntactic derivation (see Hodges 2001). The semantic value of an expression with structured description is determined by the semantic values of the expressions represented by the parts of . Thus, is a structured description of a formula. The parts of this structured description correspond to expressions that occur in the derivation of the formula it represents. The semantic value of the formula picked out by the description is determined by the semantic values of the expressions that occur in the derivation of the formula. Thus, this conception of compositionality connects the meaning of a formula to the parts of its structured description rather than to the parts of the formula itself. Appealing to this alternative conception of compositionality does not alter the dialectic of the paper. In particular, appealing to structured descriptions does not allow the Fregean to claim that they have eliminated variables unless they have also eliminated variables from the structured descriptions. Thanks to an anonymous referee for Ergo for pointing out this alternative. ⮭
- Many contemporary semanticists—under the influence of the Katz-Postal hypothesis (Katz & Postal 1964)—do believe that there is a level syntactic representation for natural language satisfying this description. However, what’s interesting about the Fregean approach is that the assumption is not satisfied, making the more general, derivational conception of compositionality the appropriate standard. In this respect, the Fregean approach agrees with contemporary approaches to semantics that likewise disavow a level of LF and attempt to offer a directly compositional semantics for surface forms in terms of their syntactic derivations (cf. Jacobson 2014). ⮭
- See also Heck (1997), Heck (2012: 53–64), Boolos (1998: 225–27), and Dummett (1973: 521–28). ⮭
- Boolos, Burgess, and Jeffrey go so far as to call the substitutional clause above “a simple, tempting, and wrong approach to defining truth for the case of quantification” (2007: 116). ⮭
- See Blanchette (2012) and surrounding literature on the Frege-Hilbert Controversy, e.g., Doherty (2017) and references therein. ⮭
- This is a key feature shared with substitutional quantification (see Kripke 1976: 330). ⮭
- There are slight variants to Mates’s approach that appeal to “auxiliary names” or extensions of the language such as Heck (2012: 275–82), which are also not compositional. Button and Walsh (2018: 15–19) develop a Mates-style approach that “seems to provide a truly compositional notion of meaning” (2018: 21). However, all they mean by this is that the semantic clause to construct a quantified sentence from a quantifier and a complex predicate is compositional. They do not offer a compositional semantics for complex predicates. ⮭
- Wehmeier (2018; 2021) insists that his Fregean approach is compositional, while, in contrast to the Tarskian approach, employs an ontology where the types “all live in the extensional type hierarchy”. This cannot be maintained. But, Wehmeier is clear that the theory is not compositional in terms of these extensional types—instead compositionality reigns at the level of “Fregean intensions” (i.e., functions from models to extensions in models)—so he is explicitly denying truth and reference centrality. ⮭
- See Etchemendy (1988a) and Etchemendy (1988b). Of course without varying the domain of quantification a sentence such as would come out as a logical truth. See García-Carpintero (1992). ⮭
- This idea has been extended to quantification in Salmon (2006a) and Glanzberg and King (2020). See Pickel and Rabern (2021) for discussion. ⮭
- See, e.g., Cumming (2008), Santorio (2012), Pickel (2015), Ninan (2018), and Rabern (2021). ⮭
References
1 Barendregt, Hendrik Pieter (1984). The Lambda Calculus: Its Syntax and Semantics. Elsevier.
2 Barker-Plummer, Dave, Jon Barwise, and John Etchemendy (2011). Language, Proof, and Logic (Vol. 2). CSLI Publications.
3 Barwise, Jon and Robin Cooper (1981). Generalized Quantifiers and Natural Language. Linguistics and Philosophy, 4(2), 159–219.
4 Bergmann, Merrie, James Moor, and Jack Nelson (2009). The Logic Book. McGraw-Hill.
5 Blanchette, Patricia A. (2012). Frege’s Conception of Logic. Oxford University Press.
6 Boolos, George (1998). Logic, Logic, and Logic. Harvard University Press.
7 Boolos, George, John P. Burgess, and Richard C. Jeffrey (2007). Computability and Logic (5th ed.). Cambridge University Press.
8 Bostock, David (1997). Intermediate Logic. Oxford University Press.
9 Bourbaki, Nicolas (1954). Éléments de mathématique: Théorie des ensembles. Hermann.
10 Button, Tim and Sean Walsh (2018). Philosophy and Model Theory. Oxford University Press.
11 Carnap, Rudolph (1947). Meaning and Necessity: A Study in Semantics and Modal Logic. University of Chicago Press.
12 Carnap, Rudolph (1959). The Logical Syntax of Language. University of Chicago Press. (Original work published 1934)
13 Chomsky, Noam (1957). Syntactic Structures. Mouton.
14 Church, Alonzo (1932). A Set of Postulates for the Foundation of Logic. Annals of Mathematics, 33(2), 346–66.
15 Cresswell, Max (1973). Logics and Languages. Methuen.
16 Cumming, Samuel (2008). Variabilism. Philosophical Review, 117(4), 525–54.
17 Dever, Josh (1998). Variables. Dissertation, University of California, Berkeley.
18 Dever, Josh (1999). Compositionality as Methodology. Linguistics and Philosophy, 22(3), 311–26.
19 Doherty, Fiona (2017). Hilbert on Consistency as a Guide to Mathematical Reality. Logique et Analyse, 60(237), 107–28.
20 Dowty, David, Robert Wall, and Stanley Peters (1981). Introduction to Montague Semantics. Synthese Language Library, Vol 11. Reidel.
21 Dummett, Michael (1973). Frege: Philosophy of Language. Gerald Duckworth.
22 Dummett, Michael (1981). The Interpretation of Frege’s Philosophy. Harvard University Press.
23 Etchemendy, John (1988a). Tarski on Truth and Logical Consequence. The Journal of Symbolic Logic, 53(1), 51–79.
24 Etchemendy, John (1988b). Models, Semantics and Logical Truth. Linguistics and Philosophy, 11(1), 91–106.
25 Evans, Gareth (1977). Pronouns, Quantifiers, and Relative Clauses (I). Canadian Journal of Philosophy, 7(3), 467–536.
26 Fine, Kit (2003). The Role of Variables. The Journal of Philosophy, 100(12), 605–31.
27 Frege, Gottlob (1960). On Sense and Reference In P. Geach and M. Black (Eds.), Translations from the Philosophical Writings of Gottlob Frege (56–78). Blackwell. (Original work published 1892)
28 Frege, Gottlob (1997). Function and Concept. In Michael Beaney (Ed.), The Frege Reader (130–48). Blackwell Oxford. (Original work published 1891)
29 Frege, Gottlob (2013). Gottlob Frege: Basic Laws of Arithmetic. P. A. Ebert and M. Rossberg with C. Wright (Eds. and Trans.). Oxford University Press. (Original work published 1893)
30 García-Carpintero, Manuel (1992). The Grounds for the Model-Theoretic Account of the Logical Properties. Notre Dame Journal of Formal Logic, 34(1), 107–31. doi: http://doi.org/10.1305/ndjfl/1093634568
31 Glanzberg, Michael and Jeffrey C. King (2020). Binding, Compositionality, and Semantic Values. Philosophers’ Imprint, 20(2), 1–29.
32 Grimm, José (2013). Implementation of Bourbaki’s Elements of Mathematics in Coq: Part One, Theory of Sets. Research Report RR-6999. INRIA.
33 Heck, Richard Kimberly (1997). Grundgesetze der Arithmetik I §§29–32. Notre Dame Journal of Formal Logic, 38(3), 437–74. (Originally published under the name “Richard G. Heck, Jr.”)
34 Heck, Richard Kimberly (2012). Reading Frege’s Grundgesetze. Oxford University Press. (Originally published under the name “Richard G. Heck Jr.,”)
35 Heim, Irene and Angelika Kratzer (1998). Semantics in Generative Grammar. Blackwell.
36 Henkin, Leon, Donald Monk, and Alfred Tarski (1971). Cylindric Algebras: Part I. North-Holland.
37 Hodges, Wilfrid (2001). Formal Features of Compositionality. Journal of Logic, Language and Information, 10(1), 7–28.
38 Hodges, Wilfrid (2014). Tarski’s Truth Definitions. In Edward N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy (Fall 2014 ed.). Metaphysics Research Lab, Stanford University. Retrieved from https://plato.stanford.edu/archives/fall2014/entries/tarski-truth/
39 Hunter, Geoffrey (1971). Metalogic: An Introduction to the Metatheory of Standard First Order Logic. University of California Press.
40 Jacobson, Pauline (1999). Towards a Variable-Free Semantics. Linguistics and Philosophy, 22(2), 117–85.
41 Jacobson, Pauline (2014). Compositional Semantics: An Introduction to the Syntax/Semantics Interface. Oxford University Press.
42 Janssen, Theo M. V. (1997). Compositionality. In J. van Benthem and A. ter Meulen (Eds.), Handbook of Logic and Language (417–73). Elsevier.
43 Janssen, Theo M. V. (2001). Frege, Contextuality and Compositionality. Journal of Logic, Language and Information, 10(1), 115–36. http://doi.org/10.1023/A:1026542332224
44 Kalish, Donald and Richard Montague (1964). Logic: Techniques of Formal Reasoning. Oxford University Press.
45 Kaplan, David (1986). Opacity. In Lewis Edwin Hahn and Paul Arthur Schilpp (Eds.), The Philosophy of W. V. Quine (229–89). Open Court.
46 Katz, Jerrold and Paul Postal (1964). An Intergrated Theory of Linguistic Description. The MIT Press.
47 King, Jeffrey C. (2003). Tense, Modality, and Semantic Values. Philosophical Perspectives, 17(1), 195–246.
48 King, Jeffrey C. (2007). The Nature and Structure of Content. Oxford University Press.
49 Kobele, Gregory M. (2010). Inverse Linking via Function Composition. Natural Language Semantics, 18(2), 183–96.
50 Kripke, Saul A. (1976). Is There a Problem about Substitutional Quantification? In Gareth Evans and John McDowell (Eds.), Truth and Meaning (324–419). Oxford University Press.
51 Larson, Richard and Gabriel Segal (1995). Knowledge of Meaning: An Introduction to Semantic Theory. MIT Press.
52 Lewis, David (1970). General Semantics. Synthese, 22(1), 18–67.
53 Lewis, David (1974). ’Tensions. In Milton K. Munitz and Peter K. Unger (Eds.), Semantics and Philosophy (49–61). New York University Press.
54 Lewis, David (1980). Index, Context and Content. In S. Kanger and S. Ohman (Eds.), Philosophy and Grammar (79–100). Reidel.
55 Machover, Moshé (1996). Set Theory, Logic and Their Limitations. Cambridge University Press.
56 Mates, Benson (1965). Elementary Logic. Oxford University Press.
57 Mathias, Adrian R. D. (2002). A Term of Length 4 523 659 424 929. Synthese, 133(1/2), 75–86.
58 Monk, J. Donald (1976). Mathematical Logic. Graduate Texts in Mathematics, Vol. 37. Springer.
59 Montague, Richard (1970). Universal Grammar. Theoria, 36(3), 373–398.
60 Montague, Richard (1973). The Proper Treatment of Quantification in Ordinary English. Approaches to Natural Language, 49, 221–42.
61 Ninan, Dilip (2010). Semantics and the Objects of Assertion. Linguistics and Philosophy, 33(5), 335–80.
62 Ninan, Dilip (2018). Quantification and Epistemic Modality. Philosophical Review, 127(4), 433–85.
63 Pagin, Peter and Dag Westerståhl (2010). Compositionality I: Definitions and Variants. Philosophy Compass, 5(3), 250–64.
64 Partee, Barbara (1984). Compositionality. In F. Landman and F. Veltman (Eds.), Varieties of Formal Semantics (281–311). Foris.
65 Partee, Barbara (2013). The Starring Role of Quantifiers in the History of Formal Semantics. In V. Punčochář and P. Švarný (Eds.), The Logica Yearbook 2012 (113–36). College Publications.
66 Peirce, Charles S. (1903). A Syllabus of Certain Topics of Logic. Alfred Mudge & Son.
67 Pelletier, Francis Jeffry (2001). Did Frege Believe Frege’s Principle? Journal of Logic, Language and Information, 10(1), 87–114.
68 Pickel, Bryan (2010). Syntax in Basic Laws §29–32. Notre Dame Journal of Formal Logic, 51(2), 253–77.
69 Pickel, Bryan (2015). Variables and Attitudes. Noûs, 49(2), 333–56.
70 Pickel, Bryan and Brian Rabern (2016). The Antinomy of the Variable: A Tarskian Resolution. The Journal of Philosophy, 113(3), 137–70.
71 Pickel, Bryan and Brian Rabern (2021). The Myth of Occurrence-Based Semantics. Linguistics and Philosophy, 44, 813–37.
72 Potter, Michael (2020). The Rise of Analytic Philosophy, 1879–1930: From Frege to Ramsey. Routledge.
73 Quine, Willard V. (1981). Mathematical Logic (rev. ed.). Harvard University Press. (Original work published 1940)
74 Rabern, Brian (2012). Against the Identification of Assertoric Content with Compositional Value. Synthese, 189(1), 75–96.
75 Rabern, Brian (2013). Monsters in Kaplan’s Logic of Demonstratives. Philosophical Studies, 164(2), 393–404.
76 Rabern, Brian (2017). A Bridge from Semantic Value to Content. Philosophical Topics, 45(2), 181–207.
77 Rabern, Brian (2021). Binding Bound Variables in Epistemic Contexts. Inquiry: An Interdisciplinary Journal of Philosophy, 64(5–6), 533–63.
78 Recanati, François (2018). From Meaning to Content. In Derek Ball and Brian Rabern (Eds.), The Science of Meaning: Essays on the Metatheory of Natural Language Semantics (113–37). Oxford University Press.
79 Resnik, Michael D. (1986). Frege’s Proof of Referentiality. In L. Haaparanta and J. Hintikka (Eds.), Frege Synthesized (177–95). D. Reidel.
80 Salmon, Nathan (2006a). A Theory of Bondage. The Philosophical Review, 115(4), 415–48.
81 Salmon, Nathan (2006b). Pronouns as Variables. Philosophy and Phenomenological Research, 72(3), 656–64.
82 Santorio, Paolo (2012). Reference and Monstrosity. Philosophical Review, 121(3), 359–406.
83 Schaffer, Jonathan (2021). Confessions of a Schmentencite: Towards an Explicit Semantics. Inquiry: An Interdisciplinary Journal of Philosophy, 64(5–6), 593–623.
84 Schoubye, Anders J. (2017). Type-Ambiguous Names. Mind, 126(503), 715–67.
85 Schoubye, Anders J. (2020). Names Are Variables. Philosophical Review, 129(1), 53–94.
86 Shapiro, Stewart (1991). Foundations without Foundationalism: A Case for Second-Order Logic. Oxford University Press.
87 Smith, Nicholas J. J. (2017). Truth via Satisfaction? In Pavel Arazim and Tomáš Lávička (Eds.), The Logica Yearbook 2016 (273–87). College Publications.
88 Soames, Scott (2010). Philosophy of Language. Princeton University Press.
89 Stalnaker, Robert (1977). Complex Predicates. The Monist, 60(3), 327–39.
90 Stevenson, Leslie (1973). Frege’s Two Definitions of Quantification. The Philosophical Quarterly, 23(92), 207–23.
91 Tarski, Alfred (1941). Introduction to Logic and to the Methodology of Deductive Sciences. Oxford University Press.
92 Tarski, Alfred (1956a). The Concept of Truth in Formalized Languages. In Logic, Semantics, Metamathematics: Papers from 1923 to 1938 (152–278). Clarendon Press. (Original work published 1935)
93 Tarski, Alfred (1956b). On the Concept of Logical Consequence. In Logic, Semantics, Metamathematics: Papers from 1923 to 1938 (409–20). Clarendon Press. (Original work published 1936)
94 Tarski, Alfred and Robert Vaught (1957). Arithmetical Extensions of Relational Systems. Compositio Mathematica, 13(2), 81–102.
95 Wehmeier, Kai F. (2018). The Proper Treatment of Variables in Predicate Logic. Linguistics and Philosophy, 41(2), 209–49.
96 Wehmeier, Kai F. (2021). Are Quantifiers Intensional Operators? Inquiry: An Interdisciplinary Journal of Philosophy, 64(5–6), 511–32.
97 Yagisawa, Takashi (1984). Proper Names as Variables. Erkenntnis, 21(2), 195–208.
98 Yli-Vakkuri, Juhani (2013). Propositions and Compositionality. Philosophical Perspectives, 27(1), 526–63.
99 Zimmermann, Thomas Ede and Wolfgang Sternefeld (2013). Introduction to Semantics: An Essential Guide to the Composition of Meaning. Walter de Gruyter.