Theodore Sider writes:
I think we ought to make [the following assumption about fundamentality]—what I call “purity”: fundamental truths involve only fundamental notions. When God was creating the world, she was not required to think in terms of nonfundamental notions like city, smile, or candy. . . . Suppose someone claimed that even though cityhood is a nonfundamental notion, in order to tell the complete story of the world there is no way to avoid bringing in the notion of a city—certain facts involving cityhood are rock-bottom. This is the sort of view that purity says we should reject. (2011: 106–7)1
Thus Sider claims that the fundamental truths are “pure” in the sense that they involve only fundamental notions—the fundamental truths are thus not “infected” with non-fundamental notions like city, smile, or candy (2011: 144). The purity of the fundamental truths ensures that one can write the complete “book of the world” without mentioning cities or smiles or candy.
Sider’s formulation of the purity principle presupposes that “truths” and “notions” are the primary bearers of fundamentality and derivativeness. Advocates of grounding, on the other hand, take the primary bearers of fundamentality and derivativeness to be Russellian facts or Armstrongian states of affairs and the worldly particulars, properties, and logical connectives that are their constituents.
For example, consider a concrete particular: electron e. The fact that electron e has some property F, which we can represent using square brackets as [e is F], has electron e and the property of being F as its constituents. For advocates of grounding, entities like electron e and worldly facts like [e is F], rather than linguistic items like truths and notions, are the bearers of fundamentality and derivativeness.
Just as Sider’s principle prohibits derivative notions from being involved in fundamental truths, some advocates of grounding have defended an analogous prohibition against derivative entities being constituents in any fundamental fact. For example, Louis deRosset formulates and endorses the following principle:
CORR “An entity e is fundamental if e’s existence or its possession of some feature is fundamental” (deRosset 2013: 6).
Suppose that entity e is F. And suppose the fact that e is F, which we can represent using square brackets as [e is F], is a fundamental fact. Then CORR entails that entity e itself is a fundamental entity. More generally, deRosset’s CORR principle implies that for any entity x and any property F, if [x is F] is a fundamental fact, then x is a fundamental entity.
Along the same lines, Gideon Rosen says:
Say that a fact is fundamental (or brute) if it does not obtain in virtue of other facts, and that a thing is fundamental if it is a constituent of a fundamental fact. Then we might say that fundamental ontology seeks a catalog of the fundamental things. (Rosen 2010: 112)
Rosen, like deRosset, endorses the purity-like claim that fundamental facts have only fundamental entities or “things” as constituents.
In the same vein, Shamik Dasgupta defends grounding-based formulations of physicalism from the “Siderean worry” that the facts about the explanatory connection between the physical and the non-physical are not themselves “purely” physical.2 And in response to this worry, Dasgupta formulates a version of physicalism according to which all the fundamental facts are purely physical, in the sense that they involve only physical phenomena (Dasgupta 2014: 580–92).3
I take deRosset, Rosen, Dasgupta, and others, to all be endorsing the following non-linguistic version of Sider’s purity principle:4
Purity: no fundamental fact contains a derivative entity as a constituent.
This version of the purity principle—henceforth just “Purity”— prohibits derivative entities from being constituents of fundamental facts. For example, Purity prohibits derivative entities like cities, smiles, and candy from being constituents in any fundamental fact. To use Sider’s metaphor, Purity ensures that the complete “book of the world”—the book detailing all the fundamental facts—makes no reference to derivative entities like cities, smiles, and candy.
This paper has two main conclusions. Its first conclusion is that Purity is false. My argument is a reductio—I argue Purity implies a contradiction and should therefore be rejected. The paper’s second conclusion concerns the so-called “grounding facts” or facts about what grounds what. Purity’s falsity, so I argue, gives us reason to think that some grounding facts are fundamental rather than grounded. I close by arguing that the facts about what grounds composition’s occurrence are particularly good candidates for fundamental grounding facts.
1. Purity and Grounding Grounding
Let a grounding fact be any fact about what partially grounds what and any fact about what fully grounds what. For example, suppose that Socrates fully grounds {Socrates}. Then the following is a grounding fact: [Socrates fully grounds {Socrates}]. Or suppose the fact that p partially grounds [p and q]. Then the following is a grounding fact: [p partially grounds [p and q]]. And so on.
Consider the following thesis about grounding facts:
The Grounding Grounding Thesis (GGT): every grounding fact is fully grounded.
Like Purity, GGT is quite popular among grounding’s advocates. It has been endorsed by, among others, Karen Bennett (2011b), Louis deRosset (2013), Shamik Dasgupta (2014), Kit Fine (2012: 74–80), Michael Raven (2015), and Gideon Rosen (2010: §13). Indeed, virtually all of those who endorse Purity also endorse GGT.5 This is no accident. Rather, those who accept GGT generally do so because they accept Purity.
In a moment, I will present a version of the standard argument that Purity’s truth implies GGT (see Bennett 2011a; Sider 2011; and deRosset 2013). I have two brief clarificatory comments before we begin.
First, I shall use the term “entity” quite broadly, so that concrete particulars, abstract objects, properties, and worldly facts or Armstrongian states of affairs all count as entities. Second, I shall assume that an entity is fundamental if and only if it is ungrounded, and an entity is derivative if and only if it is fully grounded.
Here is the standard argument from Purity to GGT. Consider again the grounding fact [Socrates fully grounds {Socrates}]. This fact has the following entities among its constituents: Socrates, {Socrates}, and the full grounding relation. {Socrates} is a grounded entity. So {Socrates} is a derivative entity. Therefore, the grounding fact [Socrates fully grounds {Socrates}] has at least one derivative entity among its constituents.
Now suppose that Purity is true—no fundamental fact has any derivative entity as a constituent. The grounding fact [Socrates fully grounds {Socrates}] has a derivative constituent. So it is not fundamental. Instead, the grounding fact [Socrates fully grounds {Socrates}] is a derivative entity. An entity is derivative if and only if it is fully grounded. Therefore, the grounding fact [Socrates fully grounds {Socrates}] is itself fully grounded in something else.
I just argued that if Purity is true then the grounding fact [Socrates fully grounds {Socrates}] is fully grounded. Of course, that particular grounding fact was picked arbitrarily. We could have run the same argument, mutatis mutandis, for any other grounding fact whatsoever. Given Purity, facts about what grounds the existence and properties of composite material objects, facts about what grounds conscious mental states, facts about what grounds determinable properties, and so on, all must have a full ground.
Indeed, if Purity is true then even the facts about what partially grounds what are themselves fully grounded. For suppose the conjunctive fact [Socrates and Plato exist] is fully grounded in Socrates and Plato, taken together, but only partially grounded in each man, taken individually. Then the grounding fact [Socrates partially grounds [Socrates and Plato exist]] has a derivative entity, [Socrates and Plato exist], as a constituent. Purity says that no fundamental fact has a derivative constituent. Therefore, the partial grounding fact [Socrates partially grounds [Socrates and Plato exist]] is itself fully grounded in something else.
I have just defended the following conditional: if Purity is true, then GGT is true. No defender of Purity should reject this conditional. For virtually every defender of Purity already accepts it. Indeed, many defenders of Purity accept that conditional precisely because they are persuaded by some version of the above argument.6 I mention this conditional’s uncontroversial status because it will play a key role in my argument against Purity. Indeed, it is that argument’s second premise.
The other two main premises draw the notion of a “groundmate.” Let us say that a grounded entity x has an entity y as its groundmate just in case x is numerically distinct from y, and y is a grounded entity, and there are some entities, the zs, such that x is fully grounded in the zs and y is fully grounded in the zs. In other words, groundmates are distinct grounded entities that share at least one full ground.
I can now state my reductio argument against Purity:
| (1) | Purity is true. | AS |
| (2) | If Purity is true, then GGT is true. | PR |
| (3) | If GGT is true, then there are groundmates. | PR |
| (4) | If Purity is true, then there are no groundmates. | PR |
| (5) | Therefore, if Purity is true, then there are groundmates. | HS 2, 3 |
| (6) | Therefore, there are groundmates. | MP 1,5 |
| (7) | Therefore, there are no groundmates. | MP 1,4 |
| (8) | Therefore, Purity is false. | reductio 1, 6, 7 |
The argument is valid—Purity is assumed for reductio at line 1, from which a contradiction is validly derived at lines 6 and 7. I have already defended Premise 2. I shall defend Premise 3 and Premise 4 in Sections 2 and 3, respectively.
2. GGT and Groundmates
Here is Premise 3:
-
(3)
If GGT is true, then there are groundmates.
My defense of Premise 3 proceeds via conditional proof—I shall suppose that Premise 3’s antecedent is true and then argue from that supposition to the truth of Premise 3’s consequent.
Suppose that GGT is true. Also suppose that there is some arbitrary entity that is either fully or partially grounded in some other entity.7 Then there is at least one grounding fact. According to GGT, every grounding fact is fully grounded. So our arbitrary grounding fact is fully grounded. Now ask: What fully grounds this grounding fact?
There are four extant answers to this question. The first two answers, so I shall argue, straightforwardly entail that our arbitrary grounding fact has a groundmate. So, if either of those two answers is true, then there are groundmates (§2.1–2). I will then argue that the other two answers also lead to groundmates, albeit only in conjunction with a relatively modest first-order assumption about what grounds what (§2.3–6).
2.1. Bottom-Up Particularism
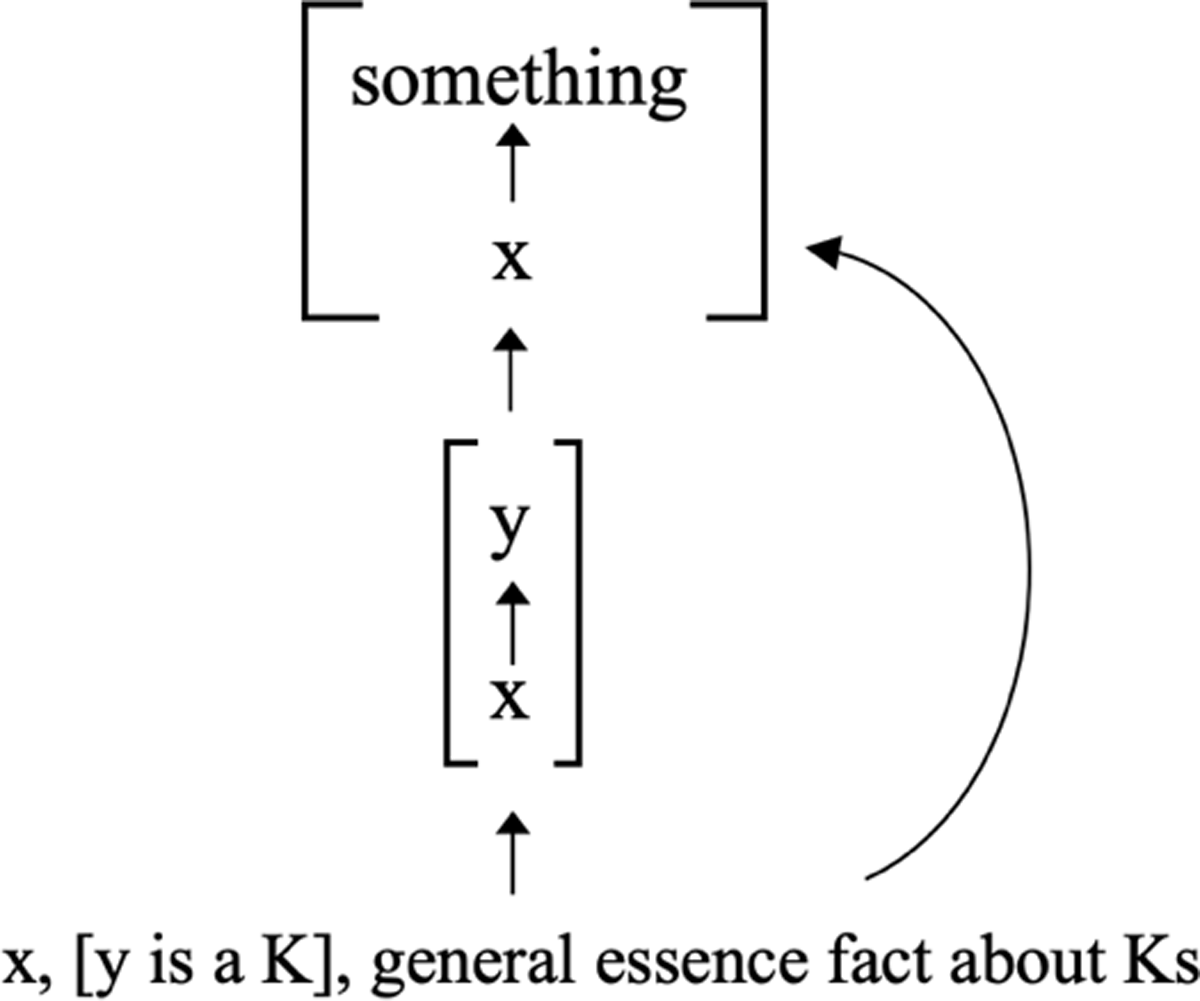
The most popular answer to the question of what grounds the grounding facts, which I shall call Bottom-up Particularism, was first proposed and defended by Karen Bennett (2011b) and Louis deRosset (2013).8 Suppose that Socrates (either partially or fully) grounds {Socrates}. According to Bottom-up Particularism, the grounding fact [Socrates grounds {Socrates}] is itself fully grounded in the particular entity at the “bottom” of the grounding fact—in this case, Socrates.
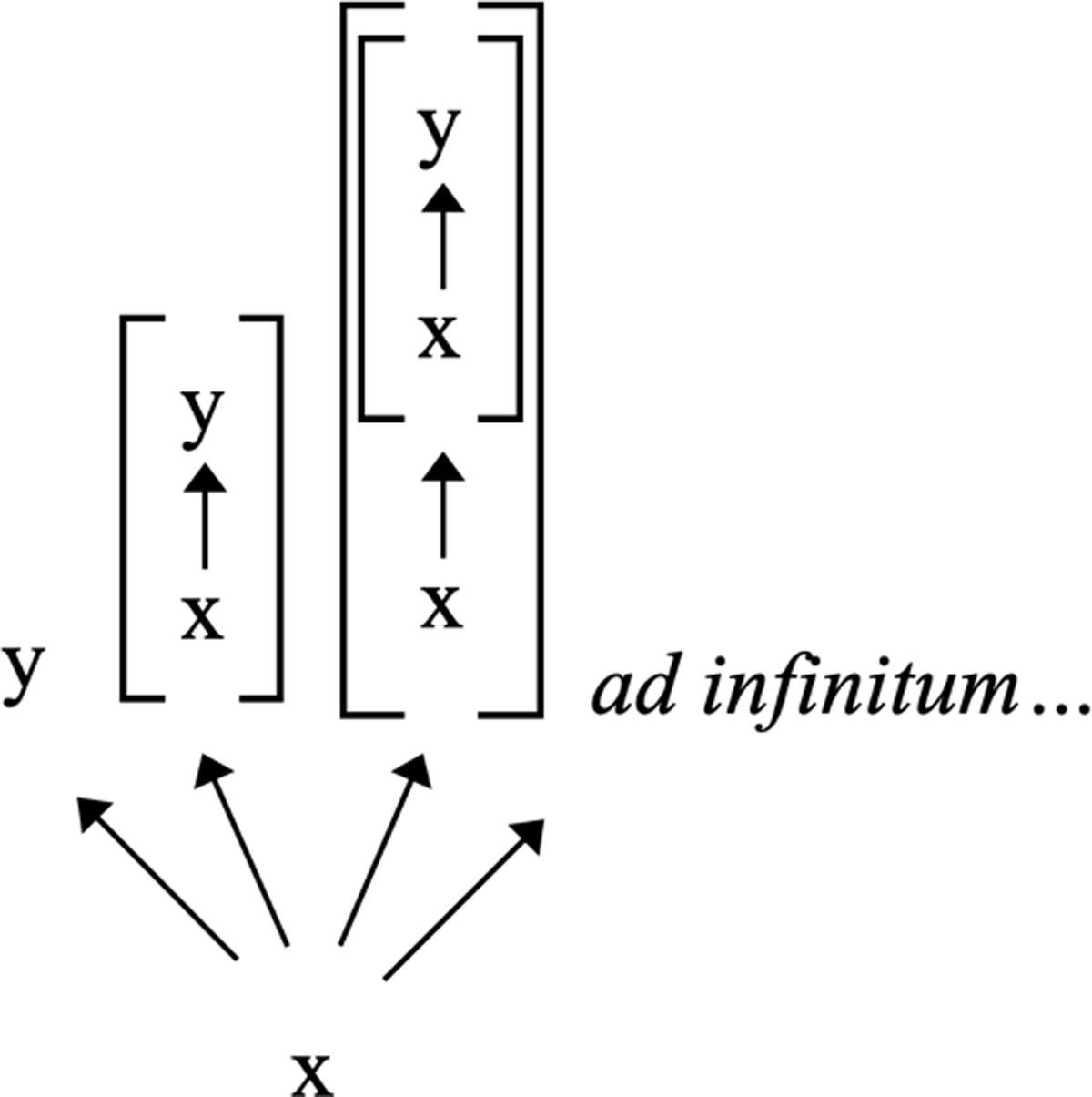
More generally, according to Bottom-up Particularism, for any x and y, if x (either partially or fully) grounds y, then [x grounds y] is itself fully grounded in x. Bottom-up Particularism thus generates a second-order grounding fact, namely: [x fully grounds [x grounds y]]. What fully grounds that grounding fact? Bottom-Up Particularism answers—x fully grounds [x fully grounds [x grounds y]]. Indeed, x fully grounds the third-order grounding fact [x fully grounds [x fully grounds [x grounds y]]]. And so on, ad infinitum.9
Figure 1 represents the resulting infinite regress of grounding facts. The square brackets represent facts, the letters represent constituents of those facts, and the arrows represent the relation of full grounding:
Figure 1 also reveals that grounded entity y has groundmates. For instance, [x grounds y] is numerically distinct from grounded entity y. Yet both are fully grounded in x. So [x grounds y] is grounded entity y’s groundmate.10 The second-order grounding fact [x fully grounds [x grounds y]] is also one of entity y’s groundmates. Indeed, each and every one of the higher-order grounding facts in the infinite regress is one of entity y’s groundmates. Thus, if Bottom-Up Particularism is true, then every grounding fact has infinitely many distinct grounding facts as groundmates.11 I conclude that, if Bottom-Up Particularism is true, then our arbitrarily chosen grounding fact has groundmates.
2.2. Top-Down Particularism
Consider some entity a that either partially or fully grounds entity b. Then there is at least one grounding fact, namely, [a grounds b]. According to Top-down Particularism, [a grounds b] is itself fully grounded in the nature of the entity at the “top” of the grounding fact, entity b. More generally, every grounding fact is fully grounded in the nature of the grounded entity at the top of the grounding fact.
Kit Fine explains:
. . . [W]hat explains the ball’s being red or green in virtue of its being red is something about the nature of what it is for the ball to be red or green (and about the nature of disjunction in particular) and not something about the nature of what it is for the ball to be red. It is the fact to be grounded that ‘points’ to its ground and not the grounds that point to what they may ground. . . . Thus the asymmetry supports a top-down approach in which we start with the facts to be grounded and work our way down to their grounds, rather than the other way around. (2012: 76.)
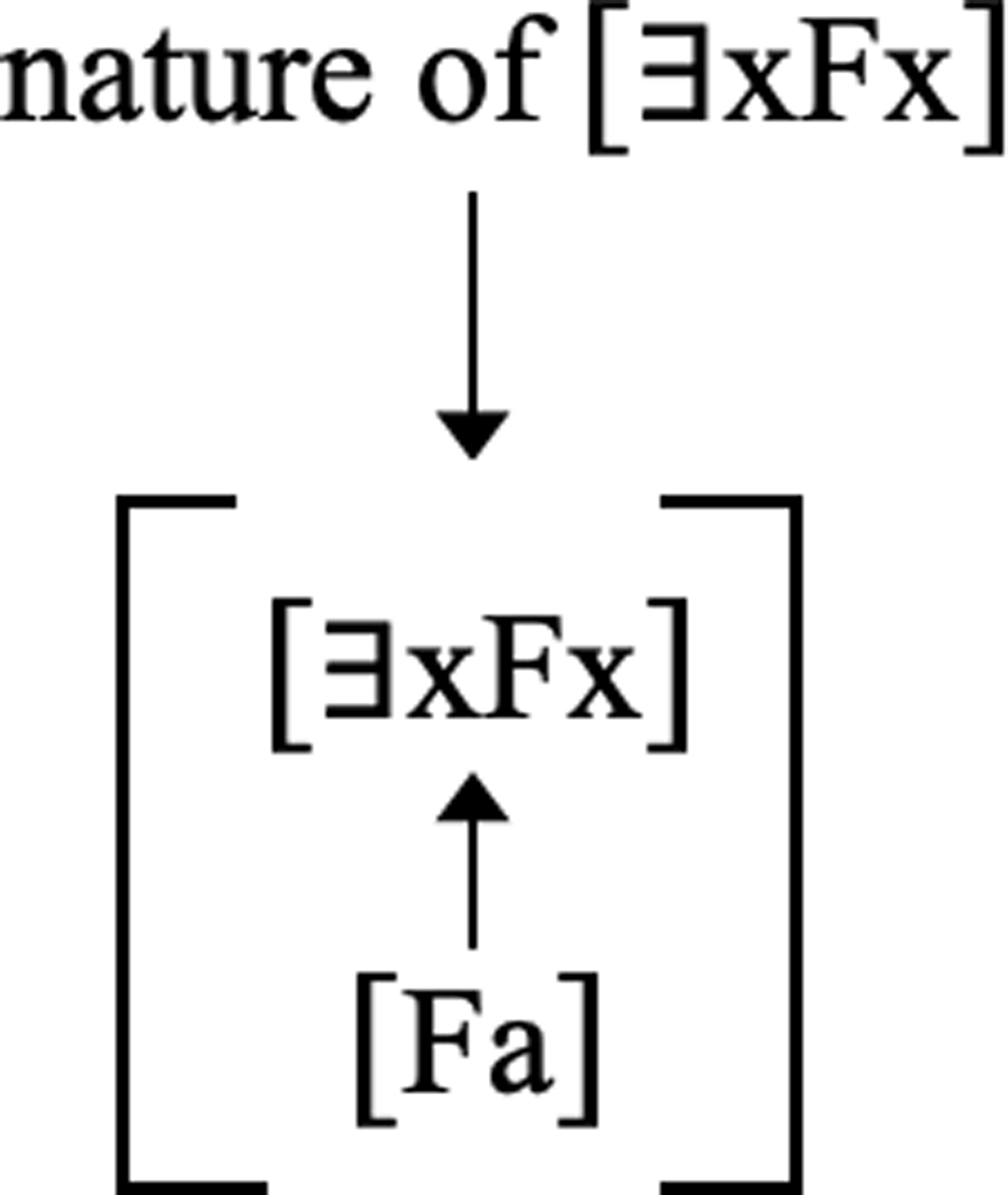
Fine goes on to give a more detailed example involving the grounds of existentially quantified facts (2012: 75).12 Fine assumes, as is standard, that existentially quantified facts are grounded in their instances. For example, if entity a is F, then the existentially quantified fact [∃xFx] is grounded in [Fa]. According to Fine, the resulting grounding fact, [[Fa] grounds [∃xFx]], is itself fully grounded in a fact about what lies in the nature of [∃xFx]. Specifically, [[Fa] grounds [∃xFx]] is fully grounded in [it lies in the nature of [∃xFx] that, for any x, if x is F, then the fact that x is F grounds [∃xFx]].
Figure 2 depicts the grounding of [[Fa] grounds [∃xFx]]:
However, as Figure 2 makes clear, the grounding of [[Fa] grounds [∃xFx]] in the nature of [∃xFx] generates a second-order grounding fact, namely, the fact that the relevant fact about what lies in the nature of [∃xFx] grounds [[Fa] grounds [∃xFx]]. And this second-order grounding fact, no less than the original first-order grounding fact, requires a ground.
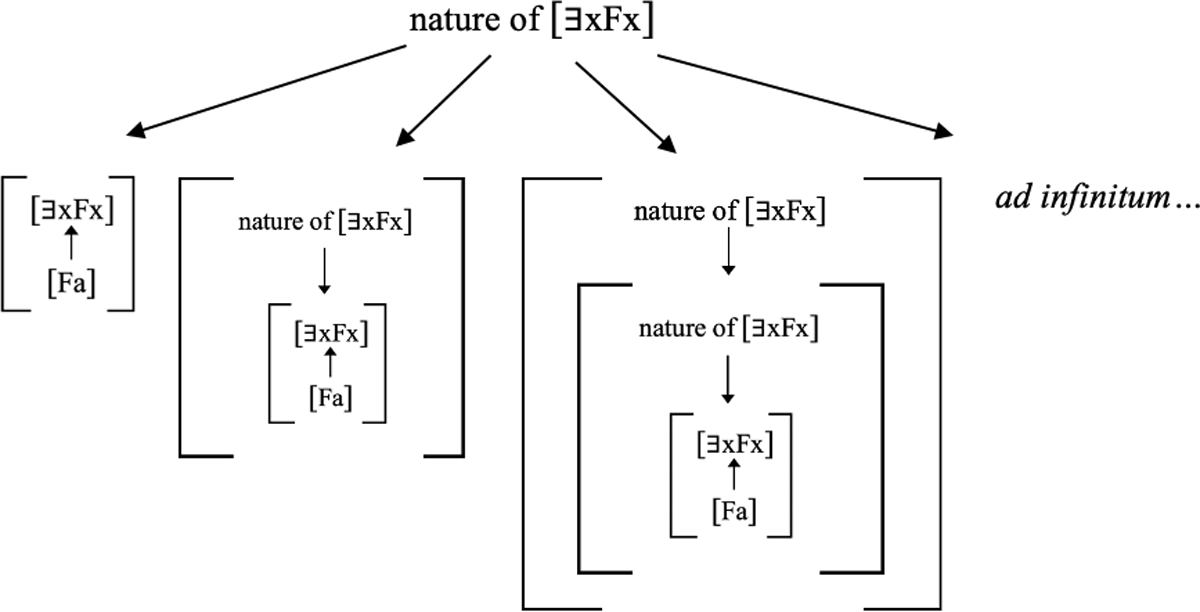
At the second-order level and beyond, the Top-Down Particularist can take an approach that is the mirror-image of the Bottom-Up Particularism—the very same fact about the nature of the original “top” entity, in this case [∃xFx], serves as the full ground of the new second-order grounding fact as well. Indeed, that same fact about the nature of [∃xFx] can serve as the full grounds of the third-order grounding fact, the fourth-order grounding fact, and so on at each of the infinitely many new iterated levels of grounding facts. On this view, then, the entire hierarchy of grounding facts billows downward from above, rather than blooming upwards from below.
Figure 3 depicts the result:
As Figure 3 makes clear, Top-Down Particularism entails that some grounded entities have groundmates. For example, the first-order grounding fact [[Fa] grounds [∃xFx]] has the second-order grounding fact [[its lying in the nature of [∃xFx] that, for any x, if x is F then [Fx] grounds [∃xFx]] fully grounds [[Fa] grounds [∃xFx]]]. For those two grounding facts are numerically distinct—one has a nature fact among its constituents, while the other does not. Nevertheless, they are both fully grounded in the same fact about what lies in the nature of [∃xFx]. Indeed, the first-order grounding fact [[Fa] grounds [∃xFx]] has infinitely many other higher-order grounding facts among its groundmates.
2.3. An Assumption
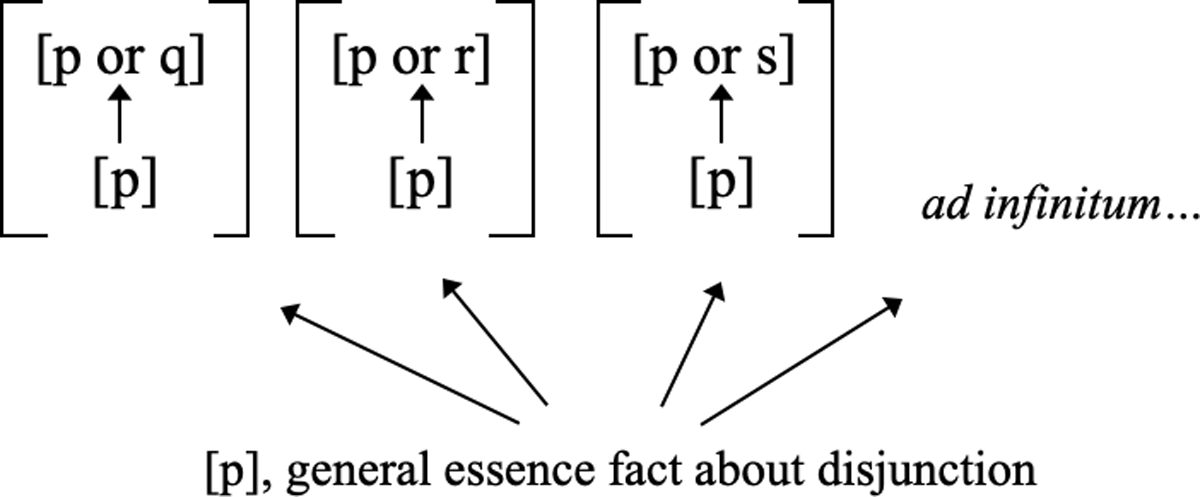
Suppose that [p] exists. According to the orthodoxy, if there are disjunctive facts, then they are fully grounded in their true disjunct(s) (cf. Rosen 2010: 117). For example, if there are disjunctive facts, then [p or q] is fully grounded in [p]. Indeed, if there are disjunctive facts, then there are infinitely many disjunctive facts fully grounded in [p]—ex. [p or r], [p or s], [p or t], and so on ad infinitum.
Notice that every one of the infinitely many disjunctive facts is numerically distinct from each of the other disjunctive facts. After all, no two of these facts have precisely the same constituents. Nevertheless, they share at least one full ground, namely, [p]. Thus, every one of the disjunctive facts in the series [p or q], [p or r], [p or s], [p or t], and so on, has each of the other disjunctive facts in that series as its groundmate. Therefore, if there are disjunctive facts, then there are groundmates.
Suppose there is at least one grounded entity b, and that b is fully grounded in some distinct entity a. Then the grounding fact [a fully grounds b] exists. According to the orthodoxy, if there are existentially quantified facts, then they are fully grounded in their true instances (cf. Correia & Schneider 2012: 18 and Fine 2010: 101). For example, if there are existentially quantified facts, then the existentially quantified fact [a fully grounds something] is fully grounded in [a fully grounds b]. Moreover, if there are existentially quantified facts, then the existentially quantified fact [something fully grounds something] is fully grounded in [a fully grounds something].
As a result, if there are existentially quantified facts, then there are chains of full grounding involving those facts. For example, [a fully grounds b] fully grounds the existentially quantified fact [a fully grounds something], which in turn fully grounds another existentially quantified fact [something fully grounds something]. Full grounding is transitive. Thus, [a fully grounds b] fully grounds both [a fully grounds something] and [something fully grounds something]. Those latter two facts are numerically distinct from one another. Yet they are both fully grounded in [a fully grounds b]. So they are one another’s groundmates. Therefore, if there are existentially quantified facts, then there are groundmates.
The arguments of §2.4–6 will draw upon the following modest first-order assumption: either there are disjunctive facts or there are existentially quantified facts. I shall argue that the two other accounts of what grounds the grounding facts, when conjoined with this modest first-order assumption, imply that every grounding fact has either a disjunctive fact or an existentially quantified fact (or both) among its groundmates.
2.4. Simple Generalism
According to Simple Generalism, for any x and y, if x grounds y, then [x grounds y] is partially grounded in the bottom entity, entity x.13 But entity x is not the full grounds of that grounding fact. In addition, Simple Generalism adds a general “connecting” principle linking x-type entities to y-type entities. Shamik Dasgupta, this view’s main proponent, explains:
. . . [C]onsider a particular philosophy conference, an event lasting a few days, and call the event e. Then, arguably, the fact that e is a conference is not brute, but holds in virtue of the fact that e contains people engaged in various conference-conducive activities (some are giving papers, others listen and ask questions, and so on). Call these kinds of activities “C-activities.” Then we have:
(F) The fact that e contains people engaged in C-activities grounds the fact that e is a conference.
. . . Our question is: What (if anything) grounds (F)? . . . A very natural answer has to do with the kind of thing that conferences are, in general. A conference is the kind of thing that you get when people engage in those activities; that is why, when those particular people in e engaged in them, the result was a conference. This is to ground (F) in a general connection between conferences and activities. (Dasgupta 2014: 566–68)
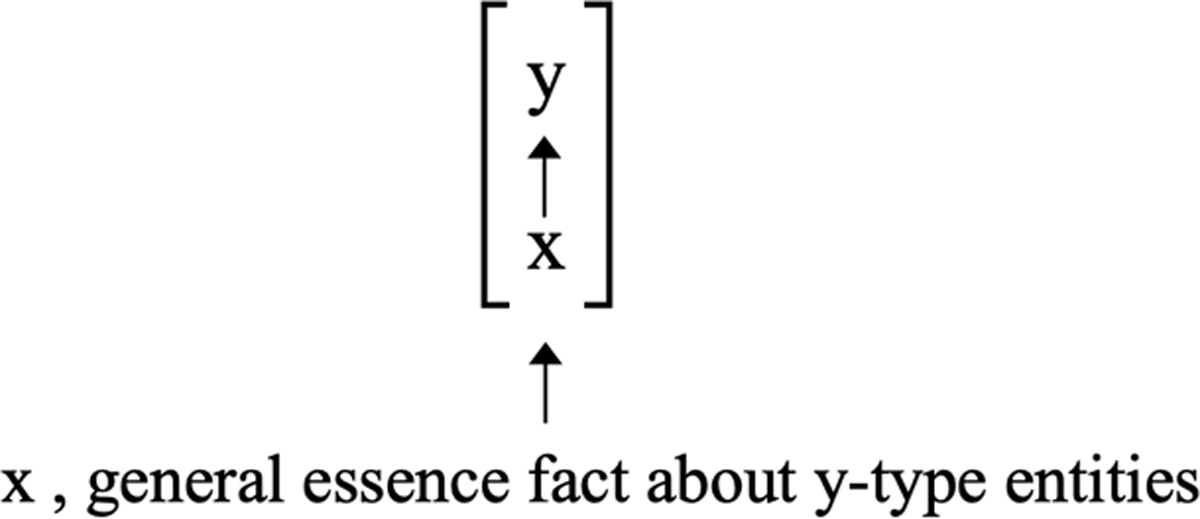
Thus, where entity x grounds entity y, the grounding fact [x grounds y] is partially grounded in entity x and partially grounded in a general principle connecting x-type entities to y-type entities. Entity x and that general principle, taken together, constitute the full grounds of the grounding fact [x grounds y].
Figure 4 depicts Simple Generalism’s account of what fully grounds [x grounds y]:
What are these general connective principles that help ground the grounding facts? Dasgupta identifies these general principles with essence facts—specifically, facts about the essence of the kind to which the entity at the “top” of the grounding fact belongs.14 For example, consider the grounding fact [Socrates grounds {Socrates}]. That grounding fact is fully grounded in Socrates together with a general essence fact about sets. That general essence fact might look something like this: [it is essential to being a set that, for any set S, if the xs are members of S, then S is grounded in the xs].15
According to Dasgupta, the general essence facts are ungrounded. Nevertheless, they are not fundamental. Dasgupta distinguishes between substantive facts, which are “apt” for being grounded, and autonomous facts, which are “inapt” for grounding. The fundamental facts, if there are any, are all and only those ungrounded facts that are also substantive. A fact that is ungrounded but autonomous, by contrast, is neither fundamental nor derivative. The general essence facts fall into this latter category. So, even though the general essence facts are ungrounded and contain derivative entities as constituents, they do not violate Purity (see Dasgupta 2014: 575; 2016: 383).
My argument for the claim that Simple Generalism leads to groundmates assumes that there are disjunctive facts (§2.3). That assumption, when conjoined with Simple Generalism, generates groundmates for every grounding fact.
Suppose that there are disjunctive facts. Suppose that some fact [p] exists. The disjunctive fact [p or q] is grounded in [p] (see §2.3). Of course, [p or r] is also grounded in [p]. As a result, we have two numerically distinct grounding facts on our hands—[[p] grounds [p or q]], and [[p] grounds [p or r]]. According to Simple Generalism, each of these grounding facts is fully grounded in some other fact(s). Let us take each in turn.
The grounding fact [[p] grounds [p or q]] is fully grounded in the “bottom” entity, [p], together with a general essence fact about the sort of entity at the “top,” such as the following: [it is essential to disjunction that every disjunctive fact is grounded in its true disjunct(s)]. Now consider [[p] grounds [p or r]]. This grounding fact has the same “bottom” entity, [p]. Moreover, the “top” entity is a disjunctive fact. As a result, the very same two entities—[p] and the general essence fact about disjunction—also serve as the full grounds for the grounding fact [[p] grounds [p or r]].
Indeed, there are infinitely many facts about what grounds the disjunctive facts with [p] as a true disjunct—[[p] grounds [p or s]], [[p] grounds [p or t]], [[p] grounds [p or u]], and so on ad infintum. And, in each case, Simple Generalism assigns the same full grounds, that is, [p] and the same general essence fact about disjunction. Figure 5 depicts the result:
As Figure 5 makes clear, [[p] grounds [p or q]] has another grounding fact, [[p] grounds [p or r]] as its groundmate. For the former is numerically distinct from the latter. Yet there are some facts that fully ground them both. Indeed, each and every grounding fact has infinitely many distinct grounding facts as groundmates.
2.5. Complex Generalism
Complex Generalism says that, where x grounds y, the grounding fact [x grounds y] is itself partially grounded in x and partially grounded in a general principle connecting x-type entities to y-type entities. However, unlike Simple Generalism, Complex Generalism adds a third partial ground, namely, the particular entity at “top” of the original grounding fact, entity y.
Gideon Rosen is Complex Generalism’s only advocate (see Rosen 2010: §13). Rosen’s illustration of Complex Generalism draws on a first-order assumption about what grounds what. Specifically, Rosen assumes that disjunctive facts of the form [p or q] are grounded in their true disjuncts. Following Rosen, then, let us assume that some fact p is true, and that the disjunctive fact, [p or q], is grounded in [p]. What grounds [[p] grounds [p or q]]? Rosen explains:
The disjunctive fact [p ∨ q] is grounded in [p]. Why? Let’s make the explanation as explicit as possible. [p ∨ q] is grounded in [p] because:
- (a)
P is true
- (b)
[p ∨ q] is a disjunctive fact with p as one of its disjuncts
- (c)
In general, if p is true, then [p ∨ q] is grounded in [p].
And why is (c) true? Because:
- (d)
It lies in the essence of disjunction that, for all p, q: (if p is true, then [p ∨ q] is grounded in [p]). (Rosen 2010: 130)
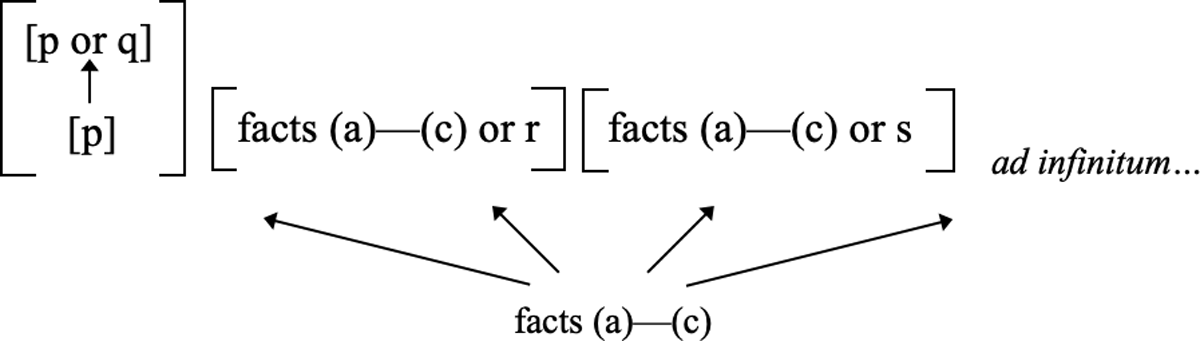
Thus, the grounding fact [[p] grounds [p or q]] is fully grounded in the following facts, taken together: (a) the “bottom” fact, [p], (b) the fact that the “top” fact [p or q] is a disjunctive fact that has [p] as a disjunct; and then, ultimately, (c) a general fact about the essence of disjunction. Let “Facts (a)–(c)” be a plural referring expression that picks out facts (a), (b), and (c), collectively.
Suppose [[p] grounds [p or q]] is indeed fully grounded in Facts (a)–(c). Now consider the following disjunctive fact: [Facts (a)–(c) or [r]]. That disjunctive fact has Facts (a)–(c) as a true disjunct. We are assuming that disjunctive facts are fully grounded in their true disjuncts. Hence, the disjunctive fact [Facts (a)–(c) or [r]] is fully grounded in Facts (a)–(c).
So Facts (a)–(c) are doing double-duty—they jointly serve as the full grounds for [[p] grounds [p or q]] and they jointly serve as the full grounds for the disjunctive fact [Facts (a)–(c) or [r]]. Of course, the former fact is distinct from the latter fact. So the grounding fact [[p] grounds [p or q]] shares its full grounds with a numerically distinct grounded entity.
Figure 6 depicts the resulting grounding structure:
As Figure 6 makes clear, the grounding fact [[p] grounds [p or q]] has a disjunctive fact as its groundmate. Indeed, it has infinitely many disjunctive facts as its groundmates.
There is another route from Complex Generalism to groundmates that does not presuppose that there are disjunctive facts. Instead, the second route relies on the assumption that there are existentially quantified facts (§2.3). That assumption, when conjoined with Complex Generalism, generates groundmates for every grounding fact.
Suppose there is one grounded entity, entity y, which is grounded in entity x. Then the following grounding fact obtains: [x grounds y]. Now consider the existentially quantified fact [x grounds something]. The grounding fact [x grounds y] is an instance of [x grounds something]. Existentially quantified facts are fully grounded in their instances (§2.3). So the existentially quantified fact [x grounds something] is fully grounded in the grounding fact [x grounds y].
Now add to this that Complex Generalism’s account of what grounds the grounding facts is true. Then the grounding fact [x grounds y] is itself fully grounded in entity x, [entity y belongs to kind K], and a general essence fact about K, taken together.
We now have a chain of full grounding—the existentially quantified fact [x grounds something] is fully grounded in the grounding fact [x grounds y], which in turn is fully grounded in entity x, [entity y belongs to kind K], and a general essence fact about Ks, taken together. Full grounding is transitive. Thus, the latter three facts fully ground the existentially quantified fact [x grounds something]. As a result, those three facts fully ground both a grounding fact and an existentially quantified fact.
As Figure 7 makes clear, the grounding fact [x grounds y] has the existentially quantified fact [x grounds something] as its groundmate. For the two facts are numerically distinct. Yet they share one of their full grounds.
2.6. A General Defense
I have argued that each individual account of what grounds the grounding facts generates groundmates (§2.1–5) I shall close this section by arguing that if GGT is true then, whatever account of what grounds the grounding facts turns out to be correct, some grounded entity has a groundmate.
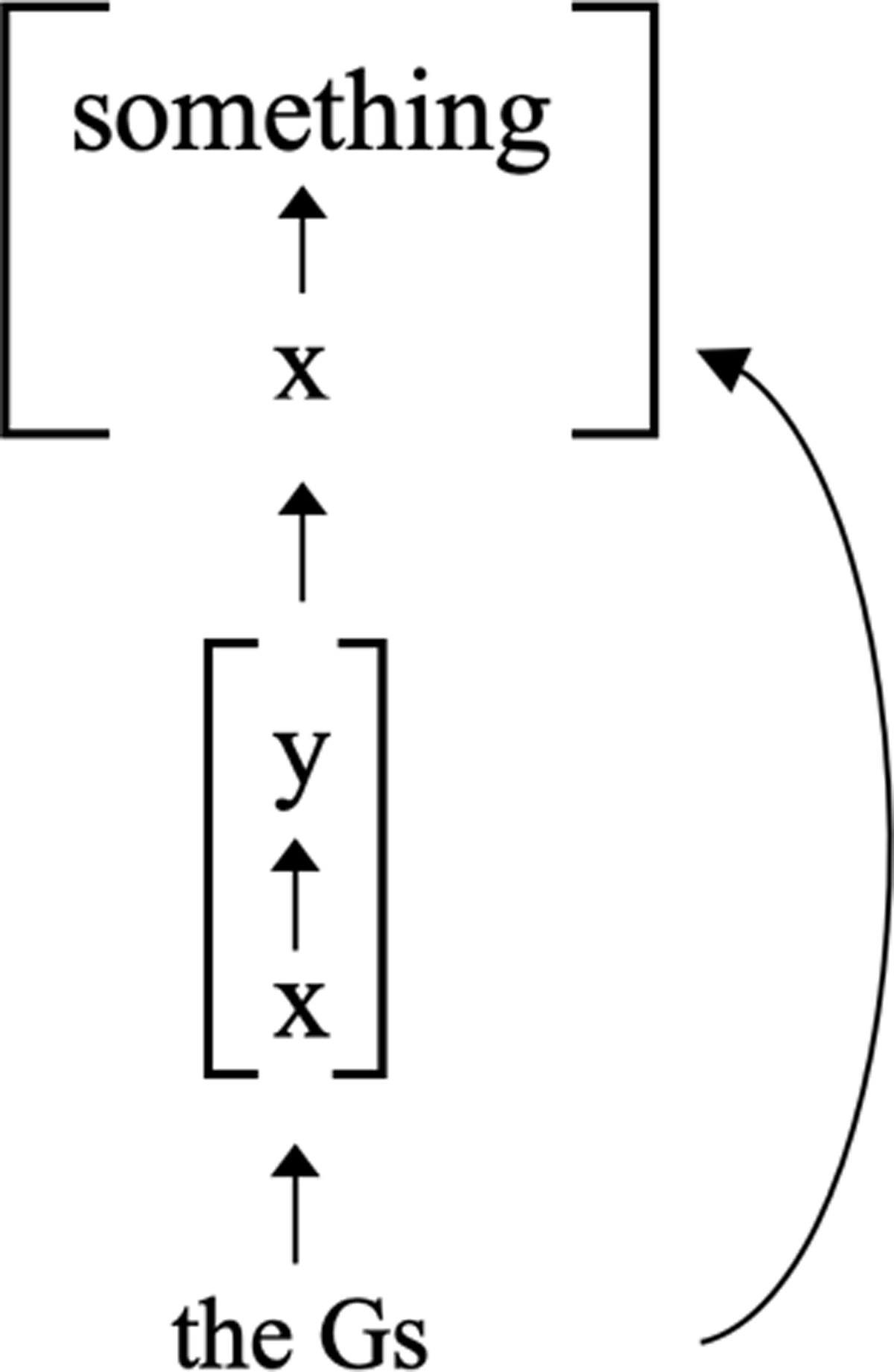
Suppose GGT is true. And suppose that x grounds y. Then the grounding fact [x grounds y], like every other grounding fact, is itself fully grounded. Let “the Gs” be that entity or those entities, whatever they are, that jointly fully ground [x grounds y]. Perhaps one of the above four views gives the correct account of the Gs. Or perhaps none of them is correct and the Gs are something else entirely. The only thing that matters is that the Gs, whatever they are, fully ground the grounding fact [x grounds y].
Consider the existentially quantified fact [x grounds something]. The fact [x grounds something] is fully grounded in each of its instances. The grounding fact [x grounds y] is an instance of the existentially quantified fact [x grounds something]. Therefore, [x grounds something] is itself fully grounded in [x grounds y].
So [x grounds something] is fully grounded in [x grounds y], and [x grounds y] is fully grounded in the Gs. Full grounding is transitive. It follows that [x grounds something] is fully grounded in the Gs. Of course, [x grounds something] is numerically distinct from [x grounds y]. Therefore, the Gs fully ground two, numerically distinct facts—both [x grounds y] and [x grounds something].
This situation is illustrated in Figure 8 below:
As Figure 8 makes clear, [x grounds y] and [x grounds something] are groundmates Therefore, if there are existentially quantified facts, then GGT’s truth implies the existence of groundmates.
3. Purity and Groundmates
Let us say that any fact of the form [x is φ] is a groundmate differentiating fact (or GMD fact) just in case the following conditions are all met: (i) x is a grounded entity, (ii) x has property φ, (iii) there is some distinct grounded entity y that is x’s groundmate, and (iv) entity y does not have property φ.16
For example, suppose the set {Socrates} and the existential fact [Socrates exists] are groundmates—they are numerically distinct, but both are fully grounded in Socrates. Then [{Socrates} is a set] is a GMD fact about {Socrates}. For {Socrates} has the property being a set, but [Socrates exists] does not have that property. By contrast, [{Socrates} is fully grounded in Socrates] is not a GMD fact about {Socrates}. For {Socrates} and [Socrates exists] both have the property being fully grounded in Socrates.
Here is Premise 4:
-
(4)
If Purity is true, then there are no groundmates.
I shall defend Premise 4 by arguing for its contrapositive:
-
(4*)
If there are groundmates, then Purity is false.
My argument for 4* proceeds via conditional proof. So I shall begin by assuming that some arbitrary grounded entity has a groundmate, and then show that Purity’s falsity follows from that assumption.17
Assume that there is some arbitrary grounded entity a. Also assume that there is some grounded entity b such that b is grounded entity a’s groundmate. By definition, grounded entities a and b are numerically distinct. Therefore, there must be at least one property F such that either a is F and b is not F or vice-versa.18 As a result, there is at least one GMD fact about grounded entity a, namely: [a is F].19
Now consider [a is F]. There are only two options with respect to [a is F]—either that fact is fundamental, or else there are some facts, the Γs, such that the Γs fully ground [a is F]. Either way, it follows that Purity is false. Let us look at each option in turn.
On the one hand, suppose that [a is F] is fundamental. Of course, [a is F] has grounded entity a as a constituent. So there is at least one fundamental fact that has a grounded entity as a constituent. Therefore, Purity is false.
On the other hand, suppose that [a is F] is fully grounded in some other facts, the Γs. What sorts of facts are among the Γs? Well, we can be certain that there is at least one other GMD fact about grounded entity a among the Γs. To begin to see why, let us suppose that grounded entity a has property G. Moreover, let us furthermore assume that [a is F] is fully grounded in [a is G] alone.
Now assume—for purposes of reductio—that [a is G] is not a GMD fact about grounded entity a. This assumption leads to a contradiction. For any grounded entity x, if y is x’s groundmate then if y is not φ and x is φ then [x is φ] is a GMD fact about x. We are assuming that [a is G] is not a GMD fact about grounded entity a. It follows that a’s groundmate, entity b, must also be G. And, since b is G, b must be F as well. For a’s being G serves as the full grounds for a’s being F. In general, then, any x that is G is also F. Hence, b is F. Yet we are also assuming that [a is F] is a GMD fact about grounded entity a. By definition, then, b cannot be F. Therefore, b is F and b is not F. Contradiction. So, contra what was assumed for reductio, [a is G] is indeed a GMD fact about grounded entity a.
I have just argued there must be at least one other GMD fact about grounded entity a about the full grounds of [a is F]. Of course, there is nothing special about [a is F]. I could have used the same line of reasoning, mutatis mutandis, to show that any GMD fact about grounded entity a must have at least one other GMD fact about grounded entity a among its full grounds (if, that is, the former is grounded rather than fundamental). So I conclude that every GMD fact that is grounded has at least one other GMD fact among its full grounds.
Now return to the full grounds of [a is F], the GMD fact [a is G]. Either [a is G] is fundamental or else there are some further fact(s) that serve to fully ground [a is G]. If the former, then Purity is false. If the latter, then there must be some third GMD fact about grounded entity a, [a is H], which is among the full grounds of [a is G]. For every GMD fact must have at least one other GMD fact among its full grounds.20
Of course, the same two options arise with respect to this new GMD fact—either [a is H] is absolutely fundamental or else there are some facts that fully ground it. If the former, then Purity is false. If the latter, then there is yet another GMD fact about grounded entity a among the full grounds of [a is H]. And so on.
Let the GMD series be the resulting series of increasingly fundamental GMD facts about grounded entity a—the series that begins with GMD facts [a is F], [a is G], and [a is H]. Following Dixon (2016) and Rabin and Rabern (2016), I shall assume that the following weak version of metaphysical foundationalism governs every chain of full grounding:
Weak Foundationalism (WF): for any derivative entity x, there are some fundamental entities, the ys, such that the ys are the ultimate full grounds of x (see Dixon 2016: 466; also see Rabin & Rabern 2016).
Every grounded entity is derivative. So WF implies that every grounded entity is ultimately fully grounded in some fundamental entity or entities.21
Of course, every fact in the GMD series is a grounded entity. So, given WF, for every fact in the GMD series, there is some absolutely fundamental entity or entities that serve as its ultimate full grounds. Every fact in the GMD series is a GMD fact. And there must be at least one GMD fact among the full grounds of any GMD fact that has a ground. It follows that every fact in the GMD series is fully grounded in some fact(s) that is both fundamental and a GMD fact about grounded entity a.
Figure 9 depicts the two possible grounding structures that are consistent with WF:
The lefthand grounding structure is an infinitely descending chain of non-fundamental GMD facts about grounded entity a, which of which is (i) fully grounded by another non-fundamental GMD fact in the chain, and (ii) fully grounded by an absolutely fundamental GMD fact about grounded entity a. The righthand grounding structure is a finite chain of non-fundamental GMD facts about grounded entity a, which ultimately terminates in an absolutely fundamental GMD fact about grounded entity a. Either way, there is at least one fundamental GMD fact about grounded entity a.
I just argued that there is at least one fundamental GMD fact about grounded entity a. We do not know much about the identity of that fact. But we do know that it is a GMD fact about grounded entity a. As a result, we know that it contains grounded entity a as a constituent. So we know that it contains a grounded entity as a constituent. Yet it is a fundamental fact. Therefore, there is at least one fundamental fact with a grounded constituent. Purity is false.
4. Grounding Ungrounded
Again, this paper’s main conclusion is that Purity is false. That is an important conclusion in its own right. But Purity’s demise spells trouble for a second grounding piety, namely, the Grounding Grounding Thesis. For starters, the falsity of Purity renders GGT completely unmotivated. There are two ways to see this.
First, recall that GGT’s most prominent defenders generally cite Purity as the main reason to think that every grounding fact has a ground (see §1).22 So this paper’s first conclusion, that Purity is false, undercuts main extant argument for GGT.
Second, there is a more substantive way to see that the falsity of Purity leaves GGT unmotivated. Suppose that Purity is false, that is, that there is some fundamental fact containing a derivative or grounded entity as a constituent. For example, suppose that a fully grounds b. And suppose you know that the following is a fundamental fact about derivative entity b: [b is F].
Now consider a different fact about derivative entity b: [b is G]. Imagine you are asked, based only on what you know so far, whether [b is G] is itself a fundamental fact. Clearly it would be unmotivated of you to insist, without any further argument, that [b is G] is a derivative rather than fundamental fact. After all, you know that at least one other fact about entity b, [b is F] is a fundamental fact. In the absence of any further argument, you should simply withhold judgment.
More generally, once you learn that there is at least one fundamental fact containing derivative entity b as a constituent, you cannot simply assume every single fact about entity b is going to be derivative rather than fundamental. For any fact about derivative entity b, in the absence of further argument, you should simply withhold judgment about that fact’s status as fundamental or derivative.
Now consider another fact containing derivative entity b as a constituent: [a grounds b]. Imagine you are asked whether this fact is fundamental or derivative. Just as before, it would be unmotivated of you to insist, without any further argument, that [a grounds b] is itself a derivative fact. After all, you know that there is at least one other fact about entity b, [b is F] that is fundamental. In the absence of a further argument, you should simply withhold judgment.
Of course, you might come across a good reason to think that some fact about derivative entity y is itself derivative rather than fundamental. For example, consider the conjunctive fact [b is F and c is H]. And suppose you have good reason to think that, in general, conjunctive facts are grounded in their conjuncts. This would give you reason to think that every conjunctive fact, including [b is F and c is H], is derivative. It is motivated for you to conclude that [b is F and c is H], though, only insofar as you have some further reason for thinking that every conjunctive fact is derivative.
If Purity is false, then there are some fundamental facts containing derivative entities as constituents. Grounding facts, facts about what grounds what, contain derivative entities as constituents. So, if Purity is false, it would be unmotivated of us to insist that no grounding fact is fundamental. That is, it would be unmotivated to insist that each and every grounding fact is itself grounded. Thus, if Purity is false then accepting GGT is unmotivated.
At the very least, we should be agnostic about the truth of any unmotivated philosophical thesis. So, at the very least, we should be agnostic about the truth of GGT. However, we sometimes have good reason to reject an unmotivated philosophical thesis. And GGT is one such unmotivated thesis. Or so I shall argue below.
Let us begin by considering a different, but equally unmotivated, philosophical thesis—Homuncular Dualism. Homuncular Dualism (HD) is the conjunction of two theses. First, a person S is consciously thinking that p just in case there is some distinct, smaller person S* inside S’s head who is thinking that S is thinking that p. Second, every conscious mental fact—every fact of the form [S is in conscious mental state M]—is a fundamental fact.
I assume that you, like me, reject HD. You probably have many reasons for rejecting HD. For example, you probably know that it is empirically false that people have other, smaller people living inside their heads. Perhaps you also endorse some form of physicalism about the mental, and therefore have reason to reject HD’s claim that every conscious mental fact is a fundamental fact. However, even if you were neither a physicalist nor empirically informed, you would still have sufficient reason to reject HD.
To see this, first note that the truth of HD immediately leads to an infinite regress. Suppose that person x is thinking that p. HD says that inside the head of every person x thinking that p there is a distinct homuncular person thinking that x is thinking that p. Thus, there is some homunculus y that is thinking that person x is thinking that p. Moreover, there is yet another homunculus z inside homunculus y’s head, thinking that homunculus y is thinking that person x is thinking that p. And so on, ad infinitum.
Next note that HD’s infinite regress of ever smaller homunculi is accompanied by another regress of infinitely many fundamental facts. First, there is the fundamental fact that person S is thinking that p. Second, there is the fundamental fact that homunculus S* is thinking that S is thinking that p. Third, there is the fundamental fact that homunculus S** is thinking that homunculus S* is thinking that S is thinking that p. And so on, ad infinitum.
So HD’s truth entails that there are infinitely many fundamental facts. Moreover, HD is completely unmotivated—you have no good reason to believe it. As a result, I think it would be epistemically irresponsible of you to merely remain agnostic about HD’s truth. Instead, you have good reason to regard HD as false.
More generally, I think you should regard as false any completely unmotivated philosophical thesis whose truth implies the existence of infinitely many fundamental facts (see Barker 2021). That is, I endorse the following principle:
Principle: for any philosophical thesis T, we should reject T if (1) we have no good reason to believe that T is true and (2) if T’s truth would imply the existence of infinitely many new fundamental facts.
My argument against the Grounding Grounding Thesis, like my argument against HD, relies on the truth of Principle. Before getting to that argument, though, I want to note what Principle does not say.
Principle does not say that we should reject any philosophical thesis whose truth implies the existence of an infinite regress of facts. For example, consider the T-schema, according to which p if and only if it is true that p. It is well-known that the T-schema implies infinitely many facts. Suppose that p. Thus, assuming the T-schema, it is true that p. Thus, it is true that it is true that p. Thus, it is true that it is true that it is true that p. And so on, ad infinitum.
The truth of the T-schema leads to an infinite regress of facts. However, Principle does not instruct us to reject the T-schema. After all, the T-schema is not completely unmotivated. We have good reason to believe it. And Principle instructs us only to reject unmotivated theses whose truth would lead to an infinite regress of facts.23
As Karen Bennett has argued, GGT implies the existence of infinitely many, numerically distinct grounding facts (see 2011b: 30–31). To see this, consider the following grounding fact: [x grounds y]. If GGT is true, then [x grounds y] is itself grounded in something, z. Thus we have another grounding fact: [z grounds [x grounds y]]. And, if GGT is true, that latter grounding fact is also grounded in something, z*. Thus we have another grounding fact: [z* grounds [z grounds [x grounds y]]]. And so on, ad infinitum.
Note that the infinite regress of grounding facts follows regardless of which specific account of what grounds the grounding facts is correct. After all, our starting assumption in the last paragraph was that [x grounds y] is grounded in something, z. For all I said, z could be the entity at the “bottom” of the grounding fact, x. Or it could be the entity at the “top” of the grounding fact. Or it could be the bottom entity together with a general connective principle. Regardless of what z is, the infinite regress of grounding facts follows.
Every defender of GGT recognizes that GGT implies an infinite regress of grounding facts. Nevertheless, GGT’s defenders are not generally bothered by this implication. For, as Bennett points out, each and every one of the infinitely many grounding facts in the regress is grounded rather than fundamental. And, she argues, while the postulation of infinitely many fundamental facts may be objectionable, the postulation of infinitely many new grounded facts is not objectionable (2011b: 32–35).24
Contra Bennett, however, the infinite regress of grounding facts is not harmless. To see this, first recall that, as I argued in Section 2.6, GGT’s truth entails that some grounded entity has a groundmate. My defense of that claim began by considering some arbitrary grounding fact, [x grounds y]. I then supposed that, per GGT, every grounding fact is grounded. If every grounding fact is grounded then, so I argued, the grounding fact [x grounds y] has a groundmate. I concluded that if GGT is true then some grounded entity has a groundmate.
But I chose the grounding fact [x grounds y] arbitrarily. So I now conclude that if GGT is true then every grounding fact has a groundmate. Moreover, as I argued in Section 3 above, there is a fundamental fact about every grounded entity with at least one groundmate. Therefore, I now conclude, if GGT is true then there is a fundamental fact about every grounding fact.
In light of this, return to the infinite regress of grounding fact generated by GGT. It is true that each of these infinitely many grounding facts, per GGT, is itself grounded rather than fundamental. However, if GGT is true then there is a fundamental fact about every grounding fact. Thus, for each grounding fact in the infinite regress, there is a fundamental fact about that grounding fact. Since there are infinitely many grounding facts, there also are infinitely many fundamental facts accompanying them.
Therefore, if GGT is true then there are infinitely many fundamental facts, one for each grounding fact in the infinite regress of grounding facts. We have already seen that GGT is unmotivated. And Principle instructs us to reject any philosophical thesis that is both (1) unmotivated and (2) whose truth implies the existence of infinitely many new fundamental facts. Thus Principle instructs us to reject GGT. So I conclude that the Grounding Grounding Thesis is false—some grounding facts are fundamental.
5. Fundamental Composition Grounding Facts
Which grounding facts are fundamental, and which are grounded? Using composition as a case study, I will close by arguing that traditional first-order metaphysics can and should play a role in the process of identifying the fundamental grounding facts.25
Conservatives about material objects believe that there are roughly all and only the composite material objects we ordinarily take there to be.26 For example, conservatives believe that there are such ordinary and familiar objects as living organisms, artifacts, and inanimate natural objects, but deny that there are extraordinary and unfamiliar objects like mereological sums of dogs and trees.
Consider Peter van Inwagen’s famous question about composition:
The Special Composition Question (SCQ): for any things, the xs, what non-mereological condition C is necessary and jointly sufficient for the xs to compose an object y? (see van Inwagen 1990)
An answer to SCQ provides a finite, non-disjunctive, and perfectly general condition C such that all and only those things that meet condition C compose a further object. For example, if any plurality of things whatsoever composes a further object, then there is an answer to SCQ—for any xs, the xs compose a y if and only if the xs are two or more in number.27
Let anti-criterialism about composition be the view that there is no true answer to SCQ. For example, suppose that, for any xs, the xs’ being such that their activities constitute a biological life is sufficient for their composing a further object. Also suppose that, for any xs, the xs’ being such that they are chemically bonded together suffices for their composing a further object. Finally, add that neither constituting a biological life nor being chemically bonded is a necessary condition for composition’s occurrence. Then there is no finite, non-disjunctive, and perfectly general condition C the meeting of which by any things whatsoever is necessary and sufficient for their composing a further object. So anti-criterialism is true.
Conservatives about material objects tend to be anti-criterialists.28 This is no accident. For conservatives believe in some spatially scattered objects, such as archipelagos and galaxies, but not others, such as dog-tree sums or archipelago-galaxy fusions. No one has been able to find a perfectly general, non-disjunctive condition that is met by all and only the putative parts of the conservative’s favored spatially scattered objects. After decades of searching, most conservatives are rightly pessimistic about the prospects of finding such an answer to SCQ.
Here is another question about composition:
Fundamental Composition Question (FCQ): for any xs, if the xs compose an object y, is [the xs compose y] fully grounded in some non-mereological fact(s), or is [the xs compose y] a fundamental fact?
SCQ asks whether there is some general condition that is both necessary and sufficient for composition’s occurrence. By contrast, FCQ asks whether the composition facts, under whatever conditions they occur, are grounded or fundamental.29
Let grounded composition be the view that every composition fact is grounded in the following sense—for any xs, if the xs compose a y, then [the xs compose y] is fully grounded in some non-mereological fact(s). Brutal composition, by contrast, is the view that, for any xs, if the xs compose a y, then [the xs compose y] is a fundamental fact.30
Anti-criterialism and grounded composition are consistent with one another. For suppose that some things, the ps, compose an object o1 and that [the ps compose o1] is fully grounded in [the activities of the ps constitute a biological life]. Add that some other things, the cs, compose a distinct object o2, and that [the cs compose o2] is fully grounded in [the cs are chemically bonded together]. Finally, add that there are no other composition facts. Then every composition fact is grounded. So grounded composition is true. Yet there is no general, non-disjunctive answer to SCQ. So anti-criterialism is also true.31
Moreover, conservatives should be attracted to the combination of anti-criterialism and grounded composition. We have already seen why they should accept anti-criterialism. As for grounded composition, note that conservatives tend to trust their intuitions. And, intuitively, whenever composition occurs, surely it does so because of or in virtue of something about the putative composing objects. Grounded composition vindicates this intuition. Brutalism about composition does not.32
The combination of grounded composition with anti-criterialism reveals a candidate fundamental grounding fact. Let the composition grounding facts be the facts about what grounds the composition facts. For example, suppose that [the ps compose o1] is fully grounded in [the ps are F]. Then [[the ps are F] fully grounds [the ps compose o1]] is a composition grounding fact. If there are composition grounding facts, then the question of what—if anything—grounds the composition grounding facts arises.
First, contra Bottom-Up Particularism, the conservative should deny that [the ps are F] fully grounds the first-order grounding fact [[the ps are F] fully grounds [the ps compose o1]], the second-order grounding fact [[the ps are F] fully grounds [[the ps are F] fully grounds [the ps compose o1]]], and so on ad infinitum. For, as I argued in Section 4, such infinite regress of grounding facts generates an unparsimonious infinite hierarchy of Purity-violating groundmates. Moreover, since Top-Down Particularism generates a mirror-image infinite regress, the conservative should not extend that account to the composition grounding facts either.
Second, contra both Simple and Complex Generalism, the conservative should deny that there is some general “connective” principle partly grounding [[the ps are F] fully grounds [the ps compose o1]]. For example, she should deny that there is a general essence fact about composition such as [it is essential to the composition relation that, for any xs, the xs compose y if and only if the xs are F] serving as a partial ground of the relevant composition grounding fact. She should also deny that there is an analogous law of metaphysics helping to partially ground the relevant composition grounding facts.
Indeed, the conservative must deny that there even is any such general connective principle! For any such general connective principle—whether it be in the form of a general essence fact, a law of metaphysics, or something else—would include a perfectly general, non-disjunctive necessary and sufficient condition for composition’s occurrence. However, according to anti-criterialism, there is no general and non-disjunctive condition that is both necessary and sufficient for composition’s occurrence. Conservatives, recall, should deny that any such general principle for composition exists. Therefore, conservatives should deny that any such general principle plays even a partial role in grounding the composition grounding facts.
The upshot, then, is that the conservative who embraces grounded composition and anti-criterialism should reject all four accounts of what grounds the grounding facts discussed in Section 2. I conclude that, if conservatism about composition is true, then the composition grounding facts are fundamental facts—although the composition facts are all fully grounded, nothing fully grounds the fact that the composition facts are grounded as they are.
Acknowledgements
I am grateful to Elizabeth Barnes, Ross Cameron, Jim Darcy, Dan Korman, Trenton Merricks, Noel Saenz, and Peter Tan for helpful feedback on the ideas in this paper. Trenton Merricks provided extensive feedback on multiple drafts of the dissertation chapter from which this paper is descended. Ross Cameron provided helpful feedback on Section 4, in particular. He also encouraged me to turn the dissertation chapter into a stand-alone article. Thanks to Rachel Barker for designing the diagrams. Finally, I am grateful to two anonymous referees at Ergo for multiple rounds of extensive and challenging feedback, which led to significant improvements in the paper’s structure and main line of argument.
Notes
- For a discussion of and an objection to Sider’s purity principle see Merricks (2013: 5–13). ⮭
- See Dasgupta (2014: §2) for his development of the “Siderean worry.” ⮭
- As we shall see, Dasgupta’s formulation of physicalism does permit ungrounded facts containing non-physical or derivative constituents. This is because Dasgupta argues that not all ungrounded facts are fundamental. For more details on Dasgupta’s view, see Section 2.3 below. ⮭
- Also see Michael Raven, who advocates the use of grounding to “purge” the non-fundamental from fundamental reality: “. . . A desirable application of ground [is] to purge the non-fundamental. The idea is that something can be purged from fundamental reality if the facts about it are grounded in facts not about it. Thus, we might wish to purge wars from fundamental reality by establishing that all facts about wars are grounded in facts not about wars” (2015: 328–29). Also see Raven (2016) for more on his “purging” requirement. Also see Bennett (2011b: 1). ⮭
- The only exception is Jon Litland (2017), who accepts Purity but denies that the grounding facts are grounded. But, it is worth noting, he also does not hold that the grounding facts are ungrounded. Instead, he argues that the grounding facts are “zero-grounded.” ⮭
- Versions of this argument from Purity to GGT are scattered throughout the literature. For influential early statements of the argument, see Bennett (2011a), Sider (2011), and deRosset (2013). ⮭
- No defender of Purity should deny the assumption that at least one entity has a ground. For that would be to deny that there are any grounded entities at all. However, if there are no grounded entities, then Purity is a mere vacuous truth. But presumably Purity’s defenders take that thesis to be a non-vacuous truth. After all, they offer arguments in its defense. So no defender of Purity should reject my first assumption. ⮭
- Korman (2015: 215–16) applies Bottom-Up Particularism to the so-called “grounding problem” for coincident objects. For discussion and criticism, see Dasgupta (2014) and Carnino (2016). ⮭
- Bennett (2011b) and deRosset (2013) both point out that Bottom-Up Particularism implies this infinitude of grounding facts, all fully grounded by the bottom entity. ⮭
- Figure 1 assumes that y fully grounds entity y. If y were a mere partial ground for grounded entity y, then grounded entity y and [x grounds y] would not be groundmates. However, [x grounds y] and [x fully grounds [x grounds y]] would be groundmates. So, even if y were a mere partial ground for entity y, Bottom-Up Particularism would still generate infinitely many groundmates. Similar remarks apply, mutatis mutandis, to Top-Down Particularism below. ⮭
- Saenz (2017) also points out that if Bottom-up Particularism is true, then multiple, distinct facts share their full grounds. ⮭
- Specifically, Fine gives the example of [[Socrates is a philosopher] grounds [someone is a philosopher]]. I am using the equivalent symbolic formulae to make higher-order grounding facts more tractable. ⮭
- Dasgupta (2014) calls his view the “connectivist” account of what grounds the grounding facts. ⮭
- Dasgupta and Sider both consider, but do not endorse, the view that the grounding facts are grounded in the “laws of metaphysics.” See Dasgupta (2014: 12) and Sider (2011: 145). For more on the laws of metaphysics, see Wasserman (2017), Wilsch (2015; 2016), Glazier (2016), Schaffer (2017a, 2017b), and Barker (2020). ⮭
- Dasgupta is officially agnostic between this formulation of the essence fact, which includes information about grounding, and a mere conditional formulation that does not include information about grounding. This does not matter for our purposes, however. See Dasgupta (2014: 568) for discussion. ⮭
- Many GMD facts about a given grounded entity are qualitative facts. But GMD facts need not be qualitative—if there are haeccaetistic facts about grounded entities with groundmates, then those haeccaetistic facts will be non-qualitative GMD facts about those grounded entities. Thanks to Ross Cameron and Dan Korman for helpful discussion on this point. ⮭
- I defend a similar argument in Barker (2021: §3). However, that argument differs from this one in a couple of important ways. First, that argument is one step in a larger argument against an entirely different thesis, the thesis that grounded entities are “ontologically innocent,” which is not the main target of this paper. Second, the argument of Barker (2021: §3) draws on a supervenience principle I call the Property Fixing Thesis (PFT), according to which the existence and properties of grounded entities generally supervene with metaphysical necessity upon the existence and properties of their full grounds. However, thanks to helpful feedback from referees at Ergo, the argument in Section 3 of this paper bypasses the supervenience step and argues directly from groundmates to the falsity of Purity. ⮭
- Note that this inference does not rely on Leibniz’s Law, according to which numerical distinctness suffices for qualitative difference. Rather, I am relying on an even less controversial assumption, namely, that numerical distinctness suffices for difference in either qualitative properties or difference in non-qualitative properties. For example, perhaps the only difference between grounded entity a and its groundmate, grounded entity b, is a haeccaetisic difference—ex. that a has the property being identical with a, but b lacks that property. Thanks to Ross Cameron for helpful discussion on this point. ⮭
- Indeed, since grounded entities a and b were selected arbitrarily, the argument of this paragraph shows that there is a GMD fact about every grounded entity with a groundmate. ⮭
- Given the standard assumption that grounding is asymmetric, [a is F] cannot serve as the GMD fact that helps ground [a is G] since [a is G] helps ground [a is F]. ⮭
- As Scott Dixon (2016: 466) shows, WF does not entail that full grounding is well-founded in the sense that every chain of full grounding eventually terminates in something(s) fundamental. WF is consistent with an infinitely descending chain of derivative or grounded entities such that each entity in the chain is both fully grounded in the subsequent grounded entity in the chain and is also fully grounded in at least one fundamental entity “outside” the chain. See Dixon’s (2016: §6) discussion of “fully pedestaled” chains of full grounding. Also see Rabin and Rabern (2016). ⮭
- Consider the following modal recombination principle:
Karen Bennett has argued that MR implies GGT (Bennett 2011a; 2017: 190–91). Nevertheless, MR provides no independent motivation for GGT, separate and apart from Purity. For if Purity is false, then MR is false as well. Suppose there is some contingent fact that violates Purity. For example, suppose that grounded entity x is F, and yet [x is F] is a fundamental fact. Weak Foundationalism demands that there be some fundamental entity that serves as the ultimate grounds for every grounded entity (§2). The fundamental fact [x is F] cannot be grounded entity x’s ultimate fundamental grounds. For entity x is a constituent of the fact [x is F]. So there must be some distinct entity, entity y, that serves as the ultimate fundamental grounds of entity x. Moreover, entity y must be contingent rather than necessary. If entity y were necessary, then whatever it fully grounded would also exist necessarily. Yet grounded entity x, which entity y fully grounds, is contingent. So entity y is also contingent. Finally, note that full grounding is necessitating—if a fully grounds b then, necessarily, if a exists then b exists. It follows that, necessarily, if entity y exists then entity x exists as well. Therefore, there are two contingent fundamental entities, entity x and entity y, which are not modally recombinable in the way that MR demands. I conclude that if Purity is false, then so is MR. Thanks to an anonymous referee at Ergo for encouraging me to address MR’s role in motivating Purity. ⮭Modal Recombination (MR): if entity x is a contingent and fundamental entity then, for any distinct contingent and fundamental entity y, it is possible for x to exist without y.
- Principle is similar to Daniel Nolan’s (2001) account of the difference between vicious and benign infinite regresses. Commitment to any infinite regress, Nolan argues, entails infinitely many new quantitative ontological commitments. Thus every infinite regress is theoretically costly. A regress is vicious, he argues, when this cost is not worth paying. Likewise, Principle instructs us only to reject those unmotivated theses that lead to an infinite regress of fundamental facts. Principle does not require us to reject a well-motivated thesis whose truth implies such a regress of fundamental facts. ⮭
- And see Bennett (2017: 196–98) for an updated discussion of her position. ⮭
- Thanks to Jim Darcy for helpful discussion of the material in this section. ⮭
- Daniel Z. Korman is perhaps conservatism’s most prominent defender. See especially Korman (2015). Also see Markosian (1998) for a view that is consistent with conservatism but does not entail it. For critical discussion of conservatism, see Fairchild and Hawthorne (2018). ⮭
- Defenders of unrestricted composition include Lewis (1986), Rea (1998), and Sider (2001). See van Inwagen (1990: 72–80) for discussion of SCQ and unrestricted composition. ⮭
- Most—though not all—defenders of restricted composition are anti-criterialists. Cf. Sanford (1993), Markosian (1998), Merricks (2001; 2005), Markosian (2008), Silva (2013), and Korman (2015). The most notable exception is Peter van Inwagen’s view, according to which some xs compose a y iff their activities jointly constitute a biological life. ⮭
- Van Inwagen’s neglected General Composition Question (GCQ) asks: “What is composition?” If specifying what it is to be F is just a matter of specifying F’s full grounds, then perhaps GCQ and FCQ are variants of the same question. On the other hand, if F’s full grounds need not reveal what it is to be F—if, say, the grounded need not be analyzed as or reducible to its full grounds—then GCQ and FCQ are different questions. See van Inwagen (1990: 39). ⮭
- Ned Markosian is brutal composition’s most prominent defender. See Markosian (1998) and (2008). ⮭
- Markosian discusses a view like this one, the “Multi-Factor Approach” (2008: §10). ⮭
- Although see Markosian (1998: §5) for a rejoinder to the counterintuitiveness objection to brutal composition. ⮭
References
4 Barker, Jonathan (2020). Debunking Arguments and Metaphysical Laws. Philosophical Studies, 177(7), 1829–55.
5 Barker, Jonathan (2021). Grounding and the Myth of Ontological Innocence. Australasian Journal of Philosophy, 99(2), 303–18.
6 Bennett, Karen (2011a). By Our Bootstraps. Philosophical Perspectives, 25(1), 27–41.
7 Bennett, Karen (2011b). Construction Area (No Hard Hat Required). Philosophical Studies, 154(1), 79–104.
8 Bennett, Karen (2017). Making Things Up. Oxford University Press.
10 Carnino, Pablo (2016). Grounding is Not Superinternal. Thought: A Journal of Philosophy, 5(4), 24–32.
11 Correia, Fabrice and Benjamin Schnieder (2012). Grounding: An Opinionated Introduction. In Fabrice Correia and Benjamin Schnieder (Eds.), Metaphysical Grounding: Understanding the Structure of Reality (1–36). Cambridge University Press.
12 Dasgupta, Shamik (2014). The Possibility of Physicalism. Journal of Philosophy, 111(10), 557–92.
13 Dasgupta, Shamik (2016). Metaphysical Rationalism. Noûs, 50(2), 379–418.
15 deRosset, Louis (2013). Grounding Explanations. Philosophers’ Imprint, 13(7), 1–26.
16 Dixon, T. Scott (2016). What Is the Well-Foundedness of Grounding? Mind, 125(498), 439–68.
17 Fairchild, Maegan and John Hawthorne (2018). Against Conservatism in Metaphysics. Royal Institute of Philosophy Supplement, 82, 45–75.
21 Fine, Kit (2010). Some Puzzles of Ground. Notre Dame Journal of Formal Logic, 51(1), 97–118.
22 Fine, Kit (2012). Guide to Ground. In Fabrice Correia and Benjamin Schnieder (Eds.), Metaphysical Grounding: Understanding the Structure of Reality (37–80). Cambridge University Press.
23 Glazier, Martin (2016). Laws and the Completeness of the Fundamental. In Mark Jago (Ed.), Reality Making (11–37). Oxford University Press.
25 Korman, Daniel Z. (2015). Objects: Nothing Out of the Ordinary. Oxford University Press.
27 Lewis, David (1986). On the Plurality of Worlds. Blackwell.
29 Litland, Jon Erling (2017). Grounding Ground. In Karen Bennett and Dean Zimmerman (Eds.), Oxford Studies in Metaphysics (Vol. 10, 259–316). Oxford University Press.
30 Markosian, Ned (1998). Brutal Composition. Philosophical Studies, 92(3), 211–49.
31 Markosian, Ned (2008). Restricted Composition. In Theodore Sider, John Hawthorne, and Dean W. Zimmerman (Eds.), Contemporary Debates in Metaphysics (341–63). Blackwell.
32 Merricks, Trenton (2001). Objects and Persons. Oxford University Press.
33 Merricks, Trenton (2005). Composition and Vagueness. Mind, 114(455), 615–37.
34 Merricks, Trenton (2013). Three Comments on Theodore Sider’s Writing the Book of the World. Analysis, 73(4), 722–36.
36 Nolan, Daniel (2001). What’s Wrong with Infinite Regresses? Metaphilosophy, 32(5), 523–38.
37 Rabin, Gabriel Oak and Brian Rabern (2016). Well Founding Grounding Grounding. Journal of Philosophical Logic, 45(4), 349–79.
38 Raven, Michael J. (2015). Ground. Philosophy Compass, 10(5), 322–33.
39 Raven, Michael J. (2016). Fundamentality without Foundations. Philosophy and Phenomenological Research, 93(3), 607–26.
40 Rea, Michael C. (1998). In Defense of Mereological Universalism. Philosophy and Phenomenological Research, 58(2), 347–60.
41 Rosen, Gideon (2010). Metaphysical Dependence: Grounding and Reduction. In B. Hale and A. Hoffmann (Eds.), Modality: Metaphysics, Logic, and Epistemology (109–36). Oxford University Press.
43 Saenz, Noël B. (2017). The Disciplining of Grounding. Unpublished manuscript.
44 Sanford, David H. (1993). The Problem of the Many, Many Composition Questions, and Naive Mereology. Noûs, 27(2), 219–28.
49 Schaffer, Jonathan (2017a). The Ground Between the Gaps. Philosophers’ Imprint, 17(11), 1–26.
50 Schaffer, Jonathan (2017b). Laws for Metaphysical Explanation. Philosophical Issues, 27(1), 302–21.
51 Sider, Theodore (2001). Four-Dimensionalism. Oxford University Press.
52 Sider, Theodore (2011). Writing the Book of the World. Oxford University Press.
54 Silva, Paul (2013). Ordinary Objects and Series-Style Answers to the Special Composition Question. Pacific Philosophical Quarterly, 94(1), 69–88.
58 van Inwagen, Peter (1990). Material Beings. Cornell University Press.
59 Wasserman, Ryan (2017). Vagueness and the Laws of Metaphysics. Philosophy and Phenomenological Research, 95(1), 66–89.
60 Wilsch, Tobias (2015). The Nomological Account of Ground. Philosophical Studies, 172(12), 3293–12.
61 Wilsch, Tobias (2016). The Deductive-Nomological Account of Metaphysical Explanation. Australasian Journal of Philosophy, 94(1), 1–23