Prefaces, Knowledge, and Questions

Frank Hong; Frank Hong

doi:10.3998/ergo.4631

1. Introduction

“We know a lot”.¹ At least, that’s what one might think. But as has been noted by Hawthorne (2003), Benton (2017), and Hawthorne (2002), a preface paradox for knowledge may bring that assumption into question. Here is a variant of such a paradox. Consider Xin, a person who purportedly knows a lot, and at time $t 0$ she writes a lot of things she thinks she knows. They range from things she has come to believe on the basis of perception (e.g., that there is a dog in her backyard) to things she has come to believe on the basis of testimony (e.g., that the Battle of Hastings took place in the year 1066) to things she has come to believe on the basis of a priori deduction (e.g., that the square root of $2$ is irrational). After producing her impressive book of purported knowledge, she suspects that there must be at least one error in there, and most likely more than one error. After all, hardly anyone has only true beliefs. Much to her surprise, at time $t 1$ God appears and tells her, “Impressive! Every proposition in this book is true, save one!”. In fact, of the $n + 1$ propositions in the book, propositions $p 1$ through $p n$ are all true, while $p n + 1$ is false. Delighted, Xin goes away thinking that she knew more than she originally thought—after all, Xin has now come to learn that she knows every proposition in that book save for one. Or does she? Given Closure, there may be good reasons to suspect that Xin does not know as much as she thinks she knows.

Closure: Necessarily, for any set of propositions $A$ , if for any proposition $p ∈ A$ , one knows $p$ , then one is in a position to know by deduction whatever is entailed by $A$ .

Consider the following argument. Suppose for reductio that Xin really does know all the true propositions in the book (i.e., $p 1$ through $p n$ ) at $t 1$ . Xin also knows at $t 1$ (from God’s testimony) that there is exactly one false proposition among $p 1$ through $p n + 1$ . Thus, if Xin knows all of $p 1$ through $p n$ , and Xin knows that there is exactly one false proposition among $p 1$ through $p n + 1$ , it follows from Closure that she is in a position to know that $p n + 1$ is false. But this is absurd. Even if Xin knows that there is exactly one false proposition in the book, it is prima facie implausible that she can be in a position to simply deduce which proposition is false. Thus, if Xin is not in a position to know which proposition is false at $t 1$ when she learns that there is exactly one false proposition in the book, then it follows from Closure that she is not in a position to know all of the true propositions $p 1$ through $p n$ at $t 1$ .

What is striking about this result is that very little is assumed about how Xin came to believe the things she has come to believe. Pick your favourite source of knowledge (e.g., perception, a priori deduction, testimony, etc.), and we can stipulate that each of the true individual beliefs that were produced by these sources of knowledge are safe and are without any defeaters (e.g., no fake barns, stopped clocks, or inferences from false premises). No matter how safe each of her individual beliefs are, no matter how competently she has formed them, the moment she learns that she has exactly one false belief, it follows that she also fails to know something else that is true.

So much for what Xin knows at $t 1$ . But what about $t 0$ ? Perhaps Xin knew all of $p 1$ through $p n$ and somehow her knowledge was lost when she heard from God. In Section 3.1, we will discuss this possibility that one’s knowledge is defeated when one learns that one has a single false belief. For now, it suffices to say that, for a set of beliefs like Xin’s, this possibility conflicts with a plausible principle connecting probability and defeat:

Defeating Evidence Is Not Confirming Evidence: If one knows $p$ , then evidence $E$ does not defeat one’s knowledge of $p$ if $P r (p | E) > P r (p)$ .

Now, what do I mean by a “set of beliefs like Xin’s”? For us, the important thing about Xin’s set of beliefs that gives rise to this puzzle is the fact that (1) Xin is very confident that there is at least one false belief in the set (recall how Xin was actually surprised that there was only one error among the set!), and (2) Xin has no special reason to think that any particular belief is false when she learns that she had exactly one false belief. I show in Section 3.1 that, since Xin’s sets of beliefs satisfy (1) and (2), Defeating Evidence Is Not Confirming Evidence implies that Xin cannot have lost any knowledge after learning that one of $p 1$ through $p n + 1$ is false.

Now, if none of Xin’s knowledge gets defeated when she learns that there is a single false proposition in the book, then this suggests that whichever of $p 1$ through $p n$ that Xin doesn’t know at $t 1$ , she never knew at $t 0$ either.

This suggests that at $t 0$ , the following is true of her epistemic state:

No Loss, No Gain: It is possible for Xin to learn that there is exactly one false claim in her book without:

(a): losing knowledge of any of $p 1$ through $p n$ . [No Loss]

(b): being in a position to know $¬ p n + 1$ . [No Gain]

However, No Loss, No Gain is jointly inconsistent with the following three assumptions:

Closure: Necessarily, for any set of propositions $A$ , if for any proposition $p ∈ A$ , one knows $p$ , then one is in a position to know by deduction whatever is entailed by $A$ .

Xin is Fallible: Xin does not know $¬ p n + 1$ .

Xin Knows A Lot: Xin knows all of $p 1$ through $p n$ .

To see how No Loss, No Gain, Closure, Xin is Fallible and Xin Knows A Lot are jointly inconsistent, first suppose Xin Knows A Lot. Since Xin Knows A Lot, it follows by Closure that Xin is in a position to know $p 1 ∧ … ∧ p n$ . If Xin learns that there is exactly one false claim in $A$ , then either Xin can come to know $¬ p n + 1$ by Closure, OR, Xin can’t come to know $¬ p n + 1$ by Closure. If Xin can come to know $¬ p n + 1$ by Closure, then No Gain is false. If Xin cannot come to know $¬ p n + 1$ by Closure, then that can only be because she has somehow lost her knowledge of one of $p 1$ through $p n$ , and so No Loss is false. Either way, both cases contradict No Loss, No Gain, and so the four assumptions are jointly inconsistent.

It is worth noting that this puzzle is related, but importantly different, from standard presentations of the Lottery and the original Preface Paradox. Like the lottery, we have a case where there are a great number of propositions, each of which is likely to be true, one of which is false, and where we do not know which one is false. In the case of the lottery, the propositions are all of the form ticket $i$ is going to lose. However, in standard presentations of the Lottery Paradox, one is supposed to have the intuition that one doesn’t know whether any of those propositions are true. I hope that in Xin’s case, however, you have the exact opposite intuition from the lottery case—that is, that for at least some of Xin’s beliefs, she knows whether they are true.²

Secondly, this case is similar to, but importantly different from, the original Preface Paradox as presented by Makinson (1965). That paradox is about rational belief. In Makinson’s setup, the author is rational in believing claims $p 1$ through $p n$ , but is also rational in believing $¬ (p 1 ∧ … ∧ p n)$ . The puzzle is that these beliefs are clearly inconsistent, but the author seems to be eminently rational in having each of these beliefs. Similarly, in Xin’s case, it may seem eminently rational for Xin to believe each of $p 1$ through $p n + 1$ but also believe (indeed, $know$ ) $¬ (p 1 ∧ … ∧ p n + 1)$ .

However, whereas the original paradox is about rational belief, the puzzle we have here is about knowledge. Indeed, what makes the Preface Paradox so puzzling for belief is that one can say in a preface, “I believe each claim in this book; otherwise, I wouldn’t have written these claims down! However, I am not so arrogant as to say that I believe that there are no errors in the book”. However, to produce our paradox for knowledge, it is not so simple a matter as to replace each occurrence of “believe” in the preface for the word “knows”. For one would not write in a preface: “I $know$ each claim in this book; otherwise, I wouldn’t have written these claims down! However, I am not so arrogant as to say that I $know$ that there are no errors in the book”. Whereas the former statement is a beautiful display of one’s humility, the latter claim sounds downright bizarre.

So what we have here is a Preface Paradox for Knowledge. What shall we say about it? Which assumption should be denied?

In this paper, I will argue that Xin Knows A Lot is false. Indeed, I argue Xin Doesn’t Know a Lot—that there is some true proposition in the book that Xin simply does not know.

However, as I argue for Xin Doesn’t Know A Lot, I want to distinguish my approach from two other possible approaches that make that claim trivially true. Those two approaches are both Infallibilist in nature: they both claim that knowledge requires certainty.

On the first Infallibilist approach, we say that Xin hardly knows anything at all since she is not certain in any of her beliefs. Moreover, since Xin is as good of an epistemic agent as they come, it follows that we too hardly know anything at all. Let us call this view a “Pessimistic Infallibilism” since infallibilists of this sort tend to be skeptics (see Unger 1971 as an example).

On the second Infallibilist approach, we say that knowledge requires certainty because our body of evidence E just is our body of knowledge K and a rational agent’s credences matches their prior probabilities conditional on all their evidence (see Williamson 2000). So for example, for any proposition $p$ that one knows, $P r (p | E) = 1$ , and so one should be certain in $p$ . Like the “Pessimistic Infallibilist” approach, this second kind of approach continues to say that Xin doesn’t know a lot since Xin is not certain in any of her beliefs.³ However, unlike Pessimistic Infallibilism, this kind of Infallibilism does not necessarily say that Xin is as good of an epistemic agent as they come. Indeed, proponents of the E = K thesis would often say that, if we were rational, we should be certain in many propositions. Thus, though the E = K theorist might say that Xin (at least in how I described her in not being rationally certain in any of her beliefs) hardly knows anything, the E = K theorist may still say that we can still know many things. Let us call this kind of Infallibilist an “Optimistic Infallibilist”.

As I argue against Xin Knows A Lot, I eschew both these approaches. I am a die-hard Fallibilist. I believe that knowledge does not require certainty. And unlike the Pessimistic Infallibilist, I am not a skeptic. And unlike the Optimistic Infallibilist, I do not regard us as any better than Xin. If not even Xin can know a lot, then neither can we.

Indeed, I argue that we do not know a lot because we are similar to Xin at $t 0$ . For just as (1) Xin is confident that there is at least one error among her beliefs, so am I that I have at least one error among my beliefs. And just as (2) Xin has no special reason to think that any particular belief of hers is false if exactly one of her beliefs is false, so too I have no special reason to think that any particular belief of mine is false if exactly one of my beliefs is false. In fact, this is true of me for even just a fraction of the beliefs I have gained in my lifetime. For example, after talking to some friends, reading bits of news, and a few chapters of a book in the last week, I have come to acquire many beliefs, and I am quite confident that I have acquired at least one false belief. Furthermore, I have no special reason to think that any particular belief is more likely to be false if only one of my beliefs is false.

And so, since the set of beliefs I have gained this past week is relevantly similar to the set of beliefs Xin has written down in her book, if Xin could not know all the true propositions she believes at $t 0$ , then so too am I unable to know all the true propositions I have come to believe in the past week. And compared to all the beliefs I have gained in my lifetime, if I cannot even come to know all the true propositions I have come to believe in the past week, then I don’t know very much at all. Thus, since Xin doesn’t know a lot, I argue for:

Socraticism: We do not know a lot.

Socraticism is so called because, if true, it would mean that Socrates was right all along to be suspicious of those who claim to know much when in fact they know very little. Indeed, if Socraticism is true, it would mean that we all don’t know as much as we ordinarily think we do, and not just Socrates’s overconfident interlocutors.

I should also note that the claim that we do not know “a lot” is distinct, but related, from the claim that we do not know a “large number of propositions”. Clearly, if one knows a lot of things, then one would also know a large number of propositions, but not vice-versa. One can know some proposition $p$ , and also be in a position to know $p ∨ q$ , and $p ∨ q ∨ r$ , and so on. If someone only knew $p$ and all its logical consequences, such a person would know a large number of propositions, but such a person would hardly count as someone who “knows a lot”. At the very least, someone who “knows a lot” would be someone who knows a large number of propositions that are not too dependent on each other.⁴

As surprising as this claim is, I will be defending Socraticism. Both I and the Skeptic (who argues that we don’t know anything at all except some a priori truths and perhaps some other truths of which we are certain) can agree on Socraticism. However, I depart from the Skeptic on two accounts. Firstly, I depart from the Skeptic in that I still think that we know some a posteriori things of which we aren’t certain. I just think that we do not know nearly as much as we think we know.

Secondly, I depart from the Skeptic in that I think that many of our knowledge ascriptions such as “A knows that p” are true. This is because I will be giving a contextualist model where “knows” expresses different relations in different contexts. So, whereas many of our knowledge ascriptions may not be true in a single context, many of our knowledge ascriptions are still true in some contexts.

In Section 2, I give my own model that is consistent with No Loss, No Gain and Closure, while still vindicating the idea that many of our knowledge ascriptions are true. I discuss some advantages of my model, including the fact that it can reconcile Closure with another plausible principle: Modesty. Modesty is the principle that one is justified in believing that not all of one’s beliefs are true. In Section 3, I explore the consequences of denying No Loss, No Gain.

In the following, I will take Closure for granted. Indeed, the costs for denying Closure are quite high. Stephen Yablo recalls that Kripke used to make vivid the implausibility of denying Closure by exclaiming, when giving a deductive argument with irreproachable reasoning, “Oh no, I’ve just committed the fallacy of logical deduction!” (Yablo 2014: 116). Still, perhaps the conclusion Socraticism is reason to place Closure under suspicion. I hope, however, that the contextualist model about to be presented will be able to take the sting away from Socraticism, vindicate most of our knowledge ascriptions, and make some headway into resolving the the original Preface Paradox, all without giving up Closure.⁵

2. A Contextualist Solution

Contextualism is a view about how the word “knows” can vary in its semantic value depending on speaker context. Thus, there is no single relation, $knows$ , that is expressed by “knows” in every context. Instead, we have a plethora of knowledge relations—we have the relation $know s 1$ , $know s 2$ , … etc., and any of these relations can be expressed by the word “knows” in some context.

Contextualism is particularly well-suited for defending Closure⁶ from counter-examples. For example, it is intuitive to think that one can easily know whether one’s car is in the parking lot, but also intuitive to think that one does not know whether one’s car has in fact been stolen in the last hour. However, one also knows that if one’s car is in the parking lot, then the car has not in fact been stolen in the last hour. Closure would then seem to imply that one both knows, and doesn’t know, that one’s car is still in the parking lot. Fortunately, contextualists have a ready solution. One $know s 1$ that the car is still in the parking lot, and thereby also $know s 1$ (by Closure) that no thief has stolen the car. However, in a different context where one is considering the possibility of a thief lurking in the neighborhood, or if the stakes of a stolen car are high, or (insert one’s preferred explanation for context shift here), “knows” might express the relation $know s 2$ , and one may fail to $kno w 2$ that a thief stole the car and thereby also fail to $kno w 2$ that one’s car is in the parking lot. So, contextualists can explain why, in some contexts, we are inclined to say that one “knows that the car is in the parking lot” while in other contexts refrain from saying that one “knows that a thief didn’t steal the car” without impugning Closure.

However, things are a little different with our puzzle. After God speaks, the contextualist must offer an explanation for why we are not reluctant to say “Xin knows $p i$ ” for any $i$ from $1$ to $n$ , but are somehow reluctant to also say “Xin is in a position to know $¬ p n + 1$ ”. For a contextualist solution to work, one cannot simply say that Xin $know s 1$ each of $p 1$ through $p n$ , but is not in a position to $kno w 2$ $¬ p n + 1$ . For if a contextualist says this, then one must admit that Xin is in a position to $kno w 1$ , by Closure, $¬ p n + 1$ . But unlike knowing whether a thief has stolen a car, it is implausible that “Xin is in a position to know $¬ p n + 1$ ” is true in any context.

Broadly speaking, in order for a contextualist solution to work, we need to have reason to believe that for each $p i$ from $p 1$ to $p n$ , there is some context $c i$ such that “Xin knows $p i$ ” is true relative to $c i$ , but that there is no single context $c a$ where all of those utterances are true. Thus, we need a picture that accepts the following combo:

Combo A

“Xin knows $p 1$ ” is true relative to context $c 1$

“Xin knows $p 2$ ” is true relative to context $c 2$

.

“Xin knows $p n$ ” is true relative to context $c n$

But we do not want a single context $c a$ such that:

Combo B

“Xin knows $p 1$ ” is true relative to context $c a$

“Xin knows $p 2$ ” is true relative to context $c a$

.

“Xin knows $p n$ ” is true relative to context $c a$

For if there were such a context, then Closure would imply that there is some relation $know s a$ such that Xin is in a position to $know s a$ $¬ p n + 1$ , and thus, “Xin is in a position to know $¬ p n + 1$ ” would be true in some context.

So, can a contextualist accept Combo A, but reject Combo B? On the two most common kinds of contextualism (“Standard-Shifting” Contextualism and Lewisian Contextualism), the answer is “no”. Let us see why for each in turn.⁷

2.1. “Standard-Shifting” Contextualism

On a “Standard-Shifting” contextualism, the contextually salient parameter that shifts from context to context is one’s “epistemic standard”. One example of this kind of contextualism is DeRose’s contextualism, where the meaning of “S knows that $p$ ” is something like, “S has a true belief that $p$ , and is in a good enough epistemic position with respect to $p$ ” (DeRose 2009: 3), where “good enough epistemic position” varies with the context. How “good” one’s epistemic position is is determined by the epistemic standards of the context. When the standards are high, “knows” expresses $know s high$ , and it is very difficult to $kno w high$ many things. On the other hand, when the standards are low, “knows” expresses $know s low$ , and one presumably can $kno w low$ many things.

But this view would not help with our puzzle at hand. For presumably, Xin has evidence par excellence for believing each of $p 1$ through $p n$ . Thus, she should $kno w low$ each of $p 1$ through $p n$ . But if that is the case, then we have a knowledge relation that satisfies Combo B, and Closure would then imply that Xin is in a position to $kno w low$ $¬ p n + 1$ .

Furthermore, it is no help to consider contexts in which the standards are higher either. For no matter what the standards are, Xin’s true beliefs either all meet the standard (and so they all count as knowledge), or they all fail the standard (and so none count as knowledge). Thus, no matter the standards, either we get Combo A and Combo B together, or we get neither. What we want, however, is a contextualist model that offers Combo A without Combo B.

In general, any kind of contextualism that works by shifting “standards” from context to context will be unable to solve our puzzle. For example, consider a kind of contextualism where one can only know a proposition if one’s credence in that proposition conditional on one’s evidence is “sufficiently high”, where “sufficiently high” is context sensitive. For example, a sentence like “Xin knows that $p i$ ” might be true in a low standards context where Xin only needs to be about $0.9$ certain in $p i$ , but “Xin knows that $p i$ ” might be false in a high standards context where Xin needs to be at least $0.9999$ certain in $p i$ . But this solution won’t work because, on this view, Xin can still $kno w low$ $p i$ for any $i$ . Thus, Closure will imply that Xin is in a position to $kno w low$ $¬ p n + 1$ .⁸

The problem with contextualist views where the shifting contextually salient parameter is some “epistemic standard” is that one can always stipulate a case where, for many propositions, one meets that standard for each of those propositions. Thus, no matter what the standards are, or how they shift, we can just stipulate that Xin meets some standard for $n$ true propositions. But once we have such a case, we have Combo B, and Closure would then imply that “Xin is in a position to know $¬ p n + 1$ ” is true in that context where that epistemic standard is at play.

Now, defenders of the “shifting-standards” approach may say that whenever we utter, “Xin is not in a position to know $¬ p n + 1$ ”, any epistemic standard under which we would know $p 1$ through $p n$ are never at play, and so these are contexts in which we should be able to say of any $p i$ that Xin is not in a position to know $p i$ . But this is a bit odd. When we say, “Xin is not in a position to know $¬ p n + 1$ ”, we should be able to say so without kicking the epistemic standards into ultra high-gear. It is not as if, when we deny Xin’s knowledge of $¬ p n + 1$ , we are suddenly Cartesian infallibilists who are prepared to also deny that Xin knows her own name. We simply deny that Xin is in a position to know $¬ p n + 1$ because she falsely believes in its negation, and so we should be able to deny that she is in a position to know $¬ p n + 1$ even when the standards of knowledge are very low.⁹ What we would like to be able to do is to deny, in one context, that Xin is in a position to know $p n + 1$ $without$ having to deny Xin’s knowledge of all of $p 1$ through $p n$ ; and we would like to be able to be able to affirm, in one context, that Xin is in a position to know one of $p 1$ through $p n$ without consequently having to affirm that she knows all of $p 1$ through $p n$ and thereby be in a position to know $¬ p n + 1$ by Closure.

What we need, then, is a contextualist view where one can only know relatively few propositions in each context. The problem with “standard-shifting” contextualist views is that, once we have a contextually salient standard, there is no limit to how many propositions meet that standard. But once we have that kind of contextualist feature, we will have a difficult time accepting Combo A while rejecting Combo B. Let’s see if Lewisian contextualism fares any better.

2.2. Lewisian Contextualism

We have seen how “standard- shifting” contextualist views are inadequate for solving our puzzle at hand. Lewis, for different reasons, also rejected the “standard-shifting” contextualist view:

If you start from the ancient idea that justification is the mark that distinguishes knowledge from mere opinion (even true opinion), then you well might conclude that ascriptions of knowledge are context-dependent because standards for adequate justification are context-dependent…But I myself cannot subscribe to this account of the context-dependence of knowledge, because I question its starting point. I don’t agree that the mark of knowledge is justification. (1996: 550–51)

On Lewis’s view, as expounded in “Elusive Knowledge”, S knows proposition P iff:

P holds in every possibility left uneliminated by P’s evidence; equivalently, iff S’s evidence eliminates every possibility in which not-P. (1996: 551)

Here, the word “every” is context sensitive. In some contexts, “every” quantifies over possibilities where S is a handless Brain-In-A-Vat (BIV), and sometimes not. In the context where “every” quantifies over possibilities where S is a BIV, S’s evidence needs to rule that possibility out if “S knows that S has hands” is to be true in that context.¹⁰ In a context where “every” does not quantify over such a possibility, S’s evidence need not rule out that possibility in order for “S knows that S has hands” to be true in that context.

So what matters for Lewis is not that our epistemic standards shift from context to context; rather, his contextualism for knowledge reduces to a familiar kind of contextualism about the domain of quantification. In explaining how the extension of “knows” shifts from context to context, then, Lewis only needs to explain how the domain of quantification over possibilities shifts from context to context.

For Lewis, what determines which possibilities are quantified over depends on which possibilities are not being “properly ignored”. Lewis then proceeds to give seven rules that determine which possibilities are not properly ignored. I will only highlight four of the rules: (1) The Rule of Actuality—the possibility that actually obtains is not properly ignored; (2) The Rule of Belief—any possibility which S believes to obtain is not properly ignored, (3) The Rule of Resemblance—if two possibilities saliently resemble each other (where what counts as “salient” is also determined by context), then either both possibilities are properly ignored, or neither are properly ignored, and (4) The Rule of Attention—any possibility that is not being ignored is not being properly ignored.

Lewis himself used the Rule of Actuality and the Rule of Resemblance to attempt to explain why one does not know that one would lose the lottery. Since the possibility where your ticket wins saliently resembles any other ticket winning, one can only properly ignore the possibility where your ticket wins if one can ignore the possibility of any ticket winning. But, by the Rule of Actuality, one cannot properly ignore the possibility where the actual winning ticket wins, and so one cannot, by the Rule of Resemblance, properly ignore the possibility where one’s own ticket wins.

At first blush, Lewis’s contextualism may be just what we need for our own contextualist solution. After all, in some context, the actual possibility where $p n + 1$ is false does saliently resemble the possibility that any of the other $n$ propositions are false. The possibility that any of the $n$ propositions are false saliently resembles the possibility where $p n + 1$ is false because these are all worlds where Xin has written down exactly one false proposition. Thus, there is some context where Xin does not know any of $p 1$ through $p n$ , and so there is a context in which Xin is not in a position to know $¬ p n + 1$ by Closure. Nonetheless, this does not preclude the possibility of Xin knowing the other $n$ propositions in some other context. Thus, although there is a context in which Xin is not in a position to know $¬ p n + 1$ , this fact does not preclude the existence of a context where Xin does know $¬ p n + 1$ .¹¹

So Lewis’s contextualism does not go far enough. We need a contextualist solution that not only prevents “Xin is in a position to know $¬ p n + 1$ ” from being true in some context, we need a contextualist solution that prevents that sentence from being true in all contexts. And on Lewis’s, view, the rules at hand do not prevent “Xin knows $p i$ ” for all $i ≤ n$ from being true in a single context. Even if the actual world is one where $p n + 1$ is false, there is no reason to think that this possibility always saliently resembles possibilities where one of the other $n$ propositions are false. For example, $p n + 1$ may be a proposition about the weather, and every other proposition may be about some major historical event, and so there could be a context where a possibility in which the weather proposition is false does not saliently resemble at all the possibilities where one of the historically important propositions are false.

To resolve this issue, Hawthorne (2003) proposes an extra rule: the New Rule of Belief:

New Rule of Belief: If the proposition that P is given sufficiently high credence—or ought to be—by the subject, then one cannot properly ignore all of the possibilities that constitute subcases of P.

In our case, proposition P would be the proposition that one of $p 1$ through $p n$ is false. Assuming that there are $1000$ propositions, and that Xin becomes $0.999$ confident in each proposition when she learns she wrote down only one false proposition, she should be $0.999$ confident that $p n + 1$ is true, and so she should be $0.999$ confident that the false proposition is one of $p 1$ through $p n$ . Assuming, as is plausible, that $0.999$ is a sufficiently high credence, the New Rule of Belief implies that Xin cannot properly ignore all of the possibilities that constitute subcases of P. In other words, Xin cannot ignore the possibility that $p 1$ is false and the possibility that $p 2$ is false and… and the possibility that $p n$ is false. The New Rule of Belief essentially puts an upper limit to how many possibilities Xin can properly ignore. So, no matter the context, Xin can only properly ignore relatively few possibilities, and she cannot properly ignore the rest. For example, if the threshold for “sufficiently high” for P is $0.9$ , then of the $n$ propositions, Xin can only properly ignore all the possibilities that together are given only $0.1$ credence. In Xin’s case, that means she can only properly ignore up to $100$ possibilities where one of $p 1$ through $p n$ are false.

This solution brings us tantalizingly close to a solution. It would seem that with the New Rule of Belief, we can make sense of the fact that Xin can only know relatively few propositions per context, and that for every proposition from $p 1$ to $p n$ , there is in principle a different context where Xin can know each of them. Thus, we seem to be able to both accept Combo A and deny Combo B.

However, the New Rule of Belief doesn’t quite bring us this far. It only implies that Xin can only properly ignore relatively few possibilities per context. This does not yet mean that Xin can only $know$ relatively few propositions per context, since those possibilities that remain unignored may still be ruled out by Xin’s evidence. For example, the New Rule Belief may imply that if Xin is properly ignoring all the possibilities where $p 1$ through $p 100$ are false, then she cannot be properly ignoring the possibilities where one of $p 101$ through $p 1000$ are false. But nothing precludes us from saying that Xin’s evidence rules out those possibilities which she is not properly ignoring.

To make it concrete, suppose that Xin is simply attending to a possibility where $p 101$ is false. By the Rule of Attention, she is not properly ignoring that possibility. Let’s say $p 101$ is the proposition that Xin’s friend emailed her a computer program that, once executed, produces the text of all of Hamlet. Suppose Xin is attending to the possibility that her friend did not actually email her such a program, but had instead emailed her a random text generator. Indeed, we could even imagine the scenario as if Xin’s friend emails the program, but later asks Xin whether she mistakenly emailed the random text generator program she was working on. Once Xin’s friend asks this question, the possibility of her sending a random text generator is no longer properly ignored. Nonetheless, Xin could easily rule out that possibility upon executing the program several times and observing that it produces all of Hamlet each time. In fact, such a procedure would be a perfectly good example of how Xin could come to learn which program her friend actually sent her (after all, most of us can come to know what a program does when we run the program). So if her evidence is good enough to rule out the possibility that her friend sent a random word generator when she raised the question, it is plausible that her evidence is still good enough to rule out that possibility even when she attends to it again later.

In this example, we don’t even need the New Rule of Belief to say that she cannot be properly ignoring a possibility where $p 101$ is false. Nonetheless, we can still say that Xin’s excellent evidence still rules out the possibility.¹²

Still, the New Rule of Belief gives us a hint of what we must do. What we need is not a picture where there is a limit to how many possibilities we can properly ignore per context; rather, we need a picture where there is a limit to how many possibilities we can rule out per context. My contextualism is just such a picture.

2.3. Question-Relative Contextualism

One simple way to impose a limit to how many possibilities one can rule out is to set a credence threshold to which propositions can even be believed. In the language of possible worlds, we can revise Hawthorne’s New Rule of Belief like so:

Brand New Rule of Belief If the proposition that $P$ is given sufficiently high credence—or ought to be—by the subject, then one cannot rule out all the possible worlds $w$ s.t. $w ∈ P$ (i.e., there must be some $w ∈ P$ which we cannot rule out).

This Brand New Rule of Belief is related to the Lockean Thesis for belief which states that belief is just confidence over a threshold. The motivation for the Brand New Rule of Belief is that one cannot come to know a proposition where one is not even confident enough to believe that proposition. However, one need not adopt the entirety of the Lockean Thesis to motivate the Brand New Rule of Belief. One need only to say that confidence over a threshold is a necessary condition for belief, and not necessarily a sufficient condition.

However, although the Lockean Thesis can motivate the Brand New Rule of Belief, the Lockean Thesis is one that is profoundly difficult to reconcile with any view of belief and knowledge that accept Closure. This is because, on the Lockean Thesis, Xin would count as believing (and possibly knowing) each of $p 1$ through $p n$ since Xin is sufficiently confident in each, but Xin could not even believe, let alone know, $p 1 ∧ … ∧ p n$ since Xin’s credence in that proposition is too low.

So, how can we square the Brand New Rule of Belief with Closure? A naive contextualism that makes “sufficiently confident” context sensitive will do no good here. For the only thresholds where $p 1$ through $p n$ and $p 1 ∧ … ∧ p n$ are all believed would be thresholds that are implausibly low (Xin would count as believing almost anything). And the only thresholds where none of $p 1$ through $p n$ and $p 1 ∧ … ∧ p n$ are believed will be implausibly high (Xin would count as believing almost nothing at all). In most contexts, then, Xin’s credence in each of $p 1$ through $p n$ would be over the threshold for belief, while her credence in $p 1 ∧ … ∧ p n$ would be under the threshold for belief. Thus, in most contexts, what she believes (and therefore, what she knows) would not be closed under deduction.

One way of squaring the Brand New Rule of Belief with Closure is to aim for a contextualist view where “worlds we cannot rule out” is context sensitive. In particular, “worlds we cannot rule out” will be sensitive to a specific question.

To do this, we will introduce a formal model and first define a doxastic accessibility relation $R B$ that encodes the Brand New Rule of Belief, and then define an epistemic accessibility relation $R K$ based on $R B$ . We then apply our model to the Preface Paradox for knowledge and then we will apply our model to the Preface Paradox for rational/justified belief.

2.3.1. Formal Model for Question-Relative Contextualism

Here enters my model. Our model is an ordered quadruple $< W, ℬ, P, P r >$ where $W$ is a set of possible worlds, $ℬ$ is a Boolean $Σ$ -Algebra over worlds,¹³ $P$ is a partition on those worlds, and Pr is a probability function defined over the elements of $ℬ$ . As usual, propositions are modeled as sets of worlds and, following Groenendijk and Stokhof (1984), a partition models a question. For example, the proposition that James is at the party is just the set containing all the worlds where James is at the party, and the question whether James is at the party is the partition {James is at the party; James is not at the party}.

Given this model, we can now define a plausibility relation among worlds, $> >$ (read as “way more plausible than”), like so:

Definition 1. $w > > w ′ iff P r (| w |) P r (| w ′ |) > t when P r (| w ′ |) ≠ 0$ ¹⁴

where | $w$ | denotes the proposition in the partition that $w$ is an element of, and $t$ is some threshold greater than 1 (let’s say 10).¹⁵ For an entirely different use of partitions in modelling beliefs, see Yalcin (2018).

The motivation for introducing this plausibility relation is the idea that there are certain propositions that we can simply rule out by default for being too implausible. For example, relative to the question {I am a brain in a vat; I am not a brain in a vat}, we can simply rule out the worlds where I am a brain in a vat so long as it is much less probable than the proposition that I am not a brain in a vat and it is false. In setting up things this way, we also do justice to the Fallibilist intuition that we can know things without being absolutely certain. For example, we do not need to be certain that we are not brains in a vat to know that we aren’t; the proposition simply needs to be way more implausible than it’s negation relative to the question “are we brains in a vat?”.

Given this plausibility relation, we can now define $R B$ , our function that takes possible worlds $w ∈ W$ to the strongest proposition one is justified in believing at that world. As a first pass, we can define $R B$ like so:

Definition 2. $R B (w) = {w ′ : ¬ ∃ w ″ (w ″ > > w ′)}$ ¹⁶

In other words, the set of worlds doxastically accessible to a world $w$ are the worlds such that there are no other worlds way more plausible than it. An important thing to note about $R B$ is that its value does not depend on which particular world it takes as its argument. $R B$ gives you the same proposition no matter what world you are in. In other words, what you are justified in believing does not depend on the actual state of the world, it only depends on our degrees of belief about the world and the question we are considering.

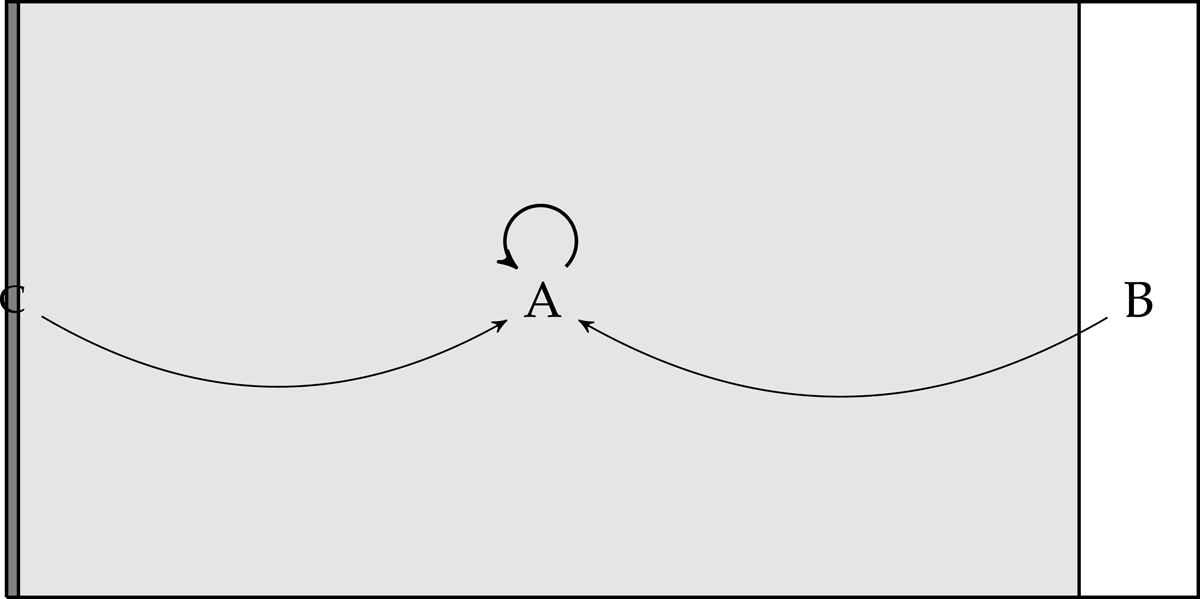
For a graphical illustration, suppose one is looking at a red wall and one is certain that one of the following things is true: (A) The wall is red, (B) The wall is white with trick lighting, (C) One is a BIV and there is no wall. Accordingly, $P r (A) = 0.99$ , $P r (B) = 0.01 − ϵ$ , and $P r (C) = ϵ$ .

In such a situation, what is one justified in believing? The answer is easy, one is justified in believing that the wall is red because the A-worlds are the most plausible worlds. Since $P r (A) P r (B) > 10 and P r (A) P r (C) > 10$ , one is by default justified in believing that one is neither in the B-worlds nor the C-worlds, and so one is justified in believing that we are in a A-world.

Figure 1

Red Wall, White Wall, or BIV? Justified Belief

Fig. 1 above is an illustration to make clear what one is justified in believing relative to the question ${A; B; C}$ . Fig. 1 represents how the probabilities are distributed over the set of worlds, where the size of the regions roughly represent the relative proportions of their probabilities, and the arrows show which worlds are doxastically accessible to which other worlds.

An easy, effective procedure to determine which worlds belong to $R B (w)$ is to follow the following steps:

Effective Procedure To Determine $R B (w)$

Find the biggest cell or cells (i.e., the most probable cell) in the partition, and add all the worlds in those cells to $R B (w)$ .
Next, find all the cells that are of similar size to the biggest cells (i.e., find the cells that are notover ten times smaller than the biggest cells), and add all the worlds in those cells to $R B (w)$ .
You are done!

The problem with this definition, however, is that it is consistent with one being justified in believing a very improbable proposition. For example, if we are playing a rigged lottery where we are certain that ticket 1 has a 1% chance of winning while tickets 2 through 1001 each have a $0.099 %$ chance of winning, then relative to the question “which ticket will win?” one would be justified in believing that ticket 1 will win simply because it is much more probable than all the alternatives.¹⁷

To avoid the result that there are some contexts where one is justified in believing in incredibly improbable propositions, we need to encode our Brand New Rule of Belief into our definition of $R B$ . Thus, the following will be our official definition:

Let us define our doxastic accessibility relation $R B$ like so:

Definition 3. $R B (w) = ∪ i R i B$ for $i < k$ the smallest k s.t. $P r (∪ i R i B) > t$ (where $0.5 < t < 1$ )¹⁸

We now define $R i B$ recursively as follows:

If $i = 0, R 0 B (w) = {w ′ : ¬ ∃ w ″ (w ″ > > w ′)}$
If $i = n + 1, R n + 1 B (w) = {w ′ ∈ {W − ∪ i = 0 n R i B | ¬ ∃ w ″ (w ″ > > w ′)}}$

Informally, $R B (w)$ is the strongest (not necessarily true) answer (or partial answer) to the question that is both probable and much more probable than any of its alternatives.¹⁹ And depending on the question, what the alternatives are can differ.

Our new definition of $R B$ encodes the spirit of the Brand New Rule of Belief because it prevents us from doxastically ruling out so many worlds such that the probability of one of those worlds obtaining exceeds some number $t$ which represents our threshold for belief. In other words, we cannot rule out so many answers to a question such that the only answer to the question we are left with is too improbable for us to even believe.

Again, we have an effective procedure to easily compute $R B (w)$ :

Effective Procedure To Determine $R B (w)$

Find the biggest cell (or cells) in the partition. Add all worlds in that cell (or cells) to $R B (w)$ .
Find all the cells that are of similar size to the biggest cell (i.e., cells that are not over ten times smaller than the biggest cell). Add all the worlds in those cells to $R B (w)$ if they are not already in.
While ( $Pr (R B (w)) < t$ , look at the group of cells that haven’t been added in yet, and then add the worlds in the much bigger cells (i.e., cells that are at least 10 times bigger than the other left over cells) into $R B (w)$ .
You are done!

When we apply this new definition to our rigged lottery case, we get the result that one is not justified in believing in anything (or one is justified in only believing tautologies) relative to the question “which lottery ticket will win?”. That is because, though the worlds where ticket 1 wins are the most plausible, they do not constitute a proposition with a probability over some threshold $t > 0.5$ . Thus, we need to add into $R B (w)$ our next batch of most plausible worlds. Since the next batch of worlds are all equiprobable, we add them all into $R B (w)$ . After we do that, we find that $P r (R B (w)) = 1$ (since we have now essentially added all the worlds in $W$ to $R B (w)$ ). Since $1 > t$ (let’s say $t = 0.91$ for concreteness), we stop adding any more worlds into $R B (w)$ , and now we see that $R B (w) = W$ . In other words, the only proposition one is justified in believing in the rigged lottery case is the tautology.

So much for justified belief. What about knowledge? Let $R K$ be our function that takes possible worlds $w ∈ W$ to the strongest proposition one knows at that world. Let us define $R K$ as follows:

Definition 4. $R K (w) = R B (w) ∪ {w ′ : ¬ (w > > w ′)}$ ²⁰

In other words, the strongest thing you know at a world $w$ is the proposition containing all the worlds you are not justified in ruling out plus all the worlds that are not way less plausible than $w$ .

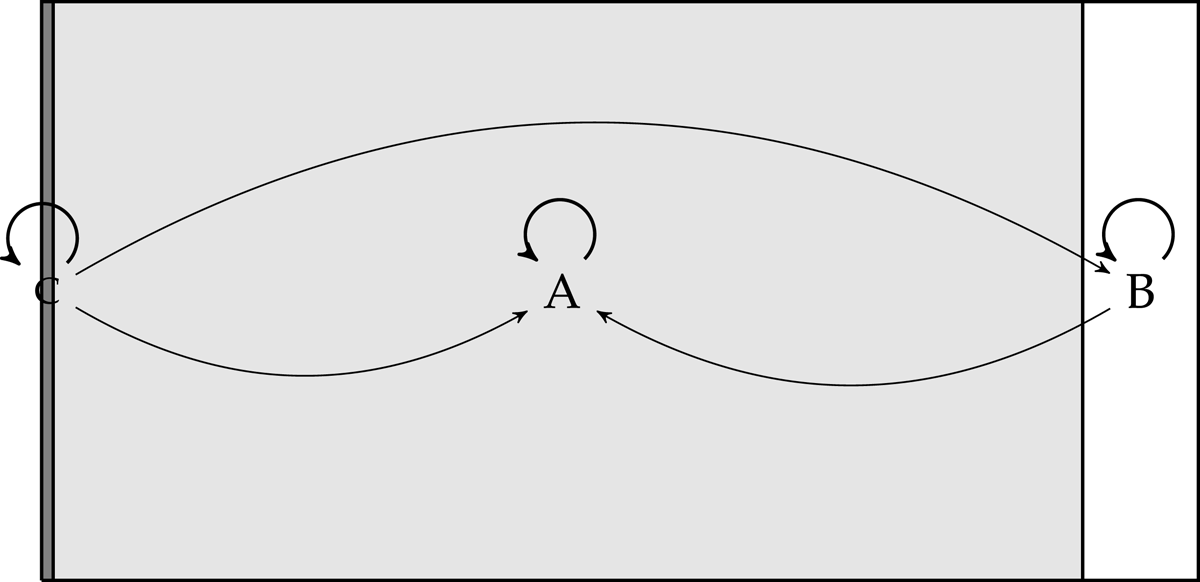
For a graphical illustration, let us return to the case where one is looking at a red wall. As a reminder, (A) The wall is red, (B) The wall is white with trick lighting, (C) One is a BIV and there is no wall. Accordingly, $P r (A) = 0.99$ , $P r (B) = 0.01 − ϵ$ , and $P r (C) = ϵ$ . Fig. 2 below is an illustration to make clear what one knows relative to the question ${A; B; C}$ . In Fig. 2, the arrows show which worlds are epistemically accessible to which other worlds.

Figure 2

Red Wall, White Wall, or BIV? Knowledge

Since $A = R B (w)$ no matter which cell $w$ is in (as we saw in Fig. 1), we know that $A ⊆ R K (w)$ . If $w$ is an A-world, then since the A-worlds are much more plausible than the B-worlds and C-worlds and $P r (A) > 0.91$ , one one can rule out the B-worlds and C-worlds. Thus, in the A-worlds, one can know $A$ . If $w$ is a B-world, then one can only rule out the C-worlds for being too implausible since $P r (B) P r (C) > 10$ . Thus, in the B-worlds, one can know $A ∨ B$ . And finally, if one has the misfortune of being a BIV in a C-world, then one cannot rule out anything, and so one only knows the tautology. In other words, if the wall is red, you know it is red; and if there is trick lighting, you at least know that you aren’t a BIV; and if you are a BIV, you know nothing.

Fortunately, there is an effective procedure one can use to compute $R K (w)$ :

Effective Procedure To Determine $R K (w)$

Add all the worlds in $R B (w)$ to $R K (w)$ .
Find all the cells that are of similar size or bigger than $| w |$ (i.e., cells that are not over ten times smaller than $| w |$ ). Add all the worlds in those cells to $R K (w)$ if they are not already in.
You are done!

Informally, $R K (w)$ is the strongest true answer (or partial answer) to the question that is both probable and much more probable than any of its alternatives.²¹ And depending on the question, what the alternatives are can differ.

Finally, our model is entirely consistent with Closure for both justified belief and knowledge. As is standard, we say that one is in a position to know q at $w$ iff $R K (w) ⊆ q$ . And one is justified in believing $q$ at $w$ iff $R B (w) ⊆ q$ . Thus, if $p ⊆ q$ (i.e., $p$ entails $q$ ), then if one is in a position to know/justifiably believe $p$ , then one is in a position to know/justifiably believe $q$ .

Now that we have our model for knowledge and justified belief, let us return to the Preface Paradoxes.

2.3.2. Applying the Formal Model to the Preface Paradox for Knowledge

Recall that on my view, one can rule out worlds that are much more implausible than the actual world $@$ relative to a certain partition. A world $w$ is much more implausible than the actual world $@$ in the partition ${P; ¬ P}$ when $P r (| @ |) P r (| w |) > 10$ , where $| @ |$ is the cell in the partition of which $@$ is a member, and likewise for $| w |$ .

Thus, on the question, “is $p 1$ true?” (which gives the partition ${p 1; ¬ p 1}$ ) Xin can rule out the worlds where $¬ p 1$ is true since $@ ∈ p 1$ and $P r (p 1) P r (¬ p 1) > 10$ , and so all the $¬ p 1$ -worlds are ruled out. However, relative to this question, Xin cannot rule out any of the worlds where $p 1$ is true. These worlds include worlds where $¬ p 2$ is true, where $¬ p 3$ is true, and so on. Thus, relative to the question “is $p 1$ true?”, Xin can know $p 1$ , but there will be some $¬ p 2$ -worlds that remain uneliminated by Xin’s evidence, and so Xin would not know $p 2$ .

However, in some sense, Xin does “know” $p 2$ ; she just knows it relative to a different question. Relative to the question “is $p 2$ true?”, she can rule out the $¬ p 2$ worlds since $P r (p 2) P r (¬ p 2) > 10$ .

So on this picture, we can accept Combo A. Even more than that, we also picked out what the contextually salient parameter is. So we can rearticulate Combo A as Combo A*:

Combo A*

“Xin knows $p 1$ ” is true relative to the question “is $p 1$ true?”

“Xin knows $p 2$ ” is true relative to the question “is $p 2$ true?”

.

“Xin knows $p n$ ” is true relative to the question “is $p n$ true?”

Furthermore, this picture gives an intuitive reason for why, in many of these contexts, one only knows one proposition (and anything it entails). Since “knowing” is relative to a question, it makes sense to say that Xin knows that $p 1$ is the answer to the question “is $p 1$ true?”, but it doesn’t make sense to say that Xin knows that $p 1$ is the answer to the question “is $p 2$ true?”.

Of course, there can still be contexts where Xin can still know more than one proposition. For example, relative to the question, “is $p 1 ∧ … ∧ p 100$ true?”, Xin can know the answer to that question so long as it is true and $P r (p 1 ∧ … ∧ p 100) P r (¬ (p 1 ∧ … ∧ p 100)) > 10$ (i.e., $P r (p 1 ∧ … ∧ p 100) > 1011$ ).

However, if Xin is not certain in each of $p 1$ through $p n$ , then for sufficiently large $n$ , there will be no context in which Xin can know $p 1 ∧ … ∧ p n$ . This is because we have the restriction that if, after ruling out all the worlds that are much more implausible than the actual world, we are only left with a proposition $P$ s.t. $P r (P) < t$ (where we previously stipulated that $t = 0.91$ ), then we add in the next set of most plausible worlds until the uneliminated possible worlds constitute a proposition $Q$ s.t. $P r (Q) > 0.91$ . The strongest thing one knows relative to that partition, then, is $Q$ . This rule is essentially an instance of the Brand New Rule of Belief, and it ensures that one cannot rule out so many worlds that the set of worlds that are eliminated exceed probability $0.09$ .

With this rule in place, our contextualist picture allows us to both accept Combo A* and reject Combo B, and so we have achieved our desired result.

2.3.3. Question Relative Contextualism and the Original Preface Paradox

The Preface Paradox above is a Preface Paradox for knowledge. What might our contextualist picture say about the original Preface Paradox for justified/rational belief?

Recall that, on our picture, “A is justified in believing $p$ ” is true relative to a particular question. In particular, one is only justified in believing propositions as answers or as partial answers to particular questions. The answer, or partial answer must both be probable (at least over 0.5 probable), and the answer, or each answer within the partial answer, must be way more plausible than any of the alternative answers. With this in mind, let us return to the original Preface Paradox for belief.

The original paradox is presented here:

The Original Preface Paradox

Suppose that in the course of his book a writer makes a great many assertions, which we shall call $s 1, …, s n$ . Given each one of these, he believes that it is true. If he has already written other books, and received corrections from readers and reviewers, he may also believe that not everything he has written in his latest book is true. His approach is eminently rational; he has learnt from experience. The discovery of errors among statements which previously he believed to be true gives him good ground for believing that there are undetected errors in his latest book. However, to say that not everything I assert in this book is true, is to say that at least one statement in this book is false. That is to say that at least one of $s 1, …, s n$ is false, where $s 1, …, s n$ are the statements in the book; that $(s 1, ∧ … ∧ s n)$ is false; that $(s 1, ∧ … ∧ s n)$ is true. The author who writes and believes each of $s 1, …, s n$ and yet in a preface asserts and believes $(s 1, ∧ … ∧ s n)$ is, it appears, behaving very rationally. Yet clearly he is holding logically incompatible beliefs … The man is being rational though inconsistent. (Makinson 1965)

Here, Makinson’s focus is not merely on the author’s beliefs, but on what the author is rational in believing. Note that in this version of the paradox, Closure isn’t even mentioned. This is because the author, though he believes each of $s 1$ through $s n$ , does not believe their conjunction. However, even without Closure, this paradox still reveals an inconsistent triad of plausible principles:

(A) The author rationally believes each of $s 1$ through $s n$ . [We Rationally Believe A Lot]

(B) The author rationally believes $¬ (s 1 ∧ … ∧ s n)$ . [Modesty]

(C) The author cannot rationally believe an inconsistent set of propositions. [Consistency]

Much ink has been spilled in trying to resolve this paradox. For example, many have denied Modesty for various reasons. Some have denied Modesty on the grounds that rational belief is closed under consequence, and so one cannot rationally believe $¬ (s 1 ∧ … ∧ s n)$ because one already rationally believes its negation. Still, some others have denied Consistency (Kyburg 1961), and some have denied it on probabilistic grounds: one can be rational in having a high credence in each of $s 1$ through $s n$ , and thus count as believing each of them, but also be rational in having a high credence in $¬ (s 1 ∧ … ∧ s n)$ (Christensen 2004; Easwaran 2016) and also count as believing it as well.

However, relatively few have questioned We Rationally Believe A Lot.²² Oftentimes, We Rationally Believe A Lot is just stipulated to be true. We are simply told that the author has done the research, and so of course she is justified and rational in believing each of $s 1$ through $s n$ .

But, as we have seen from our contextualist model, We Rationally Believe A Lot should be the assumption to go. For the same reasons for which one can’t know all of $s 1$ through $s n$ in a single context, one also cannot be justified in believing all of $s 1$ through $s n$ either. This is because the conjunction of $s 1$ through $s n$ is too improbable to be believed relative to any question. Thus, there are no contexts in which one can justifiably believe all of $s 1$ through $s n$ . However, for the same reason one can still know each of $s 1$ and $s n$ in different contexts, so also one can rationally believe each of them in different contexts as well.

And so one cannot simply stipulate that one is rational, or justified, in believing each of $s 1$ to $s n$ . But this shouldn’t bother us too much when we accept that most propositions are still believed in some contexts.

The advantage of this solution to the original paradox is that one can also add in Closure for belief without too much worry. For example, if we had chosen to deny Consistency instead, then, by Closure, not only will the author rationally believe an inconsistent set of propositions, the author would also be rational in believing any set of propositions. Thus, those who cling onto Closure are more likely to deny Modesty instead. However, on my contextualist model, Closure and Modesty can get along after all.

2.3.4. Knowing A Lot and Question Sensitive Contextualism

Perhaps one obvious disadvantage of this model is that, although many knowledge ascriptions of the form “Jill knows that $p$ ” are true, so long as Socraticism is true, it would seem that sentences of the form “Jill knows a lot”, or “Jill knows a lot about physics” would be false. It would seem to be a cost of my theory that sentences of that form would come out false since it is sometimes helpful to utter such sentences to point the audience to people who can answer their questions. For example, if I want to learn some physics, and I want to find a teacher, it would be helpful for someone to say, “Go ask Jill. She knows a lot about physics”.

I can perhaps respond to this question in two different ways. The first is to adopt an error-theory and say that sentences of the form “Jill knows a lot” are false; but nonetheless, it is sometimes appropriate to assert something false if it serves some practical purpose.²³ This is a view, although an admittedly costly view. I think a better way to respond is to suggest that sentences of the form “Jill knows a lot” do express a truth in some contexts, but that is not because it expresses the proposition that Jill bears a single knowledge relation that holds between her and a lot of propositions; rather, it is because it expresses the proposition that Jill bears many knowledge relations to each of the many propositions. Let me explain.

Thus far, we have argued that for different contextually salient questions, q, “knows” expresses a different knowledge relation, knows $q$ , that relates a subject, S, and a proposition, p. But context-sensitive expressions have important interactions with quantifiers. For example, the meaning of “local” depends on a contextually determined place; but consider: “Every reporter went to a local bar to hear the news”. This is most naturally understood not as saying that every reporter went to a bar local to the speaker, but rather that they each went to a bar local to them. So the sentence expresses the proposition for all reporters, x, x went to a local $x$ bar to hear the news, where local $q$ is the property of being local to x (example comes from Stanley 2000). The value of the place parameter for “local” varies along with the values that “everyone” ranges over. Context-sensitive expressions typically exhibit this kind of interaction with quantifiers.²⁴ Similarly, in sentences like “Jill knows a lot about physics”, the question parameter for “knows” varies along with the values that “a lot” ranges over. So the sentence “Jill knows a lot about physics” is true whenever it expresses the proposition that for a lot of propositions, $p$ , about physics, Jill knows $p?$ $p$ , where S knows $p?$ $p$ when S knows that $p$ is the answer to the question whether $p$ .

So sentences like “Jill knows a lot about physics”, and even “Xin knows a lot”, exhibit the same features as sentences like “everyone went to a local bar”. And just as sentences like “everyone went to a local bar” has both a true and false reading (depending on whether the place parameter in “local” is coordinated with the quantifier), so too do sentences like “Xin knows a lot” have both a true and false reading (depending on whether the question parameter in “knows” is coordinated with the quantifier). Admittedly, the true reading of “Xin knows a lot” is more natural in common speech. The true reading arises when we are perhaps only concerned with whether we can query Xin for information. In cases like this, we usually want to know whether Xin is the kind of person who knows the answer to a variety of questions, and so the context in which we utter, “Xin knows a lot” does not set the question parameter once and for all, but allows for the question parameter to vary with the proposition variable being bounded.

But not all contexts are like that. At the beginning of this paper, we set up a context in which we asked what Xin can know by deduction. In that context we were concerned with what Xin can know relative to a specific question, since knowledge is only closed under deduction within a question and not across questions. So it is false to say, “Xin knows a lot”, because there is no single knowledge relation that holds between Xin and a lot of propositions. And so in this context, we can truthfully say, “Xin does not know a lot”. There are similar contexts in which we can also truthfully say, “We don’t know a lot”. Indeed, it is in this sense, where the question parameter in “knows” is not coordinated with the quantifier, that we defend the truth of Socraticism.

So much for the contextualist solution to our puzzle. In the following sections, we will explore some non-contextualist solutions. If one is not a contextualist about knowledge, then one who accepts the argument in Section 1 would have to accept Socraticism. Though this view doesn’t quite amount to Skepticism, one might think it’s already bad enough if one can only know about 100 things and forever be left ignorant about everything else. I take it, then, that a non-contextualist would want to rebut the argument. In the following section I will explore non-contextualist solutions that deny No Loss, No Gain.

3. Denying No Loss, No Gain

In this section, we will discuss the views of the “Anti-Socratics”: those who believe Xin Knows A Lot and deny Socraticism. In particular, we will discuss the views of the Anti-Socratics who accept Closure. Anti-Socratics who accept Closure must deny No Loss, No Gain. These Anti-Socratics come in two varieties. The first kind of Anti-Socratic is the one who thinks that Xin knows $p 1$ through $p n$ , but somehow loses some of her knowledge once she learns that there is exactly one false proposition in the book. This kind of Anti-Socratic denies No Loss. The second kind of Anti-Socratic is the one who thinks that, after Xin learns that exactly one of the propositions in the book is false, she can come to know which proposition is false on the basis of deduction. This kind of Anti-Socratic denies No Gain.²⁵

We will discuss the views of the first kind of Anti-Socratic first.

3.1. Denying No Loss by Accepting Strange Defeat

Here we consider the move to deny No Loss. In particular, we are considering the view that Xin starts off knowing every true proposition in the book, but she somehow loses some knowledge the moment she learns that there is exactly one false proposition in the book. On this view, Xin learns something that defeats her previous knowledge. Let us call this phenomena “Strange Defeat”.

The reason why we call this “Strange Defeat” is because the knowledge Xin gains would only defeat her previous knowledge in an unfamiliar way. In familiar cases of defeat, one loses knowledge of $p$ when one learns some other kind of proposition $q$ that somehow undermines one’s confidence in $p$ . For example, suppose Xin had only 3 probabilistically independent beliefs, each with probability $0.99$ . Now, if Xin were told that she had exactly one false belief, Xin’s confidence in each proposition will drop from $0.99$ to roughly $0.67$ (or $23$ ). In this case, it’s not too surprising that Xin would lose knowledge for any one of her true beliefs since she may not even be confident enough to justifiably believe anything anymore. Thus, one’s loss of knowledge can be attributed to one’s loss of confidence. In other words, in familiar cases of defeat, learning some proposition $q$ destroys our knowledge of $p$ partly because $P r (p | q) < P r (p)$ .

But this is not so with Xin. Things are quite different when we have a large number of true beliefs. Suppose for concreteness that Xin had $1000$ probabilistically independent beliefs in her book, and that Xin is $0.99$ confident in each of them. In that case, coming to learn that there is exactly one error in the book would actually raise her confidence in each claim to $0.999$ . So in her case, she has learned some proposition $q$ such that for every proposition $p$ in the book, $P r (p | q) < P r (p)$ ! In Xin’s case, learning that only one of her beliefs is false actually increases her confidence in each of the claims in the book. So if Xin is a victim of Strange Defeat, then she somehow loses her knowledge that $p$ (for some $p$ ) despite learning something that would make her justifiably more confident in $p$ than ever before!

The phenomenon of Strange Defeat would then conflict with the following principle about defeat:

Defeating Evidence Is Not Confirming Evidence (DENCE): If one knows $p$ , then evidence $E$ does not defeat one’s knowledge of $p$ if $P r (p | E) > P r (p)$ .

To see how this principle is inconsistent with the phenomena of Strange Defeat, simply replace $E$ with the proposition $O$ : that there is a single false belief in the book. In that case, if Xin knew every true proposition in the book $p$ , then DENCE implies that she continues to know $p$ when she learns $O$ , since learning $O$ only increases her confidence in each true proposition.

Thus, if one accepts the phenomena of Strange Defeat, then one must say that defeating evidence can be confirming evidence.²⁶

Furthermore, it is hard to see what special reason Xin gains for doubting any of her particular beliefs. At best, the knowledge that exactly one of her beliefs is false might give her some reason to think that, for any particular belief, there is a chance that that belief is the false one. However, it can be argued that Xin already knew that, for any particular belief, there is a chance that that belief is false! It would be strange indeed if the knowledge that one’s belief has a chance of being a false belief does not defeat any knowledge, but the knowledge that one’s belief has a chance of being the only false belief somehow does.

To make this point more vivid, let us imagine that I have many friends who are generally reliable. I ask each of my $1000$ friends whether they can make it to my birthday party. Some say “yes”, and others say “no”, and I come to believe what each of them say. However, even though my friends are incredibly reliable, I know that friends who say “yes” sometimes flake in the end, and friends who say “no” sometimes change their mind. Given the sheer number of friends that I have, I suspect that a few friends would change their minds. So when $500$ of my friends say “yes”, and $500$ say “no”, I estimate that about $500$ , give or take $5$ , people will be at the party.

Now, the Anti-Socratic who denies No Loss would say that, of the truthful friends, I know whether they will show up at the party on the basis of their testimony. However, they would also say that once I learn that only one of my friends will change their mind, I somehow no longer know, for some of my truthful friends, whether they will be at the party. They will say this is so even though I gained no special reason to doubt anyone’s particular testimony (in fact, it increases my confidence in each of my friends)!

I find that conclusion hard to swallow. I find it hard to swallow, for example, to say that I can know that John will be at the party when I know that some friends don’t tell the truth, but that I can’t know that John will be at the party when I know that only one friend did not tell the truth.

Even worse, since this is a case where the basis of my knowledge about each of my friends is the same, it would be arbitrary to say that my knowledge about John is defeated while my knowledge about my other friends remains intact. To avoid this arbitrariness, one would have to say that, once I learn that only one of my friends will change their mind, I cannot know whether any of my friends will change their mind.

Ironically, then, the Anti-Socratic who wishes to salvage We Know A Lot by denying No Loss may have to say that, although we know a lot, we also stand to lose a lot. If even confirming evidence can drive me to doubt the testimony of all my friends, then that would mean that my knowledge is fragile indeed.

Finally, even if the Anti-Socratic who accepts Closure is right in denying No Loss, there is still the problem of how the Anti-Socratic can come to know a lot in the first place. In Xin’s case, it is still puzzling how she can come to know every element of the set $S = {p 1, … p n}$ , and thereby come to know, by Closure, $⋀ S$ . The reason why it is puzzling as to how Xin can come to know $⋀ S$ is because two independent arguments can be made for the conclusion that Xin cannot come to know $⋀ S$ .

Argument from Strong Modesty

(S1) Xin is justified in believing $¬ ⋀ S$ . [Strong Modesty]

(S2) For any proposition $p$ , if one is justified in believing $¬ p$ , then one is not in a position to know $p$ . [Knowledge-Exclusion]²⁷

$∴$ Xin is not in a position to know $⋀ S$

Argument from Weak Modesty

(W1) Xin is not justified in believing $⋀ S$ . [Weak Modesty]

(W2) For any proposition $p$ , if one is not justified in believing $p$ , then one is not in a position to know $p$ . [Knowledge Implies Justification]

$∴$ Xin is not in a position to know $⋀ S$

(S1) and (W1) are plausible for Preface Paradox style reasons—since Xin is not completely certain in each proposition in $S$ , she will be very uncertain in their conjunction (and hence very confident that the conjunction is false).²⁸

(S2) and (W2) are also quite plausible, but not entirely uncontested. We will discuss these two principles more in the next section, but for now it suffices to note their prima facie plausibility.²⁹

Ultimately, any Anti-Socratic who accepts Closure must also deal with the arguments from Strong and Weak Modesty. Thus, even if one accepts the phenomena of Strange Defeat and gives up the principle DENCE, one still needs to say something about (S1) and (S2) and (W1) and (W2). Unless the Anti-Socratic deals also with these two arguments, they cannot explain how Xin can come to know a lot in the first place. Perhaps the Anti-Socratic who denies No Gain can do better. We explore this view in the next section.

3.2. Denying No Gain

In this section, we consider the views of the Anti-Socratic who denies No Gain. Such an Anti-Socratic believes that Xin starts off knowing a lot, continues to know a lot, and comes to even be able to know which of her beliefs is false when told that there is exactly one false proposition in the book.

Anti-Socratics of this sort would also have no problem with the view that Xin is in a position to know $⋀ S$ . After all, if Xin can come to gain the knowledge that $p n + 1$ is false when Xin learns that exactly one proposition in the book is false, it is only because Xin deduces that since $⋀ S$ is true and one of the propositions in the book is false, $p n + 1$ must be the false proposition.

Anti-Socratics who deny No Gain, then, should adopt a principled reason for how Xin can know $⋀ S$ . Doing so would require some principled reason in rejecting either (S1) or (S2) and either (W1) or (W2). Broadly speaking, there are two such strategies for doing so.

The first strategy is to deny both (S1) and (W1) and assert that Xin is in fact justified in believing $⋀ S$ . One way of doing so would be to adopt the E = K thesis (our evidence consists in all and only in what we know). If the Anti-Socratic adopts the E = K thesis, the Anti-Socratic should think that, since Xin knows all the propositions in $S$ , she is justified in being maximally confident in $⋀ S$ , given all her evidence. Thus, Xin would be justified in believing $⋀ S$ (contra (W1)), and Xin would not be justified in believing $¬ ⋀ S$ (contra (S1)).

The second strategy is to deny both (S2) and (W2). To deny (S2) and (W2) would be to assert that someone can know a proposition on insufficient or even on countervailing evidence. As far as I know, Donahue (2019) adopts this strategy. He calls it a variant of Maria Lasonen-Aarnio’s concept of “Unreasonable Knowing”.

Let us first discuss the E = K strategy.

3.2.1. The E = K Strategy

If E = K, the Anti-Socratics can easily identify what is wrong with Strong and Weak Modesty. For since the Anti-Socratic thinks that Xin knows every proposition in $S$ , if they adopt the E = K thesis, then the Anti-Socratic should also think that the probability of $⋀ S$ given everything she knows is 1, and the probability of $¬ ⋀ S$ given everything she knows is 0. Williamson calls our probabilities conditional on everything we know our “Evidential Probabilities”, and so if our credences should match our Evidential Probabilities, we should be certain that $⋀ S$ is true. Now, if our Evidential Probabilities are an indication as to how justified we are in believing a certain proposition, then to have an Evidential Probability of 1 in $⋀ S$ would give us the most justification possible for believing $⋀ S$ . So having an Evidential Probability of 1 in $⋀ S$ would mean that Weak Modesty is false, while having an Evidential Probability of 0 in $¬ ⋀ S$ would mean that Strong Modesty is false.

And once it is clear that one can thereby know $⋀ S$ on the grounds that it has such a high Evidential Probability, it no longer seems so problematic that Xin can simply deduce $¬ p n + 1$ when she learns that exactly one thing she wrote down is false. Furthermore, the E = K view also comes furnished with a candidate explanation for why it is good practice to think that we might be mistaken, even though we know all the propositions in $S$ . The reason is because we often do not $know$ what we know, and so even conditional on everything we know (i.e., $⋀ S$ ) it may still be incredibly improbable that we know $⋀ S$ . In other words, even though $P r (∧ S | ∧ S) = 1$ , $P r (We know ∧ S | ∧ S) < < 1$ . Williamson in fact takes the error-free version of the Preface Paradox to be an example of such “Improbable Knowing” Williamson (2014). And so even though one may be in a position to know $⋀ S$ by deduction, it may be bad practice to believe it on the basis of deduction because such a person who believes the conjunction of a large number of propositions where all of them are known is bound to also believe the conjunction of a large number of propositions where they only seem to be known. So now we have some reason to deny Strong Modesty and Weak Modesty, and we are still able to explain why one should, in some sense, be modest.

I think there is much to like about this view since it vindicates our reliance on Closure but still gives us a candidate explanation for why we find Strong Modesty and Weak Modesty so compelling. However, the E = K view has not gone unchallenged (see Hawthorne 2005; Comesaña & Kantin 2010).

I have at least two general worries for the E = K view. The first worry is that our knowledge goes beyond what we ordinarily take to be our evidence. Hawthorne 2005 gives such an example when he has us consider two cases where a person sees a gas gauge that reads “full”, except in the first case the gauge is accurate while in the second case the gauge is inaccurate. It is intuitive to think that both have the same evidence, but only one knows, and so one can know something that is not part of one’s evidence.

One way to reply to this argument, however, is to contest that the testimonial evidence gained from reading the gauge is only of the form “the gauge reads that…”, or the perceptual evidence that “the gas tank seems full”. In the case where the gauge is accurate, perception and testimony can also give one the proposition that the gas tank is full as evidence. Thus, when the gauge is accurate, one knows that the tank is full because we gain the proposition that the gas tank is full as evidence, but in the latter case, we do not know that the gas tank is full because we only have the proposition that the gas gauge reads “full” as evidence.

However, even if we accept this view of evidence, we can still create other examples where it is intuitive to think that one’s knowledge goes beyond one’s evidence. An example of such a phenomenon comes from the possibility of inductive knowledge. Consider two people in two situations:

Case A:

Anne has observed emeralds $e 1$ through $e 1000$ . Anne doesn’t just learn that emeralds $e 1$ through $e 1000$ look green, but that they are green. On this basis, Anne comes to know that all emeralds are green.

Case B:

Bill has observed emeralds $e 1$ through $e 2000$ . Bill doesn’t just learn that emeralds $e 1$ through $e 2000$ look green, but that they are green. On this basis, Bill comes to know that all emeralds are green.

What shall we say about Anne and Bill? If inductive knowledge is possible, then it is plausible that after Anne has observed 1000 emeralds, she can come to know that all emeralds are green (and if you think 1000 emeralds are too few, feel free to substitute it for a larger number). Bill, however, has observed those same emeralds and 1000 more. So although both Anne and Bill are the same with respect to their knowing whether all emeralds are green, I find it intuitive that Bill has more evidence than Anne does for the proposition that all emeralds are green. Indeed, if Anne later comes to observe the other 1000 emeralds that Bill observed, it would be entirely be appropriate for Anne to exclaim, “ah! more evidence for the fact that all emeralds are green!”.

However, if E = K, then it cannot be the case that Bill has more evidence than Anne because both Bill and Anne $know$ that all emeralds are green, and so the proposition that all emeralds are green is part of both of their evidence. And if the proposition that all emeralds are green are part of both of their evidence, then they both already have the most possible evidence that all emeralds are green, since for every proposition $p$ , $P r (p | p) = 1$ . Thus, Anne could not rationally be more certain than she was before, even if she comes to observe the additional emeralds Bill observed.

Intuitively, however, Bill does have more evidence for the proposition that all emeralds are green than Anne does. If Bill, for example, observed every single emerald in the world, it would be odd to say that Anne has just as much evidence as Bill does for the proposition that all emeralds are green. Furthermore, if Bill (who has seen all emeralds himself, and knows this) hears from a reliable witness (who has seen 5000 emeralds) that all emeralds are green, we would not say that Bill has gained any additional reason for believing that all emeralds are green. If, however, Anne has heard from that same witness that all emeralds are green, we would say that Anne has gained some more evidence that all emeralds are green. But of course, if the proposition that all emeralds are green is already part of Anne’s evidence, then Anne has just as much evidence as if she saw all the emeralds in the world herself, and so hearing from a reliable witness should not give her any additional reason to believe that all emeralds are green at all.

Secondly, on the E = K view, it is hard to justify our practice of sometimes testing hypotheses of which we already know.³⁰ For example, even though one might know that all emeralds are green, it may be worthwhile to gather more emeralds to test this hypothesis. Perhaps we would want to test this hypothesis because, although we know it to be true, we wish to know that we know it, and so further testing may be necessary. However, if we already knew that all emeralds are green, we cannot learn anything more by looking at another green emerald than we could by simply deducing from “all emeralds are green” to “the next emerald I see is green”, or “emeralds $e 1000$ to $e n$ , where $n$ is the number of emeralds, are green”. But if we could simply deduce that all the other emeralds are green from what we know, then going out to search for more evidence that all emeralds are green would be as much of a waste of time as it is for a person to check the weather to see whether it’s true that it is either raining or not raining. Thus, if inductive evidence is possible, and E = K, then all new evidence may just as well be old evidence. And that’s a problem.

3.2.2. The Unreasonable Knowledge Strategy

Another strategy for the Anti-Socratic would be to deny Knowledge-Exclusion and Knowledge Implies Justification. The Anti-Socratic who does this would say that since Xin knows a lot, she can come to know $⋀ S$ , and thereby come to know $¬ p n + 1$ despite the fact that she has insufficient evidence to believe $¬ p n + 1$ and despite the fact that she actually has good reason to believe $p n + 1$ .

Such a move would be quite radical, but such a move has been defended precisely by Donahue (2019).

To see how radical this move is, it would be helpful to distinguish it from the nearby ideas of “Improbable Knowing” and “Level-Splitting”. A case of Improbable Knowing, as mentioned above, is one where one can know $p$ despite the fact that it is highly improbable on one’s evidence that one $knows p$ . However, this move is consistent with both Knowledge-Exclusion and Knowledge Implies Justified Belief. This is because improbable knowing is not a case where one knows $p$ even though $p$ is improbable on one’s evidence—it is only a case where $knowing p$ is improbable on one’s evidence.

Secondly, Knowledge-Exclusion and Knowledge Implies Justification are consistent with the “Level- Splitting” views. The term “Level-Splitting” comes from Lasonen-Aarnio (2014), and it refers to how we should rationally respond to higher-order evidence that suggests that our first-order evidence is somehow unreliable. A paradigm example where one receives such higher-order evidence would be a case where one sees a red wall, comes to gain perceptual evidence that the wall is red, but is then (misleadingly) told by a usually reliable friend that one has just ingested a drug that makes it seem like white walls are actually red. In such a case, a “Level-Splitter” would be one who would say it is rational to believe that the wall is red based on one’s first-order perceptual evidence about the redness of the wall, but also believe (based on the higher-order testimonial evidence) that one does not have sufficient evidence to justifiably believe that the wall is red.

Such a view has some odd consequences (see Horowitz 2014 for examples of such consequences), but not even the level-splitter has to deny either Knowledge-Exclusion or Knowledge Implies Justification. The level-splitter only needs to say that one’s evidence $E$ can support $p$ , but one’s higher-order evidence $HE$ can cast doubt on whether $E$ supports $p$ . But since, on the level-splitting view, higher-order evidence does not decrease one’s rational credence for $p$ , one’s total evidence simply supports $p$ . Thus, even the level-splitter does not have any reason to think that one can know $p$ even if one has insufficient evidence for, or even countervailing evidence against, $p$ .

For an example where something like Knowledge-Exclusion is false, we need a case where one is justified in believing $¬ p$ , but where one can knows $p$ nonetheless. Sean Donahue thinks that the Preface Paradox for knowledge is precisely an example of this kind of case. Donahue has us consider a variant of the Preface Paradox where an agent in fact knows all the claims in her book. Since knowledge is closed under deduction, the agent comes to know the conjunction of all the claims in the book. Nonetheless, she has excellent inductive evidence (based on all the errors she discovered in her previous books) that the conjunction is false. So she can know that the conjunction is true, although she is justified (by her inductive evidence) that the conjunction is false. Thus, we supposedly have an example where Knowledge-Exclusion fails.

Furthermore, in order for this example to work, it also needs to be a case where Knowledge Implies Justified Belief fails. This is because, if knowledge implies justified belief, then if an agent knows the conjunction, she would also be justified in believing in the conjunction. But the counter-example crucially relies on the intuition that the agent is justified in believing the negation of the conjunction. Of course, it is possible for the agent to be justified on one basis in believing the conjunction, and justified on another basis in believing its negation; but we are interested in what the agent is justified in believing in full stop. To answer this question, we need to know what the agent is justified in believing on the basis of one’s total evidence. So if the agent is justified in believing in the negation of the conjunction on her total evidence, she cannot be justified in believing the conjunction. This is because to the degree that one is justified in believing a proposition $p$ , one should also be justified to the same degree in disbelieving $¬ p$ . On the probabilistic framework which we are working in, this is unavoidable since the higher $P r (p | E)$ is, the lower $P r (¬ p | E)$ must be. Thus, if $P r (¬ p | E)$ is high enough to justify believing in $¬ p$ , then $P r (p | E)$ cannot be equally as high so as to justify believing $p$ (assuming, of course, that one can only be justified in believing $p$ when $P r (p | E)$ is at least greater than 0.5).

Thus, if Donahue’s variant of the Preface Paradox is a genuine counter-example to Knowledge-Exclusion, it must also be a counterexample to Knowledge Implies Justification. But if this variant really is a counter-example to these two principles, what explains their plausibility? What, for example, explains our intuitive judgment that an agent cannot know the conjunction on insufficient evidence, and in this case, countervailing evidence?

Donahue explains this intuition by noting that though Knowledge-Exclusion (and perhaps by extension, Knowledge Implies Justified Belief) is false, there is still something blameworthy about an agent who goes ahead and believes in the conjunction of all the claims in her book. In particular, such an agent would be blameworthy because she is not manifesting knowledge-conducive dispositions. Being inspired by Lasonen-Aarnio, Donahue treats the Preface Paradox as just another instance of “Unreasonable Knowing” where one can know a proposition $p$ although one is unreasonable for believing $p$ because one would be manifesting a non-knowledge-conducive disposition in doing so. In this case, it is unreasonable for an agent to believe the conjunction because it manifests the disposition to believe the conjunction of claims that seem to be known. And of course, an agent cannot always distinguish cases where claims are known and where they only seem to be known, and so to manifest a disposition to believe a conjunction of claims that seem to be known is bound to lead one into error in the majority of cases where the conjunction is large enough. However, Donahue is quick to note that though an agent would be unreasonable in this sense for believing the conjunction, this by no means shows that the agent does not thereby obtain knowledge through these unreasonable means.

However, I think this strategy goes too far. If we can explain away our intuition that an agent cannot know something on insufficient, and even on countervailing evidence, by appealing to Donahue’s take on Unreasonable Knowing, then we can explain away almost any of our intuitions where we think true belief falls short of knowledge. For example, intuitively, if Jack believes that the number of stars is odd because he likes odd numbers, then Jack does not know that the number of stars is odd, even if its true. However, if Donahue is right, then we could easily explain away this intuition by saying that Jack does know that the number of stars is odd, however, he is still epistemically blameworthy because he is not manifesting knowledge-conducive dispositions. Likewise, if Jack believes that the number of stars is odd despite overwhelming evidence that it is not, we can similarly explain away our intuition that Jack doesn’t know by saying that Jack is still epistemically blameworthy because he is not manifesting knowledge-conducive dispositions.

Here, Donahue may reply that in the examples I gave, an agent has a true belief on no evidence, while in the Preface case, the agent knows the conjunction because she deduces it from known premises. Thus, the agent in the Preface case still has some evidence for believing the conjunction.

However, whether or not an agent has some evidence is beyond the point. After all, one would not say that Jack still gets to know that the number of stars is odd on the basis of an unreliable news source just because Jack has some evidence. Likewise, if Jack had some evidence that the number of stars is odd, but is also swamped by overwhelming evidence that it is not, one would also say that Jack does not have knowledge.

Perhaps this is just what the Anti-Socratic wants to say. The Anti-Socratic wants to say that we know a lot. One way of securing this is to make knowledge a ridiculously easy epistemic state to achieve. Denying Knowledge-Exclusion and Knowledge Implies Justification does just this. However, for Anti-Socratics who think that knowledge must be something more than just true belief, denying these two principles may just be too heavy a cost.

4. Conclusion

The common sense view is that we know a lot. In this paper, I hope to have shown through a variant of the Preface Paradox that we, in fact, do not know very much. However, though I have argued that this common sense view is false, I still maintain the common sense view that many of our knowledge-ascriptions are true. In order to secure the truth of many of our knowledge ascriptions, I needed a contextualist view where one can only know relatively few things in a certain context. My contextualist view that treats knowledge as relative to a contextually provided question does just this.

However, for the Anti-Socratic, it isn’t enough that many of our knowledge ascriptions are true. They really want it to be true that we do know as much as we think we know in any given context. This common sense view turns out to be fairly costly. Either the Anti-Socratic must give up Closure, or they must give up No Gain, No Loss. Giving up either of those principles, however, can lead us to highly unintuitive consequences.

That being said, there are some pressing questions that the Question-Sensitive Contextualist must answer. For example, what are the rules and mechanisms that govern context shift? Where do bread and butter epistemological notions such as safety and reliability fit into our picture? Do those notions play a role in determining which contexts are active, or will they fall by the wayside? These questions have been raised, but they must be left for further research.

Notes

Quote from Lewis (1996). ⮭
Indeed, some of the most common explanations for why we intuitively do not think that one can know whether any particular lottery ticket will lose simply do not apply in Xin’s case. For example, some authors think that we cannot know whether any particular ticket will lose because our evidence for thinking so is (a) perfectly symmetrical (Christensen 2004 cites BonJour 1985, Ryan 1996, Evnine 1999 for a similar view), or (b) purely statistical Cohen (1988). However, in Xin’s case, neither (a) nor (b) hold. ⮭
Alternatively, the E = K theorist may argue that the case as I described it is impossible. The E = K theorist may be convinced that, since we stipulated that Xin has evidence par excellence for each of her true beliefs, she really does know each of them. In that case, on the E = K view, it would be impossible for Xin to rationally be extremely confident that she has at least one false belief. In fact, she should be extremely confident that she has no false beliefs. I consider this view in Section 3.2, and I directly deal with the E = K view in Section 3.2.1. ⮭
For the purposes of this paper, I think we can rest content with an informal understanding of what it means for propositions to “not be too dependent on each other”. For example, the propositions in a book, the propositions I write on a long test, and the propositions I’ve come to believe in the last week are all clearly probabilistically dependent on each other, but they are still not so dependent on each other that the probability of their conjunctions is not much lower than the probability of their most probable conjunct. Essentially, the qualifier that a set of propositions be “not too dependent” on each other rules out cases where having a high credence in just a few of the propositions in a large set would lead to having a high credence in the conjunction of all the propositions in that set. ⮭
I find Closure to be a feature of the view I will argue for, but I am aware that not all will want Closure to be true (see Nozick 1981; Dretske 1970). To those who wish to deny Closure, I recommend that they should treat this paper as more of an exploration of how a person who wishes to accept Closure may deal with the puzzle at hand. I hope such an exploration would be interesting in its own right. ⮭
Strictly speaking, the contextualists will be defending a Closure Schema, where there is one instance of the schema for each relation $know s i$ for every $i$ . In the following, we will just use the term Closure to refer to whichever instance of the schema is relevant. ⮭
In the following, I will sometimes say that an agent knows something in some context but not in another. I hope to make it clear that when I use this locution, I am playing fast and loose with the use and mention distinction for convenience sake. Officially, when I say that an agent $A$ knows $p$ in context $c$ , I mean that the sentence “ $A$ knows $p$ ” is true relative to context $c$ . ⮭
Here we discuss a contextualist view where rational credence above a threshold is sufficient for knowing a true proposition (where the threshold is context sensitive). A stronger version of this view would be one where confidence above a threshold would be both sufficient and necessary. However, on this particular view, we have the result that Xin also cannot $kno w low$ $¬ p n + 1$ since Xin is not even $0.9$ certain in $¬ p n + 1$ . So we would also have an inconsistency here. ⮭
Here I am implicitly relying on a principle called Knowledge Exclusion whereby, roughly, one cannot be in a position to know $p$ if one believes $¬ p$ . In Section 3.2.2 I defend this principle against some objections. ⮭
Strictly speaking, Lewis speaks in terms of “eliminating” a possibility, where a possibility is eliminated when one’s having of an experience is incompatible with that possibility obtaining (1996: 553). Given our Fallibilist commitments, talk about having an experience that is incompatible with a possibility is too strong. Instead, we will talk in more general terms of “ruling out” a possibility, where a possibility may be ruled out if one has sufficiently good evidence that it does not obtain. ⮭
Indeed, Lewis himself recognizes that “salient resemblance” is context sensitive, and so he admits that there are even contexts in which we can know that a person will lose the lottery because the worlds where that person wins the lottery does not saliently resemble actuality in that context. Lewis gives the example of poor Bill to demonstrate such a context: “Pity poor Bill! He squanders all his spare cash on the pokies, the races, and the lottery. He will be a wage slave all his days. We know he will never be rich” (1996: 565). ⮭
Here I do not want to suggest that Lewis’s contextualism has no resources for showing how we cannot rule out the possibilities we are not properly ignoring. Indeed, Lewis’s talk of “eliminating possibilities” may be strong enough to show that if we are not properly ignoring the possibility that Xin’s friend emailed a random text generator, we simply cannot know that she didn’t (even as Xin is repeatedly running the Hamlet program). This is because Xin’s experience of observing the program produce all of Hamlet is still consistent with the possibility where her friend sent her a random text generator that produced all of Hamlet every time. On this view, perhaps the New Rule of Belief does entail that one can know relatively few things per context. However, I find that talk of terms of “elimination” may be too strong. There are many possibilities that I take to be left uneliminated by my evidence; nonetheless, I still know those possibilities to not obtain. The same goes for you. For example, if I tell you here that this entire paper was actually written by a random word generator, you will have to admit that your experience of reading this paper does not eliminate that possibility. However, as I mention the possibility, I take it that you can correctly ascertain that I am joking, and that I have not in fact used a random word generator. A die-hard Lewisian might say that, in fact, after I raised this possibility, you no longer know that this paper was written by human hands. Such a conclusion would be quite extreme. I think that if we can achieve the results we need without having to resort to such extremes, then that would be a plus. In the next section, I attempt to do just that. ⮭
A Boolean $Σ$ -Algebra over $W$ is just a set of subsets of $W$ that (i) contains $W$ itself, (ii) is closed under complement (i.e., if $A$ is in $ℬ$ , then $A$ is in $ℬ$ ), and (iii) is closed under countable union (i.e., if $A 1$ , $A 2$ , … $A i$ , … are all in $ℬ$ , then ⋃_i A_i is in $ℬ$ ). For simplicity, we can simply let $ℬ$ be $P (W)$ . Nothing much turns on that simplification. ⮭
Alternatively, we can define >> with primitive conditional probabilities like so: $w > > w ′$ iff $P r (| w | | | w | ∪ | w ′ |) < t$ . ⮭
The plausibility relation given here is the same one that Lin and Kelly (2012) give. In that paper, they define the plausibility relation like so in order to define an acceptance condition for propositions. Their acceptance condition will be similar to clause 1 of my recursive definition for my doxastic accessibility relation in the next section. Goodman and Salow (2021) have also independently developed a very similar model of knowledge and belief to our own. See also Goodman and Salow (in press) for further discussion and developments of this view. Holguín (in press) has also independently developed a comparable view for rational belief to account for the preface and lottery paradoxes for belief. ⮭
Strictly speaking, this is a definition of $R P B (w)$ where the belief relation $R B$ is relativized to the partition $P$ . For ease of readability, I have omitted the subscript $P$ when it is clear which partition we are talking about. ⮭
This example comes from Jonathan Wright (2018) Our redefined doxastic accessibility relation will follow a solution that is close to his. I should note, however, that the view that we can rationally believe extremely improbable propositions has been recently defended by Dorst and Mandelkern (in press), Dorst (2019), and Holguín (in press). These philosophers will not see any need to revise Definition 2. ⮭
For ease of exposition, we can just let the threshold $t$ be between $0.5$ and $1$ ; but in fact, we would like some more constraints on what $t$ should be. For example, at the very least, $t$ should be the threshold required for believing $p$ under the question “is $p$ true?”. Since we stipulated that one can believe $p$ under the question “is $p$ true?” when $P r (p) P r (¬ p) > 10$ , this makes is the case that $t > 1011 ≈ 0.91$ . This requirement is most obviously needed when we think about knowledge. Without it, we can get absurd results where one fails to know whether it is raining (because Pr(rain) = 0.51), but one can know whether it is raining, snowing, sunny, hailing, etc…(because the probability of any particular weather condition other than rain is far less than $0.51$ ). ⮭
In the case where the strongest probable answer is just a partial answer, what matters is that each cell in the partial answer is much more probable than all the other alternatives not in the partial answer. ⮭
This definition for the epistemic accessibility relation is similar to the one presented in a footnote in Goodman and Salow’s paper, “Taking A Chance On KK” (2018). ⮭
In the case where the strongest true probable answer is just a partial answer, what matters is that each cell in the partial answer is much more probable than all the other alternatives not in the partial answer. ⮭
One prominent exception may be Leitgeb (2014) who argues that, in most contexts, one only believes that most of $s 1$ through $s n$ is true, and in other contexts, one only believes that one of them is true. This solution is similar to mine, except Leitgeb is aiming to explain what an author believes or asserts when writing a whole book, not what an author rationally believes or asserts. Indeed, Leitgeb thinks that, in some contexts, one can indeed double down and assert that everything one has written in the book is true. Whether this is irrational, or unjustified, is not discussed in his short piece. ⮭
This move is akin to a pragmatic approach to quantifier domain restriction. On that view, sentences like “every bottle is in the room” always quantifies over every bottle in the universe, and will almost always come out false in every context. Nonetheless, even in asserting this falsehood, a truth is communicated via implicature—i.e., that every bottle in the house (for example) is in the room. ⮭
For example, context sensitive expressions like “exactly one” and paradigmatically context-sensitive adjectives like “tall” all exhibit this kind of interaction with quantifiers. Consider an example adapted from Stanley and Szabó (2000): “In most of John’s classes, he fails exactly one Frenchman”. The natural way of interpreting the domain of the quantifier “exactly one Frenchman” is to interpret it as varying with the values of the quantifier “most of John’s classes”. So we can understand the statement as saying, “In most of John’s classes, x, there is exactly one y in D $x$ , such that John fails y”, where D $x$ is the quantifier domain that varies with the class x. Similar things can be said of the sentence, “In some places, our six-foot friend is tall, and in other places he is not”. This sentence expresses the proposition there is a place x and a place y such that our six-foot friend is tall $x$ but not tall $y$ , where tall $x$ is the property of being tall compared to people living in $x$ and tall $y$ is the property of being tall compared to people living in $y$ . ⮭
Theoretically, there can be a third kind of Anti-Socratic who accepts No Loss, No Gain and Closure, but denies Xin is Fallible. However, I take it that Xin is Fallible is unassailable—there is no reason to think that we cannot assume that there is a proposition that Xin falsely believes, and hence, does not know. Thus, we will be ignoring this kind of Anti-Socratic. ⮭
Some views seem to imply the possibility of Strange Defeat. For example, Nagel (2011) has argued that one can destroy someone’s knowledge of who the Pope is by citing to them the fact that people of Pope Francis’s demographic have a $0.9999918384$ chance of dying from a heart attack. She then argues that the reason that learning such a fact might destroy one’s knowledge need not be because it reduces one’s confidence in the proposition that the current Pope is Francis (presumably, this new evidence can even raise one’s confidence); rather, learning this fact can destroy one’s knowledge because one has now shifted from the unreflective System 1 thinking to the more reflective System 2 thinking such that under this mode of thinking, one can no longer access one’s prior knowledge in occurrent judgment. However, Nagel is also careful to note that it is compatible with her view to say that one knows who the Pope is all along, although learning new information may simply put us in a mode of thinking that make it difficult for us to register ourselves as knowing who the Pope is. ⮭
The term “Knowledge-Exclusion” comes from Donahue (2019). The principle we call “Knowledge-Exclusion” here is actually a close variant of what Donahue calls “Rational Knowledge-Exclusion”. ⮭
In the original Preface Paradox, Makinson (1965) gives inductive reasons for why someone like Xin shouldn’t be believe $⋀ S$ . The reason is that, since there has always been at least one error in every book she wrote, she should believe that this book of hers has at least one error too. ⮭
It is also worth noting that the contextualist model presented in Section 2 vindicates both (S2) and (W2). Our model implies (S2) since we have as a necessary condition for both knowledge and belief in $p$ that $P r (p) > t > 0.5$ . Thus, if one is justified in believing $¬ p$ , then $P r (¬ p) > 0.5$ , and thus $P r (p) < 0.5$ , and so one cannot be in a position to know $p$ . Our model also implies (W2). This can easily be seen when we recall that our definition for the epistemic accessibility relation $R K$ can be expressed in terms of our doxastic accessibility relation $R B$ like so:
Definition 5. $R K (w) = R B (w) ∪ {w ′ : ¬ (w > > w ′)}$
Thus, it can be clearly seen that any doxastically accessible world is also epistemically accessible, and so knowledge implies justified belief. So our contextualist model has the added benefit of implying these two plausible principles. Needless to say, the model implies both Modesty principles as well, as was discussed in the last section. ⮭
Nado (2019) gives a particularly vivid example of this in the history of medicine—in 1947, aspirin was already widely prescribed by doctors because of its known effects on alleviating pain and fevers. Nonetheless, doctors knew this even before 1948 when the first results of a randomized control trial of a medication was published (Bhatt 2010). ⮭

Acknowledgements

Many thanks to Andrew Bacon, Jeremy Goodman, John Hawthorne, Jeff Russell, and two anonymous referees for their valuable feedback. Thanks also to the audience of the 12th annual Arché Graduate Conference, and special thanks to my commentator, Paolo Savino. Special thanks also goes to Andrew Bacon and Jeff Russell for their extensive feedback on multiple drafts.

References

1 Benton, Matthew A. (2017). Lotteries and Prefaces. In Jonathan Jenkins Ichikawa (Ed.), The Routledge Handbook of Epistemic Contextualism (168–76). Routledge.

2 Bhatt, Arun (2010). Evolution of Clinical Research. Perspectives in Clinical Research, 1(1), 6–10.

3 BonJour, Laurence (1985). The Structure of Empirical Knowledge. Harvard University Press.

4 Christensen, David (2004). Putting Logic in Its Place: Formal Constraints on Rational Belief. Oxford University Press.

5 Cohen, Stewart (1988). How to Be a Fallibilist. Philosophical Perspectives, 2, 91–123. http://doi.org/10.2307/2214070

6 Comesaña, Juan and Holly Kantin (2010). Is Evidence Knowledge? Philosophy and Phenomenological Research, 80(2), 447–54. http://doi.org/10.1111/j.1933-1592.2010.00323.x

7 DeRose, Keith (2009). The Case for Contextualism: Knowledge, Skepticism, and Context (Vol. 1). Oxford University Press.

8 Donahue, Sean (2019). Knowledge Exclusion and the Rationality of Belief. Analysis, 79(3), 402–10.

9 Dorst, Kevin (2019). Lockeans Maximize Expected Accuracy. Mind, 128(509), 175–211. http://doi.org/10.1093/mind/fzx028

10 Dorst, Kevin and Matthew Mandelkern (in press). Good Guesses. Philosophy and Phenomenological Research. http://doi.org/10.1111/phpr.12831

11 Dretske, Fred I. (1970). Epistemic Operators. Journal of Philosophy, 67(24), 1007–23. http://doi.org/10.2307/2024710

12 Easwaran, Kenny (2016). Dr. Truthlove Or: How I Learned to Stop Worrying and Love Bayesian Probabilities. Noûs, 50(4), 816–53. http://doi.org/10.1111/nous.12099

13 Evnine, Simon J. (1999). Believing Conjunctions. Synthese, 118(2), 201–27. http://doi.org/10.1023/A:1005114419965

14 Goodman, Jeremy and Bernhard Salow (2018). Taking a Chance on KK. Philosophical Studies, 175(1), 183–96. http://doi.org/10.1007/s11098-017-0861-1

15 Goodman, Jeremy and Bernhard Salow (2021). Knowledge from Probability. In Joseph Y. Halpern and Andres Perea (Eds.), Theoretical Aspects of Rationality and Knowledge TARK (2021) (171–86). Oxford University Press.

16 Goodman, Jeremy and Bernhard Salow (in press). Epistemology Normalized. Philosophical Review.

17 Groenendijk, Joroen and Martin Stokhof (1984). Questions. Handbook of Logic and Language, 10(2), 1059–131.

18 Hawthorne, John (2002). Lewis, the Lottery and the Preface. Analysis, 62(3), 242–51. http://doi.org/10.1111/1467-8284.00363

19 Hawthorne, John (2003). Knowledge and Lotteries. Oxford University Press.

20 Hawthorne, John (2005). Knowledge and Evidence. Philosophy and Phenomenological Research, 70(2), 452–58. http://doi.org/10.1111/j.1933-1592.2005.tb00540.x

21 Holguín, Ben (in press). Thinking, Guessing, and Believing. Philosophers’ Imprint.

22 Horowitz, Sophie (2014). Epistemic Akrasia. Noûs, 48(4), 718–44. http://doi.org/10.1111/nous.12026

23 Kyburg, Henry E., Jr. (1961). Probability and the Logic of Rational Belief. Wesleyan University Press.

24 Lasonen-Aarnio, Maria (2014). Higher-Order Evidence and the Limits of Defeat. Philosophy and Phenomenological Research, 88(2), 314–45. http://doi.org/10.1111/phpr.12090

25 Leitgeb, Hannes (2014). A Way Out of the Preface Paradox? Analysis, 74(1), 11–15.

26 Lewis, David (1996). Elusive Knowledge. Australasian Journal of Philosophy, 74(4), 549–67.

27 Lin, Hanti and Kevin Kelly (2012). Propositional Reasoning That Tracks Probabilistic Reasoning. Journal of Philosophical Logic, 41(6), 957–81.

28 Makinson, D. C. (1965). The Paradox of the Preface. Analysis, 25(6), 205–7.

29 Nado, Jennifer (2019). Who Wants to Know? In Tamar Szabo Gendler and John Hawthorne (Eds.), Oxford Studies in Epistemology Volume 6 (114–136). Oxford University Press. http://doi.org/10.1093/oso/9780198833314.003.0005

30 Nagel, Jennifer (2011). The Psychological Basis of the Harman-Vogel Paradox. Philosophers’ Imprint, 11(5), 1–28.

31 Nozick, Robert (1981). Philosophical Explanations. Harvard University Press.

32 Ryan, Sharon (1996). The Epistemic Virtues of Consistency. Synthese, 109(2), 121–41. http://doi.org/10.1007/bf00413765

33 Stanley, Jason (2000). Context and Logical Form. Linguistics and Philosophy, 23(4), 391–434. http://doi.org/10.1023/A:1005599312747

34 Stanley, Jason and Zoltán Gendler Szabó (2000). On Quantifier Domain Restriction. Mind and Language, 15(2–3), 219–61. http://doi.org/10.1111/1468-0017.00130

35 Unger, Peter (1971). A Defense of Skepticism. Philosophical Review, 80(2), 198–219. http://doi.org/10.2307/2184030

36 Williamson, Timothy (2000). Knowledge and Its Limits. Oxford University Press.

37 Williamson, Timothy (2014). Very Improbable Knowing. Erkenntnis, 79(5), 971–99.

38 Wright, Jonathan (2018). Rigged Lotteries: A Diachronic Problem for Reducing Belief to Credence. Synthese, 195(3), 1355–73. http://doi.org/10.1007/s11229-016-1275-x

39 Yablo, Stephen (2014). Aboutness. Princeton University Press.

40 Yalcin, Seth (2018). Belief as Question-Sensitive. Philosophy and Phenomenological Research, 97(1), 23–47. http://doi.org/10.1111/phpr.12330