Individuating Powers: On the Regress/Circularity Individuation Arguments against Bird’s Dispositional Monism

1. Introduction

According to Bird’s Dispositional Monism (DM), all properties are essentially dispositional (synonymously, powers).¹ Lowe has challenged the position, claiming that

[i]f all properties were powers, then all manifestations of powers—being properties of their bearers—would themselves be powers, likewise ‘getting their identity’ from their manifestations. […] The problem […] is that no property can get its identity fixed, because each property owes its identity to another, which in turn owes its identity to yet another—and so on and on, in a way that, very plausibly, generates either a vicious infinite regress or a vicious circle. (2006: 138)

Lowe’s intended way out is to posit non-powers to break the regress/circularity. Bird (2007b) conceded the difficulty for the position (he also agreed with Lowe on the crucial premise that a power’s manifestation is itself a property, and so a power; I will too); he then performed a structuralist side-step, claiming that powers’ identities are not simply fixed by their manifestations, but by the overall structure generated by the manifestation-relation, pairing each power to its manifestation; Bird has asymmetric structures in mind, viz., structures without non-trivial automorphisms, in which structural information is sufficient to uniquely characterize any object in it. Lowe (2010; 2012) has then replied, further elaborating his objection.

The Bird-Lowe debate has recently enjoyed a small but intense surge of interest, and while someone was satisfied by Bird’s strategy (Barker 2009: 243), the majority agreed that the so-called “identity regress argument” was too coarsely characterized to be properly resolved; most importantly, a crucial ambiguity in the use of “identity” was noted.² Busse (2021) has successfully shown that, given a model-theoretic reconstruction of Bird’s claim, the numerical distinctnesses of the objects in a structure are indeed entailed by its asymmetric relational pattern; however, as Busse notices, it is unclear whether the identity of a power—in the non-relational sense of its nature or essence—might be so relationally or structurally determined, as Bird (2007b: 524) has claimed. A power’s nature may be determined by its manifestation, in turn another power, which itself needs another power to have its nature determined—eventually leading to a “nature regress”, as in Ingthorsson (2015); alternatively, first-order powers may have their natures determined holistically by second-order structures which they themselves are part of. An air of circularity looms over both scenarios, one in which powers unavoidably need other powers, and themselves, to have some reality or being.³

In this paper, I will rather focus on the identity regress argument as an individuation circularity/regress argument against Bird’s DM. To be sure, many of these identity regresses are closely related to one another, and the resolution of one may very well translate to a solution for another; this is especially true for many non-relational readings of “identity”; for example, in the case of individuation regresses and essence-based regresses. At any rate, the topic of essentialism is too broad to be exhaustively discussed here, and although much of what I will say in these pages has a bearing on issues such as Ingthorsson’s “nature regress”, here I will primarily focus on the claim that DM generates a regress or circularity in metaphysical individuation, as explicitly claimed in Lowe (2010; 2012). According to Bird (2007a: ch. 4), DM entails that powers are individuated by their manifestations, so the charge would appear to stick; yet Bird has never explicitly dealt with the identity regress argument as concerning individuation, so this paper is not meant to provide any exegetically faithful reconstruction of Bird’s stance. I will call the conjunction of DM and the claim that powers are individuated by their manifestations, Naïve DM; while the conjunction of DM and the claim that powers are individuated by their structures, I will call Structuralist DM. While Structuralist DM is supposedly a way out from the individuation problems of Naïve DM, it has been argued to be just as problematic, if not more so. The prospects for Bird’s DM as a whole, then, would appear to be slim.

I think that such concerns are greatly exaggerated; but to reach this conclusion, a better understanding of metaphysical individuation is needed. In the next section I will introduce the topic of individuation, and Lowe’s charge against Naïve DM. In Section 3, Structuralist DM and its problems will be delineated. I will then articulate my solution to the problem: in Section 4 I will argue that while, following Lowe’s stance, metaphysical individuation has often been characterized as a binary relation between objects, a different approach is preferable, which will tentatively lead to a characterization of individuation as a standard explanatory relation between facts; and a new principle of metaphysical individuation for powers in terms of their manifestations will be laid out. This understanding of individuation lifts Naïve DM of all charges. In Section 5, an alternative conception of metaphysical individuation as a sui generis explanatory relation will be explored, which supports Lowe’s original argument against Naïve DM. Yet, under that alternative conception, Structuralist DM has the tools to solve all the problems previously raised against it. Finally, some further difficulties against Structuralist DM will be dispelled, and Section 6 will offer some concluding remarks.

Notably, I will not decide between these two conceptions of metaphysical individuation, viz., as a standard or sui generis explanatory relation; but since only Structuralist DM can deal with the individuation-based circularities and regresses formulated through both the standard the sui generis kind, it is perhaps to be crowned as the best option, thus cementing the validity of Bird’s structuralist side-step. All in all, this is sufficient to prove that DM is significantly less endangered from individuation circularities—and Lowe’s intended way out (viz., to add non-powers) loses much of its initial appeal.

2. The Individuation Circularity/Regress against Naïve DM

There is an epistemic phenomenon that we might call “individuation”, more aptly an operation one can perform: when something is individuated (by an agent) it is singled out from its environment; it is selected, amongst others of a kind, as a distinct subject of focus, perception, or thought. There is however a metaphysical phenomenon which underpins this kind of operation, as there must be something allowing objects to be (epistemically) individuated:⁴ they must be individuals. Not all objects are individuals: but each individual is the very individual it is, rather than another, and thus is distinct from others of the same kind. In a collection of individuals there is always a fact of the matter as to which is which. Thus individuals can, at least in theory, always be individuated (in the epistemic sense). We now encounter the relation of metaphysical individuation of objects of a kind K, which is the proper subject matter of this paper: some x of a given kind K is metaphysically individuated in the sense that something (its individuator) makes it the very K it is, instead of another—and thus makes it an individual. Lowe (2012: 215) famously characterized metaphysical individuation as a binary relation of identity-dependence between objects.

Powers, supposedly, are individuals. With this simple background in mind, we can see an individuation regress/circularity concerning Naïve DM. For simplicity, let us ignore the role of stimuli, and the possibility of multi-track powers, viz., powers with more than one manifestation (as in Bird 2007b: 529—but we will come back to multi-track). If manifestations are properties and thus powers, each power is individuated by another power, producing either an infinite regress (if properties are infinite in number), or a circularity (if they are not). One might wonder why such an infinite regress or circularity is vicious, to which Lowe submits:

[t]wo different entities of the same kind cannot both individuate each other any more than—to use the memorable analogy exploited by Russell—two people can make a living by taking in each other’s washing. […] Consider first the two-entity case. Two distinct Ks cannot each determine which K the other one is, because unless it is already determined which K one of them is, this K cannot fix the identity of the other. And the two-entity case surely generalizes. (2010: 21)

Unfortunately, Lowe doesn’t elaborate; perhaps the thought is that since the asymmetry of metaphysical individuation is motivated by the inadmissibility of circular explanations (Lowe 2012: 215), transitivity is required as well as asymmetry. In the case of an infinite regress what matters is that individuation is well-founded.

This is where we can learn a little bit more about metaphysical individuation as identity-dependence; according to Lowe (2012: 215) such a relation is a kind of “in virtue of” non-causal explanation, which is “metaphysical—rather than the merely epistemic”. Should we take it to be a form of (metaphysical) grounding? We may as well. In my opinion, not much hinges on this decision: in this context the grounding terminology may be more harmless than it sounds, given that our grasp on metaphysical grounding, especially formal features such as asymmetry and transitivity (those needed to get Lowe’s argument going) crucially depend on the association between grounding and explanation, as in Raven (2013: 193–94) and Maurin (2019).⁵ Non-causal explanation, perhaps metaphysical explanation (if there is such a thing), is the minimal notion that we need here; one is then free to enrich it with a grounding element, if needed; but it is not compulsory. To be sure, I will stick to Lowe’s claim that metaphysical individuation is an explanatory relation of the non-causal variety, which has been widely accepted (e.g., Tugby 2017: 273). I will also assume, for the sake of the argument, that this relation possesses the right features to get Lowe’s argument started—a harmless enough assumption, given that most of them are standard features of explanation: qualms about such features, and thus about the viciousness of the above scenario, fall beyond the scope of this paper.⁶

So, let us call Direct Circularity the problem that the individuation of powers violates some of these features. Under these assumptions, Naïve DM surely suffers from a Direct Circularity. Lowe’s way out consists in the rejection of the claim that all properties are powers, thus a rejection of DM tout court; some properties do not require manifestations to be individuated, terminating the regress/circularity.

To be sure, the postulation of non-powers is not the only way out. The analogy with the individuation of sets may be helpful to articulate this point: according to Lowe (2010; 2012) given that the Axiom of Extensionality offers individuating conditions for sets in terms of their members, there is no need to postulate urelements, given that at the bottom of the hierarchy we can find a unique empty set, vacuously individuated through its lack of members.⁷ Thus, one may hold on DM by positing a null-power, viz., a unique power with no manifestation, safely sitting at the bottom of a (hypothetical) hierarchy of powers. This is unlikely to be a successful strategy, however, and not simply because it is usually assumed, as in Lowe (2010), that powers have at least one manifestation; the problem is rather that a null-power would be by definition excluded by any and all causal activity, thus making it an egregiously mysterious item which shouldn’t be postulated ad hoc to solve this difficulty. If one has to choose between non-powers and a null-power to escape the Direct Circularity, Lowe’s rejection of DM seems that much more appealing.⁸

3. Structuralist DM, and Its Problems

Bird’s (2007b) structuralist side-step can be intended as a solution to the Direct Circularity. In a symmetric structure at least two objects can be mapped one unto the other while preserving the overall structural pattern; roughly put, the structure does not distinguish between them. On the contrary, in an asymmetric structure each object occupies a unique position, which can be used to individuate it. Bird (2007b: 528) submits that, in the case of asymmetric structures, “the structure determines the identity of the vertices”, which might be taken to mean, in this context, that each power is individuated by the (asymmetric) power-structure it appears in; Bird never explicitly talks about positions, but this structuralist side-step has also been characterized by claiming that powers are individuated by the unique position they occupy in an asymmetric power-structure (e.g., Lowe 2010; Yates 2017).

Here is an important, albeit often-overlooked clarification. I will assume that Structuralist DM is dealing in concrete structures instead of abstract ones; here I am using “concrete” and “abstract” not in the sense usually meant by philosophers (to distinguish between what is spatiotemporally located, and what is not), but in a sense closer to a mathematician’s use of the words, and very similar to the distinction in Shapiro (1997) between “non-algebraic” and “algebraic”: a concrete structure, in this sense, consists in a system of objects and at least one relation imposed upon them; in a set-theoretical framework, this means that each concrete structure is a pair composed of a set and a set of n-tuples of members of that set. On the contrary, an abstract structure is an isomorphism-type of concrete structures; it is, loosely speaking, the structural pattern that any two isomorphic concrete structures have in common, and, as such, doesn’t exactly have objects as they do—if not in the somewhat ethereal sense in which its “places” are its objects. Individuating power-structures are structures of things, or objects (in the blanket use of “object” I am employing)—and more specifically, powers. So they are concrete structures. I suspect this assumption is implicit in much of the literature on DM (e.g., Bird 2007b).⁹

Structuralist DM, as claiming that powers are individuated by the structure in which they appear (or perhaps by a position in such a structure), may strike the reader as awfully circular: in fact, there’s at least three circularities at play here. Firstly, a Direct Circularity again. A structure of powers is most likely (partially) individuated by each of the powers that appear in it. Thus, given a power p₁ in structure S₁, it would be problematic to claim that p₁ is individuated by S₁, as S₁ is in turn individuated by p₁.¹⁰ Tugby has similarly claimed that

it is difficult to see how we can individuate the relevant power structure without at the same time individuating the powers that make up that structure. […A]mong those powers which help to individuate the structure in question will be the very power universal that we are trying to individuate in the first place. (2017: 274)

Again: two people taking each other’s washing. Tugby (2017) also suggests a more indirect circularity in Structuralist DM: an account of the individuation of powers must also provide individuation conditions of the power being individuated; a theory of individuation should not be circular in the sense that “the entity being individuated should not appear (either explicitly or implicitly) in its own individuation conditions” (Tugby 2017: 273). When that happens, we have what I will call an Indirect Circularity. Structuralist DM clearly incurs in an Indirect Circularity: a power is individuated as such-and-such on the condition that it occupies a specific position in a certain structure: but which one? Of course, the one it appears in.

A third circularity is highlighted in Yates (2017). This is merely the consequence of taking metaphysical individuation, as an explanatory/grounding relation, as imposing a fundamentality hierarchy amongst its relata (Tugby 2017: 4543). So, if p₁ is individuated by S₁, then S₁ is more fundamental than p₁. But this cannot be right, since S₁, as a structure with powers in it, and p₁ amongst them, would prima facie appear to be less fundamental than p₁ (perhaps, again under a set-theoretical understanding of S₁, under the assumption that sets are less fundamental than their members). Yates asks:

[w]hich came first, the powers or the structure? Assigning priority to the structure raises the obvious question of what it is supposed to be a structure of […]; on the other hand, to assign priority to the powers is to give up on the idea that they are relationally individuated. (2017: 4547)

(This perhaps resembles the “reality circularity” introduced in the beginning of the paper; but I won’t harp too much on this comparison). Let us call this difficulty, the Fundamentality Circularity.¹¹

Finally, there’s one more difficulty for Structuralist DM. Loosely put, the problem is that structures, or their positions, are too strange to be individuators for powers (as in Lowe 2010: 23). Positions especially are elusive objects, and it is far from clear how powers could be individuated by them.¹² This is of course no proper counterargument to Structuralist DM, as strangeness is no argument against anything; but it is a concern which adds to the aforementioned circularities to make Structuralist DM an even less palatable solution. Let us call it the Strangeness Concern.

In conclusion, Structuralist DM suffers from a Direct Circularity, an Indirect Circularity, and a Fundamentality Circularity. Furthermore, the Strangeness Concern looms over the position. What is particularly worrying, is that many of these problems appear to be variants of the same problems plaguing Naïve DM (roughly put, individuation circularities): no real progress appears to have been achieved through Bird’s structuralist side-step. I disagree, but to see this point, one must take a closer look at the notion of metaphysical individuation, which is what we now turn to.

4. Condition-First Approach to Individuation (and the Vindication of Naïve DM)

The reader may have noticed an oscillation concerning metaphysical individuation in the previous section. On the one hand, we have focused on metaphysical individuation as a binary relation between objects; on the other hand, we have claimed that individuation is about selecting conditions for the object being individuated: metaphysical individuation has close ties with the notion of transworld identity, in the sense that a principle of individuation for Ks ought to provide conditions for identifying Ks across worlds. So, on the one hand, a principle of individuation should provide individuators, viz., objects doing the individuating; on the other it should provide individuating conditions. Lowe himself shifts somewhat ambiguously between these two understandings, as he writes that

[i]ndividuation [is a] relation between entities: it is the relation of identity-dependence. A principle of individuation for entities of a certain kind K specifies what the individuators of Ks are. Such a principle provides a so-called trans world criterion of identity for Ks. (2012: 214–15)

Here the reader would assume that a principle of individuation should provide individuators for Ks in the sense of objects that individuate it; yet they are immediately corrected when Lowe claims that such a principle provides conditions for the individuation of Ks.

The best approach here would be, I suggest, to take metaphysical individuation as a binary relation between objects as, at best, a shortcut for a more complex notion. In this condition-first approach, a principle of individuation should provide conditions, more than objects.

There are two good reasons for the condition-first approach. First, an account of individuation cannot merely be exhausted by providing instances of binary relations between objects such as “x is individuated by y”, because such instances do not provide any transworld identity condition (they do not specify that y needs to be say, the manifestation of x, or that it is sameness of manifestation that sanctions being a specific power) and secondly, because such instances cannot be explanatory in any meaningful sense. About this second point, it is worth mentioning that objects do not explain—or, in other words, you cannot provide explanatorily satisfactory answers by merely citing or listing objects. Nor can an object be, on its own, something that requires explaining: something more structured is required (see Sider 2011: ch. 8). A binary relation between, say, fragility and breaking cannot be an explanation of anything: the former cannot be an explanans, and the latter cannot be an explanandum. On the other hand, that fragility is individuated, viz., that fragility is the very power it is, seems like a good explanandum; and some equally structured condition satisfied by fragility may provide a good explanans. Incidentally, this shift works exceptionally well to express the link between metaphysical individuation and transworld identity conditions: for example, Schbiden, in w₁, is individuated as Biden, in @, if and only if… (complete with your favorite transworld identity condition for persons).

If, as we have established, metaphysical individuation qua identity-dependence is an explanatory relation, one shouldn’t give much weight to the notion of a binary relation between objects: a different understanding of metaphysical individuation is required, which may lead to different understanding of the difficulties encountered by Naïve DM and Structuralist DM alike. This is worth stressing: if metaphysical individuation is not to be cashed out as a binary relation between entities, then the job of metaphysical individuation is not primarily to find “individuators”. Individuating conditions for a certain K might reference or quantify over certain items, and they might in a loose sense be called “individuators”, but this isn’t mandatory. As a matter of fact, there are many cases of individuals without individuators. A straightforward case would be the empty set. The empty set, like any other set, is an individual; viz., given a collection of sets, there is a fact of the matter as to which one of them can be individuated as the empty set (spoiler: the only one without members). Patently, here there are no objects being referenced or quantified upon in the right-hand side of the biconditional.¹³

Cases such as this are meant to show that there is no easy translation-schema between an object-first and a condition-first approach; it seems to me that, on the contrary, object-first locutions such as “…is individuated by…” always were a fallible shorthand for a more complex kind of relation. Sometimes, as in the case of the empty set, they break down entirely: the empty set does not have individuators, if not, perhaps a bit tortuously, its “lack of elements”; yet to take that at face value would be bad metaphysics.¹⁴

It is now time to express a bit more clearly our condition-first approach to metaphysical individuation. Let us employ some simple formal tool. “Ind(…,…)” is to be read as “…is individuated as…”; furthermore, for any x, if there is some y such that Ind(x,y), then we can say that x is individuated tout court, or that it is an individual. Given a collection of Ks, k₁, k₂,… and an arbitrary k, instances of Ind(…,…) provide answers to the question “which one of the Ks is k?”; if, say, Ind(k,k₂) then the right answer will be: “k₂”.

Let’s see if we can say a little bit more about this relation. That Ind(x,y) entails that x=y, but individuation is not exhausted by numerical identity: by the logic of identity, everything is identical to something, but not everything is an individual. There’s a special ingredient that separates individuality from self-identity. Usually the idea is that individuals have a privileged subset of essential properties that necessarily set them apart from others of the same kind, which are responsible for the object being metaphysically individuated (and thus an individual): such properties are responsible for any K being the very K it is, and not another: These properties are the ones specified by the relevant individuation conditions. For the purpose of this paper, we may take Ind(x,y) as a primitive.¹⁵

Now, what about metaphysical individuation itself? The crucial part within the economy of this paper is that, for two Ks x and y, if Ind(x,y), then this is because they both satisfy certain (kind-relative) conditions, which is what we properly call individuation conditions. That is to say: in metaphysical individuation, we settle what makes it the case, or explains, that a certain x is individuated as a certain y; what is being explained is thus an individuality fact, such as the fact that Ind(x,y). For example: why is it that a certain set s₁ is individuated as another set s₂? Because they have the same elements. Why is Schbiden in w₁ individuated as the actual Biden? Because… etc… You get the idea.

Following our previous take on individuation, let us consider a standard relation of (partial) non-causal explanation between facts (standard in the sense that it possesses the usual formal features of explanation, as above), expressed through “⟻”. Let us use the standard nominalizing device […] that turns closed sentences into names for facts; given sentences a and b, “[a] ⟻ [b]” is to be read as “the fact that a is explained by the fact that b”. Thus, metaphysical individuation is a subclass of non-causal explanations in which to be explained are individuality facts, for example, [Ind(k₁,k₂)].¹⁶

It will take some elbow grease to arrive at a satisfactory principle of individuation. The starting idea is, of course, that whether some x is individuated as some y depends on whether x satisfies a crucial condition satisfied by y as well. Thus, we might try the following (schematic) characterization of metaphysical individuation:

• 1)

  For any Ks x and y, such that Φ(y)

       [Ind(x,y)] ⟻ [Φ(x)],

where place-holder Φ stands for the individuating condition for Ks. For example, let Ks be sets, and Φ be “has as elements only and all the elephants”. Suppose that we have a set s₂ such that Φ(s₂); and we have another arbitrary set s₁ and we wonder whether s₁ is individuated as s₂; if it is, it is by virtue of the fact that s₁ also satisfies Φ.

The problem with (1) should be evident: ⟻, standardly, is factive. So (1) comes out as false on the simple assumption that at least for some x and y, x is not individuated as y. We need to recapture our previous intuition that whether x is individuated as y, depends on whether… etc… I will not expand my toolkit to make room for non-factive explanation or grounding, although I do not necessarily think there’s anything wrong with them. The simplest way to amend (1) is the following:

• 2)

  For any Ks, x and y, such that Φ(y)

       Φ(x) ⟶ Ind(x,y) & ([Ind(x,y)] ⟻ [Φ(x)]).

This unlovely mouthful reads: for any Ks x and y such that Φ(y), if Φ(x) then x is individuated as y, and the fact that x is individuated as y is explained by the fact that Φ(x).

A crucial thing to notice about any true instance of (2) is that, again, while x is being individuated as y, it is not technically individuated by any specific object, as opposed to another; the fact that x is individuated as y, on the other hand, is explained by another fact constructed with the help of the open formula Φ; this vindicates the condition-first approach to metaphysical individuation.¹⁷

Now, what about powers, viz., objects of kind P? According to DM, the individuation of powers is about sameness of manifestations. A power is individuated as, say, a power for breaking on the condition that its manifestation is breaking. However, because of multi-track powers, it wouldn’t do any good to simply define the Φ condition for the individuation of powers in term of a one-to-one predicate: for some x, y, and z, x may be a power to z, and y also may be a power to z—and yet we wouldn’t want to individuate x as y, because x and y might be distinct powers with partially overlapping manifestations. To solve this, I will deploy a resource not standardly used by power metaphysicians: plural logic. So, where “M(x,y)” is the binary predicate “x is a power to y”, or “y is manifestation of x”, “M(x,yy)” is defined as follows:

• 3)

  M(x,yy) =_df ∀y(y⥼yy ⟶ M(x,y)) & ∀z(M(x,z) ⟶ ∃y(y⥼yy & y=z)).

“x⥼xx” is the one-many predicate “x is one of the xx”. Now, according to M(x,yy), every y which is one of the yy is a manifestation of x, and any manifestation of x is one of the yy. In that case, we say that “x is a power to yy”—viz., the yy exhaust the range of manifestations of x. Single-track powers are a limiting case of multi-track powers, viz., powers whose manifestations are a plurality of one. We may define an individuating condition for powers Ψ as follows:

• 4)

  Ψ(x,yy)=_df M(x,yy)

Thus, we obtain a principle of individuation for powers:

• 5)

  For any powers P x, y, such that Ψ(y,zz)

       Ψ(x,zz) ⟶ Ind(x,y) & ([Ind(x,y)] ⟻ [Ψ(x,zz)]).

For clarity: zz should be read as a plural meta-linguistic place-holder. (5) is specific to powers, and thus is less schematic than the generic (2) given that the Φ place-holder for conditions has been substituted with the specific condition Ψ, but it is still to some extent schematic: just like sets, powers are all individuated in the same way, but each specific power is individuated through different facts, involving different manifestations. More to the point, (5) correctly rules that for some powers x, y such that y is a power to zz, if x also is a power to zz, then x is individuated as y—furthermore, it is exactly because x is a power to zz, that x is individuated as y. (5) is the simplest and safest way to implement individuation conditions for powers in terms of sameness of manifestations.

Here is a peculiar thing to notice: if pluralities can be empty (viz., ∃xx¬∃x(x⥼xx)), (5) allows for vacuous individuation, and can ensure the individuation and uniqueness of the null-power. One might protest: what are empty pluralities? And didn’t you argue against the null-power, anyway? Let me explain. First of all, I do not think that the null-power should be compromised by the logical form of individuation alone, as I argued against it on metaphysical grounds instead. Relatedly, the principle of individuation for powers has been taken to be analogous to that of sets throughout most of this debate; yet the analogue for sets of (5) does not allow for the individuation and uniqueness of the empty set, not without empty pluralities. According to Linnebo (2018), empty pluralities are a useful tool for formalizing set theory; now we can see that this is also true when it comes to the individuation of sets. Thus, I will keep (5), and its analogue for sets, which allows for vacuous individuation under the assumption that there are empty pluralities (still, I do not believe that there is a null-power).¹⁸

If (5) is intended as a principle of individuation for powers (according to Naïve DM), what is so problematic about it? The Direct Circularity seen before consisted in a violation of the formal features of individuation, as a binary relation between objects: but can we obtain a similar violation concerning instances of ⟻ in (5)?

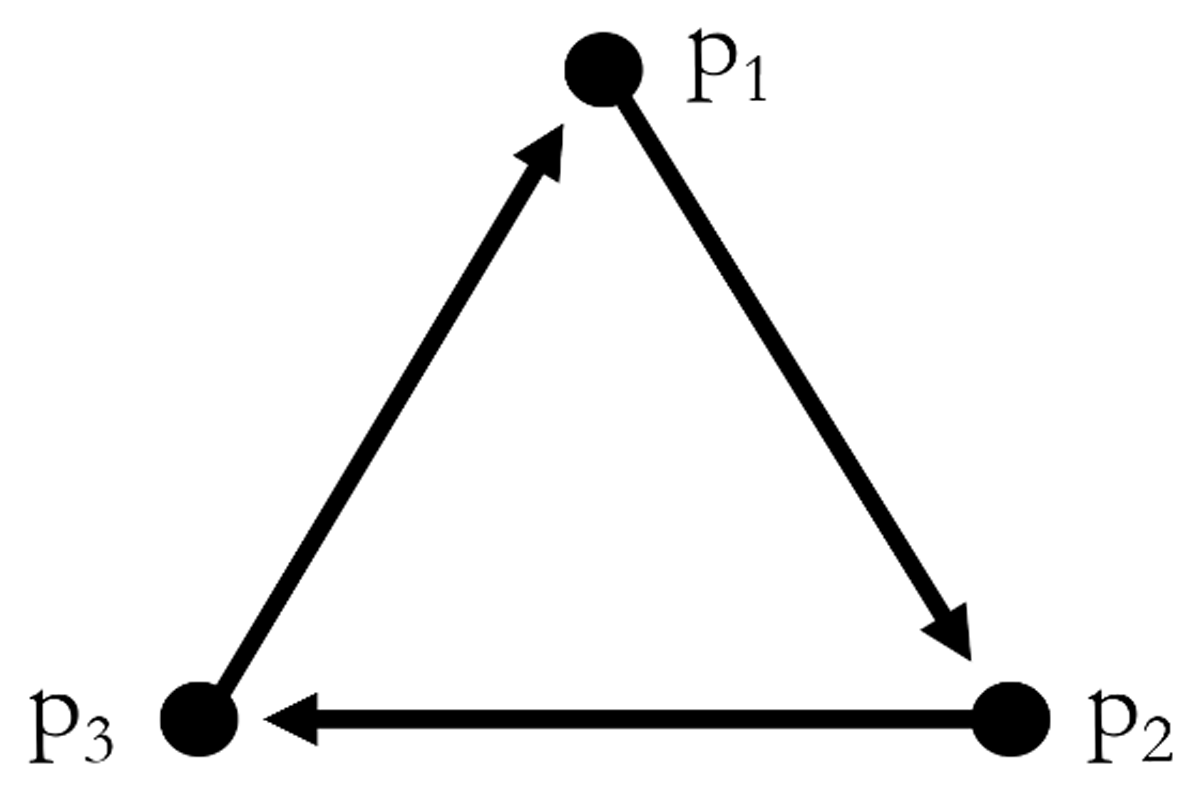
Let us consider a simple toy-world T, with a symmetric structure of powers as in Figure 1:

Figure 1

toy-world T

T is the perfect breeding ground for circularities: there are three powers: p₁, whose unique manifestation is p₂; p₂, whose unique manifestation is p₃, and p₃, whose unique manifestation is p₁. The received view is that individuating powers in T through their manifestations fails, and that therefore, if p₁, p₂, and p₃ are individuals at all, then they must have another source of individuality, such as a quiddity or something of that sort. But what is the problem here really, if there is one?

The metaphysical individuation of p₁, p₂, and p₃ in T amounts to the fact that, when given three arbitrary and similarly arranged powers q₁, q₂, and q₃ (whether in T, or some other world), it needs to be settled which power q₁ really is (whether p₁, p₂, or p₃), and similarly for the other two. Let us consider instances of ⟻, as obtained, in turn, by considering instances of (5), and let us call (for simplicity) pp₁ the plurality whose only member is p₁; and similarly for pp₂ and pp₃; thus, in our toy-world, M(p₁,pp₂), M(p₂,pp₃), and M(p₃,pp₁). Let us also begin by assuming, for the sake of the argument, that q₁ is individuated as p₁. Thus, by (5):

• 6)

  [Ind(q₁,p₁)] ⟻ [Ψ(q₁, pp₂)].¹⁹

That is to say: the fact that power q₁ is individuated as p₁ is explained by the fact that q₁ is a power to pp₂. Here’s two other true sentences in T:

• 7)

  [Ind(q₂,p₂)] ⟻ [Ψ(q₂,pp₃)]

• 8)

  [Ind(q₃,p₃)] ⟻ [Ψ(q₂,pp₁)]

However, and this is the crucial part, it is impossible to chain instances of ⟻ to obtain a Direct Circularity, simply because individuality facts do not appear in the right-hand side of it: the individuating condition Ψ(x,yy) does not require any power to be individuated in order to function properly. This is a good result for Naïve DM, as it shows that, once a sentence such as “p₁ is individuated by p₂” is to be understood as a roundabout way to express sentence (6), viz., “q₁ is individuated as p₁ by having pp₂ as manifestation”, we can see that the original Direct Circularity in metaphysical individuation, as expressed by Lowe, is dissolved.

An opponent of Naïve DM may reasonably feel an air of circularity here. Perhaps something along the lines of an Indirect Circularity is afoot, in which (according to Tugby) an object appears, either implicitly or explicitly, in its own individuating conditions. It is true that in any instance of ⟻, for example, (6), the power being individuated q₁ appears in the right-hand side of the formula. Yet I cannot possibly understand how this could be problematic. If power q₁ must be individuated, of course it—that very same power—must satisfy a certain condition Ψ: if this is not conceded, metaphysical individuation simply cannot get off the ground. Furthermore, this kind of “circularity”, if circularity at all, is unproblematic in the lights of the relation ⟻ that we are employing; for example, if [killing is wrong] ⟻ [killing is despised by God], then of course “killing” is mentioned in both sides of this claim—as some fact about killing is explained by some other fact about killing. And the same happens in (6): some fact about a power (that it is individuated as p₁) is explained by some other fact about it (that it is a power to pp₂). Tugby motivates Indirect Circularity as follows:

a principle of individuation must not be circular, which is to say that the entity being individuated should not appear (either explicitly or implicitly) in its own individuation conditions. The reason for this second condition is that the notion of metaphysical individuation is plausibly an explanatory one […] a principle of individuation, which picks out an entity’s individual essence, serves to explain why an entity is the very entity that it is. […] Given this explanatory role of individual essence, we can see why a principle of individuation ought not to be circular. (2017: 273)

I agree with Tugby that metaphysical individuation, as an explanatory relation, shouldn’t be circular, viz., the explanandum cannot appear in the explanans. But no such problematic circularity occurs whenever an object being individuated is present in the right-hand side of the individuation claim—because, again, merely listing or citing objects can neither offer nor require an explanation. In the condition-first approach put forward so far, the relata of metaphysical individuation, as an explanatory relation, are not the individuals themselves—they are facts (or perhaps true propositions, or something like that). Thus, an unacceptable circularity would be, for example, one in which Ind(q₁,p₁) is explained by Ind(q₂,p₂), in turn explained by Ind(q₃,p₃), in turn explained by Ind(q₁,p₁). But this is not how (5) functions. All in all, conditions of individuations for powers may very well refer to or quantify over powers, but, once we properly understand metaphysical individuation per the lines above, this is not enough to get to a circularity: we need to show that individuating facts are non-causally explained by other individuating facts.

How could we do that? The opponent of Naïve DM could retort: alright, but q₁ is individuated as p₁ by having pp₂ as manifestations, which dictates that the manifestations of q₁ need to be individuated as pp₂. Individuating powers still needs other powers being individuated. Alas, we’re back to a circularity.

I would answer: not quite. The key-word here is “need”. Of course if q₁ is individuated as p₁ by having pp₂ as manifestations, then their manifestations need—in the modal sense of “need”—to be individuated as pp₂. Individuating facts may very well modally co-vary with other individuating facts. But this needn’t necessarily translate into an instance of ⟻. In fact, there’s no reason why that should be the case. Think of it this way: that Fido is a good dog certainly requires that Fido is self-identical, or that it is individuated as such-and-such, but you wouldn’t include such things in the explanatory or grounding base of the fact that Fido is a good dog. Perhaps that Fido is a good dog is explained by the fact that Fido is loyal, or playful, or tranquil; of course Fido couldn’t be a good dog without being self-identical, or without being individuated as such-and-such: but one wouldn’t be very satisfied, in asking “why is Fido a good dog?” by hearing that Fido is self-identical, or individuated as such-and-such. It is reasonable to think of ⟻ as regulated by a relevance constraint, which prevents us to list just any necessary condition for p as a ground for [p]; according to Krämer and Roski (2015: 65), “the relevance constraint […] prevents us from enlarging the collection of facts that is to be the ground in arbitrary ways”. Necessary conditions need not be explanans, or grounds: relatedly, because ⟻ is not supposed to be a merely modal connection, we shouldn’t think of [Fido is self-identical] as explanans of [Fido is a good dog], just because Fido couldn’t be a good dog without being self-identical; otherwise [Fido is self-identical] would be the explanans of any and all facts about Fido. And the same goes for powers: q₁ couldn’t be individuated as p₁ if it weren’t the case that its manifestations were individuated as pp₂—but this is not what (6) states, nor can it be safely inferred from it.

In conclusion, if a condition-first approach to metaphysical individuation as a standard explanatory relation is on the right track, then (6)–(8) describes an unproblematic pattern of individuation of powers in terms of their manifestations. Thus, Naïve DM is safe.

5. Individuation as a sui generis Explanation (and the Vindication of Structuralist DM)

So far, we have proceeded under the assumption that our relation of metaphysical individuation is ⟻, a standard non-causal explanatory relation in which to be explained are individuality facts. But perhaps that was a mistake, and the last passage may offer a glimpse as to why.

5.2. ⟽ Vindicates Structuralist DM

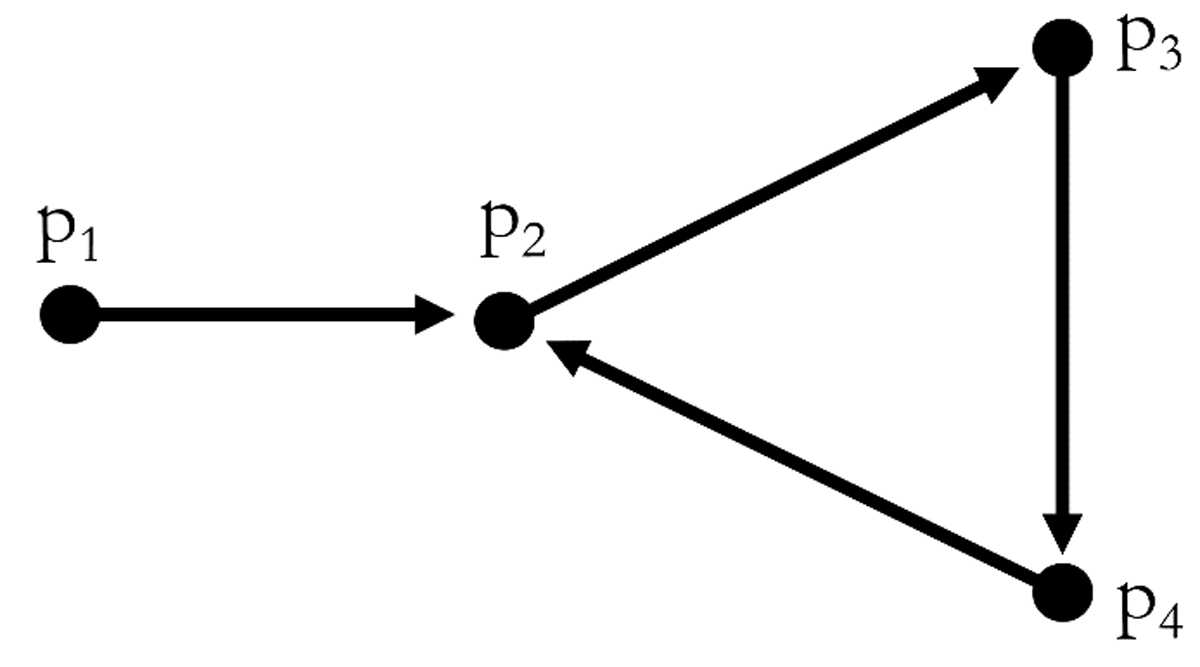
How to model Structuralist DM, within our condition-first approach to metaphysical individuation? We must abandon (5)^⟽ as a principle of individuation of powers in terms of their manifestation, and think of a condition involving the structure directly. Here is how we might proceed.²⁰ Consider Figure 2, which represents an asymmetric structure of powers (P₁), with four powers p₁, p₂, p₃, and p₄. (Note that, although P₁ has no non-trivial automorphism, it is still possible to formulate a Direct Circularity using (5)^⟽: in fact, there is a circular pattern of individuation between p₂, p₃, and p₄.)

Figure 2

structure of powers P1

I will begin with a complete description of P₁.

• 16)

  M(p₁,p₂) & M(p₂,p₃) & M(p₃,p₄) & M(p₄,p₂).

If we want to characterize the four powers merely through the structural information provided in (16), the simplest route is to “ramsify” it, to obtain the following:

• 17)

  ∃x₁∃x₂∃x₃∃x₄ (M(x₁,x₂) & M(x₂,x₃) & M(x₃,x₄) & M(x₄,x₂))

The easiest way to proceed, at this point, is to take (17) and unbind one variable at a time, to obtain every time an open formula that only one object in P₁ can satisfy. For example:

• 18)

  ∃x₁∃x₂∃x₃ (M(x,x₁) & M(x₁,x₂) & M(x₂,x₃) & M(x₃,x₁)),

where x is the free variable; let us call the open formula (18), Υ(x). Given the lack of non-trivial automorphisms in P₁, only p₁ can satisfy Υ(x): whether arbitrary power p in the structure can be individuated as p₁, is explained by the fact that p satisfies Υ(x). We might write something along those lines:

• 19)

  For any powers x and y, such that Ω(y),

         Ω(x) ⟶ (Ind(x,y) & [Ind(x,y)] ⟽ [Ω(x)].

(19) is schematic for place-holder Ω, which stands for unbindings of universally quantified complete descriptions of structures of powers. So understood, (19) reads as follows: for any powers x and y, such that y satisfies unbinding Ω, if x also satisfies it, then x is individuated as y, and the fact that x is individuated as y is explained (in the sui generis sense), by the fact that x satisfies unbinding Ω.

An instance of ⟽ is the one we have considered before, for example:

• 20)

  [Ind(p,p₁)] ⟽ [∃x₁∃x₂∃x₃ (M(p,x₁) & M(x₁,x₂) & M(x₂,x₃) & M(x₃,x₁))].

It is important to notice that (19) respects Bird’s original vision for Structuralist DM, exactly because it fails in the case of symmetric structures. Take a structure P₂ with a non-trivial automorphism in which two distinct powers p₅ and p₆ are mapped one unto the other. Thus, p₅ and p₆ satisfy the same unbindings; (19) would dictate that p₅ is individuated as p₆, and thus identical to it contra the initial assumption that they are distinct (the automorphism swapping them was non-trivial).

So far, so good. But how does (19) deal with the problems of Structuralist DM discussed in Section 3? Firstly, because individuality facts do not appear in the right-hand side of a ⟽ claim, no Direct Circularity can be straightforwardly formulated. Secondly, facts such as [∃x₁∃x₂∃x₃ (M(p,x₁) & M(x₁,x₂) & M(x₂,x₃) & M(x₃,x₁))] do not involve any reference to any specific power beyond the one being individuated, so the Special Rule of ⟽ does not kick in. Thirdly, the power being individuated does not appear in any open formula unbindings such as Υ, so no Indirect Circularity. Finally, because (19) does not reify structures, nor positions for that matter, it completely eludes the Fundamentality Circularity and the Strangeness Concern. Powers are not individuated by a structure or a position as an object: they are individuated by facts such as [∃x₁∃x₂∃x₃ (M(p,x₁) & M(x₁,x₂) & M(x₂,x₃) & M(x₃,x₁))], where no such objects are referenced nor quantified upon. More generally, moving away from a conception of metaphysical individuation primarily as a binary relation between objects—for the reasons submitted in the beginning of Section 4—also solves any problem that might arise from the ontological or metaphysical status of structures, or positions thereof. Retrospectively, it was somewhat awkward to conceive Bird’s structuralist side-step, in which powers are individuated as occupying a certain position in the structure, as an account in which powers are individuated by special position-objects. The awkwardness was caused, again, by the initial stipulation that metaphysical individuation is a relation between objects.

In conclusion, (19), as a schematic principle of metaphysical individuation, understood as a sui generis explanatory relation between facts, seems to have solved most if not all the problems laid out against Structuralist DM. Things start to look promising for its supporters, but there are still some issues to be discussed. There are two problems concerning (19)—none of which, at this point, is terribly new.

6. Concluding Remarks

It is finally time to take stock and draw some conclusions. A principle of individuation should provide both transworld identity conditions, and explanations concerning individuality facts; thus a condition-first approach to metaphysical individuation has been developed, different from Lowe’s standard understanding of individuation as a binary relation between objects. This radically changes the landscape of the individuation circularity arguments against DM.

There still is some uncertainty as to whether metaphysical individuation should be understood as a standard (⟻) or sui generis (⟽) non-causal explanatory relation, the latter being more apt at modeling failures of epistemic individuation; I did not decide one way or other, but if metaphysical individuation is to be modeled on epistemic individuation, then ⟽ is the way to go. Although I do not wish to settle this issue here, it bears noticing that Structuralist DM would appear to have the upper hand either way: if it can avoid the regress arguments formulated in terms of the more constrained ⟽ relation, then it can also avoid the regress arguments formulated in terms of the less constrained ⟻ relation.

Structuralist DM, so understood, constitutes a perfect example of how reasoning around metaphysical individuation is poorly served by Lowe’s notion of individuation as a binary relation between objects, viz., in this case supposedly obtaining between the power and a reified structure, or position thereof. Now, to be sure, Structuralist DM is not per se a flawless position; as many have noted (Lowe 2010: 21; Oderberg 2011), it is forced to the position that all actual and possible power-structures must be asymmetric, which may be problematic in a few ways, and may require sophisticated metaphysical tools to be resolved (e.g., again, the Platonism in Tugby 2017). Yet, once the asymmetry is conceded, the individuation of powers through power-structures is not by itself problematic.

In conclusion: if metaphysical individuation is understood through ⟻, then Naïve DM suffers no individuation circularity; if ⟽ is preferred, then it is Structuralist DM to walk away scot-free. The latter position is effectively free from all individuation regresses discussed throughout this paper, which may constitute a vindication of Bird’s structuralist side-step. All in all, the status of DM vis-à-vis individuation circularities is not as compromised as some have claimed—and Lowe’s intended way out (viz., to allow for non-power to eventually break the impasse) loses much of its initial appeal.