1. Introduction
Would you push the Fat Man off the bridge to prevent the trolley from killing five innocent people? You might vacillate between “I’d divert the trolley onto the one-person track; so, yes I’d give him the old heave-ho” and “no, pushing him is direct involvement in a way that’s different from pulling the lever.” Responding to thought experiments often involves reflecting on intuitions and principles in order to reach reflective equilibrium. We align principles we might commit ourselves to with cases we are willing to accept; we make sure the cases we reject do not fall under the principles.1 The principles are an attempt to “account for” the classification of cases being examined (Goodman 1983; Rawls 1971).
Once we sort out responses individually, we compare notes with what others think: Megan thinks it’s impermissible to push the Fat Man, but David thinks otherwise. Reaching equilibrium isn’t just about epistemic hermits aligning cases with principles. We’re interested in whether others share our assessments, in shared reflective equilibrium. That philosophers — or anyone trying to think carefully through cases and commitments—are interested in shared reflective equilibrium seems trivially true on reflection. Idiosyncratic intuitions don’t count for much in our social epistemic lives. It’s no coincidence that cultures all over the world devote time, money, and resources to collective interpretation of religious texts. And in many post-industrial nations, there are expensive schools devoted to teaching bright young minds how to argue for interpretations of laws—that this legal claim should be understood in that way.
These brief characterizations of reflective equilibrium highlight two kinds of questions. One is intrapersonal: for a particular person, will the method of reflective equilibrium yield a unique equilibrium? A moment’s reflection shows that this is no trivial question. There’s nothing in the method that promises a unique equilibrium is reached. From consideration of cases, individuals might oscillate among multiple equilibria; or they might be the ultimate fence-sitters, always saying “I can see that but…” Agents who successfully resolve conflicts between intuitions and principles are said to have reached intrapersonal convergence (i.e., reflective equilibrium at the individual level).
The other kind of question is interpersonal: would different individuals, each employing the method, converge on a unique reflective equilibrium? Again, there’s nothing in the method that would promise its users that different people would converge on the same reflective equilibrium, what we will call interpersonal convergence. Kelly and McGrath (2010) argue that intrapersonal convergence is necessary but insufficient for interpersonal convergence. For them, one reason there may not be a unique interpersonal equilibrium, despite everyone reaching intrapersonal equilibrium, is that different individuals might have different starting points.2
We agree with Kelly and McGrath that achieving intrapersonal equilibrium is necessary but insufficient for achieving interpersonal equilibrium, but we disagree with their explanation. We will argue that the method of reflective equilibrium itself allows for unique intrapersonal equilibria without a unique interpersonal one, even if individuals have the same starting point. The reason? The devil’s in the method’s details, particularly those details of just how agents bring principles and cases into alignment.
In this paper, we head into the underworld: providing a formalization of the method of reflective equilibrium that can be computationally implemented as an agent-based model. On the one hand, this forces articulation of hidden assumptions in informal descriptions of the method, and on the other, lets us use computer simulations to study emergent patterns from those assumptions. Our formalization allows us to identify scaffolding that must be in place in order to achieve shared reflective equilibrium. In a nutshell, we find that agents left to their own devices tend to diverge and that extensive support is needed to limit divergence. This support can come in various forms, such as shared intuitions about cases, starting with the same rules (principles), updating rules in the same way, using similar strategies for handling conflict between a principle and intuitions about a case, agreement on necessary conditions, etc. But even when such extensive support is in place, agents can still diverge. We argue from these results that to the extent that real communities of reflective agents manage to reach shared reflective equilibrium, it is unlikely that it emerges from the scaffolding we identify. Rather, reaching agreement is likely aided by additional forces facilitated by interactions between agents.
2. An Informal Model as Our Target System
Here is an example to get us started on thinking about the method of reflective equilibrium as the target system we want to model.3 Suppose you believe that average well-being should be maximized. You arrive at this by reflecting on other judgments you are willing to accept: people are better off when they have access to food and healthcare; folks prefer to be happy or satisfied as opposed to depressed. Principle in hand, you’re prepared to consider other cases. You get vaccinated because it results in greater overall well-being; you donate $100 to charity instead of buying a bunch of lottery tickets. These are cases in which the action you are inclined to choose is determined by your principle.
Suppose, however, someone were to argue that eugenics can maximize well-being (Veit, Anomaly, Agar, Singer, Fleischman, & Minerva 2021). And suppose further that you find this intuitively false. You recognize there’s evidence on the one hand that you should accept that eugenics is permissible (given your principle) but you intuit the conclusion is wrong. What should you do? It seems like there are four options:
Ignore the intuition: Sticking with principles is sometimes the epistemically responsible thing to do, so you might have a mantra to remind yourself not to get hung up on the intuition.4
Postpone consideration of the case: Set the case aside for now and come back to it later; maybe you look at other cases in the meantime.
Change the principle: Perhaps maximizing average well-being is too simple to accommodate intuitions about right and wrong.
Change the tolerance for principle satisfaction: Perhaps you identify ways that the test case is dissimilar from the cases described by the principle.
In short, given some tension between a principle (or set of principles) and an intuition about a case, we can ignore intuitions, put off the decision to a later date, change the principle, or change how tolerant we are of cases deviating from our principle. This is how the process seems to go when agents have a kind of localized access to the universe of possible cases, when they deliberate one case at a time. Consider areas of inquiry that utilize thought experiments, like Gettier cases and the resulting cottage industry of developing new accounts of knowledge and counterexamples. Trolleyology is another. So in our target system, we are imagining that agents are simultaneously exploring the space of cases while engaging in the reflective process, much like how philosophers seem to do.5
It’s worth a bit of space to explain how this conceptualization of the target is similar to—but also importantly different from—other ways one could describe the target system. We begin with differences. Canonical descriptions of reflective equilibrium leave open how the reflective process unfolds. For example, Goodman (1983: 64) described the process of making “mutual adjustments between rules and accepted inferences” in order to bring into agreement rules and particular inferences.6 That kind of description leaves open to refinement whether an agent already has all the cases to be considered at hand (but commitments to the cases might need revising), or whether the relevant adjustments are to be made dynamically as new cases are coming in. Our informal description is an instance of the latter. Beisbart, Betz, and Brun (2021) (which we’ll refer to as the ‘BBB’ model) is an excellent example of formally investigating the former conception of the target system (where all the cases are in, but commitments can be revised). Let us give a brief a description of the BBB approach to then highlight some key differences to help clarify what we have in mind for our target system.
In the BBB model, agents have global access to the pool of sentences with inferential relations between them. At the beginning of the reflective process, agents have initial commitments over some of these sentences. A theory T is a set of sentences also from the sentence pool. Progress of a theory T towards equilibrium is measured by degree of satisfaction of three desiderata: account, systematicity, and faithfulness. Account is a function of the number of commitments inconsistent with T, the number of commitments not entailed by T, and the number of commitments entailed by T that the agent is not committed to. Systematicity is a function of the number of principles constituting T and the number of sentences in T. Faithfulness is a function of how far commitments at time t+n have moved away from the agent’s initial commitments at time t. Notice that all three of these desiderata come in degrees, which plays a crucial role in the process of equilibration; influence of these desiderata on progress towards equilibrium is modulated by weighting coefficients summing to one. Starting with some initial commitments C0, agents search for a theory T′ that scores best on the measure of account and systematicity (according to some specified weighting of the two). Once an agent has identified such a theory, they then turn their focus on their set of commitments, searching for a set of commitments C′ that scores best on some weighted balance of the measure of account and faithfulness. This back and forth process is iterated until no further changes in theory and set of commitments occur. What is interesting about this way of conceptualizing the reflective process is a better understanding of how different desiderata—account, systematicity of theory, and faithfulness—can be traded off against each other when assessing reflective equilibrium processes that amend theories and accept/reject commitments.
As we see it, there are three key differences between our conceptualization of the target system and BBB’s. First, while the BBB version has a fixed set of cases (sentences) that agents have global access to, in our version agents are more cognitively bounded with “localized” access to the universe of cases. Again, we wish to capture the idea that new cases, illustrated perhaps by thought experiments, can be thought up or discovered. The second difference is related: the process has both intrapersonal and interpersonal elements, with agents having differentially shared characteristics and the ability to interact with each other (we will unfortunately not have the space to explore interactions in much detail in this paper, but we will discuss this briefly in the conclusion). Some of these differentially shared characteristics might be captured on the BBB account with different weights on the measures of account, systematicity, and faithfulness. But such comparisons will, at best, be partial since our target is explicitly a piecemeal process. For example, there is no “postpone consideration” option in the BBB model because cases are given all at once.7
The third key difference concerns the role of intuitions. We agree with Brun (2014) that intuitions are non-inferential and that the method of reflective equilibrium does not essentially involve intuitions. Consequently, intuitions do not appear in the BBB version. But as Brun also points out, the method does not preclude intuitions either. At least in epistemology, for better or worse, intuitions have historically played a role in the process of updating theories of knowledge (and arguably they play a similar role in trolleyology). We want to capture some aspects of the functional role that intuitions can play in the reflective equilibrium process. Admittedly, this means we might be capturing only some fragment of some larger target system of reflective equilibrium. It might be that our model is nearer to what might be described as the narrow version, where it is possible that justification does not emerge from agreement between principle and cases.
There is one more point of comparison worth bringing up. Goodman’s characterization of the process leaves open whether agents begin with a rule and refine it in light of cases or generate a rule based on a few cases and then refine it through consideration of further cases as well as considerations that are arguably considered to be a part of a “wider” reflective equilibrium (e.g., background theories, and perhaps theoretical virtues as well).8 Our conceptualization of the process imagines agents “beginning” with a rule, refining it against cases throughout the simulation.9 We understand the process in this way for several reasons. First, when engaging in reflective equilibrium, agents aren’t blank slates. We come to the process with previous experience as well as biases and heuristics we use in thinking through cases. We capture this in having our agents begin with rules rather than developing them through consideration of cases. Our agents stick closer to Bayesian notions about updating. Bayes’s rule is effectively an instruction about how to update hypotheses in light of new evidence. The updating procedure refines the hypothesized rule, but is silent on where it comes from.10 Second, given our agreement with Brun (2014) about the role of intuitions, we are agnostic about the processes by which agents generate initial hypotheses. Our agnosticism on this front is built into the model by assigning initial rules (more below in the description of our model).
Generally, we do not think there is sufficient agreement in the literature to say that there is the target system of reflective equilibrium, nor that there is a precise distinction between narrow and wide versions of it. What our brief comparison to the BBB model is intended to show is that before we even get to a formal model, there are different ways in which we can informally conceive of the target system, each satisfying the characterization in Goodman (1983). To be sure, there is significant overlap in these informal descriptions, and there are some aspects of our model and the BBB version (and others that are likely to come) that we can translate between. But just because a pickup truck and a sedan are both vehicles doesn’t mean we get to make direct evaluative comparisons between them: each serves different (with some overlapping) purposes. Our model, for example, might be construed as a limiting case of the BBB version when the measure of account is required to be maximal throughout the equilibriation process. But given significant differences elsewhere in the model, not to mention the above differences in our target systems and our focus on the interpersonal question, we think readers should resist the exercise of making direct evaluative comparisons.
Let us return to the description of our target system. While it is a start, this informal model lacks sufficient detail to tell us what the answer is to the intrapersonal question: whether a person is guaranteed to arrive at a unique equilibrium. An important point glossed over is the existence of choice points at which agents have to decide how they’re going to reconcile the tension.11 In token applications of the reflective process, agents will have to choose which of the four options listed above they’ll use to ease the tension; these are the choice points. For all we know, taking different options at choice points can lead to different intrapersonal equilibria.
For example, suppose Tweedledum and Tweedledee begin the reflective process from the same starting point and have been considering the same cases up to time t without any intrapersonal tensions between intuitions and principles. Suppose at t a case is considered that reveals a tension between an intuition and a principle. Since we are considering the intrapersonal question, we’ll suppose that there is no explicit coordination between our two characters. Then as far as the method has been described, it is possible that Tweedledee opts to ignore their intuition while Tweedledum changes their principle—both correctly apply the method. Assuming that the reflective process converges at all, we can ask: will this difference in choice for handling the tension ultimately wash out by the end of the reflective process, leading Tweedledum and Tweedledee to the same equilibrium? Or can such a choice point change the trajectories of Tweedledum and Tweedledee’s reflection such that they land at different equilibria? Moreover, if Tweedledum and Tweedledee do land at the same equilibrium, is this a matter of necessity given the intrapersonal application of the method, or is the uniqueness contingent on the particular history of implementing the reflective process? Put differently, it might be that agents’ histories of choices foreclose attaining particular equilibria. Thus convergence towards the same equilibrium may reflect sufficiently similar histories of choice points in the application of the method, as opposed to something about the domain in which Tweedledum and Tweedledee are deliberating. This could be even if (from a God’s eye view) they pre-reflectively have the same intuitions, and even if those intuitions are about some necessary conditions (we give this possibility its own treatment below in Section 4.3).
Similar kinds of considerations can be given to the interpersonal question. Suppose that throughout the reflective process Tweedledum and Tweedledee occasionally meet to discuss their progress. Assuming that by the end they land at a shared reflective equilibrium, we can ask: how much of the interpersonal convergence can be accounted for by the process (including overlap in their intuitions) that lead to intrapersonal convergence? How much did their interactions with one another aid in getting to shared reflective equilibrium? Answers to these questions can have important impacts to the broader literature on reflective equilibrium, which we address later.
It is at this point that further refinement of our informal model is significantly aided by a more formal version. When constructing a formal model we are faced with numerous decisions. Modeling, by necessity, involves idealization and abstraction.12 There is a delicate balance in these choices. On the one hand, if the model is an over-simplification of the target system, then the patterns of the model’s behavior will not be inferable to the target. On the other hand, if the model is an under-simplification, it runs the risk of being intractably complex and inhibits our ability to suss out patterns in model behavior. One strategy for handling these demands is to make modeling choices in such a way that when we de-idealize from the model to the target system, the patterns will change in a predictable way.13
We follow this strategy to avoid the twin dangers of under- and over-simplifying the model. When representing the process of achieving shared reflective equilibrium, our modeling choices favor the success of the method, particularly in the intrapersonal process. Adding complications that were left out in the model should make it more difficult to reach an equilibrium, not less (given our target system). Consequently, patterns in the model’s behavior that depend on agents having reached intrapersonal equilibria should be preservable in inferences we make to the method as it is captured by the target system. So while it will be true that our model is false (as all models are) the lessons that we learn will be preserved when we de-idealize and consider how the actual method works as far as the informal characterization goes. If something cannot be achieved in the best-case scenario that our model favors, we should not expect it to be achievable in less ideal situations; real agents won’t converge on equilibria more effectively than our idealized ones.14
As we’ve mentioned, our interest is in understanding shared reflective equilibrium, which involves agents independently arriving at a reflective equilibrium and then comparing their results. Given the focus on agents, our representation is readily amenable to the agent-based modeling framework. In this framework, individuals and their interactions are explicitly represented in a computer simulation. For the particular questions we are interested in, agents do not influence one another. Our primary interest is in formalizing the process of reflection, understanding how that process leads to intrapersonal convergence, and under what conditions we can expect those reflective equilibria to be shared when agents work in their own arm chairs.
3. Modeling (Shared) Reflective Equilibrium
We describe our formal model in four parts. First, we explain how we opt to represent cases and principles (or “rules”). Second, we give definitions of reflective equilibrium and the functional role of intuitions. Third, we describe the dynamics of the reflective process, paying particular attention to different ways that conflicts between intuitions and rules could be resolved. Fourth and finally, we describe our simulations, noting specifically different ways the process can be initialized and the sorts of things that agents can have in common, including the possibility that their intuitions are systematized (pre-reflection) around necessary conditions.
3.1. Cases and Principles
The task of an agent is to bring a principle and a set of cases “into alignment”. We formalize the idea of a case as a string of yes/no responses to questions that determine the features of a case. For example, we can imagine a set of Gettier-style cases that each differ on some condition, like different versions of the same story in which subjects are asked to classify whether “Emma knows she has a diamond in her pocket”.15 Some versions of the story will have a “failed threat” in which, for instance, a thief tries to steal the diamond but fails. In other versions the thief succeeds, but someone else slips a diamond into her pocket shortly after. Still in other versions the original object was a fake, only to be replaced by a real diamond later. And on and on they go. Each version of the story has some set of features and not others. We encode each feature as an index in a string of yes/no. So YYYN16 would represent one kind of case while YYNY another. In addition, we will consider a variation on this representation where cases have hierarchical structure, so that features are not merely independent characteristics that make up cases. For example, YYYN and YYYY can be more similar than YYNY and YYYY if features to the left take precedent over features to the right.
Representing cases as strings of bits has several useful features. We can have a measure of distance between cases by using the Hamming distance, the number of positions at which the corresponding strings are different. For example, YYYN and YYNY have a distance of 2 because they differ in two positions. This in turn is useful in thinking about sets of cases that have the same length. For example, we can ask whether the cases in one set are more similar to one another than the cases in another set. Suppose we have two sets of cases, A={YYYN, YYNY, YYYY} and B={YYYN, YYNY, NNNN}. We can say that the cases in A are more similar to each other than in B by doing a pairwise comparison of the cases in a given set and noting the largest Hamming distance, that is, the greatest number of mismatches between strings in a set. In the case of A, this would be 2, where in B it is 3.
Because the maximum Hamming distance h will be relative to the length of the strings being compared, we adopt the following convention in which we normalize distance between cases (of the same length). The similarity score for a set of cases is calculated as follows. Let hnm be the normalized Hamming distance for each pair of cases n and m in a set. The similarity score for a set S is
(1)
So when two cases disagree at all their indices, for example, the normalized Hamming distance is 1 and the similarity score for the set to which they belong is is 0. The similarity score increases as the maximum Hamming distance for pairs in a set decreases, with the highest similarity score being 1, which only singleton sets can have.
There are three classifications of cases relevant to the method of reflective equilibrium: i) ACCEPT, which comprises all the cases an agent assents to, ii) REJECT, all the cases that an agent dissents to, and iii) UNCLASSIFIED, all the cases that an agent has not yet classified. Unclassified cases are of two kinds: cases that have yet to be considered and cases that are postponed for later consideration (more on postponed cases later). All cases belong to one of these three sets: the ACCEPT set, the REJECT set, and the UNCLASSIFIED set. We discuss ACCEPT and REJECT lists in greater detail in Section 3.2.
We represent a principle (or “rule”) as a pair, with the first member being a “center” case, and the second member being a tolerance score threshold. This threshold sets the maximum normalized Hamming distance17 that cases are allowed to differ from the center case. Together, these determine the extension of the principle. For example, suppose the case is YYYY and the threshold is 0.25, then the extension of the rule is: <YYYY, 0.25> = {YYYY, YYYN, YYNY, YNYY, NYYY}. We say that principles are more permissible or tolerant as the threshold increases.
Note that at a threshold of 0.5, the extension of a principle will include cases that are pairwise inconsistent. For example, if the center case is YYYY, then even though NNYY and YYNN are within a 0.5 threshold of YYYY, they have a similarity score of 0. In addition, take care not to interpret pairwise inconsistency as a contradiction, that is, NNYY and YYNN are not contradictory.18
One final point about cases and principles:19 once an agent reaches equilibrium, cases and principles are biconditionally related.20 But this simplification fails to capture that rules might be equivalent but expressed differently or that sets of rules are brought into alignment with cases. We adopt this approach again with a bias towards agents reaching intrapersonal equilibrium: balancing a single rule with a set of cases is a simpler task than balancing a set of rules. We hope to explore some of these variations in future work.
3.2 Reflective Equilibrium and Intuitions
To be in reflective equilibrium there are three conditions to be satisfied: i) every member of ACCEPT falls under the extension of the principle, ii) every member of REJECT falls under the complement of the principle’s extension, and iii) UNCLASSIFIED is empty. We say a pseudo- reflective equilibrium is obtained when conditions (i) and (ii) are satisfied, but cases remain in UNCLASSIFIED.
Our definition of reflective equilibrium above lets us determine the number of possible equilibria there are for strings of length n. Two of them are trivial. The first is when all cases are in ACCEPT (and REJECT is empty) and the second is when all cases are in REJECT (and ACCEPT is empty).21
The other possible equilibria can be counted by noting two features. First, the extension of a principle has a unique center case. Second, given a center case, each non-trivial threshold level defines a unique extension.22 So to calculate the number of possible equilibria, we need only count the number of possible (non-trivial) principles. For strings of length n, there are 2n possible cases, any of which can be the center of the principle. And for each of these center cases, there are n – 1 non-trivial thresholds that define various levels of tolerance in principles.23 Hence the number of non-trivial principles (and therefore equilibria) is (n – 1) * 2n.
Knowing the number of possible equilibria is important for assessing the probability that two agents reached the same equilibrium by chance. If we only consider cases of length 2, then there are 8 possible equilibria. If we assume that each non-trivial equilibrium is equally likely to be reached, then there is a 4/16 = .25 chance that two agents share an equilibrium. This probability decreases substantially as the cases become more rich (i.e., as n increases). For example, for n = 5 there are 32 possible center cases, 128 possible equilibria, and a chance of 128/16,384 = 0.00781 that two agents happen upon the same equilibrium.
When we’re thinking about reflective equilibria in practice, it is unlikely that each possible equilibrium is equally likely to be reached. Philosophers and lay-people alike have intuitions about what seems right. For many Anglo-American philosophers, it’s intuitive that Smith knows the person with ten coins is getting the job or that Singer’s passer-by should ruin their shoes to save the drowning child. We allow for intuitions to play similar roles in our model by allowing cases to come with intuitions. A case might come with an intuition that it should be classified in ACCEPT, or in REJECT, or it might not come with an intuition at all. Moreover, we acknowledge that intuitions about cases can change over time. We thus encode intuitions as labels on cases, which can, within reason, be removed or added. Explicitly, we use “NI” when there is no intuition for a case, “IA” when a case should be intuitively accepted, and “IR” when a case should be intuitively rejected.
Intuitions are important drivers in the dynamics of the model, particularly in the reflective process. We strive to functionally represent them in the way that they are conceived of as ‘considered judgments’ in the technical sense: they are issued when one is able to concentrate without distraction about the topic at hand and are stable over time, but it is reasonable to select some intuitions and exclude others (Rawls 1971: 47). Intuitions proper are arguably not the same as considered judgments (see Brun 2014) and some care needs to be taken in interpreting them beyond the functional role we have given them here. We will describe below how we can use them on aggregate to “cluster around” a particular feature, simulating the idea of necessary conditions.
3.3. Modeling the Reflective Process
Our representation of the reflective process is drawn from the idea that principles are arrived at by means of reflection on cases, as in Goodman (1983). On our representation of principles, the center case functions as a paradigm and the tolerance threshold determines how far from the paradigm the agent is willing to go. There are many ways to be out of reflective equilibrium. Our aim is to characterize the method in a sufficiently general way so that an agent is able to bring a principle and cases into alignment regardless of their starting point. Given our representation of principles, this will involve making adjustments to the center case and the tolerance threshold.
From a high vantage point, an agent goes through the following steps:
Get a case from UNCLASSIFIED
-
Test case against rule
-
If case is labeled “NI”:
If case is within tolerance of rule: put case in ACCEPT
Else: put case in REJECT
-
If case is labeled “IA” or “IR”:
If case is IA and within tolerance of rule: put case in ACCEPT
If case is IR and outside tolerance of rule: put case in REJECT
Else, Deliberate
-
For most of the steps above, there’s not much to see—an agent is simply sorting cases. However, in step 2.b.iii agents find themselves in a situation where their intuition differs from how the rule says the case should be classified. Consequently, the agent makes a call to a procedure called Deliberate.
Deliberate is intended to approximate what really happens. When our intuitions about how to classify a case differ from how the principle would classify a case, the following options are available: i) we can suppress the intuition and classify however the rule tells us to, ii) we can change the principle, or iii) we can postpone consideration of the case and come back to it later. With respect to changing the principle, there are two subsequent possibilities: we can change the tolerance threshold (become more or less permissive), or we can change the center case.
We can imagine that agents might differ in their dispositions with respect to strategies. Some agents might have a preference for “sticking with their principles” and devaluing their intuitions, others “go with their considered judgments” and are more likely to change their minds about principles, while still others tolerate cognitive dissonance and put off the resolution of the conflict until some other time. We are interested in understanding whether and how different strategies impact shared reflective equilibria.
We define four types of agents whose dispositions can very in strength:
Rule-changer: Disposed to change the center case in such a way that the new rule classifies the incoming case according to the intuition the case is labeled with.
Tolerance-changer: Disposed to change the tolerance threshold in such a way that the incoming case is classified according to the intuition of the case.
Peeler: Disposed to “suppress” the intuition by removing the intuition label on the case and then classifying it according to the rule.
Postponer: Disposed to put the current incoming case in a temporary postpone list and classify other incoming cases in the mean time. The case is “flagged” and ultimately the intuition label is stripped, avoiding situations with incompatible intuitions (more below).
All of these strategies can be used at different levels in mixed strategies, with one being more dominant than the others. For example, when an agent has a 94% disposition of being a Rule-changer, they will use the other three strategies 2% of the time each. We also have Randos—agents that pick one of these strategies at random.
Both tolerance-changers and rule-changers make adjustments that could affect the stock of cases that they’ve already accepted or rejected. If one of these agents changes their center case or tolerance threshold, then cases that were previously accepted might no longer be in the extension of the principle.24 We follow a conservative strategy: any proposed changes to the center case or the tolerance threshold cannot end up removing a case from ACCEPT or adding a case to REJECT. That’s to say, changes to the principle are constrained by the agents’ previous judgments. In this same spirit, when tolerance-changers adjust their thresholds, they modify it just enough to accept IA cases (or reject IR cases), while constrained by the commitment not to re-adjudicate cases.25
So in effect, to accept a case is to assent to the case as an instance of the rule; all accepted cases are in the extension of the rule. To reject a case is to dissent to the case as a rule-instance; all rejected cases are not in the rule’s extension. This is another idealization: given a rule, agents never misclassify a case. If a case is in an accept list, it’s because it is in the rule’s extension. (Mutatis mutandis for reject lists.) Rules and ACCEPT (and REJECT) are in perfect alignment. For our idealized agents, once a case is accepted or rejected it stays there. It constrains future rule updates.
While this seems like a strong requirement, it is an example where we choose a simplification that favors reaching reflective equilibrium. We could have added procedures that handle re-adjudication, but that would require bringing on additional assumptions and the possibility that reaching reflective equilibrium is not guaranteed. That said, we don’t object to the addition of such procedures, they are rather complications that would distract us from our aims here.
The Rule-changer has further choices to make; namely, how radically are they to revise their center cases? We think it reasonable that principles change conservatively, that is, that there is a good deal of overlap in the extensions of the new and old principles. To this end, rule-changers figure out the minimum number of changes they have to make to their current center case to classify the incoming case with its intuition accordingly—provided, as just mentioned, no re-assignments of already-judged cases are required. Still, there are options. For example, suppose an agent has the rule <YYYN, 0.25> and is considering the case IA-NYYY.26 The Rule-changer has a choice between <NYYN, 0.25> and <YYYY, 0.25>. How does it decide which to adopt?
In our model, we consider two possibilities. The first is that a Rule-changer picks one of the available options at random. The second is to interpret strings hierarchically, so that we privilege some indices over others, say earlier ones over later ones (left to right). In effect, this would be like placing more importance on some features of cases over others. This second option will turn out to be important in our analysis because it is one way in which agents might “coordinate” in their changes without exerting direct influence on one another.
A brief note about the Postponer strategy. Recall that we want to design things in such a way that reflective equilibrium should be readily achievable, specifically, we want to ensure intrapersonal convergence. We thus ensure that reflective equilibrium can be achieved by agents having to consider any given case at most twice—by the second time the case is stripped of its intuitive label. This avoids infinite loops agents might otherwise find themselves in by re-classifying cases again and again in an attempt to reach a reflective equilibrium that is not attainable, for example, when a set of intuitive cases are impossible to classify under any rule.27 Skeptics of the reflective equilibrium method might be interested in how this choice point, along with others, could be used in arguments that reflective equilibria are in fact not achievable. But that is not our goal here. For our purposes, the reflective process is guaranteed to terminate in intrapersonal reflective equilibrium.
3.4 Initialization and What Is Shared
On an individual basis, the reflective process in our model ensures that, given any rule that an agent might start with, the agent will attain intrapersonal convergence. Our primary question now is about interpersonal convergence: will two or more agents reach shared reflective equilibrium? That is, will agents engaging in their own reflective processes terminate with the same rule and ACCEPT and REJECT lists? Whether agents reach shared reflective equilibrium will turn out to depend on how many other things they share. Here are the possibilities of what else agents can share in our model, which we can set as part of how simulations are initialized:
Shared starting rule: All agents start with the same rule, including both the center case and the tolerance threshold.
Shared deliberative dispositions: All agents are disposed to use the same deliberative strategy equally as often.
Shared privileging of features (Or: “Coordinated” rule change): All agents agree on a hierarchy of features of cases that are more important than others and make rule changes on less important features first, though each agent decides on their own change.
Shared ordering of cases: All agents consider the cases in UNCLASSIFIED in the same order, that is, they do not individually “shuffle” the cases before doing the reflective process.
Shared volume of intuitions: All agents have the same proportion of intuitive cases to all cases. That is, no agent has more intuitions than any other agents.
Shared intuitions: All the cases to be classified have the same intuition labels across all agents.
Pre-reflection systematized intuitions: Intuition labels can be assigned to cases randomly before cases are considered, or in a systematic fashion so that they “cluster” around, for example, necessary conditions.
As the results below will show, whether agents are able to reach shared reflective equilibrium (SRE) will depend on carefully calibrated conditions. In short, in order for agents to reach SRE, we have to heavily stack the deck by ensuring that agents have a sufficient number of the above shared items. And even then, we only see SRE among all agents in very limited scenarios. Unfortunately, most of these situations are implausible in actual practice.
4. Results
We discuss the results in three parts. First, we look at how much “coherence” is introduced by the deliberate procedure. Many places in the literature identify reflective equilibrium as a coherentist method, as opposed to (say) foundationalist (see Daniels 2020 for an overview). That is, while some intuitions or judgments about cases can be stronger than others, there is no bedrock that is absolutely non-negotiable.28 Similarly, there are no foundational intuitions for our agents—it is possible, at least in principle, that for any given case with an intuition label, the agent can disregard the intuition. Moreover, it is possible for us to assign intuitions to cases in a systematic or non-systematic way (see Section 3.4). Effectively, this allows us to explore the possibility that intuitions are not guaranteed to be coherent; assigning intuitions non-systematically enables the possibility of pairwise-inconsistent cases being tagged “intuitive accept.” Since coherence isn’t presupposed in that initialization, any coherence that emerges must be a result of the strategies that the agents deploy, that is, the method of reflective equilibrium.
Second, we look at how the number of shared reflective equilibria (SRE) depends on various strategies and parameter values when intuitions are initialized non-systematically. We particularly explore ranges of parameter values that reduce the number of equilibria and help our small community of agents achieve SRE. While it is possible for our community of agents to achieve SRE, we have to make implausible assumptions about method implementation for them to pull it off.
Third and finally, we look at what happens when intuitions are initialized to be coherent and even systematically clustered. Here the thought is that intuitions might cluster around some cases, so as to simulate a necessary condition, and that such clustering might drive individuals towards one set of principles as opposed to another. If that were the case, and assuming that all agents have the same “a priori” intuitions, then we find that SRE is indeed more likely. However, again, it is still not guaranteed and the plausibility of the surrounding assumptions remains questionable.
Table 1 shows a summary of the parameters and their values we explored. For the results we present, we have ten agents in our community, so the number of possible equilibria can range from 1 (completely shared reflective equilibrium) to 10 (no reflective equilibria are shared). We used Netlogo 6.2, a programming language and integrated development environment, to implement our model, available at http://modelingcommons.org/browse/one_model/6812. Our analysis of simulations is performed in R version 4.0.2. Both data and script for analysis are provided as additional files at the link provided. Plots not shown here can be seen by running the R script on the supplied data set.
Summary of parameters and values for model simulations.
| Parameter | Values |
| Disposition | 90, 92, 94, 96, 98, 100 |
| Tolerance | 0.2, 0.4, 0.6, 0.8 |
| Agent type | rule-changers, tolerance-changers, randos |
| Intuitive cases as a proportion of all cases | 0.02, 0.04, 0.08, 0.10, 0.20, 0.30, 0.40, 0.50, 1.00 |
| Coordinate on center case changes | True, False |
| Shuffle center cases | True, False |
| Shuffle agent case order | True, False |
| Cases have necessary condition | True, False |
4.1. Coherence
Reflective equilibrium is typically understood as a coherentist epistemology. Here, we provide a sanity check on the model: agents with tolerance levels greater than 0.5 should have less coherent ACCEPT lists relative to agents with levels less that 0.5 (recall: two pairwise inconsistent cases can individually be within a 0.5 threshold of the center case).
We initially assign intuitions randomly by sampling from a uniform distribution. After running the simulation we look at the coherence of agents’ accepted case lists. We operationalize “coherence” in terms of case width: the normalized Hamming distance between the most dissimilar cases that the agent has accepted. A case width of 1 is the singleton; a case width of 0 means that the agent has at least one pairwise-inconsistent case in its ACCEPT list. As we said above (Section 3.1), pairwise inconsistency isn’t a contradiction, so strictly speaking an ACCEPT list is not inconsistent simply because it contains two pairwise inconsistent cases. Nevertheless, pairwise inconsistent cases are maximally different from another—they disagree on each feature of a case. Given that there is no representation of contradictions in our model, we find pairwise inconsistency to be a decent substitute measure of incoherence.
There are two primary considerations of how the reflective process may introduce coherence. First is agents’ initial tolerance levels. Starting with a tolerance threshold well below 0.5 is more likely to exclude pairwise inconsistent cases by the end of the process, since to include them requires more changes that increase the threshold (and possibly change the center case of the rule). Starting with a tolerance threshold above 0.5 leaves agents wide open to accepting pairwise inconsistent cases, and the process will have to work by decreasing the threshold in sufficient time to rule them out.
Second is the volume of intuitions. When there are few intuitions the deliberative procedure is called infrequently, but when the volume of intuitions is high the reflective process has more opportunities to make changes to the rule (center case or threshold). In this sense intuitions play a kind of regulative role in the reflective process.
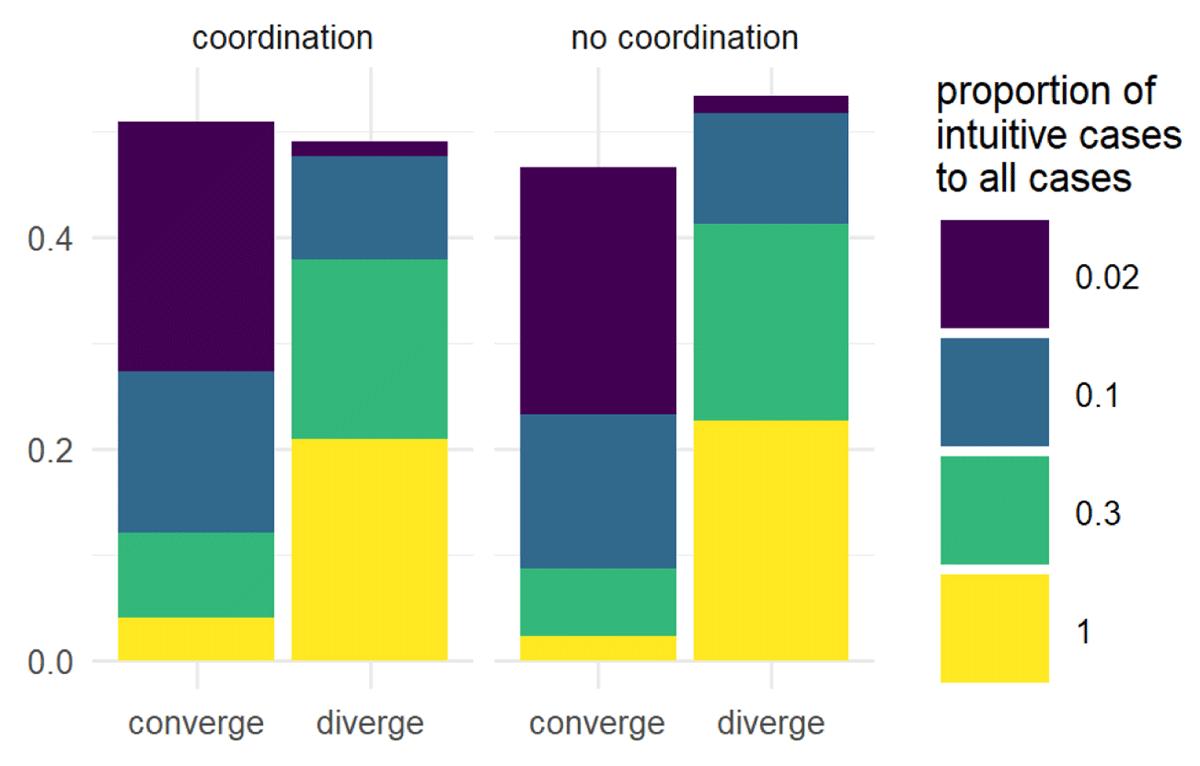
Figure 1 shows the results of these considerations. Agents with a tolerance greater than 0.5 cross the Rubicon, positioning themselves to accept cases that are pairwise inconsistent with each other (though not necessarily pairwise inconsistent with the center case). Interestingly, despite the initial permissiveness of tolerances above 0.5, increasing the volume of intuitions drives down the frequency of ending up with accepting pairwise inconsistent cases. Here, more intuitions, even without presuming systematicity, introduces coherence. However, for agents that start with tolerances below 0.5, increasing the volume of intuitions has the opposite effect, though it is small.
Conditions for accepting pairwise-inconsistent cases as a function of the ratio of cases with intuitions to all cases. Unlike tolerance levels of 0.2 and 0.4, levels of 0.6 and 0.8 enable acceptance of pairwise inconsistent cases in the extension of a rule, though this decreases as the proportion of cases with intuitions increases.
In sum, we see that agents in some conditions end up with coherent ACCEPT lists. They’re most likely to avoid endorsing pairwise-inconsistent cases when (a) being relatively impermissive (i.e., their tolerance threshold is less than 0.5) or (b) being permissive and having a lot of intuitions about cases. On reflection this result makes good sense: agents that have more cases with intuitions train themselves through modifying their center cases and tolerance thresholds. Moreover, since intuitions at the outset were assigned non-systematically, the resulting coherence is a result of agents’ strategies.29 Thus the model satisfies our reality check about tolerance and coherence.
4.2. Shared Reflective Equilibrium
Without a lot of sharing of the features listed in Section 3.4, we find that the number of reflective equilibria in our community of ten agents is on average close to ten (results not shown). In particular, we find that when agents start with a diverse set of rules, they fail to converge on even a handful of them at the end of the process. In fact, averaging across the other possible features that can be shared, the best that our community does when starting with diverse rules is worse than the worst that our community does when they start with the same rule. We thus start our presentation by supposing our agents all start with the same rule.
When agents all start with the same rule, they are also in shared pseudo reflective equilibrium, since ACCEPT and REJECT are empty (thus trivially satisfying criteria (i) and (ii) of being in reflective equilibrium) and UNCLASSIFIED is non-empty (in fact it contains all the cases to be classified). From here, we can investigate how well the process reigns in divergence from shared pseudo reflective equilibrium as agents independently make progress towards intrapersonal convergence.
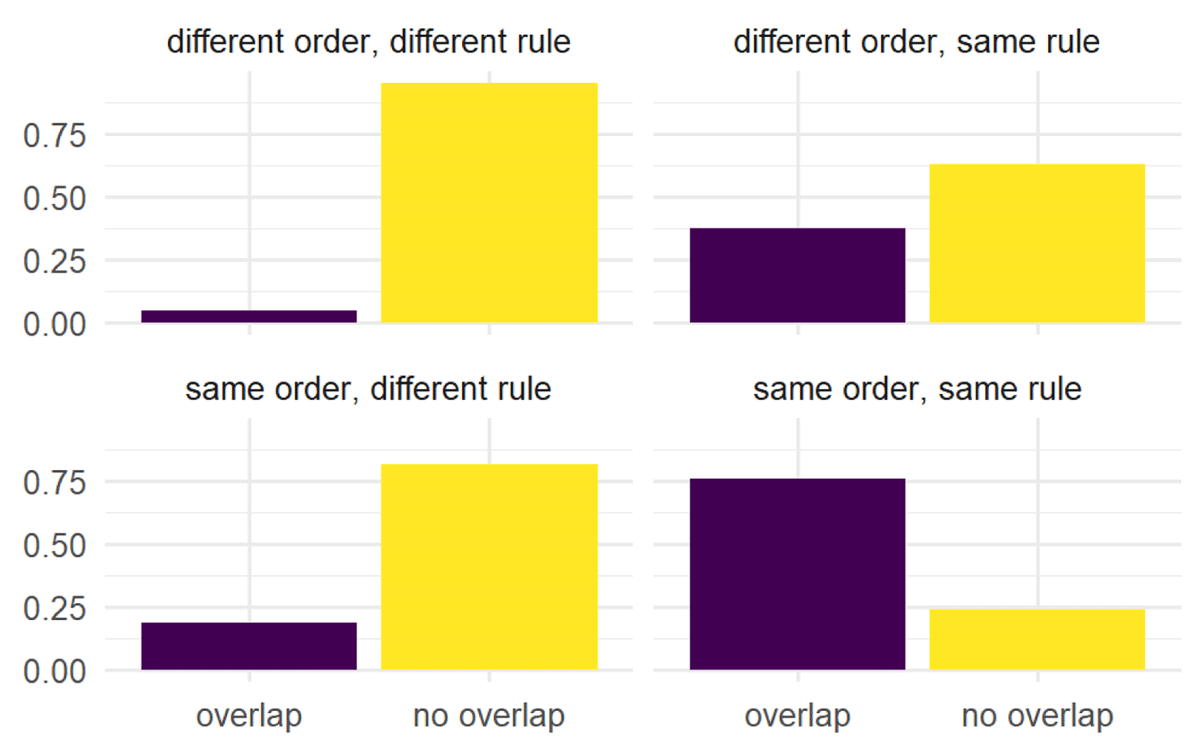
Let’s suppose that agents indirectly coordinate by agreeing on which features are more important or relevant than others. Figure 2 shows the results of these assumptions.
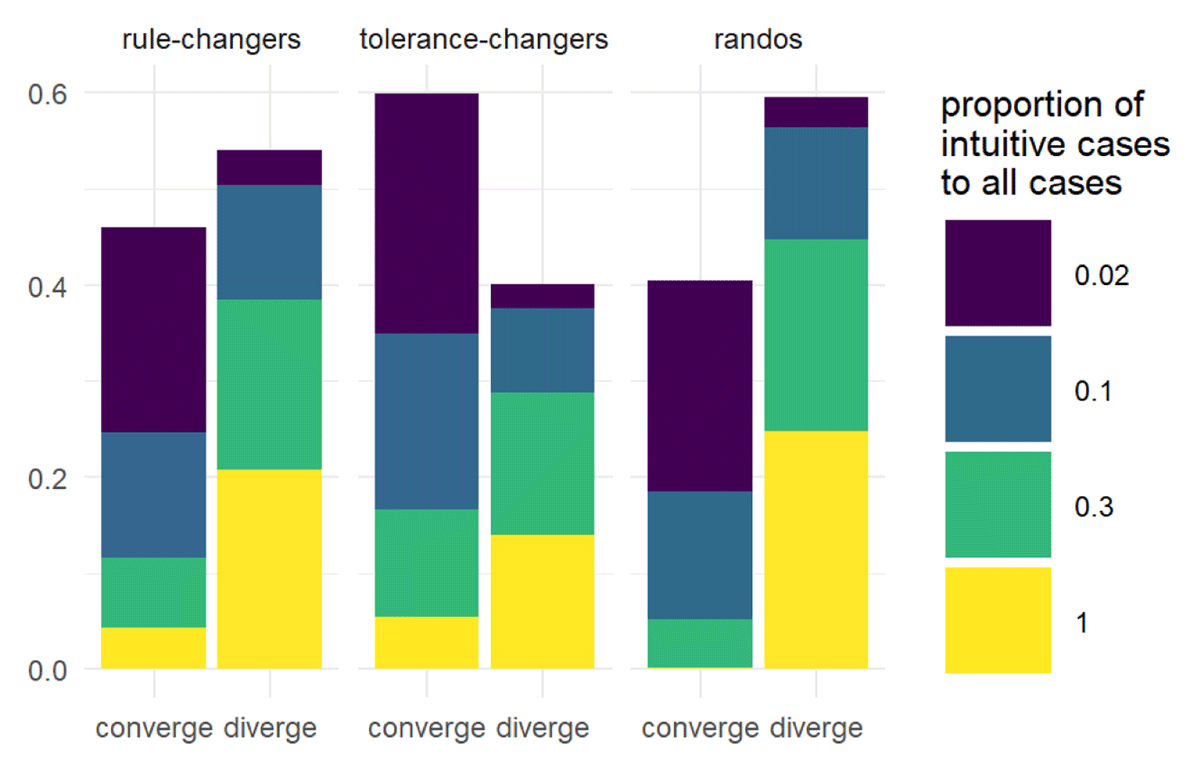
Notice that as agents have more intuitions they tend to diverge. All our results have this pattern. This reflects our previous observation: more intuitions means more opportunities to change one’s rule, changes that likely lead to divergence. And even if agents agree on a hierarchical structure of which features are more important than others, we still see a great deal of divergence.
This effect of divergence is more substantial for rule-changers than for tolerance-changers (not pictured). This is expected, given that there are more ways to change a rule (one way for each feature) than there are to change a tolerance threshold (an increase or decrease). In turn, that means there are more opportunities for rule-changers to diverge than tolerance-changers.
One can then ask, how do rule-changers compare to tolerance-changers on average, assuming still that everyone starts in shared pseudo reflective equilibrium? And how do they compare to randos, whose dispositions are random? Figure 3 illustrates the results. Notice that tolerance-changers perform better than rule-changers when it comes to converging on fewer equilibria. On reflection this makes sense. Tolerance-changers default to changing their tolerance level, so there are only 4 possible equilibria: the center case plus each of the four tolerance thresholds. Also notice that overall, our rule-changers perform better than randos at converging on a single equilibrium. But a look at the smaller three values for intuition volume30 shows that randos and rule-changers are roughly the same. It’s only when intuition volume goes high that rule-changers converge more frequently than randos.
If using the criterion of fewer equilibria, it would seem as though defaulting to a tolerance-changing strategy would be preferred. Though we don’t discuss it here, changing tolerance levels is a double-edged sword. Our analysis suggests that relying solely on changing one’s tolerance can end up with agents not accepting any cases! This happens when a tolerance-changer (a) starts with a low tolerance threshold and (b) has a run of IR cases. This causes the agent to reduce its threshold to a level so low that no case can be accepted, even when that case is a match for the agent’s center case. While this might seem odd (because it is), we find it akin to a Platonic view in which no instantiation of a Form can ever be a match to the real deal.
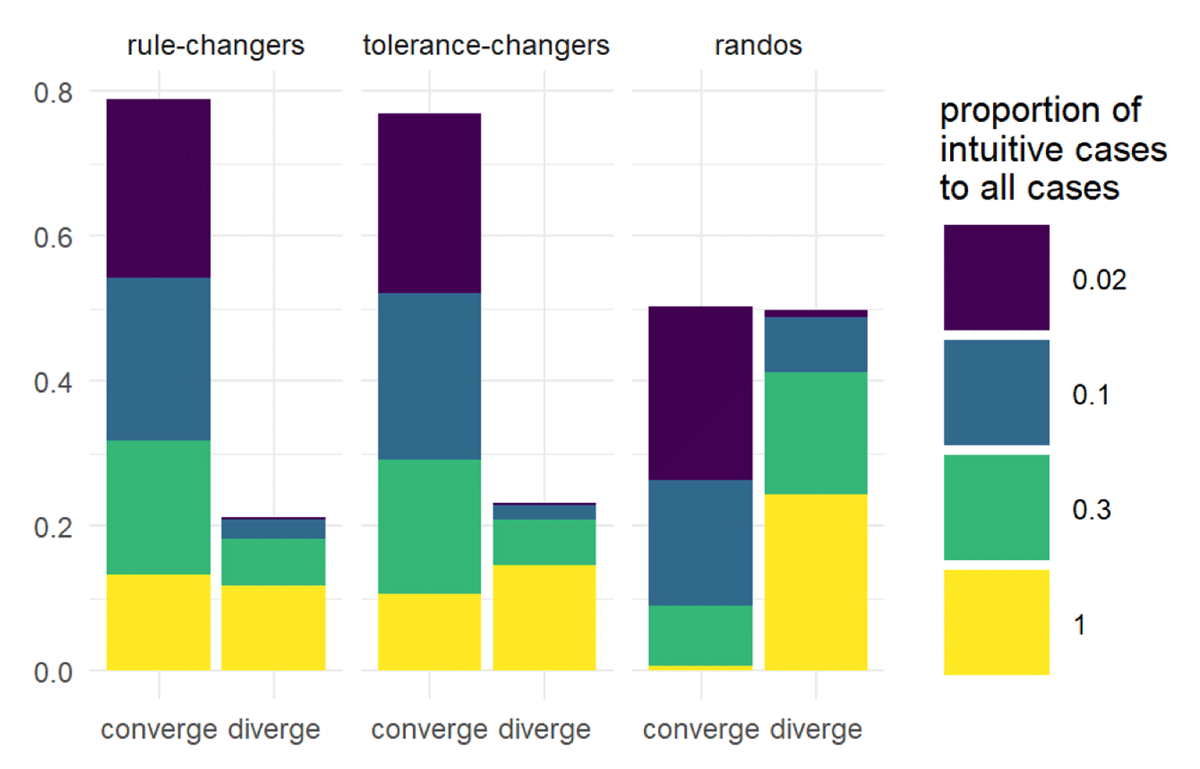
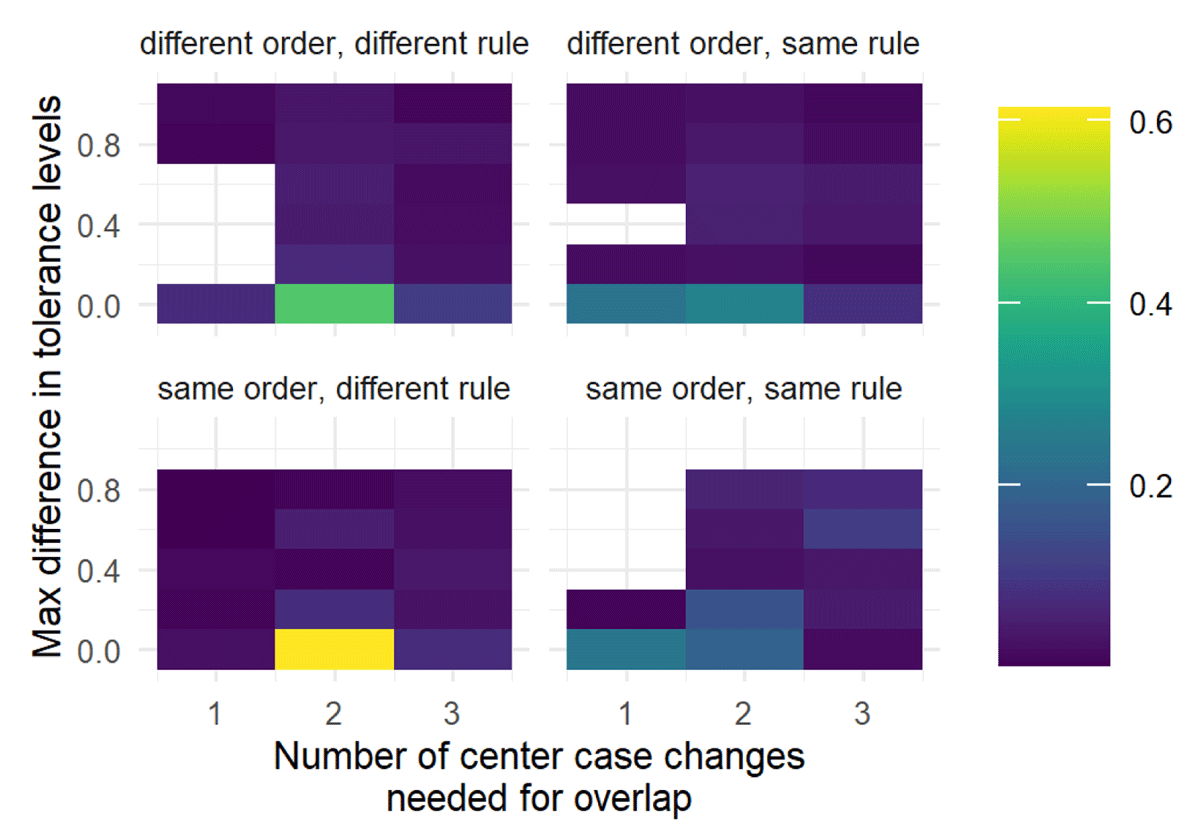
What we would ultimately like to know is whether a combination of the constraints outlined above will result in SRE, or at least few equilibria so that there are subgroups in SRE. Moreover, we would like to know if this can happen in a non-trivial way: if there are no intuitions, then trivially shared pseudo reflective equilibrium will become SRE through the mere filtering of cases. Analysis of our model suggests that the answer is “yes.” In each run of the model captured in Figure 4, every agent shares:
a starting rule,
deliberative dispositions,
indirect coordination (privileging of features),
volume of intuitions, and
ordering of cases to reflect on.
Under these constrained conditions, tolerance-changers and rule-changers do well in achieving SRE. In fact, in comparing rule-changers and tolerance-changers with randos, it’s clear that sticking with one strategy is beneficial under these circumstances.
However, achieving these conditions in the real world seems unlikely, to say the least. It would be extremely surprising if human deliberators considered the same cases in the same order, and had all the same intuitions, and agreed on the same ordering of importance of the features of cases, and have the same dispositions when deliberating over conflicts between rules and intuitions, and also happened to start with the same rule. So perhaps we’re missing something in the model up to this point. One possibility is that intuitions are already systematic and guide agents towards SRE. We turn to this possibility next.
4.3. Intuitions about a Necessary Condition
Assuming that we humans can and do achieve SRE, perhaps it is not just the method itself that contributes to this, but something about how intuitions are distributed across cases. It may be plausible that cases have a “necessary” or “key” feature that is associated with an intuition to accept those cases, or similarly a “necessary” or “key” feature associated with intuitions to reject. We have seen in the results concerning coherence that intuitions can play a kind of regulative role as the reflective procedure unfolds. So it is reasonable to expect that if the regulative role of intuitions is combined with specific sets of cases, that the reflective process would then be guided towards a specific equilibrium (or at least a small set of equilibria). In turn, such direction would make SRE more likely.
We incorporate this line of thinking as follows. For all cases agents consider, a case ending in ‘Y’ is necessary (but not sufficient) for the case to be labelled “intuitive accept.” A case’s ending in ‘N’ is necessary (but not sufficient) for the case to be labelled “intuitive reject.” We can similarly apply such labelling to any other feature of a case, and to multiple features.
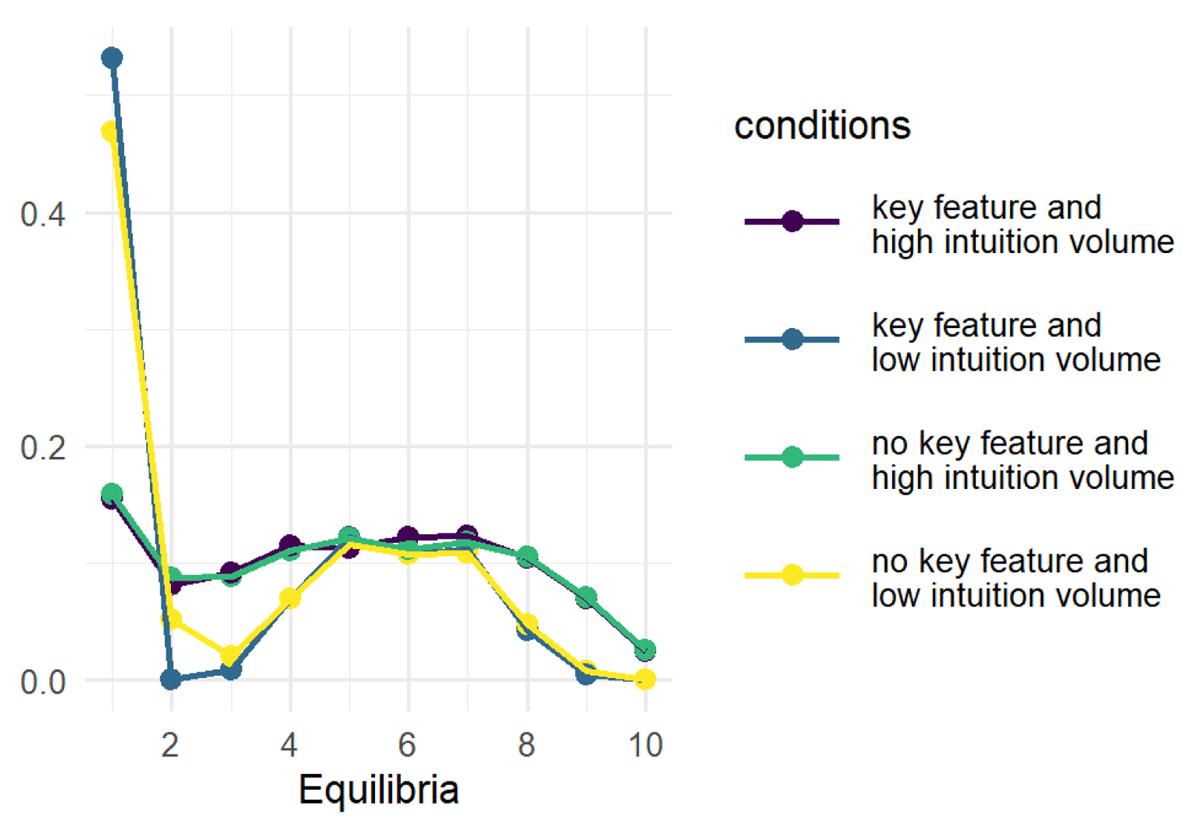
Figure 5 shows a comparison between systematically and non-systematically assigning intuitions for rule-changers and tolerance-changers for high (.5) and low (.02) volumes of intuitions. Unexpectedly, having a necessary condition makes a difference only when agents have few intuitions. But if the proportion of intuitive cases is too high—in this case, though not pictured above .1—there’s no discernible benefit to the necessary condition. Effectively, it’s as if the noise of an increasing number of intuitions impedes the signal of the necessary condition.
So when we have a systematic assignment of intuitions in conjunction with few intuitions, the number of equilibria is consistently low and there is a higher chance of achieving SRE. But as with the results we have seen generally, this benefit dissipates as agents have more intuitions. This result holds even if we add another necessary feature (not shown). The takeaway? The extent that SRE is achievable, the regulative role of intuitions in combination with systematically assigning intuitions plays a contributing but non-dominant role in attaining SRE. In order to achieve SRE, we have to go back to adding (implausible) shared features as we did previously in Section 4.2.
5. Conclusion: The Miracle of SRE?
In the introduction we asked: how much of the interpersonal convergence can be accounted for by the process that leads to intrapersonal convergence? How much did their interactions with one another aid in getting to shared reflective equilibrium? We said that answers to these questions have impacts on the broader literature on reflective equilibrium. For example, as Kelly and McGrath suggest:
[One] might very well think that it is an objectionable feature of the method of reflective equilibrium if it allows for the lack of convergence, and perhaps even radical divergence, envisaged here. According to this line of thought, a good method for investigating a given domain should lead rational inquirers who impeccably follow that method to converge in their views over time. (Kelly & McGrath 2010: 341)
We see these sorts of concerns in specific domains in philosophy. For example, Michael Smith seems to hold that a necessary condition for the truth of moral realism is that rational inquirers converge on a common moral view (see Smith 1994 and Smith 2000). Others have argued that, moral realism aside, reflective equilibrium is the only defensible method for moral matters and other subjects (see Scanlon 2003). Detractors of the method might argue that the views rational inquirers converge on are still inadequately justified because the method privileges the beliefs one holds at the beginning of inquiry.31
These discussions often take for granted that the method of reflective equilibrium converges in some way or other, but very little is said about how the implementation of the method is supposed to bring about convergence. As we have suggested above, it is not obvious that the method would converge (e.g., if fence-sitting is allowed indefinitely). And if it does, it is not clear that this convergence is of the right sort because of its contingency.
Moreover, a distinction between narrow and wide versions of the method is of little help in providing further clarification on our questions.32 A narrow version places some restrictions on which perspectives one uses to scrutinize principles and intuitions, leading to equilibria that lack full normative justification.33 In a wide version such views are further subjected to a fuller range of perspectives and extensively scrutinized, with the goal of attaining a unique equilibrium that is justified. Whatever merits a distinction between narrow vs. wide versions has, it does not help in better understanding how the method, even narrowly conceived, is supposed to bring about convergence. Further, the wide/narrow distinction is silent on the role of “descriptive” equilibria for convergence—”descriptive” in the sense that there are trivial ways to bring rules and cases into alignment that have little to no normative import. Similar concerns emerge for both versions given our focus on how the procedures bring about convergence. Consequently, we have largely glossed over the difference (but more below).
In brief, we seem to have a relatively sketchy understanding of one of the pillars of the method of reflective equilibrium that is so important in philosophy. We are not concerned here whether the method is good or bad, or the downstream consequences of whether or not there is a unique equilibrium. Rather, we are concerned with improving our understanding of the method. We are interested in understanding how the method is thought to bring about convergence, and in what senses of the term, particularly when the target system is one in which there is a dynamic interaction between the reflective process and the exploration of the universe of cases and intuitions (which differs from related target systems, as explained in Section 2).
What sorts of things do we learn, then, from our study? Go back for a moment to Kelly and McGrath (2010). They claim that intrapersonal convergence is necessary but not sufficient for interpersonal convergence. Why? Because agents with different starting points following the method impeccably aren’t guaranteed to converge. Our study confirms this.
Furthermore, Kelly and McGrath float the idea that, in addition to flawless execution of the method, starting with justified intuitions might be enough to get interpersonal convergence. To the extent that we can capture this with our model, we interpret this functionally as meaning that all agents have the same initial conditions: they have the same principle, same intuitions, and the same ordering of cases. Our study shows that even this isn’t enough to guarantee interpersonal convergence.34
What our study identifies is that the method, even when perfectly executed by agents with the same starting point and a shared body of intuitions, has room for multiple choice points that accumulate and can cause agents to diverge. This is made particularly salient in Figures 3, 4, and 5: when we increase the volume of intuitions (shown in the plots’ legends), there are more potential choice points, and in turn more divergence in the equilibria that agents land on. This appears to be the consequence of a trade-off: either agents individually risk never converging on an equilibrium at all (e.g., we allow agents to indefinitely ignore an intuition) or they implement the method to guarantee intrapersonal convergence but hinder the possibility of reaching interpersonal convergence.
In addition, our study allows us to say something more nuanced about different strategies for handling choice points. Agents that tend to default to rule-changing can better their chances of converging on a few rules by beginning with the same center case, having fewer intuitions, and coordinating with other agents for changing certain features of the center case over other features. Agents defaulting to changing their tolerance tend to do well, but they can increase their chances of ending up empty-handed by having lower tolerances and fewer intuitions.
So even flawless execution of the method with agents who share the same initial conditions isn’t guaranteed to converge on the same equilibrium because of the choice points in the method. When an agent goes back and forth, they might become more or less permissive or change their rule or shelve a case for later consideration. Each of these choices has cumulative, downstream effects. A surefire way to ensure that agents flawlessly executing the method will interpersonally converge would be to make sure they make the same decisions at these choice points. One (uncompelling) way to do that in the model is to reduce the number of choice points by reducing the volume of intuitions: fewer intuitions mean fewer opportunities to diverge. Another way is to have agents engage in some kind of collaborative effort that facilitates a mutual coordination between intrapersonal and interpersonal convergence.
For example, some systems of law seem to have codified such a coordination: judges are obliged to make their rulings as consistent as reasonably possible with previous judicial decisions on the same subject. Effectively, this means that each case that is decided by a court of law becomes a precedent or guideline for subsequent decisions. Precedence setting, then, is one way in which intrapersonal convergence can place constraints on the interpersonal process. This need not be institutionalized as a policy; it might happen de facto as a matter of course. For instance, when presenting a philosophical thought experiment, an instructor may report to the students which analysis is most widely accepted, thus nudging students to shape their intuitions or principles towards making similar classifications of that case. Another example is the role of a publication, which invites intellectual peers to consider similar reasons for accepting some conclusion. Previous publications can be used as ways of framing a debate, allowing authors some clearance to forego the considerations of some intuitions over others.35
We see an important consequence for thinking about the relationship between SRE and conceptions of wide reflective equilibrium (WRE). The way in which we have been approaching our study highlights what we think is largely unmentioned in discussions of the wide version: cognitive limitations of agents like us. The task of reaching a WRE might be too complex for any single agent to achieve, but that should not deter us from making both individual and interpersonal (collective) progress towards it. Such progress will likely involve the comparisons between (narrow) equilibria, but as a distributed process through interactions between agents. And for all we know, the progress that is made by actual inquirers might be one that is by necessity path dependent and contingent. Whether such contingency—and related “no-convergence” possibilities—undermines justificatory power is up for debate, on which we do not take sides (see Tersman 2018). Our point is that the interpersonal convergence question will require a conception of WRE that is akin to a social epistemology (if such a conception of WRE is to be had).
Alas, the model we have presented here does not have social agents. Agents do not directly interact with one another in order to share information about their rule or how they have classified cases. In some runs, they are indirectly social. For example, rule-changers act in an indirectly social way when they have an implicit agreement to “coordinate” on which sites (features) in a rule to change. But even here, they aren’t updating each other on what their center cases actually are. They merely change the same sites. This works well to keep agents constrained in the early steps of the simulations. But even if agents see cases in the same order, a small amount of stochasticity in their dispositions is enough to generate divergence. This splintering is magnified when agents see cases in different orders. Nevertheless, the indirect social interaction through agreement of a hierarchy of features does help drive down the number of equilibria under some conditions.
These simulations then suggest that having social agents—ones that actively work to communicate information about their center case and ACCEPT list—is likely of high importance. We suspect that social agents would converge on SRE much more quickly and reliably than agents in our model. As far as we can tell, it’s an open question whether sharing information would sufficiently dampen the noise of high intuition volumes. Adding sociality to our model is a project in itself that we leave for future work. An important consideration in such work would include network structures. Some agents in epistemic networks are more influential than others, either in terms of connectivity throughout the network or the weight that other agents give to the more influential agent. We suspect that, even while non-influential agents are working towards reflective equilibrium, the intervention of influential agents will drive down the final number of equilibria.
In any case, our point is this. Convergence towards a (shared) reflective equilibrium is often presumed to be attainable, perhaps as a trivial exercise that is part of a wider version of the reflective equilibrium method. It is not. How the method of reflective equilibrium brings about convergence is under-theorized and not well understood. In particular, the relation between intrapersonal and interpersonal convergence deserves much more careful analysis, to which we have made a small contribution.
Notes
- Our notion of ‘acceptance’ here is similar to Rawl’s idea of considered judgment (Rawls 1971: 47). However, an intuition about a case, prior to acceptance of the case, is issued when one is able to concentrate without distraction about the topic at hand and is stable over time. Moreover, it is reasonable to select some intuitions but exclude others, a point we return to later. We discuss the functional aspects of intuitions and acceptance later when we present our model. ⮭
- Kelly and McGrath ultimately argue that the appropriate starting point is the class of all and only those judgments that an individual is justified in holding at that time, as opposed to considered judgments. They are primarily concerned with how uniqueness of reflective equilibrium connects to claims about moral realism. We will not be concerned, at least here, with how theses about moral realism hang on how either the intrapersonal or interpersonsal questions are answered. Our focus will be on the process itself and what connections there are between the questions. ⮭
- We follow DePaul (2006) in starting with the individual case to begin sorting through the details of achieving reflective equilibrium. Understanding the process for a group of inquirers seems a hopeless task unless we begin with how individual agents do it first. ⮭
- Another way of putting this is: revising the considered judgement from believing the case falls under the rule (or doesn’t) to believing it neither does nor doesn’t fall under the rule. ⮭
- Scientists do something similar when they simultaneously theorize while also collecting (and planning to collect) new observations. See (Kelly 1996: esp. ch. 6) for an excellent characterization and study of that process and the computational constraints that come with it (see especially Chapter 6). ⮭
- Other descriptions include (Cath 2016: 214), following Scanlon (2003), who describes the third stage of achieving equilibrium as “moving back and forth between [initial principles and initial beliefs] and eliminating, adding to, or revising the members of either set until one ends up with a final set of beliefs and principles which cohere with each other.” We find similar sentiments in DePaul (2006: 20), that (narrow) reflective equilibrium is “attained by mutual adjustments of considered judgments and principles making up a moral theory.” At the very least these descriptions seem to be how the narrow version of the method of reflective equilibrium goes. Perhaps the wide version differs, but even if so it will have either as input or as a subroutine the narrow version. The (ir)relevance of the distinction between narrow and wide versions is addressed later. ⮭
- On a related note, the BBB model prima facie incorporates elements that are, arguably, not part of the method of reflective equilibrium narrowly conceived. The weighted properties in their model involve theoretical virtues, which again some might argue are not necessarily part of the principle/cases alignment process in a narrow conception of RE. This reinforces two points made in the main text: it’s not clear that there is a single conception of the target system being modeled and our aims in modeling the method are different from BBB. ⮭
- Thanks to an anonymous reviewer for bringing this point to our attention. ⮭
- For BBB, the initial theory will reflect the initial commitments, so in a different sense it’s the initial commitments that are “the beginning”. ⮭
- Similar comments go for unsupervised machine learning classification tasks. Algorithms begin with an initial hypothesis and then refine it in light of new data. ⮭
- We see this in the old saw, “one person’s modus ponens is another’s modus tollens.” ⮭
- See Weisberg (2012) for a more thorough discussion. ⮭
- For example, when modeling the swing of a pendulum one can abstract away friction and idealize the extension of the weighted bob as a point mass. Suppose we are interested in the length that the bob will swing when pulled to one side and let go. Using our model, suppose we calculate this length to be n. If we now de-idealize by imagining that the bob has extension and that its swing will not happen in a vacuum, then friction from air resistance will affect the length of the swing and our prediction of n will be off. But it will be wrong in one direction. The length of the swing in the de-idealized case will be smaller than n. ⮭
- Unless there’s something about noisy, nonideal situations that actually promotes convergence. ⮭
- See, for example, Turri, Buckwalter, and Blouw (2015). ⮭
- We use string lengths of four to illustrate the core ideas. In the simulations, all cases are of length five. ⮭
- Again, “normalized” here means we divide the Hamming distance by the length of the string, which ensures we get values from 0 to 1. ⮭
- In brief, this is because concatenation of Y/N responses to what features make up a case is not the same operation as conjunction. And even if it were, the negation of the whole string is not simply the flipping of the Y/N, but, by DeMorgan’s law, involves treating the concatenation as a disjunction. ⮭
- Thanks to an anonymous reviewer for bringing this to our attention. ⮭
- In pseduo-equilibrium, only one side of the biconditional holds: if a case is in ACCEPT, it is in the extension of the rule. ⮭
- We suppress the point that all equilibria must have UNCLASSIFIED be empty. ⮭
- By “non-trivial threshold level” we mean two things. First, the values that correspond to discrete increments in Hamming distances. For example, for strings of length 4, both thresholds of 0.25 and 0.26 will include cases within a Hamming distance of 1 from the center case, but not cases with Hamming distance 2. Second, the threshold level is neither 0 nor 1. If the tolerance threshold is 0, then the extension of every center case is empty. If the threshold is 1, then the extension of every center case is the universe of cases. ⮭
- For strings of length n, there are n + 1 total equilibria, but this includes two trivial thresholds: 0 and 1. Removing them gives us n – 1 non-trivial thresholds. ⮭
- Similar comments go for previously rejected cases and the complement of the principle’s extension. ⮭
- If tolerance-changers and rule-changers cannot update their rule to accommodate an incoming case, that case is put on to the POSTPONE list and its intuition assignment replaced with “NI.” ⮭
- Recall that “IA” is a label that represents that this case should be intuitively accepted. ⮭
- To illustrate: given the rule <YYYN, 0.25>, one must accept both YYYY and YYNN. So if an agent is faced with the intuitions IA-YYYY and IR-YYNN, and they are not willing to change their rule, they must ultimately remove the intuition label from IR-YYNN in order to make reflective equilibrium possible. ⮭
- As Quine (1951) tells us. ⮭
- Further analysis, not included here, suggests that particular agent strategies—rule-changing, tolerance-changing, or random choice—make little difference for coherence. ⮭
- We use ‘intuition volume’ as a short-hand for “proportion of intuitive cases to all cases.” ⮭
- See Kelly and McGrath (2010) for a discussion of such arguments from detractors. ⮭
- See Daniels (1979) for a discussion of the difference. Some have argued that the difference is overstated (Holmgren 1989). ⮭
- We use the indefinite article intentionally because there is no consensus on what the narrow version is (and similarly a wide version). We say more below. ⮭
- At least not for our target system. Perhaps it might be under suitable conditions and trade-offs in the BBB model we discussed in Section 2, but that is not for us to say. ⮭
- Interestingly, what this means is consistent with extant commentary on the use of intuitions in philosophical methodology. Turri (2016), for example, notes that the famous Gettier paper was less of a good experiment in soliciting a reader’s intuition about a case and more an instance of Gettier telling the reader what their intuition should be about the case. Consequently, the resulting consensus surrounding the case as a counterexample to the traditional account of knowledge as justified true belief is questionable and requires more careful empirical study. Whether or not the Gettier consensus is questionable, we share the presupposition that if individuals influence one another in their intuitions while they are deliberating, that this would help drive communities towards consensus—in our case, SRE. ⮭
Acknowledgments
Both authors are grateful for feedback from audiences at the 72nd annual Northwest Philosophy Conference, Reflective Equilibrium: 51 Years After A Theory of Justice, and the Philosophy of Science Association’s 28th biennial meeting.
References
1 Beisbart, C., G. Betz, and G. Brun (2021). Making Reflective Equlibrium Precise: A Formal Model. Ergo, 8(15), 441–72. http://doi.org/10.3998/ergo.1152
2 Brun, Georg (2014). Reflective Equilibrium Without Intuitions? Ethical Theory and Moral Practice, 17(2), 237–52.
3 Cath, Yuri (2016). Reflective Equilibrium. In Herman Cappelen, Tamar Szabo Gendler, and John Hawthorne (Eds.), The Oxford Handbook of Philosophical Methodology (213–30). Oxford University Press.
4 Daniels, Norman (1979). Wide Reflective Equilibrium and Theory Acceptance in Ethics. The Journal of Philosophy, 76(5), 256–82.
5 Daniels, Norman (2020). Reflective Equilibrium. In Edward N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy (Summer 2020 ed.). https://plato.stanford.edu/archives/sum2020/entries/reflective-equilibrium/
6 DePaul, Michael R. (2006). Balance and Refinement: Beyond Coherence Methods of Moral Inquiry. Routledge.
7 Goodman, Nelson (1983). Fact, Fiction, and Forecast. Harvard University Press.
8 Holmgren, Margaret (1989). The Wide and Narrow of Reflective Equilibrium. Canadian Journal of Philosophy, 19(1), 43–60.
9 Kelly, Kevin T. (1996). The Logic of Reliable Inquiry. Oxford University Press.
10 Kelly, Thomas and Sarah McGrath (2010). Is Reflective Equilibrium Enough? Philosophical Perspectives, 24, 325–59.
11 Quine, W. V. O. (1951). Two Dogmas of Empiricism. Philosophical Review, 60(1), 20–43. http://doi.org/10.2307/2266637
12 Rawls, John (1971). A Theory of Justice. Harvard University Press.
13 Scanlon, T. M. (2003). Rawls on Justification. In Samuel Freeman (Ed.), The Cambridge Companion to Rawls (139–67). Cambridge University Press.
14 Smith, Michael (1994). The Moral Problem. Blackwell.
15 Smith, Michael (2000). Moral Realism. In Hugh LaFollete (Ed.), The Blackwell Guide to Ethical Theory (15–37). Blackwell.
16 Tersman, Folke (2018). Recent Work on Reflective Equilibrium and Method in Ethics. Philosophy Compass, 13(6), e12493.
17 Turri, John (2016). Knowledge Judgments in “Gettier” Cases. In J. Sytsma and W. Buckwalter (Eds.), A Companion to Experimental Philosophy (337–48). Wiley.
18 Turri, John, Wesley Buckwalter, and Peter Blouw (2015). Knowledge and Luck. Psychonomic Bulletin & Review, 22 (2), 378–90.
19 Veit, Walter, Jonathan Anomaly, Nicholas Agar, Peter Singer, Diana S. Fleischman, and Francesca Minerva (2021). Can ‘Eugenics’ Be Defended? Monash Bioethics Review, 39, 60–67.
20 Weisberg, Michael (2012). Simulation and Similarity: Using Models to Understand the World. Oxford University Press.
Appendix: Additional Fine Features
While agents tend to diverge if given their druthers, there might also be substantial overlap in rules. Two rules ‘substantially overlap’ if:
they share a center case,
they have the same tolerance level, and
they have a normalized Hamming distance of at least .6 (i.e., no more than two sites where the center cases differ.
We saw previously that two variables of importance for convergence are sameness of starting rule and sameness of case order. This gives us a 2x2 case for comparing overlap, seen in Figure 6.
We see here that our agents are much more inclined to not have substantial overlap in their rules. In comparing the bottom right panel with the upper right and bottom left, we see that starting with the same rule does more work in achieving overlap that seeing cases in the same order.
In the four settings of same/different case ordering and same/different initial rules, beginning with the same initial rule and same case ordering is a boon to having substantial overlap but far from guaranteeing it. In fact, more often than not, we see that rules tend not to substantially overlap
But we can go to an even finer grain. Consider Figure 7. The x-axis tells us the maximum number of changes agents would have to make to have substantial overlap on a center case. There might be agents that are closer in agreement, but there are none that are further. The y-axis indicates the maximum difference in tolerance levels for the agents in a given run of the model. A value of .4 means that the maximum difference in tolerance thresholds among that set of agents is .4, though there might be two agents with smaller differences in thresholds.
Figure 7 reinforces the moral of the story: having the same initial starting rule is helpful for convergence or substantial overlap, particularly when agents see cases in the same order. We see, though, that it’s not a matter of near-misses. If that were the case, there would be bright spots around bottom-left of each facet. Instead, values seem more broadly distributed. One exception is the same-order-different-rule condition, in which a majority of the runs ended with the furthest agent being two matches away from substantial overlap. While this is noteworthy, it’s worth keeping in mind that this means the maximum difference in center cases is found out of 5 in these runs, meaning they shared one site.