1. Introduction
Over twenty years ago Christopher Hitchcock (2001b) told his fellow philosophers of causation that ‘we live in exciting times’. The formal work on structural equations modelling, born from econometrics, epidemiology and artificial intelligence, was beginning to be merged with philosophical theorising about causation. Structural equations modelling has helped reveal previously hidden ambiguities in our causal concepts (Hitchcock 2001a), helped provide a basis upon which to derive important theorems about causal structures (Pearl 2009), assisted in a rigorous definition of ideal intervention, helped us more clearly consider the logical properties of causal relations (Hitchcock 2001b) and helped us define notions like ‘actual causation’ (Halpern & Pearl 2001; Pearl 2009; Woodward 2003). And structural equations techniques are no less relevant to the literature today, as any cursory survey of debates surrounding causal analysis, constitutive explanation or causal overdetermination/exclusion is likely to reveal.
It is perhaps strange, then, that the techniques of structural equations modelling have still to find their way into the debate over analysis of dispositions. After all, dispositions are widely taken to be causally defined. It has been remarked that the stimulus-disposition-manifestation relation ‘is very much the same sort of thing as the causal relation’ (Bird 2010: 166), that ‘the notions of power or disposition are already causally laden notions’ (Mumford & Anjum 2011: 7), and even that ‘dispositions are causal-role occupiers by conceptual necessity’ (Mumford 1998: 77). More specifically, ‘in the dispositions/powers literature, it is common to assume that a manifestation is an effect of a disposition being activated’ (McKitrick 2010: 73). If this is all true, then it can appear a salient omission that structural equations techniques have not yet been brought to bear on the tricky issue of dispositions’ analysis.
The present article aims to rectify this lacuna, and not without some significance. After providing the basic requirements for competency with structural equations modelling techniques (§2), I’ll move on to demonstrate (§3) how they can be employed in a ‘Simple Structrual Equations Analysis’ (SSEA) that has the ability to deal with three problem cases a number of extant accounts face, including the infamous ‘Simple Counterfactual Analysis’. These problem cases include dispositional tricks, conjunctive quantitative multi-track dispositions and dispositional degrees. I’ll then (§4) aim to assuage an immediate concern that the proposed analysis invokes too many counterfactuals in the analysis of dispositions to be plausible. Following this, I’ll seek to modify the analysis in two important respects. The first is in response to the (well-known) problems of masks and of alters, as well as another novel problem of alternative causes. After describing these problems and proposing a modification to deal with them (§5), I’ll then address the issue of whether or not the modification leads to a lack of informativeness in the analysis (§6). The second modification I’ll propose is in response to the problem of mimickers (§7), in which I’ll introduce to the analysis a term which makes reference to underlying processes. The final result is an analysis schema (SEA*) that has the ability to deal with a significant variety of problem cases which analyses of dispositions have been historically tested against. I conclude the article with some commentary on problems not addressed by the new analysis (§8).
Before getting underway, let me flag some of the loose talk I’ve permitted myself in what follows. The heritage of the debate concerning analysis of dispositions is one engaged in the analysis of dispositional expressions, for example, ‘x is fragile’, ‘x is disposed to break when struck’ (Carnap 1936; Ryle 1949; Storer 1951). Over subsequent years, however, talk of dispositional expressions has often been replaced with talk of dispositions themselves, for example, fragility, or the disposition to break when struck. This ‘ontic shift’ may be, in part, due to a growing scepticism about the idea of conceptual analysis as a feasible philosophical objective, or perhaps due to an increasing permissiveness to more metaphysically loaded questions. Whatever the reason, by the time Lewis offered his (1997) contribution it was seen as acceptable to cast the whole discussion directly in terms of the analysis of dispositional properties.
Despite the shift, it should be emphasised that a commitment to dispositions (dispositional properties) need not be understood as a commitment to anything more than ‘predicatory properties’ (Bird 2016; 2018). At least, for the sake of what follows, in talking of dispositions I intend to remain uncommitted over whether dispositions ‘really exist’ (in as full a sense of the phrase as one might like) or whether talk of the analysis of such properties is really just a façon de parler, a convenient shorthand for the analysis of what objects or systems are like when we can truly describe them in dispositional terms.
This ontic shift in locution simplifies discussion considerably. But it also raises new questions about what the role of analysis might be. Traditionally, to provide an analysis of dispositional expressions was to provide a schematic biconditional on which one side (by convention, the left) is replaced by the statement that some named sentence incorporating a dispositional expression is true and the other side by whatever conditions make the biconditional true of conceptual necessity.1 When we reframe the analysis in terms of the sufficient and necessary conditions for something to exemplify a dispositional property, we are no longer constrained to reveal something about what mastery of the dispositional concepts employed in the analysis consists in, and so can draw on technical vocabulary and expressions that are unlikely to be in the minds of most speakers using dispositional language. Instead, one might take the right-hand side of such analyses to provide the grounds for the exemplification of the corresponding dispositional property (perhaps in terms of non-dispositional properties). Alternatively, one might treat such an analysis as stating only a ‘necessary equivalence’ (Bird 2007: 43) between the exemplification of a disposition (which may be a real power) and some other kind of modal fact, which may itself be explained by the disposition. I will here refrain from making a choice over these options. I do, however, assume that, like their linguistically oriented predecessors, analyses of dispositions should be comprehensible, expressible, and theoretically illuminating.
2. Structural Equations Modelling
A Structural Equation has the form B(y) ⇐ f(A1(X1),…, An((x2)) and expresses an asymmetric relationship of dependency by the left-hand variable property B of some particular y on some function f over the right-hand variable properties A1 of x1, A2 of x2, …, and An of xn (the particulars need not be distinct).2 A structural equation therefore incorporates within it lots of counterfactual information about how y would behave, counterfactuals of the form: if it were that A1(x1)=a1 &…& An(xn)=an (i.e., each variable in the right-hand side were to take some specific value) then it would be that B(y) = b. Indeed, they provide a counterfactual for every combination of values (potentially, within some predefined range) for the right-hand variables. Thus structural equations are able to capture a wealth of behavioural dependencies exhibited by an object or system incredibly concisely.
Structural equations are bread and butter for contemporary causal analysis in science and philosophy of science. Causal results and hypotheses are typically expressed, not in terms of structural equations directly, but in terms of structural equations (or simply ‘causal’) models, an ordered pair (V, E) comprising a variable set V and structural equations set E for which every variable in V is either ‘endogenous’, and so on the left-hand side of at most one equation in E (i.e., being dependent on some other variables in the model), or else is ‘exogenous’ (having its value determined by factors outside of the model). Associated with any causal model is a causal graph where the variables in V are nodes and directed edges (arrows) lead from one variable A to another B just in case A features in the right-hand side of a structural equation in which B is the left-hand variable (see below for examples).
Below, I will make use of causal models and structural equations to describe the causal relationships involved when dispositions and their stimuli are in play.3 These will include ‘stimulus variables’, ‘manifestation variables’ and ‘disposition variables’, which take values ranging over whether (and to what degree) an object is stimulated, manifests and has a disposition, respectively.
For a simple example, let’s consider the causal model MODEL 1 concerning causal relationships relevant to the behaviour of an object which has the dispositional property of buoyancy. Relevant details can be captured in the following table.
| Table for MODEL 1 | |||
| Variables | Structural Equations | ||
| Symbol | Possible values | Interpretation | |
| BU(x) | 1 | x is buoyant | (Exogenous) |
| 0 | x is not buoyant | ||
| L(x) | 1 | x is placed in a liquid | (Exogenous) |
| 0 | x is not placed in a liquid | ||
| RI(x) | 1 | x rises | RI(x) ⇐ BU(x) × L(x) |
| 0 | x doesn’t rise | ||
Accordingly, the model is captured by the following pair.
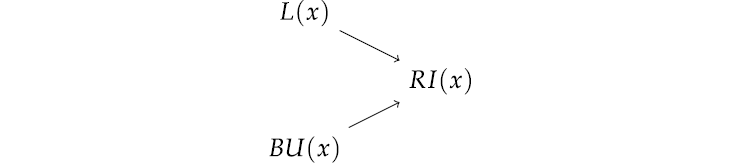
MODEL 1. ({BU(x),L(x),RI(x)},{RI(x) ⇐ BU(x)×L(x)}).
The associated graph is displayed in Figure 1.
Let’s take a look at how such a causal model bears on the discussion of analysis of dispositions. In contemporary debate, the central foil against which most recently defended analyses have been put forward is the so-called ‘simple counterfactual analysis’ (SCA), which has the following schema.4
SCA. For all x, Dx if and only Sx □→ Mx,
where ‘D’ is to be replaced by a term which denotes a qualitative disposition, ‘S’ by a term denoting a relevant stimulus, ‘M’ by the specification of a manifestation and ‘□→’ is the counterfactual conditional. A plausible SCA for buoyancy would therefore be the following.
SCA4BUOY. For all x, x is buoyant if and only if, were x placed in a liquid, x would rise.
If we take the structural equation in MODEL 1 to be a general characterisation of causal relationships any object x whatsoever is involved in (i.e., regardless of whether it is or isn’t buoyant, in a liquid, or rising) then under plausible assumptions, MODEL 1 entails the truth of SCA4BUOY. For it entails that if something x were buoyant (BU(x) = 1) and were immersed in a liquid (L(x) = 1) then it would rise (RI(x) = 1), whereas if x were not buoyant (BU(x) = 0) and were immersed in a liquid (L(x) = 1) then it would not rise (RI(x) = 0). Under the assumption that possible worlds are strongly centred on the actual world (so that the actual world is the closest possible world in which any true proposition is true) then the biconditional in SCA4BUOY follows.
This entailment gives us the first clue as to how Structural Equations Models (SEMs) might prove relevant to the analysis of dispositions. Of course, few today endorse SCA as the correct schema for analysing dispositions. Instead, SCA has often been used somewhat like a template from which to develop more sophisticated analyses of dispositions (e.g., Bird 2007; Hüttemann 2004; Lewis 1997). In what follows, I first (§3) develop a ‘Simple Structural Equations Analysis’, which capitalises on the entailment of SCA’s conditional while at the same time improving on it by virtue of the fact that structural equations also supply a richer set of conditionals than SCAs. As I show, this allows the analysis to avoid a number of problem cases that SCA can’t deal with. Later on (§5 and §7) I use this new simple analysis as a template to develop further modifications which allow the resulting structural equations analysis to deal with even further problem cases.
3. A Simple Structural Equations Analysis
The basic idea behind my ‘Simple Structural Equations Analysis’ (SSEA) is to draw on the counterfactual implications encoded in the structural equation which features in a model for instances of the disposition that include the disposition variable itself alongside the stimulus variable and manifestation variable (as in MODEL 1). The general schema looks as follows.
SSEA. For all x, D(x) = d if and only if M(x) ⇐ f(S1(y1), …, Sn(yn)).
Unlike SCA, SSEA concerns itself with variables rather than qualitative predicates both in the analysans and analysandum. What gets analysed in instances of SSEA is the assignment of some value d (e.g., 1) to a disposition variable D(x) (e.g., BU(x)) for any object x. And the analysans of instances of SSEA are explicit structural equations relating a manifestation variable M(x) (e.g., RI(x)) to a potential multiplicity of explicit stimulus variables S1(y1),…,Sn(yn) (e.g., L(x)).5
Let’s start by seeing how this works with our go-to example of the disposition of buoyancy. Since being buoyant is qualitative (i.e., a dispositional property which something either has or doesn’t have), we approach this by interpreting the disposition as the value assignment of a dichotomous variable, so that an analysis of the disposition is treated as equivalent to an analysis of the variable assignment BU(x) = 1. Assuming MODEL 1 captures the causal relationships involving the disposition, stimulus and manifestation variables characteristic of instances of buoyancy, the analysis then proceeds as follows.
SSEA4BUOY. For all x, BU(x) = 1 if and only if RI(x) ⇐ L(x).
Unlike the the structrual equation in MODEL 1, the structural equation employed in SSEA4BUOY does not feature the disposition variable BU(x). Obviously, it would be problematic for the analysis to do so, since it is that very variable (or rather its assignment to a particular value) which is to be analysed. Nevertheless, we can see that if MODEL 1 is accurate, then if it were the case that BU(x) = 1 it would then be that RI(x) ⇐ L(x), and if it weren’t the case that BU(x) = 1 it wouldn’t be the case that RI(x) ⇐ L(x). Hence, under the assumption that worlds are strongly centred, and that BU(x) and L(x) are causally independent, then BU(x) = 1 if and only if RI(x) ⇐ L(x). In other words, the structural equation in MODEL 1 reduces to that of SSEA4BUOY given that BU(x) = 1 under those assumptions.
As we saw in §2, the structural equation in MODEL 1 predicts the same counterfactual that features in the analysans SCA4BUOY, namely the ‘positive’ counterfactual that any buoyant object x would rise were it immersed in a liquid:
POSITIVE. L(x) = 1 □→ RI(x) = 1
Any problems for the necessity of the analysans in SCA4BUOY will therefore also be a problem for the necessity of the analysans in SSEA4BUOY. This includes the problem of masks and reverse-cycle finks. Insofar as SSEA is an improvement on SCA, it is therefore not an improvement by addressing these worries, which will be addressed instead by further modifications to SSEA, considered in §5 and §7. However, the structural equation of MODEL 1 predicts more than this. Specifically, (at least, when RI(x) and L(x) are dichotomous) the structural equation in SSEA4BUOY encodes a further ‘negative’ counterfactual.
NEGATIVE. L(x) = 0 □→ RI(x) = 0
This additional consequence of the analysis is atypical and warrants some discussion. In the following two subsections I show how the scope to encode further counterfactuals, such as NEGATIVE, provides instances of SSEA with the means to avoid two problems which face instances of SCA, viz., dispositional tricks and conjunctively quantitative multi-track dispositions. In a third subsection I then demonstrate how formulating dispositions’ analyses in terms of value assignments of dispositional variables provides SSEA with the means to address a further issue that SCA has been criticised for failing to, viz., dispositional degrees.
3.1 SSEA and Tricks
We begin by looking at the relatively underexplored problem of dispositional ‘tricks’. Like the better-known problem of mimickers (see §7), dispositional tricks occur when circumstances are such that objects that do not have some disposition (and that continue not to have it) behave as though they did. However, unlike mimickers, tricky objects do not behave in a deceptive way in response to the imitated disposition’s stimulus, but rather because that is how they are liable anyway to behave due to independent circumstances (Contessa 2016). For instance, something non-buoyant can manifest the same property as that associated with being buoyant, namely rising in a liquid, if (for independent reasons) it’s being pulled upwards by a fishing line. We can capture this in a new causal model, TRICK MODEL, characterised in the following way.
| Table for TRICK MODEL | |||
| Variables | Structural Equations | ||
| Symbol | Possible values | Interpretation | |
| BU(x) | 1 | x is buoyant | (Exogenous) |
| 0 | x is not buoyant | ||
| L(x) | 1 | x is placed in a liquid | (Exogenous) |
| 0 | x is not placed in a liquid | ||
| FI(x) | 1 | x is pulled up by a fishing line | (Exogenous) |
| 0 | x is not pulled up by a fishing line | ||
| RI(x) | 1 | x rises | RI(x) ⇐ BU(x) × L(x) + FI(x) – BU(x) × FI(x) × L(x) |
| 0 | x doesn’t rise | ||
Accordingly, TRICK MODEL is captured by the following pair.
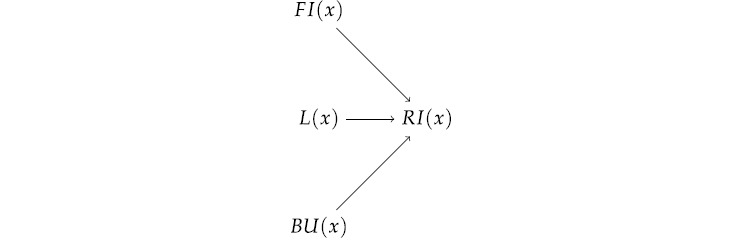
TRICK MODEL. ({BU(x),L(x),FI(x),RI(x)},
{RI(x) ⇐ (BU(x) × L(x) + FI(x) ₋ BU(x) × FI(x) × L(x))}).
The associated graph is displayed in Figure 2.
TRICK MODEL entails counterfactuals which are inconsistent with SCA4BUOY. In particular, it entails that even if x were not buoyant (BU(x) = 0), it could be rising anyway if it were being pulled up by a fishing line (FI(x) = 1). In that case the counterfactual that if x were placed in a liquid (L(x) = 1) it would rise (RI(x) = 1) would be true. This means that there are possible circumstances in which the right-hand side of SCA4BUOY is true but the left-hand side is false.
An analysis would avoid this problem is if there were an additional counterfactual in the analysans which establishes, not only that something is buoyant only if it would rise were it placed in a liquid, but also only if it would not rise were it not placed in a liquid, that is, the problem is avoided by an analysis that renders the manifestation counterfactually dependent on the stimulus. Since the rising of an object being pulled up by a fishing line is not counterfactually dependent on being immersed in a liquid, such an analysis would avoid the problem of dispositional tricks. But this is just to say that the analysis for buoyancy should encode both POSITIVE and NEGATIVE. That is, the very counterfactuals encoded in the structural equation which features in SSEA4BUOY.
In general, instances of SSEA do not suffer from the problem of tricks because they require that manifestations be counterfactually dependent on stimuli when a disposition is instantiated. In the case where the variables are dichotomous, this dependency will correspond to two counterfactuals encoded in the structural equation of the analysans (one positive, one negative). In the case where variables are not dichotomous, the dependency will correspond to a greater number of counterfactuals, as demonstrated in consideration of the problem case discussed in the following subsection. The imputed counterfactual dependency aligns the relationship between stimulus and manifestation of disposed objects established by instances of SSEA much as naive counterfactual theories of causation understand the relationship between causes and effects. This suggests the schema will be prone to an analogue of the problem of pre-emption, and indeed it is. Luckily, this ‘problem of alternative causes’ has structural similarities with the problems of masks, and can be dealt with by the same modification to SSEA, as I demonstrate in §5.
3.2 SSEA and Conjunctive Quantitative Multi-Track Dispositions
So far we have been considering models in which the stimulus and manifestation of a disposition is an all or nothing affair. But disposed objects can also be stimulated to different degrees, and in response the disposed object may manifest that disposition to different degrees. For instance, a buoyant object can be placed in a liquid of greater or lesser density and rise faster or slower in response. Arguably, the proportionality between density of the liquid and speed of rising is constitutive of the property of buoyancy. That is, something would not be buoyant if it did not rise in a liquid proportionally to the a liquid’s density. This proportionality suggests that buoyancy should be analysed in more complex terms than a simple ‘single-track’ relationship between being placed in a liquid and rising. Instead, it should be analysed in terms of a conjunction of multiple relationships relating varying degrees of density of the liquid and the speed of rising. Hence, we may call such dispositions ‘conjunctive quantitative multi-track dispositions’.6
We can capture buoyancy, so understood, with a re-interpretation of the variables in MODEL 1 and an adjustment to its sole equation. Let the stimulus and manifestation variables L(x) and RI(x) be assigned a continuum of possible values so that they are no longer dichotomous but take values along a range of densities and speeds of rising (respectively). There are various ways of doing this, but perhaps the most straight forward is to let L(x) = 0 be that x is in a region of density lower than that of any liquid and to let RI(x) = 0 be that x is not changing altitude. Then, for some constant c, the following MULTI-TRACK MODEL will capture buoyancy’s quantitative multi-track nature.
MULTI-TRACK MODEL. ({BU(x),L(x),RI(x)},{RI(x) ⇐ c × BU(x) × L(x)})
Since the structural equation in MULTI-TRACK MODEL concerns non-dichotomous variables its encoded counterfactuals are far more numerous than those of MODEL 1. Whereas MODEL 1’s equation encodes four counterfactuals (for each combination possible values to the antecedent variables BU(x) and L(x)), the equation in MULTI-TRACK MODEL encodes infinite counterfactuals (due to the infinity of possible values of L(x)). In this sense MULTI-TRACK MODEL represents buoyant objects in a much more fine-grained way (cf. Aimar 2019).
Now, MULTI-TRACK MODEL does not pose trouble for SCA4BUOY understood only as a possible instance of buoyancy. But it does pose trouble if its more fine-grained detail is taken to be definitive of buoyancy, as suggested above. That’s because SCA4BUOY entails only that, if x were buoyant (BU(x) = 1) and were placed in a liquid (effectively, L(x) = l, for some l ∈ ℝ+), it must rise at some or other speed (RI(x) = r, for some r ∈ ℝ). But if MULTI-TRACK MODEL is to replace MODEL 1 as a representation of the causal behaviours of objects in general, with regard to their state of buoyancy, any buoyant object x (BU(x) = 1) must give rise to a proportional response in speed of rising RI(x) to the density of the liquid L(x). Assuming it is possible that some non-buoyant object could rise with a speed that is not proportional to the density of liquid it is placed in, it is therefore possible for the right-hand side of the biconditional in SCA4BUOY to be true while the left-hand side is false. If SCA4BUOY is exemplary of the general form of analysis, this spells trouble for SCA in general.
By contrast, SSEA readily affords an analysis which takes conjunctive quantitative multi-track dispositions into account. All we have to do is replace in our analysis the structural equation implied by MODEL 1 (and fixing the value for BU(x)) with the corresponding structural equation implied by MULTI-TRACK MODEL:
SSEA4BUOY(MT). For all x, BU(x) = 1 if and only if RI(x) ⇐ c × L(x).
It’s worth pausing to emphasise the importance of this improvement over SCA. While it may remain contentious whether or not something is buoyant only if the speed of its rising in liquids is proportional to the liquid’s density, there clearly are dispositions that are conjunctively quantitatively multi-track in the way captured by fine-grained models of a form similar to MULTI-TRACK MODEL. These are the dispositions—or ‘capacities’ (Cartwright 1989; 1999)—we find in the quantitative sciences. Examples include a population’s intrinsic growth rate, an environment’s carrying capacity, a material’s specific heat capacity and a commodity’s price elasticity. Each of these is a disposition associated with a characteristic equation (respectively, the Malthusian growth model, the Logistic growth models, the equation for material heat absorption and the equation for price elasticity) that helps define causal models representing the relevant disposition as a conjunctive quantitative multi-track disposition. For instance, the specific heat capacity of a material is represented in the following HEAT MODEL, whose sole equation is an instance of the equation for heat absorption, with constant c substituted for the variable for specific heat capacity and interpreted in structural terms, where the stimuli are the heat absorption Q(x) and mass of the material M(x), and the resultant manifestation is change in the material’s temperature ΔT(x).7
HEAT MODEL. ({Q(x),M(x),ΔT(x)},{ΔT(x) ⇐ c × Q(x) × M(x)})
SCA is clearly incapable of providing the fine-grained detail necessary to analyse having specific heat capacity c. That’s because its single counterfactual prevents it from providing sufficient detail about the correspondences between changeable values of the stimulus variables (Q(x) and M(x)) and manifestation variable ΔT(x). By contrast, the fineness of grain of SSEA is limited only to how fine-grained structural equations can be, which is exactly as fine-grained as the numerical equations of quantitative science.
3.3. SSEA and Dispositional Degrees
Of course, it’s not only the stimulus and manifestation that come in degrees. A disposition itself can come in degrees too. For instance, one material can have a different specific heat capacity to another. That’s why it is a variable for heat capacity C(x) that typically features in the equation for heat absorption rather than a constant. Similarly, environments have different carrying capacities from each other for certain organisms, and commodities have different price elasticities. Also, one object x can be more buoyant than another y, meaning, roughly, that for any density L(x) of the liquid x is immersed in, x rises faster than y when placed in it.
As with degrees of stimulus, dispositional degrees are easily captured in causal models by further adaptation of MODEL 1. This time, as well as assigning the variables L(x) and RI(x) a continuum of possible values, we also do the same for the disposition variable BU(x) (where BU(x) = 0 means that x is non-buoyant). Hence, the resulting DEGREES MODEL (and its associated graph) will look just the same as MULTI-TRACK MODEL, but the disposition variable is interpreted differently.
DEGREES MODEL. ({BU(x),L(x),RI(x)},{RI(x) ⇐ c × BU(x) × L(x)}).
Unlike the preceding problems, dispositional degrees of (for example) buoyancy do not represent a counterexample to SCA4BUOY per se. SCA4BUOY was designed to analyse being buoyant, not having some or other degree of buoyancy. Nevertheless, some have reasonably suggested that comparisons of dispositional degrees are something we should expect a worthy analysis of dispositions to do, and for this task, any instance of SCA is clearly insufficient (Aimar 2019; Manley & Wasserman 2007; Vetter 2015).
SSEA, by contrast, does have the facility to analyse varying dispositional degrees. This is because the analysis schema accommodates any assignment of values within the range of a (potentially continuous) disposition variable. Typically, this assignment will then be reflected in the choice of function in the structural equation of the analysans. For instance, the SSEA appropriate to degrees of buoyancy might be something like the following (where k = b × c).
SSEA4BUOY (MT-DEG). For all x, BU(x) = b if and only if RI(x) ⇐ k × L(x).
I say ‘something like’, since the correspondence between changes in degree of buoyancy and change in the functional relationship between manifestation and stimulus variables may not in fact be linear (with an increase in the degree of buoyancy b having a proportional increase k = b × c in the rate of change of speeds of rising for any increase in the liquid’s density). Of course, to endorse SSEA is not to be committed to the relationship being linear, and any complexity in the influence of the degree of the disposition on manifestation can be accommodated within the relevant function over the stimulus variable(s), so long as there is an appropriate causal model. However, I do assume that to endorse SSEA as an analysis schema is at least to endorse the idea that dispositional degrees have some systematic influence on the function that relates manifestation and stimulus variables.
3.4 Summary
On the face of it, then, SSEA provides the means to analyse dispositions in a way which exhibits a number of important features. In these respects it fares better than SCA. However, it also fails to address further problem cases facing SCA, including the problem of masks, alters and mimickers. Moreover, I briefly mentioned (in §3.1) that an additional problem of ‘alternative causes’ appears to be introduced due SSEA’s requirement that manifestation counterfactually depends on stimulus. I will address all of these problem cases in §5 and §7 by introducing two further modifications to SSEA. Before that, however, it is worth pausing to address a more immediate concern.
4. Too Many Counterfactuals?
As I mentioned earlier, SCA is often treated as a template from which to develop further, more refined analyses of dispositions. Nevertheless, almost invariably, there remains only one counterfactual in the analysans. SSEA bucks this trend dramatically. As we have seen, when there is a single dichotomous stimulus variable, SSEA analyses dispositions in terms of a structural equation that encodes two counterfactuals (e.g., POSITIVE and NEGATIVE). And when the stimulus variable is continuous, there will be an infinity of counterfactuals encoded in the analysans. This might seem to be a problem, since Vetter (especially 2013; but see also 2012; 2015) has complained that, whether or not one’s hopes are for a reductive analysis of dispositions to categorical (non-modally implicating) properties, an infinity of counterfactual conditionals is a mark of undesirable complexity. This motivates Vetter to pursue a simpler approach to analysis which doesn’t employ counterfactuals at all.
Does an infinity of counterfactuals (or even a mere multiplicity) of counterfactuals in the analysans justify abandoning the structural equations approach? Not necessarily. The complexity of some analysans is arguably only a serious problem if the corresponding concepts which feature in the analysandum aren’t themselves complex. Now, it would, no doubt, be hard to justify employing a conjunction of counterfactual conditionals bearing few conceptual connections to each other in order to analyse what otherwise appears to be a simple dispositional property like buoyancy—how could such a disparate array of counterfactuals be part of the analysis of something so easy to understand as buoyancy? But SSEA isn’t guilty in this way. Indeed, the very fact that the infinity of relevant conditionals can be captured so concisely by a single structural equation tells us that the conditionals are closely conceptually related.
Perhaps it will still be objected that it is implausible that the technical notion of a structural equation underlies our conceptual understanding of dispositions as mundane as buoyancy. I’ve no doubt there aren’t structural equations present to the mind of most people thinking about such a disposition. However, it’s important to recall that our goal is not to provide a conceptual analysis of dispositional terms, but to provide an analysis of dispositions themselves (see §1). This, I suggested, is achieved when we say something informative about the necessary and sufficient conditions (potentially the grounds) for the exemplification of a disposition, where dispositions need be understood only as predicatory properties. Nevertheless, Vetter’s complaint with the complexity of multiple counterfactuals in the analysans of dispositions might seem to have renewed force by the focus on ontology. The problem is that SSEA and its modifications would seem to require that there be distinct truth-makers for each of the infinity of relevant counterfactuals for any instance of a multi-track disposition. Dispositional properties (or their associated ascriptions) then become grounded in something seemingly unwieldy—’a beast of many heads’ (Vetter 2013: 346)—inviting the question of how those truth-makers all come to be present whenever any other one is (cf. Vetter 2015: 57–58).
There are a number of assumptions made in raising this kind of concern which warrant scrutiny. The first is that the truth-makers for the infinite counterfactuals must be an infinity of distinct determinate properties (or facts, states-of-affairs, property-instances, etc.). By contrast, Kistler (2012; 2020) argues the best explanation of the infinity of counterfactuals, or ‘single-track dispositions’, which make up a conjunctive quantitative multi-track disposition, is a single unifying powerful property, for example, those implied by a determinate electrical conductivity.
If there is a unique powerful property that is the causal basis of a set of dispositions Di, it provides a unique and unifying explanation of their manifestations Mi […] In electric fields Ei of various strengths a copper wire w manifests different dispositions to produce different current densities Ji. Electrical conductivity σ is postulated as an intrinsic property of w that contributes causally to bringing about the different Ji in different fields Ei. The existence of this common causal basis makes it possible to express the relation between the different Ei to the Ji in a single equation. (2012: 126)
So, while the complexity brought about by an infinite conjunction of counterfactuals can be one philosopher’s (Vetter’s) motivation for overthrowing the counterfactual approach—and a fortiori the structural equations approach—to analysis, it can be another’s (Kistler’s) motivation for positing some unifying explanatory metaphysics. Given the diversity of intuitions about how to react to the required multiplicity of counterfactuals implied by a disposition, it would seem premature to deny the structural equations approach on its grounds. Moreover, Kistler’s example of conductivity can seem to lend credence to the reasonableness of the latter sort of reaction.
In fact, however, Vetter’s (2013) demonstration of the complexity of counterfactual analyses that motivates her radical departure from the counterfactual-based approach to analysis doesn’t draw on analyses in those terms that employ an infinite conjunction of counterfactuals (as are encoded in, e.g., the analysans of SSEA4BUOY(MT)). Rather, it draws on analyses that seem to require an infinite disjunction of counterfactuals.8 It proceeds by observing (plausibly) that the following two conditions (or something very similar) are inevitable commitments lying behind SCA.9
For all objects x that have disposition D, if x were S, then x would be M.
For all objects x that have D, if x manifests D at t, then x is M at t and x is S at or before t.10
As Vetter demonstrates, these conditions are hard to maintain together. Take the example of buoyancy. While some buoyant things will rise when immersed in even the lowest densities of liquid, others require a greater density. Say there is some threshold value T such that for any buoyant object x it rises in a liquid of density Tx ≥ T or above if immersed in it (T could be zero for the sake of argument, but is more reasonably thought of as some value similar to the density of water). Now pick some object a which will rise if immersed in a liquid of at least Ta, where Ta is greater than (and not equal to) T. It is not true of a that it will rise in a liquid of just any density greater than T, since it will not rise when immersed in densities less than Ta. Hence the stimulus for analysis of buoyancy in general can’t be the broad condition of immersion in any liquid of density greater than or equal to T, since not every instance of such a stimulus will result in manifestation, contrary to condition (i). However, if instead we choose a stimulus of immersion in a liquid of density greater than T to analyse buoyancy, say immersion in a liquid of density equal to or greater than Ta, then when objects other than a that can rise in liquids of density lower than Ta do so (and by stipulation there could be such objects), that rising cannot count as a display of those object’s buoyancy on pain of contravening condition (ii). Yet surely something rising under even lower densities than those which can count as a legitimate stimulus for buoyancy will also be a manifestation of buoyancy (context permitting)!
Although Vetter does not describe it in such terms, this problem is one of disjunctive quantitative multi-track dispositions. A disposition, like buoyancy, can manifest in more than one way, but crucially, some of its instances will not manifest in all possible ways. Hence, if buoyancy is to be analysed in terms of counterfactuals (‘tracks’) between occurrences of stimulus and manifestation, it would seem to have to be in terms of a disjunction of multiple counterfactuals: buoyancy’s instances can rise if immersed in liquid of at least this density or at least that density or …, etc.
Since SSEA entertains only conjunctions of counterfactuals in the analysans, it cannot address this problem Vetter raises. And while Kistler’s response of a unifying powerful property is plausible in the case of conjunctive multi-track dispositions, presumably it is less so for disjunctive multi-track dispositions. Nevertheless, unlike a conjunction, a disjunction does not necessarily require unification. For instance, it is commonplace to understand determinable properties as being grounded in a disjunction of possible determinate instances (Armstrong 1978; Massin 2013), and much the same can be suggested for the disjunction for dispositional properties like buoyancy. Each buoyant object x has the determinate disposition to rise in liquids of some density Tx or above (where Tx is a value greater or equal to some contextually determined threshold T). A disposition like buoyancy can therefore be analysed in terms of a disjunction of those more determinate dispositions.11
In sum, I take it that the invoked multiplicity (at least two) of counterfactuals encoded in the analysans of instances of SSEA is not in and of itself reason to reject the schema. Conjunctions of encoded counterfactuals are not obviously problematic when they are closely conceptually (e.g., mathematically) related, as those encoded by structural equations are. And the analysis is not committed to analysing dispositions in terms of a large disjunctions of counterfactuals. There are, of course, other problems with SSEA, to which we now turn.
5. Masks, Alters and Alternative Causes
Two glaring omissions of SSEA are that it provides no solution to the problems of masks or alters (finks and reverse-cycle finks). In addition, it was suggested above that SSEA would be susceptible to a problem of ‘alternative causes’. Here I introduce each of these problem cases in turn before offering an amendment to SSEA which deals with them all simultaneously.
An appropriately stimulated object’s disposition is masked when it fails to manifest that disposition due to some kind of interference with the disposed object’s causal influence on manifestation (Johnston 1992). For instance, a buoyant object x might be tied to a weight which prevents it from rising when placed in a liquid. This kind of additional interference is easily captured by MASK MODEL, characterised by the following table, which expands on MODEL 1 by employing an additional variable and a revised structural equation incorporating the additional variable’s influence on RI(x).
| Table for MASK MODEL | |||
| Variables | Structural Equations | ||
| Symbol | Possible values | Interpretation | |
| BU(x) | 1 | x is buoyant | (Exogenous) |
| 0 | x is not buoyant | ||
| L(x) | 1 | x is placed in a liquid | (Exogenous) |
| 0 | x is not placed in a liquid | ||
| WE(x) | 1 | x is tied to a weight | (Exogenous) |
| 0 | x is not tied to a weight | ||
| RI(x) | 1 | x rises | RI(x) ⇐ BU(x) × L(x) × (1 – WE(x)) |
| 0 | x doesn’t rise | ||
MASK MODEL is captured by the following pair.
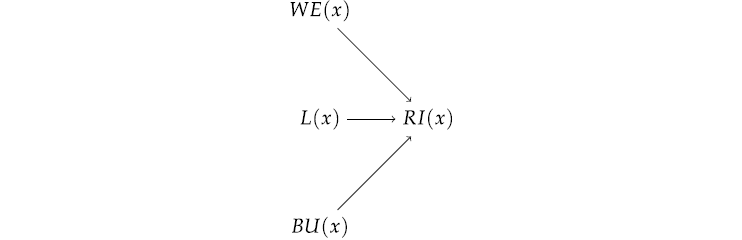
MASK MODEL. ({BU(x),L(x),WE(x),RI(x)},
{RI(x) ⇐ BU(x) × L(x) × (1 − WE(x))}).
The associated graph is displayed in Figure 3.
MASK MODEL entails certain counterfactuals which are inconsistent both with SCA4BUOY and SSEA4BUOY. In particular, it entails (assuming strong centring) that if x is buoyant (BU(x) = 1) but also tied to a weight (WE(x) = 1) then if x were immersed in a liquid (L(x) = 1) it would not rise (RI(x) = 0). Hence, the left-hand sides of SCA4BUOY’s and SSEA4BUOY’s biconditionals can be true but the right-hand side false.
Another problem for these analyses is that of altering, which is when the characteristic stimulus of a disposition influences whether or not (and to what degree) the object has that disposition. This can happen in one of two ways. One way is when an object has a disposition but is caused to lose it when stimulus occurs, as when placing a buoyant object in a liquid causes it to lose its buoyancy (e.g., through corrosion). The other way is when an object doesn’t have the disposition but is caused to gain it when stimulus occurs, as when placing a non-buoyant object in a liquid causes it to become buoyant (e.g., by causing to inflate). Charlie Martin (1994) is credited with being the first to discuss these kinds of case, for which he used the terms ‘reverse-cycle fink’ and ‘fink’, respectively. McKitrick’s (2018) more general term of ‘alter’ covers both kinds of occurrence, in the sense that the stimulus in either case alters the dispositional status of the stimulated object.
Both kinds of alter (finks and reverse-cycle finks) are easily captured in causal models containing the variables and relations of causal influence of MODEL 1, but in which BU(x) is no longer exogenous, appearing instead on the left-hand side of an additional structural equation describing a further relationship of causal influence. In the case of finks, the model would be as follows.
FINK MODEL. ({BU(x),L(x),RI(x)},
{BU(x) ⇐ L(x),RI(x) ⇐ BU(x) × L(x)}).
In the case of reverse-cycle finks, the model would be as follows.
RC FINK MODEL. ({BU(x),L(x),RI(x)},
{BU(x) ⇐ 1 − L(x),RI(x) ⇐ BU(x) × L(x)}).
Since the relationships of causal influence among variables are the same in either case, the associated graph for both models will be the same but will differ from that of MODEL 1 by an additional edge connecting L(x) to BU(x), as displayed in Figure 4.12
FINK MODEL and RC FINK MODEL entail counterfactuals that are inconsistent with SCA4BUOY and SSEA4BUOY. In particular, FINK MODEL entails that if x were placed in a liquid (L(x) = 1) it would be(come) buoyant (BU(x) = 1) and so would rise (RI(x) = 1). In the case where x is not buoyant then the right-hand sides of SCA4BUOY and SSEA4BUOY are true but the left-hand sides are false. RC FINK MODEL entails that if x were placed in a liquid (L(x) = 1) it would be(come) non-buoyant (BU(x) = 0) and so would not rise. In the case where x is buoyant, then the right-hand sides of SCA4BUOY and SSEA4BUOY are false but the left-hand sides are true.
Finally, let’s consider also the relatively new problem of alternative causes. Unlike masks and alters, this is not a problem for SCA, and arises specifically for SSEA due to the introduction of negative counterfactuals into the analysans, which were shown to help address the problem of dispositional tricks (§3.1). In fact the strategy of introducing negative counterfactuals into dispositions’ analyses has already been considered by Contessa (2016), who rejects it on the grounds that there can be cases of disposed objects in which the manifestation of a disposition can be brought about through an alternative cause to the stimulus of that disposition.
Contessa gives the example of a chameleon, Leo, who has the disposition to turn red when sitting on a ripe tomato, but will also turn red when sitting on a ripe strawberry. Leo can therefore manifest turning red through an alternative cause to the stimulus of his disposition to turn red when sitting on a ripe tomato, falsifying the inference from his having that disposition to the negative counterfactual that he would not turn red if he were not sitting on the tomato. TRICK MODEL also presents us with another case. A non-buoyant object (BU(x) = 0) being pulled up by a fishing line (FI(x) = 1) when immersed in a liquid (L(x) = 1) falsifies an inference from POSITIVE (that the object would rise when immersed in a liquid) to the buoyancy of the object. For this reason, being pulled up by a fishing line when immersed in liquid is a way to ‘trick’ us into thinking a non-buoyant object is manifesting its buoyancy. But also, being pulled up by a fishing line (FI(x) = 1) when not immersed in a liquid (L(x) = 0) falsifies the inference from the buoyancy of an object to NEGATIVE (that the object would not rise unless it were immersed in a liquid). For this reason, being pulled up by a fishing line when not immersed in a liquid is an alternative cause of the manifestation of buoyancy for a buoyant object.
How can we update SSEA to deal with both the problems of masks, alters and alternative causes? Let’s start with the observation that all three phenomena affect the functional dependency of manifestation on stimulus and disposition variables. In the case of masks and alternative causes, the functional relationship is affected by the causal influence of an additional variable on the manifestation variable (e.g., WE(x) in MASK MODEL, and FI(x) in TRICK MODEL). In the case of alters, the functional relationship is affected because the value of the disposition variable itself is influenced by the stimulus variable (e.g., L(x)’s direct influence on BU(x) in both FINK MODEL and RC FINK MODEL). In all cases, therefore, the assumption that the structural equation which accurately captures the counterfactual dependencies of the manifestation variable can be given in terms of a function only over stimulus variables with fixed value for the disposition variable (as per SSEA) must be given up. Nevertheless, we know that the stimulus variables will still feature as variables in whatever ‘true structural equation’ does relate the counterfactual dependencies of the manifestation variable. Moreover, it will remain true that were the masks, alternative causes and effects of altering not present then the functional dependencies would be captured in terms of stimulus variables only, given some fixed value of the disposition variable. In fact, we typically know something more specific: the structural equation relating only stimulus variables to the manifestation variable is a special case of the structural equation that truly captures the manifestation variable’s dependencies (where one equation A is a special case of another equation B if and only if there is an assignment of values to certain variables in B that reduces the equation to A).
Consider MASKING MODEL again. The structural equation for the manifestation variable in that model is
RI(x) ⇐ BU(x) × L(x) × (1 − WE(x)).
The equation characterises the causal influences of x’s disposition BU(x), its immersion in a liquid L(x) and whether or not x is tied down WE(x), on whether or not x rises RI(x). Notice that the special case of this equation in which BU(x) is set to 1 and WE(x) to 0 is precisely the structural equation explicit in our earlier SSEA of buoyancy, RI(x) ⇐ L(x). We can therefore explicitly state an equation relating only the stimulus variable’s causal influence on the manifestation variable which, despite not being an accurate characterisation of the dependencies actually in place, is a special case of a structural equation which does accurately characterise those dependencies.
Now consider the case of alternative causes exhibited by TRICK MODEL. The structural equation for the manifestation variable in that model is
RI(x) ⇐ BU(x) × L(x)+FI(x) − BU(x) × L(x) × FI(x).
The equation characterises the causal influences of x’s disposition BU(x), its immersion in a liquid L(x) and whether or not x is being pulled up by a fishing line FI(x), on whether or not x rises RI(x). Recall that in the case where x is buoyant but is not immersed in a liquid, since it will rise when pulled up by a fishing line, x falsifies the analysis SSEA4BUOY by contradicting the inference from right to left. Specifically, the model contradicts the inference from x’s exemplification of buoyancy to NEGATIVE, which is encoded in the analysing structural equation RI(x) ⇐ L(x). Notice, however, that this latter structural equation is, similarly to the previous case, a special case of the structural equation for the manifestation variable in TRICK MODEL (specifically, where BU(x) is set to 1 and FI(x) is set to 0). Again, therefore, we can state explicitly an equation relating only the stimulus variable’s causal influence on the manifestation variable that is a special case of an accurate structural equation for that variable.
Let’s turn, finally, to our cases of altering. In either model (FINK MODEL and RC FINK MODEL) the structural equation for whether or not x rises is
RI(x) ⇐ BU(x) × L(x).
The equation characterises the causal influence of whether or not x is buoyant BU(x) and whether or not x is immersed in a liquid L(x) on the variable for whether or not x rises RI(x). Once again, the structural equation of SSEA4BUOY is a special case of this (in which BU(x) is held fixed at 1). Again, therefore, we can explicitly state an equation relating only the stimulus variable’s causal influence on the manifestation variable which, despite not being accurate, is a special case of a structural equation which is accurate.
Obviously, the reasons the special case equations in these cases are inaccurate differ. In the masking and alternative cause case, the inaccuracy is a consequence of the possibility of the presence of the mask or alternative cause that has a direct influence on the manifestation. That means setting the disposition variable to 1 does not leave the stimulus variable as the only other causally relevant influence on manifestation. In the altering case, the inaccuracy is a consequence of the fact the stimulus can alter the disposition variable. This means that setting the disposition variable to 1 does not alone portray the actual changes that are liable to happen under certain values of the stimulus, which has a knock-on effect on the manifestation variable. But in all of these cases, it is true that the single structural equation causally relating only the stimulus to manifestation, which would feature in an SSEA for the disposition, is a special case of some more accurate equation describing all the manifestation’s actual influences. This suggests the following amendment to SSEA (no longer ‘simple’), which addresses both masks, alters and alternative causes.
SEA. For all x, D(x) = d if and only if M(x) ⇐ f(S1 (x), …, Sn(x)) is a special case of a true structural equation M(x) ⇐ …
This has the following specific instance for the disposition of buoyancy.
SEA4BUOY. For all x, BU(x) = 1 if and only if RI(x) ⇐ L(x) is a special case of a true structural equation RI(x) ⇐ …
This concludes the modification to SSEA in order to accommodate masks, alters and alternative causes. It can readily be seen that SEA4BUOY is not falsified in any of the possible variable assignments of MASK MODEL, TRICK MODEL, FINK MODEL or RC FINK MODEL. Nevertheless, a foreseeable worry one might have with the modification is that the failure of instances of SEA to specify the exact behaviour of the disposed object trivialises the analysis. I’ll address this head on in the next section.
6. Lack of Informativeness?
The task of identifying a plausible analysis that accommodates masks, alters and alternative causes is to chart a course between, on the one hand, being unreasonably specific about every possible circumstance in which a stimulus (or failure of stimulus) can fail to lead to manifestation (or failure to manifest) and, on the other hand, succumbing to triviality.13 An analysis will, after all, be trivial if it does no more than simply state that a disposition will manifest M when subject to S ‘unless it doesn’t’. And the structural equations approach I have adopted, which abandons talk of relationships between mere qualitative properties M and S in favour of functional relationships between manifestation and stimulus variables, would be liable to incur analogous triviality if it amounted to no more than the claim that this functional relationship holds ‘unless it doesn’t’.
I think it’s clear that SEA avoids this kind of triviality. SEA gives the specific reason why the manifestation variable of its instances may not be predicted by the explicit function (the special case) in the analysans: that there may be other potential causes. In this respect, SEA avoids triviality in a similar way to strategies that condition manifestation on an absence of additional causal interferences. Plenty of these latter ‘so-long-as’ strategies have been proposed in the past. For example, some analyses predict manifestation only when the disposed object is stimulated ‘ceteris paribus’, or in ‘ideal’ circumstances (Bird 1998; Kistler 2020; Mumford 1998; Steinberg 2010), others predict manifestation only when the disposed object is stimulated ‘in isolation’ (Hüttemann 2004) or when there is an absence of masks and alters (Bird 2007). By saying, for example, what kinds of reason in general prevent a disposition from manifesting in response to a stimulus, these accounts provide information about what would need to be done to achieve more predictable behaviour.
Having said all that, a limitation of all these kinds of analyses (including SEA) is that they can’t be used to say of any situation that is not fully specified what a disposed object will exactly do, since if a situation isn’t fully specified we can’t know what further causal influences might be relevant. Is that a problem? Not per se. It seems to be exactly right that an analysis for any disposition which can be subject to unknown masks, alters or alternative causes should not say what behaviour to expect of an object unless we have a total specification of the context in which it appears. Even so, there remain good reasons to think that analyses which condition predicted behaviour on an absence of recalcitrant causal influence, like the so-long-as strategies do, are not suitably informative.
One reason so-long-as strategies are not suitably informative is that there is surely a sense in which a disposed object often still exercises a disposition when stimulated despite being subject to masks, alters or alternative causes (cf. Cartwright 2009; 2019; Corry 2009; Molnar 2003). A buoyant object may not rise in the liquid it is immersed in if it is tied down, but it will exert an upward force generating tension in the tie that may lead to wear or stretching. Likewise, a buoyant object that loses its buoyancy through corrosion and subsequent deflation may rise for some period of time at an ever slower rate until its buoyancy is completely lost. Likewise, a buoyant object which is immersed in a liquid and pulled up by a fishing line may rise faster than if it were not immersed in the liquid.
The same reasoning goes for other dispositions too. For example, a wire fitted with a fuse will still conduct under contact with some high resistance conductors, even if the fuse acts as a reverse-cycle fink with lower resistances; a person who has taken an antidote subsequently to taking the poison may not come to as much harm as they would have done (the symptoms of the poison will be masked to some degree), but the amount of poison taken can still influence the degree of harm they come to; Leo the chameleon may turn red even when not sitting on a ripe tomato if he’s already sitting on a ripe strawberry, but if he’s proximal to both a ripe strawberry and a ripe tomato, his shade of red my be brighter or fuller. Crucially, all these more nuanced behaviours seem attributable to the fact that the object in question has the relevant disposition (respectively, being buoyant, being live, being poisonous, having the disposition to turn red when sitting on a ripe tomato), rather than any other distinct property. Hence, if we want to capture in our analysis everything there is to say about dispositional behaviour we will have to say something more general than just how the disposed object behaves in the select cases where masks and the like are not present.
A second reason so-long-as strategies seem insufficiently informative is that, for many dispositions (especially the capacities that appear in the characterising equations of quantitative science) masking and altering phenomena are the norm rather than the exception. Almost invariably, the heat capacity of a material is masked or altered by impurities, the carrying capacity of an environment is masked by predation, the price elasticity of a commodity is masked by policy intervention, and so on. This tells us that, insofar as we are able to empirically observe the behaviour of disposed objects under stimulation, it is typically when they are being masked (or otherwise altered or undergoing the influence of additional alternative causes) to some degree. Indeed, it is reasonable to think that some dispositions cannot be observed except in situations when they are subject to this kind of additional causal interference, such as the disposition of stiffness captured by the Hookean relationship,
load force = stiffness × extension.
Since it is a nomological impossibility that a material has no dampening effects whatsoever, this (implicitly instantaneous) relationship is never exactly revealed. The invariability of masking in so many cases of dispositional properties suggests that, even if our favoured analysis works by making reference to what the behaviour would be under stimulus if there were no other causal influences, it will have to make clear how that rare, unmasked, unaltered, causally isolated behaviour is inferentially connected to the behaviour we actually observe.
By comparison with so-long-as strategies, SEA informs us of both the above-mentioned features of dispositions. First, SEA makes it clear that stimulus variables remain a causal influence of manifestation even when other causal influences are at play. It does this by claiming that the stimulus-manifestation relationship revealed in the structural equation explicit in the analysis is always a special case of whatever true structural equation describes the influences on manifestation behaviour. SEA therefore reveals how the disposed object can still be understood to exercise its disposition in the presence of masks, alters and alternative causes. Indeed, the analysis shows how the stimulus variables remain a causal influence by specifying explicitly a function relating stimulus variables to the manifestation variable as a special case of whatever function accurately captures all the causal interactions going on. It is for this reason that an SEA for buoyancy, which offers RI(x) ⇐ L(x) as a special case of the true structural equation for any buoyant object, can explain why a buoyant object that is tied down may still create tension in the tie, since L(x) will still have a positive influence on RI(x) via the route indicated by the special case equation.14 For the same reason, the analysis can explain why a buoyant object that is being corroded may rise for some period of time or at a slower than expected rate. In any of these cases the true structural equation would incorporate other influences that prevent RI(x) taking the positive value we would expect given only the value of L(x). However, since we know that RI(x) ⇐ L(x) is a special case of the true structural equation, we can expect there to be signs that L(x) is still having some influence. (I leave it to the reader to see how analogous remarks can be made for the other cases mentioned above.)
Second, SEA suggests how we can gain empirical access to dispositions which are always or very often masked, altered or subject to alternative causes. SEA achieves this because it makes a claim exactly about disposed objects’ behaviour in cases where masks, alters and alternative causes may indeed be present. Admittedly, the analysis doesn’t say precisely what behaviour is to be expected. But, as already remarked on, we rarely have any such knowledge anyway. Crucially, what instances of SEA do tell us, which seems entirely consistent with scientific practice, is what some of the key causal relationships involved when a disposition is instantiated will be. This means that if we can hold other influences fixed, or else we can predict their probability distribution across a suitable sample of cases, an SEA analysis will tell us that we can employ known interventionist and observational strategies for testing for the presence of a disposition regardless of whether or not masks, alters or alternative causes are present.
7. Mimickers
There is at least one further, well-known problem case that has yet to be addressed within the structural equations approach being developed here: the problem of mimickers. A disposition is mimicked when circumstances are such that objects which do not have a disposition (and continue not to have it) behave as though they did because of the way they react to the imitated disposition’s stimulus (Lewis 1997). For example, a non-buoyant object can mimic being buoyant if an exothermic chemical reaction between the object’s underside and the liquid in which it’s placed accelerates the object upwards. We can capture this in MIMIC MODEL, detailed in the following table.
| Table for MIMIC MODEL | |||
| Variables | Structural Equations | ||
| Symbol | Possible values | Interpretation | |
| BU(x) | 1 | x is buoyant | (Exogenous) |
| 0 | x is not buoyant | ||
| L(x) | 1 | x is placed in a liquid | (Exogenous) |
| 0 | x is not placed in a liquid | ||
| RE(x) | 1 | x reacts with a liquid | RE(x) ⇐ L(x) |
| 0 | x does not react with a liquid | ||
| RI(x) | 1 | x rises | RI(x) ⇐ (BU(x) × L(x) + RE(x) – BU(x) × RE(x)) × L(x) |
| 0 | x doesn’t rise | ||
MIMIC MODEL is captured by the following pair.
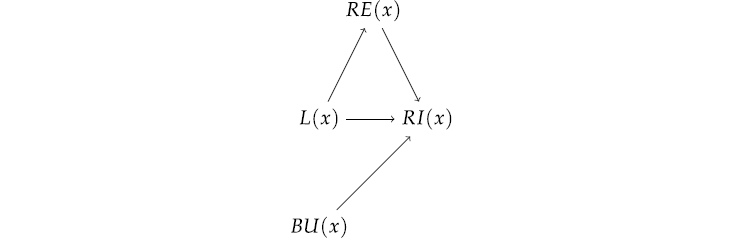
MIMIC MODEL. ({BU(x),L(x),RE(x),RI(x)},
{RE(x) ⇐ L(x),
RI(x) ⇐ (BU(x) × L(x) + RE(x) − BU(x) × RE(x)) × L(x)}).
The associated graph is displayed in Figure 5.
MIMIC MODEL entails counterfactuals which are inconsistent with SCA4BUOY and SSEA4BUOY. In particular, it entails that even if x were not buoyant (BU(x) = 0), if it were to react with a liquid in which it is immersed (RE(x) = 1), and were immersed in a liquid (L(x) = 1), it would still rise (RI(x) = 1). Hence, the right-hand sides of the biconditionals in SCA4BUOY and SSEA4BUOY can be true when the left-hand sides are false.
Arguably, not all dispositions can be mimicked. Some ‘canonical’ dispositions denoted with expressions of the form ‘the disposition to M when S’ seem to be satisfied by an object so long as the M-ing is caused by the S-ing somehow or other.15 Consider, for example, the example of the Styrofoam plate which is torn up by the hater of Styrofoam when they hear it being struck. Choi (2005) argues that such a plate has the canonical disposition to break when struck just as much as any fragile object does. Nevertheless, he admits that the Styrofoam plate doesn’t have the ‘conventional’ disposition of fragility. As Lewis puts things, ‘there is a certain direct and standard process whereby fragile things most often (actually, nowadays, and hereabouts) break when struck, and the Styrofoam dishes in the story are not at all disposed to undergo the process’ (1997: 145).
In general, the manifestations of conventional dispositions are ‘process-specific’ (Molnar 2003: 91), whereas canonical disposition perhaps need not be. In the case in which an object rises in a liquid due to an exothermic reaction, we may grant that it is disposed to rise in the liquid, but deny that it is for that reason buoyant. Like fragility, the conventional disposition of buoyancy seems to be process-specific, its manifestation involving a process which connects immersion in a liquid with rising in a different way to that enabled by a chemical reaction.
The outcome of these observations is twofold. First, we arguably need only find a way to accommodate mimickers for conventional dispositions. Second, we can’t hope to address the problem of mimickers by relying on mere counterfactual dependencies revealed in causal models. Such dependencies are relationships between sequences of events (value-instances of variables) whereas the observation of process-specificity entails that ‘the exercise of a [conventional] disposition cannot be defined as a specific kind of concatenation of events’ (Hyman 2014: 94). What we need to do, then, is incorporate into our analysis of (conventional) dispositions some or other reference to the particular process involved in a genuine exercise of the disposition.
This idea was already present in Ellis’s writing twenty years ago.
In the simplest kind of case, a dispositional property is one that is linked essentially and directly to a certain natural kind of causal process, viz., that kind of process which is a display of this property. Of course, a causal process which is superficially like those of a given natural kind might be faked, or be due to some combination of other dispositional properties. So a genuine dispositional property cannot be defined behaviouristically. Nevertheless, like natural kinds of objects natural kinds of processes may be designated. (2000: 332)
Here Ellis uses the technical notion of a ‘natural kind’ not necessarily to imply that the process must originate in nature, but to identify the processes which connect stimulus and manifestation properties in genuine exercises/displays of the disposition as something whose nature is a matter of empirical investigation rather than determined by knowledge ‘in the head’.16 My suggestion, then, is that we add to the schematic analysis developed so far a clause that the explicit structural equation linking the disposition and stimulus variables to the manifestation variable, be a special case of the true structural equation in the scenario as a consequence of the presence of (more briefly: ‘due to’) some demonstrable process that can be designated in paradigm cases of the disposition’s manifestation.17
SEA*. For all x, D(x) = d if and only if M(x) ⇐ f(S1(x), …, Sn(x)) is a special case of a true structural equation M(x) ⇐ … due to process .
The reference to something beyond the behaviouristic characterisation given by the structural equations might seem out of keeping with the general structural equations approach I’ve been developing. But this would not be a totally fair summary, as revealed by the discussion of causal modelling by Judea Pearl. No one has done more than Pearl at bringing structural equations modelling techniques to bear on questions of causation in the philosophical context. Yet his view is ultimately that ‘causal relationships are ontological, describing objective physical constraints in our world, whereas [e.g.] probabilistic relationships are epistemic, reflecting what we know or believe about the world’ (2009: 25). This understanding corresponds with how Pearl interprets the meaning of structural equations. He claims that ‘each equation represents an autonomous mechanism’ (2009: 25), where these mechanisms are irreducible features of the world, rather than entities to be further reduced to structural equations models.18
Pearl refrains from offering any account of mechanisms. However, in contemporary philosophical parlance, a mechanism is understood to comprise entities and activities organized in such a way that they are responsible for a phenomenon (Illari & Williamson 2012). Interpreting Pearl’s remarks in this way therefore puts him in agreement with Glennan (2017: 165), who claims that ‘mechanisms provide the ontological grounding that allows causes to make a difference’. When considering specifically the behavioural connection between the manifestation and stimuli associated with a disposition, the mechanism will comprise the disposed object and whatever other objects involved in the stimulation of the disposed object being appropriately arranged and engaged in that stimulating activity responsible for manifestation.
Now, in SEA* I have opted to refer to what is responsible for the behavioural connection between disposition, stimulus and manifestation variables in the same terms as Ellis, as a process. However I think the preceding understanding of mechanism would serve just as well. No doubt, metaphysicians will want to split hairs over the differences between the two, but so long as we capture with either the idea that the genuine manifestation of a disposition is a behavioural relationship between stimulus and manifestation properties due (in part) to some ontologically real and demonstrable connection, then the issue of mimickers can be dealt with by both.
Having said that, it is important (as one anonymous reviewer observed) to clarify the specificity of the notion of process or mechanism being employed here. As it is stated in SEA*, is a single kind of process. But it seems plausible that some dispositions will have manifestation behaviour which is multiply realisable. For example, all fragile objects break under applied stress, but the underlying process will be different depending on whether the fragile object is formed of covalent or ionic bonds among its constituent atoms. Analogously, an ingested poison can affect someone’s health by numerous underlying physiological processes. This raises a question over whether we should revise the analysis to allow for a plurality of possible processes to ground the dispositional behaviour, or instead should allow all the permissible processes to count as instances of .
My preference is for the latter option, leaving no change to the above schema. I will not here attempt to say exactly how the constraints on what counts as an instance of for any disposition are established. But it suffices to observe that there are constraints and, crucially, that they entail the way in which additional causal influences may be involved. For instance, we know that the process relevant to the manifestation of fragility has something to do with the direct influence of an applied stress on overcoming the energy of the intrinsic bonds (whether ionic, covalent, or whatever) between the constituents of the fragile object. And we know that the process relevant to the manifestation of poisonousness has something to do with the direct interaction between the biology of the organism that ingests it and the poison itself. Where do the constraints come from? Some appear to be conceptual. For instance, we seem to know simply by virtue of mastery of the concept that buoyancy is not exhibited when the upward thrust of an object is a consequence only of a chemical reaction. Rather, the upwards thrust must have something to do with the force exerted on the buoyant object by the liquid the object is immersed in. But some constraints on realisibility seem empirically discovered. For instance, it is presumably not part of the concept of buoyancy that the force exerted by the liquid should be a consequence of gravitational force.
The constraints on what counts as an instance of the underlying process for a disposition will add limitations to whichever true structural equation describes the counterfactual dependencies experienced by an object disposed in that way. They cannot stipulate against external influences, of course, since that would preclude the potential influence of unknown alters and masks, which I have argued a good analysis ought to accommodate. Rather, the constraints place a limit on how additional variables are involved. For instance, it may be that some instance of buoyancy is affected by the chemical reaction between itself and the liquid in which it’s immersed. Consequently, the true structural equation for how that object rises will include variables for reactivity. However, the process by virtue of which the equation definitive of buoyancy is a special case of that true structural equation will not itself be one that underlies the influence of chemical reactivity. Rather, the true structural equation will accurately represent the scenario due to the presence of at least two processes: one that underlies the behaviour definitive of buoyancy, the other that underlies the influence of the chemical reaction. Such a difference is one we can expect to be revealed under ‘natural’ expressions of the true structural equation (were we able to make it explicit), for example, by the manifestation variable of rising being written as a function of two terms, one representing the influence of the water pressure, the other the influence of the chemical reaction.19
SEA* marks the final analysis to be proposed in the present discussion. By inheriting the benefits of SEA, which inherited the benefits of SSEA, which itself inherited the benefits of SCA, this final analysis has the means to respond to a host of problem cases. Indeed, I’m unaware of any other analysis which has quite this range of success.20 At the very least, I hope to have now shown that mimickers do not pose a problem.
8. Conclusion
My aim in the preceding discussion has been to reveal the utility of bringing the structural equations modelling framework to bear on the analysis of dispositional properties. Specifically, I hope to have shown how structural equations can be employed in a novel analysis schema for dispositional properties (SEA*) which avoids many of the problem cases raised in discussion of analysis of dispositions. In the process I also hope to have shown how the framework can be usefully employed to make salient the different issues revealed by well-known problem cases for analysis. Even if one does not ultimately accept the structural equations approach to analysis I have proposed, the utility of structural equations modelling to making sense of and problematising analyses of dispositions should be clear. One crucial example of this is the demonstration in terms of causal models of the similarity between cases of masking, dispositional tricks and alternative causes (§5). But the utility has also been highlighted by the demonstration that both scenarios of altering (finks and reverse-cycle finks) have the same causal structure.
In advocating for a structural equations approach to analysis I made reference mostly to the simple counterfactual analysis (SCA) as the central foil. However, there are many extant analyses which fare better than SCA, such as those which analyse dispositions in terms of generics (see Wasserman 2011 for a survey), proportionality (Manley & Wasserman 2007; 2008, Wasserman 2011) or possibility (Aimar 2019; Vetter 2014; 2015). Readers with an interest in these other accounts will have to assess for themselves whether they think SEA* remains competitive when compared with them. I, for one, can think of no other account besides SEA* which so roundly deals with all of the problem cases discussed above.
Those immersed in the debate will also know that I have failed to address all the problem cases which beset SCA, some of which remain problems for SEA* too. For example, SEA* does not avoid the problem of ‘minkish dispositions’ (Hájek 2020) which are such that they might not manifest when subject to stimulus, such as when the causal connection between stimulus and manifestation is probabilistic. Yet I do not see why SEA* (or, indeed, SCA) might not be adapted to handle such dispositions by simply replacing the manifestation variable with a variable whose values are probability distributions over the manifestation variable.
SEA* also fails to address dispositions that appear to have no stimulus conditions at all (Aimar 2019; Fara 2005; Hájek 2020; Manley & Wasserman 2008; Vetter 2015). For example, a disposition like radioactivity should arguably be analysed in terms of the possibility that an object radioactively decays rather than in terms of it decaying under some or other antecedent causal condition. Since SEA* (like SCA) requires that specific stimulus properties get named in the analysans, it can’t handle these kinds of case. Nevertheless, I don’t think this should pressure us to abandon the structural equations approach to analysis. And a solution to this issue might be found by adapting SEA* to permit no specification of stimuli whatsoever, for example, by allowing a constant to replace the function over stimulus variables in the explicit structural equation.
Yet a further problem case (not often distinguished from the previous) is when a disposition requires stimulating in order to manifest, but doesn’t require any specific stimulus. For example, breakability should arguably be analysed in terms of the fact that some influence or other can cause it to break, where it doesn’t matter what that influence is. Counterfactual analyses in general can be adapted to accommodate this sort of disposition by quantifying over stimuli: there is some stimulus such that were it to occur, the manifestation would occur. In the case of the structural equations approach, this suggestion would end up as a quantification over stimulus functions: there is some function over certain stimulus variables such that the explicit structural equation relating that function to the manifestation variable is a special case of a true structural equation for the manifestation variable due to process .
Obviously, the preceding remarks on how to deal with remaining problems for SEA* have been brief. But I hope they are sufficient to prevent its swift rejection.
Notes
- Technically, the debate has been around developing a schema for analysis rather than specific analyses themselves, which should correspond to ‘instances’ of the schema. However, I’ll often pass over this nuance and talk as though the schema itself is an analysis. ⮭
- In the causation literature, explicit reference to instantiating particulars is not commonplace. I make it explicit here in order to more easily incorporate structural equations within an analysis of dispositions later on. ⮭
- I do not claim that stimuli are ontologically any different from dispositions themselves. If one prefers they may be coherently called ‘manifestation partners’ instead (as per Heil 2010; Martin 2008; Mumford & Anjum 2011). ⮭
- For example, SCA is used in this way by Bird (2007), Choi (2008), Contessa (2013; 2016), Fara (2005), Lewis (1997), Manley and Wasserman (2007), Vetter (2015). ⮭
- While it is often the case that there is only one relevant stimulus variable, and that the stimulus variable property is a property of the disposed object (i.e., x = y1 = … = yn), this needn’t be the case, although I will mostly ignore this fact in what follows. ⮭
- Not to be confused with disjunctive multi-track dispositions, whose instances must satisfy one or other of some collection of stimulus-manifestation relations (see §4 for more discussion). ⮭
- Barberousse (2007) appears to suggest that temperature change is a stimulus and heat absorption the manifestation of specific heat capacity. I agree with McKitrick (2008) that this has the causal order of the variables muddled. ⮭
- In Vetter’s (2015) book she considers both kinds of analysis but does not clearly distinguish them (compare the argument for the multi-track nature of fragility, pp. 43–50, with the argument for the multi-track nature of electric charge, pp. 50–53). My claim is that the distinction is important, since each warrants a different response. ⮭
- Unlike (i), instances of (ii) are not entailed by their corresponding analyses of SCA form. Nevertheless, this condition is a natural presupposition. If a disposition could count as manifesting by exhibiting some other manifestation than M, or by exhibiting M in some other way than in response to S, then an analysis of the disposition should surely take that into account. ⮭
- I leave Vetter’s ceteris paribus clause out for simplicity. ⮭
- In fact, Vetter entertained such a solution (see the discussion of ‘C8’ in her 2015: 48–49) complaining that it fails to collapse the analysis down to a single conditional. Of course, our aim here has not been to advocate for SCA but to propose something better. Vetter also complained more generally that a determinate-determinables strategy for dealing with multi-track dispositions is unavailable because the exemplification of a determinate property typically excludes co-exemplification of any other determinate under the same determinable (2013: 346; 2015: 53; see also 2012: 125). While this precludes the use of this strategy for dealing with conjunctive multi-track dispositions it does not preclude it for dealing with disjunctive multi-track dispositions. A buoyant object, for example, has only one determinate value (to the exclusion of others) for the density of a liquid above which it will rise if immersed in it. ⮭
- An anonymous reviewer asked how either model could provide an explication of BU(x) when it renders the manifestation variable RI(x) entirely dependent on the stimulus variable L(x). Clearly these models alone can’t for this reason be sufficient to capture the nature of BU(x). But that is not something we should have expected anyway, given that altering is only one kind of interference dispositions can undergo. Nor does the model trivialise the nature of buoyancy. For example, if the relationships were non-deterministic or more quantitatively complex, then it would no longer be inevitable that the manifestation variable could be expressed merely in terms of the value of the stimulus variable. ⮭
- Dealing with masks and alters by being specific about every possible circumstance has been rightfully objected to on the grounds that whatever qualification could go into the analysis would have to be enormously complex if not open-ended (see also Mumford 1998: 88). It is surely implausible that dispositions have such complex analysans. Given the ease with which we conceptually grasp dispositional terms like ‘is buoyant’ it cannot be that we learn anything so complex. ⮭
- Of course, some peculiar alter could make the net effect of the object’s buoyancy have a negative influence. But I don’t take this possibility to undermine an explanation of a positive influence when there is one. ⮭
- Choi (2008) argues that canonical dispositions are not subject to masks or finks either, see also Hájek (2020). ⮭
- Ellis also takes the dispositional properties to explain the processes which are displays of them. This would be to go beyond the interpretation employed here of dispositional properties as merely predicatory, i.e., something acceptable to categoricalists and powers theorists alike. ⮭
- The fact that the explicit structural equation’s status as a special case of the true structural equation is a consequence of the underlying process might reasonably be interpreted in terms of the existence of the process making this fact true. Although I do not see any reason beyond the usual considerations why the analysis is particularly committed to truth-maker theory. ⮭
- Admittedly, not everyone believes that the order of explanation is this way round; see Woodward (2003; 2004). ⮭
- It is another question what makes one expression of an equation more natural than another. I leave exploration of this thorny issue to another occasion. ⮭
- Compare, e.g., the comprehensive survey of analysis strategies and their corresponding failures in Friend and Kimpton-Nye (2023: ch. 2). ⮭
Acknowledgments
I’m grateful to Samuel Kimpton-Nye and Max Kistler, who gave me significant feedback on my section in Sam’s and my book Dispositions and Powers (Friend & Kimpton-Nye 2023) which formed the basis of this article. The research for this article has received funding from the European Research Council (ERC) under the European Union’s (EU) Horizon 2020 research and innovation programme, grant agreement No 771509 (‘MetaScience’).
References
Aimar, S. (2019). Dispositional Ascriptions. Philosophical Studies, 176(7), 1667–92.
Armstrong, D. (1978). A Theory of Universals. Cambridge University Press.
Barberousse, A. (2007). Are Specific Heats Dispositions? In M. Kistler and B. Gnassounou (Eds.), Dispositions and Causal Powers (271–82). Ashgate.
Bird, A. (1998). Dispositions and Antidotes. The Philosophical Quarterly, 48(191), 227–34.
Bird, A. (2007). Nature’s Metaphysics: Laws and Properties. Clarendon Press.
Bird, A. (2010). Causation as the Manifestation of Powers. In A. Marmodoro (Ed.), The Metaphysics of Powers: their Grounding and their Manifestations (160–168). Reidel.
Bird, A. (2016). Overpowering: How the Powers Ontology Has Overreached Itself. Mind, 125(498), 341–83.
Bird, A. (2018). Fundamental Powers, Evolved Powers, and Mental Powers. Aristotelian Society Supplementary Volume, 92(1), 247–75.
Carnap, R. (1936). Testability and Meaning. Philosophy of Science, 3(4), 419–71; 1–40.
Cartwright, N. (1989). Nature’s Capacities and Their Measurement. Oxford University Press.
Cartwright, N. (1999). The Dappled World: A Study of the Boundaries of Science. Cambridge University Press.
Cartwright, N. (2009). Causal Laws, Policy Predictions, and the Need for Genuine Powers. In T. Handfield (Ed.), Dispositions and Causes (3–60). Clarendon Press.
Cartwright, N. (2019). Nature, the Artful Modeler. Open Court Publishing.
Choi, S. (2005). Dispositions and Mimickers. Philosophical Studies, 122(2), 183–88.
Choi, S. (2008). Dipositional Properties and Counterfactual Conditionals. Mind, 117(468), 795–841.
Contessa, G. (2013). Dispositions and Interferences. Philosophical Studies, 165(2), 401–19.
Contessa, G. (2016). Dispositions and Tricks. Erkenntnis, 81(3), 587–96.
Corry, R. (2009). How Is Scientific Analysis Possible? In T. Handfield (Ed.), Dispositions and Causes (158–88). Clarendon Press.
Ellis, B. (2000). Causal Laws and Singular Causation. Philosophy and Phenomenological Research, 16(2), 329–51.
Fara, M. (2005). Dispositions and Habituals. Noûs, 39(1), 43–82.
Friend, T. and S. Kimpton-Nye (2023). Dispositions and Powers. T. Tahko (Ed.). Elements in Metaphysics. Cambridge University Press.
Glennan, S. (2017). The New Mechanical Philosophy. Oxford University Press.
Hájek, A. (2020). Minkish Dispositions. Synthese, 197(11), 4795–811.
Halpern, J. and J. Pearl (2001). Causes and Explanations: A Structural-Model Approach—Part I: Causes. Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence (194–202).
Heil, J. (2010). Powerful Qualities. In A. Marmodoro (Ed.), The Metaphysics of Powers: Their Grounding and Their Manifestations (58–72). Routledge.
Hitchcock, C. (2001a). A Tale of Two Effects. Philosophical Review, 110(3), 361–96.
Hitchcock, C. (2001b). The Intransitivity of Causation Revealed in Equations and Graphs. Journal of Philosophy, 98(6), 273–99.
Hüttemann, A. (2004). What’s Wrong with Microphysicalism? Routledge.
Hyman, J. (2014). Desires, Dispositions and Deviant Causal Chains. Philosophy, 89(1), 83–112.
Illari, P. and J. Williamson (2012). What Is a Mechanism? Thinking about Mechanisms across the Sciences. European Journal for Philosophy of Science, 2(1), 119–35.
Johnston, M. (1992). How to Speak of the Colors. Philosophical Studies, 68(3), 221–63.
Kistler, M. (2012). Powerful Properties and the Causal Basis for Dispositions. In A. Bird, B. Ellis, and H. Sankey (Eds.), Properties, Powers and Structures (119–38). Routledge.
Kistler, M. (2020). Powers, Dispositions and Laws of Nature. In A. S. Meincke (Ed.), Dispositionalism: Perspectives from Metaphysics and the Philosophy of Science (171–88). Springer.
Lewis, D. (1997). Finkish Dispositions. The Philosophical Quarterly, 47(187), 143–58.
Manley, D. and R. Wasserman (2007). A Gradable Approach to Dispositions. The Philosophical Quarterly, 57(226), 68–75.
Manley, D. and R. Wasserman (2008). On Linking Dispositions and Conditionals. Mind, 117(465), 60–84.
Martin, C. B. (1994). Dispositions and Conditionals. The Philosophical Quarterly, 44(174), 1–8.
Martin, C. B. (2008). The Mind in Nature. Oxford Clarendon Press.
Massin, O. (2013). Determinables and Brute Similarities. In C. Svennerlind, J. Almäng, and R. Ingthorsson (Eds.), Johanssonian Investigations: Essays in Honour of Ingvar Johansson on His Seventieth Birthday (388–420). Ontos Verlag.
McKitrick, J. (2008). Dispositions and Causal Powers. Notre Dame Philosophical Reviews. https://ndpr.nd.edu/reviews/dispositions-and-causal-powers/
McKitrick, J. (2010). Manifestations as Effects. In A. Marmodoro (Ed.), The Metaphysics of Powers: Their Grounding and their Manifestations (73–83). Routledge.
McKitrick, J. (2018). Dispositional Pluralism. Oxford University Press.
Molnar, G. (2003). Powers: A Study in Metaphysics. Oxford University Press.
Mumford, S. (1998). Dispositions. Oxford University Press.
Mumford, S. and R. L. Anjum (2011). Getting Causes from Powers. Oxford University Press.
Pearl, J. (2009). Causality (2nd ed.). Cambridge University Press.
Ryle, G. (1949). The Concept of Mind. Penguin.
Steinberg, J. (2010). Dispositions and Subjunctives. Philosophical Studies, 148(3), 323–41.
Storer, T. (1951). On Defining ‘Soluble’. Analysis, 11(6), 134–37.
Vetter, B. (2012). Dispositional Essentialism and the Laws of Nature. In A. Bird, B. Ellis, and H. Sankey (Eds.), Properties, Powers and Structures (201–15). Routledge.
Vetter, B. (2013). Multi-Track Dispositions. The Philosophical Quarterly, 63(251), 330–52.
Vetter, B. (2014). Dispositions without Conditionals. Mind, 489(489), 129–56.
Vetter, B. (2015). Potentiality: From Dispositions to Modality. Oxford University Press.
Wasserman, R. (2011). Dispositions and Generics. Philosophical Perspectives, 25(1), 425–53.
Woodward, J. (2003). Making Things Happen. Oxford University Press.
Woodward, J. (2004). Counterfactuals and Causal Explanation. International Studies in the Philosophy of Science, 18(1), 41–72.