The Logic of Contingent Actuality

1. Introducing Contingentism

Contingentism and its negation Necessitism may be stated as follows:¹

Contingentism For some $p$, actually $p$, and possibly actually not-$p$.

Necessitism For all $p$, if actually $p$ then necessarily actually $p$.

There are many notions of possibility and necessity; here we have in mind absolute, unrestricted metaphysical modality.² Let us also try to clarify the target notion of actuality somewhat. Consider the statement:

(1) The weather could have been nicer than it actually is.

On a natural reading, (1) makes a point about how the weather across various alternative possibilities compares with the actual weather we are experiencing right now, and it is very plausibly true. The notion of actuality that we target in this paper, and that yields the pertinent readings of Contingentism and Necessitism, is the notion involved in this reading of (1).³

We shall call (1) and its ilk modal comparisons. Such comparisons have been central to most discussions of actuality in the context of modal logic and in particular of its modal profile, so it seems safe to say that the relevant authors have been targeting the same notion that we have in mind.⁴ As indicated, with respect to metaphysical, absolute necessity, Necessitism has more or less invariably been accepted in these contributions (see, for example, Crossley & Humberstone 1977; Hazen 1976; and Hodes 1984a).

Our acceptance of (1) distinguishes our view from some others that might also be seen as forms of contingentism about actuality. One such view is suggested by Adams’s remark that ‘presumably the nonactual possible worlds could have been actual and are possibly actual. Each possible world is actual in some possible world—namely, in itself’ (1974: 221; see also Lewis 1970: 185–86). On this view, however nice the weather could have been, if it had been that nice, it would have actually been that nice—and so it would not have been nicer than it actually is. On this view, (1) is false.

We do not deny that there is a thin notion of actuality for which this view is correct. Actuality in this thin sense is redundant: to say that the weather is actually nice is simply to say that it is nice. But this notion is not our target here. We mean to target the notion of actuality on which (1) is true. Although we have not yet developed the details of our view, the truth of (1) makes it clear that the notion of actuality is not redundant. It does something.

A second form of contingentism about actuality is prominent in the two-dimensionalist tradition (Davies & Humberstone 1980; Chalmers 1996). These two-dimensionalists embrace a distinction between two ways of considering possible worlds: they can be considered ‘as counterfactual’ or ‘as actual’. The two ways of considering correspond to two notions of modality: truth in all worlds considered as counterfactual corresponds to one notion of necessity, truth in all worlds considered as actual to a second notion. And if we consider possible worlds as actual, the two-dimensionalists say, then many propositions of the form ‘actually $p$’ will be contingent. For there is a world in which snow is white and a world in which it is green, and if we consider each world as actual, then the first is a world in which snow is actually white, the second a world in which it is actually green.

Two major differences between this view and ours should be noted (see §8 for further discussion). First, we take contingentism to hold with respect to metaphysical modality; two-dimensionalists do not. Two-dimensionalists take contingentism to hold only with respect to the notion of modality that corresponds to considering possible worlds as actual, and that notion, they think, is not the notion of metaphysical modality. Second, if we consider possible worlds as actual (whatever exactly that comes to), then (1) will not be true. After all, if possible worlds are considered as actual, then there can be no world at which the weather is nicer than it actually is. Quite the contrary: at every world the weather must be exactly as nice as it actually is! On our view, by contrast, (1) is true.^5,6

We believe that Contingentism has a large number of verifying instances and that these are not at all recherché or isolated. For instance, we claim that although it is actually sunny today, it could have been actually rainy, and although there is actually a global pandemic, it could have been the case that there is actually no global pandemic. In this sense, we take Necessitism to be very wrong: counterexamples are widespread, and these counterexamples are not obscure cases which proponents of Necessitism have happened to overlook. They are examples in which Necessitists have simply rejected our assessment of the modal status of claims involving ‘actually’.

But how could Necessitism be so wrong? Is it not in fact presupposed by the way we use ‘actually’ in modal comparisons? And if it is, then can we really stomach the conclusion that our practice of modal comparison rests on a false presupposition?

Let’s unpack this worry a bit. Consider again the claim that the weather could have been nicer than it actually is. What is it supposed to say? Well, suppose the weather is nice to degree $n$. Then surely our modal comparison, under its intended reading, is true just in case the weather could have had a degree of niceness greater than $n$. Necessitism straightforwardly secures this result. But Contingentism, it may seem, makes room for an unintended way for the modal comparison to be true. For suppose that there is no world at which the weather is nice to some degree $m>n$. Then the modal comparison, it seems, should be false. But there might still be a world at which both of the following hold: the weather is nice to some degree , and the weather is actually nice only to some degree . Then the modal comparison comes out true after all!

We agree that this argument shows that our practice of modal comparison does presuppose a kind of necessitism. Whatever form of modality is involved in typical modal comparisons—whatever ‘could’ means in ‘the weather could have been nicer than it actually is’—necessitism must indeed hold with respect to that form of modality. We think, however, that typical modal comparisons do not involve absolute, unrestricted metaphysical modality. We therefore deny that the argument establishes Necessitism as defined in this paper.

So what form of modality do these comparisons involve? We claim they involve a restricted form of modality that we call necessity (or possibility) given actuality.⁷ For something to be necessary given actuality is for it to be necessary, holding fixed what actuality is like. Correspondingly, for something to be possible given actuality is for it to be possible, holding actuality fixed. It is easy to see that with respect to necessity given actuality, the actuality operator behaves in just the way that Necessitism says it behaves with respect to absolute, unrestricted necessity. In particular, by the definition of necessity given actuality, we have

Restricted Necessitism For all $p$, if actually $p$, then it is necessary given actuality that $p$.

As a result, when modal comparisons are interpreted as concerning necessity or possibility given actuality, then even under our view, they receive exactly the expected truth-conditions. (Note that the Necessitist will even agree with our ascription of truth-conditions to ordinary modal comparisons, since for her—though not for us—necessity given actuality simply coincides with unrestricted necessity.)

We might give the following picture of modal comparisons. By intoning ‘necessarily’ or ‘possibly’, we launch ourselves out into modal space, to other possible worlds at which things are different from the way they are here. Then in order to compare how things are at these worlds with how they in fact are, we intone ‘actually’. That incantation sends us back home. It sends us to a world such that what is true at that world perfectly matches what is, in fact, true.

Now the Necessitist thinks that ‘actually’ sends us back home no matter where we are in modal space. We disagree. We think it only sends us back home from some worlds. From other worlds, ‘actually’ sends us to a modified version of home—a world where the way things are is a way they actually could have been, but not the way they in fact are. It is just that, in modal comparisons, we typically exclude these other points in modal space from consideration.⁸

In many cases, it won’t make a difference to the modal status of a proposition whether these points are excluded or not. That is, for many propositions, it is plausible that they are possible simpliciter iff they are possible given actuality. According to Contingentism, many propositions involving the notion of actuality are exceptions in that they are possible, but not possible given actuality. But it is consistent with our view that this is the only type of exception, that is, that all propositions not involving the concept of actuality are possible given actuality iff they are possible simpliciter.

Our view, then, has two main components. The first is Contingentism. The second is the claim that modal comparisons typically involve necessity or possibility given actuality, rather than absolute, unrestricted metaphysical modality. The next section briefly gives some of our reasons for accepting these claims.

2. Motivation for Contingentism

Why would anyone accept Contingentism? Here is what we take to be the best reason.⁹ Suppose you thought that if something was the case at some point in the past, then it can’t be impossible for that thing to be the case: nothing impossible was ever true. Call this principle the Possibility of the Past. You might accept this because it seems intuitively overwhelmingly plausible, and/or because you have been convinced by an explicit philosophical defence of the principle, as offered recently by Cian Dorr and Jeremy Goodman (2020).¹⁰ Now suppose you also accept another seemingly obvious platitude, namely that actuality changes over time: it used to be different than it is now. Call this the Temporality of Actuality. You can then straightforwardly infer that it is possible for actuality to be different, and hence that Necessitism is false.¹¹

Let us consider Temporality of Actuality in a bit more detail, and look at a concrete example. To the dismay of five-year-olds everywhere, there are no longer any (living) dinosaurs. It is agreed on all sides that we may infer from this that there are actually no dinosaurs. But of course there used to be dinosaurs. We maintain that we may infer from this that there used to actually be dinosaurs. Actuality changes over time.

For the sake of precision, let’s impose a bit of regimentation on our language. We’re going to give present-tensed verbs a temporally neutral reading, as is common practice in discussions of tense logic. So a present-tensed verb, on its own, will not convey any temporal information. Such information will be conveyed only by the use of operators like ‘it used to be the case that’, not by the tense of verbs appearing outside such operators.

To understand how this works, consider the sentence ‘it is not the case that there are dinosaurs, but it used to be’. This sentence is elliptical: it used to be what? The answer is: it used to be the case that there are dinosaurs. But don’t be misled by the present tense in ‘there are dinosaurs’. What this sentence says is just that there aren’t any dinosaurs now but there were some in the past. It does not say, incoherently, that although there aren’t any dinosaurs now, at some point in the past it was true that there are dinosaurs now. In order to get the true reading of the sentence, and avoid the incoherent reading, we have to adopt a certain reading of the present tense in ‘there are dinosaurs’: the temporally neutral reading. Our regimentation imposes this neutral reading on all present-tensed verbs.

Given this regimentation, then, we can convey the erstwhile presence of dinosaurs by saying, ‘it used to be the case that there are dinosaurs’. And what we maintain is that from this we may infer that

(2) It used to be the case that, actually, there are dinosaurs.

Now one might have reason to reject (2) if one gave the present tense a temporally non-neutral reading. But we have set that reading aside. Still, it might be claimed that even under the neutral reading, (2) is false, since the presence of ‘actually’, all on its own, changes the time of evaluation back to the present. The following example of a modal comparison seems to us to show otherwise.

We begin with a warm-up case to set the stage. As a matter of fact, there are many birds in existence. But birds could have gone extinct long ago. So in particular, it is possible for there to be fewer birds than there actually are. And the same goes for dogs, squirrels, wombats, and so on. But not for dinosaurs: since there are no dinosaurs, there couldn’t be fewer dinosaurs than there actually are. Still, what holds of birds and dogs and so on surely used to hold of dinosaurs, back when there were still dinosaurs around. That is,

(3) It used to be possible for there to be fewer dinosaurs than there actually are.

Now if ‘actually’ always changed the time to the present, there should not be any true reading available for (3). But it seems clear that there is. Moreover, it seems that the relevant reading of ‘actually’ is the same reading that is involved in the simpler modal comparisons concerning birds and dogs. Otherwise it should sound peculiar to say that what we saw to hold of birds and dogs used to hold of dinosaurs, and it does not.

We conclude that ‘actually’ has a reading under which Temporality of Actuality holds. Moreover, this is precisely the reading required for certain kinds of modal comparisons: it is because ‘actually’, under the relevant reading, does not change the time to the present that it allows us to make the desired modal comparison: a comparison not of what is the case with what could have been the case, but one of what used to be the case with what, back then, could have been the case.^12,13

Having motivated Contingentism, we turn to the second component of our view. This is our claim that the form of modality involved in modal comparisons is what we have called necessity (or possibility) given actuality. Why should we accept that? Why think, that is, that in making a modal comparison like (1), we restrict attention to a special subset of the set of possible worlds, namely those in which actuality is held fixed?

Our initial answer is simple. If we did not so restrict attention, we would be saying something other than what we want to say. What we want to do is to compare the way things could have been with the way things actually are. To do that properly we need to hold fixed the way things actually are. We cannot let it wriggle around as we move from world to world. In saying (1), for example, we intend to say that there is a world at which the weather is nicer than it is here, in our modal home. If we did not exclude from consideration worlds where actuality is different, and where ‘actually’ therefore does not take us home, then as we saw above, our claim could be true for an unintended reason: because there’s a world whose weather is worse but whose actuality has worse weather still. Once one admits worlds in which actuality is otherwise than it in fact is, one has to straightaway exclude such worlds from consideration in modal comparisons in order for their truth conditions to come out right.

This answer, however, may seem in some way lacking. Granted, given that ‘actually’ does not always take us back home, modal comparisons using ‘actually’ need to exclude from consideration those worlds where it does not. But then why aren’t we making modal comparisons with the help of a different operator (or the same one under a different interpretation) which does always take us back home, and thus does not make it necessary to restrict attention to a subregion of modal space? Indeed, our very talk of ‘home’ would seem to presuppose the intelligibility of such an operator.

We agree that such an operator is intelligible, and we will continue to use ‘(at) home’ for it. The worry is that this operator would seem to be well suited for making modal comparisons—and indeed better suited than the ‘actually’ operator (as we construe it) is. Should we not therefore expect that ‘actually’, in the mouths of ordinary speakers, will pick out something closer to ‘at home’ than to our Contingentist construal of actuality?

No. Despite how things may have appeared, the ‘at home’ operator is not adequate for modal comparison. For as we have seen, we make comparisons, not only between what could have been and what is, but also between what could have been and what was. We compare, for instance, the number of dinosaurs there were with the lower number of dinosaurs there could have been. But if we try to do this using ‘at home’ we run aground. Suppose we say, on the model of (3), that it used to be possible for there to be fewer dinosaurs than there are at home. By Possibility of the Past, this entails that it is possible for there to be fewer dinosaurs than there are at home. But of course at home there are zero dinosaurs, and since by stipulation ‘at home’ is Necessitist—since it takes us back home no matter where we are in modal space—it is not possible for there to be fewer dinosaurs than there are at home. So our attempt at modal comparison misfires.

Proper modal comparison—and in particular, proper comparison of what could have been with what was—requires ditching ‘at home’ for an operator that obeys Contingentism. It is therefore worth studying the logical properties of such an operator. This operator, in our view, is the actuality operator, and this study is the topic of the remainder of this paper.

But before turning to that, let us note a further potential application of Contingentism, one not involving modal comparison. Suppose I am about to flip a ‘chancy’ coin. If the coin is genuinely chancy, then there must be a sense in which it is contingent how it will land—in which it is possible for the coin to land heads and possible for it to land tails. But there is also some temptation to say that something further is also contingent. Not only is it contingent how the coin will land, it is contingent how it will actually land. And so it is possible for the coin to actually land heads and possible for it to actually land tails. If the notion of possibility involved in this tempting thought is metaphysical possibility, and if the notion of actuality is our target notion of actuality, then the Contingentist (alone) is in a position to neatly accommodate its truth.

The tempting thought does at least seem to involve a ‘genuine’, non-epistemic form of modality. The idea is clearly to say something not just about what is left open by what we know but about what is really possible. One might quibble over whether the relevant sense of possibility is metaphysical possibility or some other genuine form of possibility, such as nomological possibility or (perhaps) historical possibility. But this question matters little, since it is plausible that these other candidate forms of possibility entail metaphysical possibility. Whatever is nomologically possible, for example, will be metaphysically possible too. And so if the tempting thought is true of some genuine form of possibility, it is also true of metaphysical possibility.

It is less clear, however, whether the tempting thought involves our target notion of actuality. For one might hold that it involves only the thin, redundant notion of actuality mentioned in §1, and we know of no decisive argument against this position. But for those who are convinced that, in our target sense of ‘actually’, it is contingent how the coin will actually land, Contingentism offers an attractive way of making sense of this claim.

3. Limits of Contingency

We may distinguish two ways of using the term ‘actuality’. On one use, it refers to a certain notion, the one expressed by ‘actually’ in ordinary modal comparisons like (1). Actuality in this sense may be formalized as an operator: given a proposition $p$, ‘actually $p$’ is also a proposition (a true one, if $p$ is true). But there is also a second use of the term ‘actuality’, on which it refers to whatever propositions happen to be actually true. For example, since the Contingentist holds that there is at least one proposition $p$ which is actually true but which could have been actually false, we may say that the Contingentist thinks that actuality could have been different. We will usually leave it to context to make clear which sense of ‘actuality’ is at issue.

Contingentism says that actuality (in the propositional sense) could have been different. But how different? Put another way: which collections of propositions are such that it is possible for them to be exactly the propositions that are actually true? Some partial answers to this question follow from what we have said so far. For instance, since all true propositions are also actually true, the collection of all the true propositions is one example. More substantially, given what we have said about tense, modality, and actuality, it is clear that every collection of propositions that was once precisely the collection of true propositions is also an example. We might describe these possible actualities as time-shifted versions of actuality.

Are all possible actualities time-shifted versions of actuality? Here is one reason to think the answer is ‘no’ (others are discussed in Glazier 2023). Consider Peter van Inwagen’s (1980; 1983) principle that no one can be responsible for a necessary truth. Although this principle has met with broad acceptance, it faces a challenge due to Stephen Kearns (2011).¹⁴ For suppose Oswald commits murder, and so actually commits murder. Then he is responsible for both the fact that he murders and the fact that he actually murders. But, Kearns argues, that Oswald actually murders is necessary. So he is responsible for a necessary truth. Van Inwagen’s principle is false.

A simple way to avoid this conclusion is to allow that, at some worlds, ‘actually’ does not take us back home and instead takes us to a world at which Oswald does not murder. That would save van Inwagen’s principle, since now ‘Oswald actually murders’ is no longer a necessary truth.

Notice, however, that Kearns’s argument can be run entirely in terms of eternal propositions: just read ‘Oswald murders’ as ‘at some time or other, Oswald murders’. To save van Inwagen’s principle, then, ‘actually’ must be capable of taking us to a world at which Oswald never murders. But such a possible actuality is not a time-shifted version of actuality.¹⁵

We do not take this example to show definitively that some possible actualities are not time-shifted versions of actuality. But we do think the issue should be left open at the present stage of inquiry. And even if you disagree, it does not matter too much for our present purposes. For our main concern here will be to determine the quantified modal logic of ‘actually’, in which there are no tense operators. So the putative constraint on the space of possible actualities does not make a difference to the logical systems that we shall study here.

But although we will not attempt to impose this constraint, there are others that we think should be laid down. There are limits to how different actuality could have been. These limits are imposed by the nature or essence of actuality (in the operational sense). Just as the nature of water requires that, necessarily, water is ${\text{H}}_{\text{2}}\text{O}$, and just as the nature of disjunction requires that, necessarily, if $p$ then $p\vee q$, so the nature of actuality imposes certain requirements that hold necessarily.

The main broadly logical requirement it imposes, we would like to suggest, is that actuality is necessarily world-like. For possible worlds correspond to ways things could have been; and necessarily, the way things actually are is a way they could have been. So necessarily, the way things actually are corresponds to a possible world.

One consequence of this is that

@-Possibility For all $p$, necessarily, if $@p$ then $♢p$

where ‘@’ abbreviates ‘actually’ and ‘$♢$’ expresses (unrestricted) metaphysical possibility.¹⁶ @-Possibility seems completely obvious: what could be more evident than that it is impossible for actuality to be impossible? Now on its own, @-Possibility ensures merely that necessarily every individual proposition that has actuality is possible. It does not ensure that necessarily, actuality as a whole is possible, that is, that necessarily, the propositions that have actuality are possible together. It seems very plausible, however, that the conjunction of all propositions that are actually true is itself actually true. We may therefore close this gap by imposing a principle of closure.

@-Closure Necessarily, for any set of propositions $A$, if $\bigwedge \{@p:p\in A\}$ then $@\bigwedge A$.

Since a multitude of propositions is jointly possible if their conjunction is possible, @-Possibility and @-Closure together ensure that necessarily, actuality as a whole is possible.

The world-like nature of actuality also entails that actuality, like each possible world, is complete.

@-Completeness For all $p$, necessarily, $@p$ or $@\neg p$

If actuality fails to include a given proposition, then it must include its negation. Notice that we are now in a position to derive the useful claim that for all $p$, necessarily, $@\neg p$ iff $\neg @p$. Call this the commutativity of @ and $\neg$. The right-to-left direction of commutativity follows trivially from @-Completeness. For the left-to-right direction: if $@\neg p$, then it must be that $\neg @p$, for if instead $@p$, then by @-Closure and @-Possibility it would be possible that $\neg p\wedge p$.

@-Completeness evidently entails that there is a sense in which actuality necessarily exists:

@-Existence Necessarily, for some $p$, $@p$.

This consequence strikes us as reasonable. It is also in keeping with the well-known analogy between ‘actually’ and ‘now’. Just as there can be no past or future moment without a corresponding present, so there can be no possible world without a corresponding actuality.

We do not deny that it would be of interest to consider systems in which the assumption of @-Existence is dropped. Such systems would allow for the possibility that actuality might be nonexistent or void—that there might be a possible world at which there are no truths at all of the form ‘$@p$’. But the resulting logic would be very weak. If actuality could have been void, after all, then there would be no validities at all of the form ‘$@p$’—not even ‘$@(p\to p\vee q)$’ or ‘$@(p\wedge q\to p)$’. In this paper, we shall assume @-Existence.

Of course, one might accept @-Existence and still deny @-Completeness, @-Closure, or even @-Possibility. Perhaps there are interesting philosophical views on which it would be natural to do so. But given that, as we have argued, actuality is world-like, denying @-Possibility is not an option, and so denying @-Completeness or @-Closure will involve the rejection of classical assumptions about what is possible. If @-Completeness is denied, for instance, then for some $p$ it is possible for actuality to include neither $p$ nor its negation. But then there will then be a possible world at which neither $p$ nor its negation holds. Similarly, if @-Closure is denied, then there will be a possible world at which some $p_1,p_2,\dots$ are each individually true but their conjunction is not. In this paper, we assume a classical conception of what is possible. Given that assumption, @-Closure and @-Completeness are then also mandatory.

Because actuality is world-like, any possible actuality corresponds to a possible world. That is, for any collection $C$ of propositions for which it is possible that they are exactly the propositions that are actually true, there is a possible world such that exactly the members of $C$ are true at that world. This point leads to a further consequence of the assumption that actuality is world-like. The actuality operator turns out to be a normal modal operator in the sense that (a) necessarily, every propositional tautology is actually true and (b) necessarily, if $p$ and $p\to q$ are actually true then so is $q$.¹⁷ For take any possible world $w$ that corresponds to some possible actuality. At $w$, every tautology is true; and at $w$, if $p$ and $p\to q$ are true then so is $q$. Since actuality is normal, it follows that actuality is congruential in the sense that, if $p\leftrightarrow q$ is a tautology, then necessarily $@p$ iff $@q$.

Let us call every possible world that corresponds to a possible actuality a possibly actual world. Then every possibly actual world, by definition, is a possible world. But is every possible world also a possibly actual world?

One might think to answer ‘yes’ on the grounds that ‘actually’ is redundant: to say that $p$ is actually true is no different from saying that $p$ is true, and so if some world is possible it must be possibly actual too. But we have (in §1) set this view of ‘actually’ aside.

Indeed, we believe there is a strong reason to answer ‘no’ and to hold that some possible worlds are not possibly actual. The reason is that, in our view, it is part of the nature of actuality that it is stable in the following sense.

@-Stability For all $p$, necessarily, if $@p$ then $@@p$

The actuality of $p$, that is, entails the actuality of ‘actually $p$’. (Note that from @-Stability we can derive the converse claim that for all $p$, necessarily, if $@@p$ then $@p$. Instantiating @-Stability with $\neg p$ we obtain $@\neg p\to @@\neg p$ and so $\neg @@\neg p\to \neg @\neg p$. By the commutativity of @ and $\neg$ we have $@@\neg \neg p\to @\neg \neg p$, which yields $@@p\to @p$ by congruentiality.)

Given @-Stability, we can argue that not every possible world is possibly actual (cf. Glazier 2023). Consider this red tomato. It is possible for it to not be red, even though it is actually red: $♢(\neg R\wedge @R)$. But if every possible world is possibly actual, it follows that $♢@(\neg R\wedge @R)$. By normality we obtain $♢(@\neg R\wedge @@R)$ and so by @-Stability $♢(@\neg R\wedge @R)$. Finally, the commutativity of @ and $\neg$ yields $♢(\neg @R\wedge @R)$, which is inconsistent within the background modal logic.

Why should @-Stability be accepted? The principle is admittedly somewhat harder to think about, and form an opinion on, than the previous principles. Here is one way to bring out its appeal informally. We earlier rejected the thought that the notion of actuality can, no matter where we are in modal space, take us back home. But we might now wish to qualify this denial. Granted, actuality does not always take us back to our home. But perhaps we may say that it always takes us back to some home (and where exactly home is will depend on where in modal space we are starting from).

Now you cannot go home and then, once home, go home again. Or better: if you go home, then it is only in a degenerate sense that you can go home again. Once you are already home, going home again changes nothing. Whatever conditions will prevail as a result of your going home will continue to prevail if you go home again. And so if $@p$ is true, so is $@@p$.

It may also help to mention some equivalent principles. A minor variant is this: For all $p$, necessarily, $@(p\to @p)$.¹⁸ This formulation suggests a certain picture of @-Stability as requiring a kind of conditional commitment on the part of any putative actuality: if it is going to say $p$, it is committed to following through and also saying $@p$, and $@@p$, and so on. Actuality, we might say, is by its very nature a place where whatever is true is also actually true.

Another equivalent principle makes use of the notion of necessity given actuality, which we symbolize with ‘$⊡$’. Necessity given actuality is a restricted form of necessity: $p$ is necessary given actuality at a world $w$ iff $p$ holds at every world that agrees with $w$ on what is actually true. (Compare: $p$ is technologically necessary at a world $w$ iff $p$ holds at every world that shares $w$’s technology.) For the Necessitist, of course, every world is a world that agrees with $w$ on what is actually true, and so necessity and necessity given actuality coincide. But given Contingentism there are worlds that do not agree with $w$ on what is actually true, and so the two notions of necessity come apart.

Now it seems very plausible to us that necessity given actuality should imply actuality: for all $p$, necessarily, $⊡\phi \to @\phi$. The realm of possibilities in which actuality is held fixed should always include actuality itself. Writing $\alpha (w)$ for the world corresponding to $w$’s actuality, this amounts to the claim that at every world $w,\alpha (w)$ must be among those worlds that agree with $w$ with respect to actuality, that is, the world $\alpha \alpha (w)$ corresponding to $\alpha (w)$’s actuality must be the very world $\alpha (w)$ corresponding to $w$’s actuality. But this is precisely what is required for @-Stability.

As a final source of support for @-Stability, we want to point out that it leads to a particularly attractive view of the structure of modal space that we can describe using our three notions of necessity, necessity given actuality, and actuality. We assume that absolute necessity is a matter of truth at all worlds, and thus obeys the modal logic S5. Necessity given actuality is necessity restricted by the accessibility relation of having the same actuality, which is easily seen to be an equivalence relation. So the ‘given actuality’ modality also has an S5 logic. We thus obtain a picture of the totality of all possible worlds as partitioned into many disjoint subsets, one for each possibly actual world $w$, comprising exactly the worlds whose actuality corresponds to $w$. @-Stability then amounts to the condition that every possibly actual world is itself in its associated ‘cell’, since it corresponds to its own actuality.

Using the various combinations of modal operators, we may express various conditions about where in modal space a given statement holds. If we assume @-Stability, as we prove below, there are exactly nine mutually inequivalent such conditions we can express.¹⁹ They can be ordered according to their logical strength as follows,

where downward lines signify (one-way) entailment. (We return to the investigation of modalities in the contingentist system in Section 6 below.)

Due to the unfamiliarity of some of these iterated modalities, one may struggle at first to get a clear grip on what they are saying. We find it helpful to think of them pictorially in terms of the partition of the worlds induced by the relation of sharing an actuality. Thus, imagine the space of worlds as a rectangle, partitioned into many cells. In each cell, there is one world which is that cell’s actual world, that is, the actual world of every member of the cell. Let us colour a world red just in case it satisfies a given formula $\phi$. Then relative to $w$, while $\square \phi$ says that the whole space is red, $⊡\phi$ only says that $w$’s cell is completely red. $♢⊡\phi$ says that some cell is red, $♢@\phi$ that the actual world of some cell is red, and $♢\phi$ just that some world in some cell is red. Or to take a different path from top to bottom: while $\square \phi$ says that the whole space is red, $\square @\phi$ says just that the actual world of each cell is red. $@\phi$ says just that the actual world of $w$’s cell is red, $⟐\phi$ that some world in $w$’s cell is red, and $♢\phi$ again that some world in some cell is red.

So we think there is good reason to endorse @-Stability. Still, since the principle seems more contentious to us than those which simply capture the world-like nature of actuality, we shall below also answer the question of the logic of contingent actuality without the assumption of @-Stability.

Before turning to this task, there is a loose end we need to tie up. The machinery we have developed so far supports a certain kind of modal comparison. It allows us to compare what is actually the case with what is necessary or possible given actuality, and so with what is true at other worlds within our cell. We think that typical modal comparisons, including (1), are of this kind. But sometimes we might want to compare what is actually the case with what is true at other worlds generally, including the ones outside our cell. For instance, return to our example of how many dinosaurs there are. There are actually zero dinosaurs, but we argued that there is a possible world at which there are actually some positive number of dinosaurs—say one million. This is not a world that is possible given actuality—it is not a world that lies within our cell—but it is still a possible world. We might want to compare what is the case at this world with what is actually the case.

The problem is how to do it. We might try to say something like, ‘There could have actually been more dinosaurs.’ But this sentence does not make our comparative thought fully explicit. There could have actually been more dinosaurs … than what? The answer might seem to be: than there actually are. But that is false, since there is no possible world at which there are actually more dinosaurs than there actually are.

Some further device is required. A straightforward option, at least in the present case, is to appeal to our ‘at home’ operator, which sends us back to our own dinosaur-free world no matter how far we roam. We can then state our comparative thought by saying that there could have actually been more dinosaurs than there are at home. Discussion of alternative options we leave for another time.

4. Logics of Actuality

Turning now to the formal study of the logic of contingent actuality, we are immediately confronted with the choice of whether to work with a propositional language or a first-order language. From a purely formal point of view, there is some reason for adopting a propositional approach. For the formal logic of quantification looks much the same in a Contingentist setting as it does in the more familiar Necessitist setting. And so a first-order approach risks introducing complexity that distracts from what, from a formal perspective, is truly of interest. But we think that, all things considered, this is a risk worth running. For the logic of actuality is of interest not only on formal grounds but on philosophical grounds as well. Much of the philosophical interest derives from the seeming indispensability of the notion of actuality for stating all of the claims we may wish to state. And the most striking examples of such claims are quantificational, such as ‘there could have been things that don’t actually exist’.²⁰ Moreover, many philosophical debates involving actuality are conducted in a first-order setting. Fara and Williamson (2005: 8), for example, appeal to ‘a standard quantified modal logic with an actuality operator’, and they declare themselves ‘unimpressed by rejections of standard logic that are not accompanied by a properly worked out alternative’. We aim to provide one such alternative.

We therefore assume a fixed standard first-order quantificational language with identity with primitive operators $\neg ,\vee ,\forall$. The language of actuality $ℒ$ results from extending that language by the three modal one-place operators $@,\square$, and $⊡$.

Before introducing our preferred semantics for that language, let us briefly recall the standard way to interpret the actuality operator within a possible world semantics: one picks a unique element $w_0$ from the set of all worlds as the actual, or designated world of the model, and then takes $@\phi$ to be true at a world $w$ iff $\phi$ is true at $w_0$. Since the truth-conditions of $@\phi$ are thus independent of the world under consideration, Necessitism turns out valid, that is, every instance of Necessitism is true at every world of every model of the sort described.

The specification of a designated world also allows one to define a notion of truth simpliciter (in a model) as truth at the designated world. Building on this notion, one may then introduce a second notion of validity as truth in all models. Following Crossley and Humberstone (1977), we may call a formula generally valid iff it is true at every world of every model, and real-world valid iff it is true in (the designated world of) every model. Obviously, general validity entails real-world validity. But the converse does not hold. In particular, every instance of $\phi \leftrightarrow @\phi$ will turn out real-world valid though not generally valid. Still, we have the straightforward connection that $\phi$’s real-world validity is equivalent to $@\phi$’s general validity.

Since we wish to allow actuality to be contingent, we cannot interpret @ by simply, and world-independently, picking one designated world. Instead, we include in our models a function $\alpha$ mapping each world to (the world representing) its actuality, and take $@\phi$ to be true at world $w$ iff $\phi$ is true at $\alpha (w)$. Note that this is strictly a generalization of the previous treatment of @, which corresponds to the special case in which $\alpha$ is a constant function, assigning the same actuality to every possible world. By allowing $\alpha (w)$ to vary for varying $w$, we invalidate the Necessitist principle $@\phi \to \square @\phi$.

We cannot, in terms of $\alpha$ alone, define a notion of truth simpliciter in a model, since $\alpha$ does not in general identify any single world as home, as the world at which all and only the truths hold. What $\alpha$ does provide, though, is a class of worlds that are possibly actual: these are exactly the worlds which are the value of $\alpha$ for some world as argument. This gives rise to an intermediate standard of validity, as truth in all possibly actual worlds of every model; call this a-validity. Under the assumption of Necessitism, this is of course equivalent to truth in the designated world of every model, but in our more general setting it is not. Nor is it equivalent to general validity: $\square @\phi \to \phi$ is an a-validity but not a general validity. Indeed, it is easy to verify that $\phi$ will be a-valid iff $@\phi$ is generally valid.

To define truth in a model, and real-world validity, we may also single out one of the possibly actual worlds of a model as the model’s home world, the designated world. We then obtain three standards of validity relative to a class of models: general validity, a-validity, and real-world validity. General validity obviously implies both a-validity and real-world validity, and as we have seen, a-validity does not imply general validity. Given that the designated world is chosen from among the possibly actual worlds, a-validity implies real-world validity. And as long as we do not make any special assumptions about the designated world beyond this, the converse also holds, and real-world validity implies a-validity.

However, since home is where the truths hold, and since it is agreed on all sides that all instances of $\phi \to @\phi$ are true, it would seem very plausible to demand not only that the designated world be some world’s actuality, but also that be its own actuality, so that $\alpha (w_0)=w_0$. Whether imposing this condition gives rise to real-world validities which are not a-validities depends on whether other possibly actual worlds are allowed to be distinct from their own actuality. And this is equivalent to the question whether @-Stability should be generally valid. For the condition that all possibly actual worlds are their own actualities is the condition that $\alpha \alpha (w)=\alpha w$ for all worlds $w$, which is exactly what is required for $@\phi \to @@\phi$ to hold at every world of every model.

Let us make this more precise. A (standard) frame for $ℒ$ is any pair $(W,\alpha )$ with $W$ a non-empty set and $\alpha :W\to W$ a function from $W$ into $W$. A (standard) model for $ℒ$ is a tuple $(W,D,\alpha ,I)$ where $(W,\alpha )$ is a frame for $ℒ$, $D$ is a non-empty set, and $I$ maps every constant $c$ in $ℒ$ to a member $I(c)$ of $D$, and every pair of n-place predicate $P^n$ in $ℒ$ and world $w\in W$ to a subset of $D^n$.²¹ We call a frame @-stable iff it satisfies the condition that $\alpha \alpha w=\alpha w$ for all worlds of the frame, and we call a model @-stable iff its underlying frame is. If $(W,\alpha )$ is a frame and $w_0\in W$ is such that $\alpha w_0=w_0$, then $(W,\alpha ,w_0)$ is a pointed frame, and if $(W,D,\alpha ,I)$ is a model and $(W,\alpha ,w_0)$ a pointed frame, then $(W,D,\alpha ,I,w_0)$ is a pointed model. Pointed frames and models are called @-stable iff their unpointed counterparts are.

We turn to the definition of satisfaction. Let $M$ be a model $(W,D,\alpha ,I)$; the definition is the same for pointed models. An assignment on $M$ for $ℒ$ is any function $g$ mapping each variable of $ℒ$ to an element of $D$. If $x$ is a variable of $ℒ$ and $o\in D,g_o^x$ is the assignment that assigns $o$ to $x$ and is otherwise just like $g$. If $t$ is a term (i.e., a variable or an individual constant) of $ℒ$ and $g$ an assignment, $d_g(t)=I(t)$ if $t$ is an individual constant and $d_g(t)=g(t)$ if $t$ is a variable. Then, if $\phi$ is any formula of $ℒ$, $w\in W$, and $g$ an assignment on $M$:

• $(M,w,g)\models P^n{t}_1\dots t_n$ iff $(d_g(t_1),\dots ,d_g(t_n))\in I(P^n,w)$

• $(M,w,g)\models t_1=t_2$ iff $d_g(t_1)=d_g(t_2)$

• $(M,w,g)\models \neg \phi$ iff $(M,w,g)\cancel{\models }\phi$

• $(M,w,g)\models (\phi \vee \psi )$ iff $(M,w,g)\models \phi$ or $(M,w,g)\models \psi$

• $(M,w,g)\models \forall x\phi$ iff $(M,w,g_o^x)\models \phi$ for all $o\in D$

• $(M,w,g)\models @\phi$ iff $(M,\alpha (w),g)\models \phi$

• $(M,w,g)\models \square \phi$ iff $(M,v,g)\models \phi$ for all $v\in W$

• $(M,w,g)\models ⊡\phi$ iff $(M,v,g)\models \phi$ for all $v\in W$ with $\alpha v=\alpha w$

A formula $\phi \in ℒ$ is said to be true at a world $w$ in $M((M,w)\models \phi )$ iff $(M,w,g)\models \phi$ for every assignment $g$ on $M$; $\phi$ is true in a pointed model $M$ iff $\phi$ is true at $w_0$. Furthermore, for $\phi \in ℒ$,

• $\phi$ is generally valid in a model $M$ for $ℒ(M\models \phi )$ iff $(M,w)\models \phi$ for all worlds $w$ in $M$

• $\phi$ is a-valid in a model $M$ for $ℒ(M{\models }^A\phi )$ iff $(M,w)\models \phi$ for all worlds $w$ in $M$ such that $w=\alpha v$ for some world $v$ in $M$

• $\phi$ is generally valid (a-valid) on a frame $F$ for $ℒ({\models }_F\phi ,{\models }_F^A\phi )$ iff valid (a-valid) in every model based on $F$

• $\phi$ is real-world valid on a pointed frame $F$ for $ℒ({\models }_F^R\phi )$ iff true in every pointed model based on $F$

• $\phi$ is generally valid (a-valid) on a class $\mathcal{C}$ of frames for $ℒ({\models }_{\mathcal{C}}\phi ,{\models }_{\mathcal{C}}^A\phi )$ iff generally valid (a-valid) on every frame in $\mathcal{C}$

• $\phi$ is real-world valid on a class $\mathcal{C}$ of pointed frames for $ℒ({\models }_{\mathcal{C}}^R\phi )$ iff valid on every frame in $\mathcal{C}$

When we speak of validity without further qualification, we shall always mean general validity. When $\Phi$ is a set of formulas of $ℒ,\Phi$ will be said to be true at a world (true in a model, …) iff every one of its members is. (The use of $\models$ will be extended accordingly.) Furthermore, to each of the three notions of validity corresponds a notion of consequence as truth-preservation at all worlds (all possibly actual worlds, the designated world) of every model in the relevant class, and we shall also use $\models$ for these consequence relations in the usual way.

Within this semantics we can substantiate and make more precise the claim, made above, that it is consistent with our view that for @-free propositions, possibility is equivalent to possibility given actuality. Roughly, the idea is to present a model in which whenever $♢\phi$ is true for @-free $\phi$, also $⟐\phi$ is true. Now, by itself, the existence of such a model does not demonstrate much. After all, there are also necessitist models in our semantics. But we can give a model of the desired sort in which, at the same time, actuality is highly contingent. Indeed, it is contingent to the extent that for all @-free $\phi$ and $\psi$, if $\phi$ and $\psi$ are both individually possible, then it is possible that $\phi \wedge @\psi$.

Call a literal any triple $(P,s,o)$ where for some $n$, P is a (non-logical) $n$-place predicate of $ℒ,s$ is either $\in$ or $\notin$, and $o$ is an $n$-tuple of individual constants of $ℒ$. Call a set of literals consistent (complete) iff for each $n$-place predicate $P$ and $n$-tuple $o$, it contains at most (at least) one of $(P,\in ,o)$ and $(P,\notin ,o)$. Let $S$ be the set of all complete and consistent sets of literals. Now consider the model $M\text{=}(W,D,\alpha ,I)$ such that $W\text{=}S\text{×}S,D(w)$ is the set of all individual constants for all $w\in W,\alpha (w)\text{=}(w[2],w[2])$, and $I(P^n,w)\text{=}\{(t_1,\dots ,t_n):(P^n,\in ,(t_1,\dots ,t_n))\in w[1]\}$ (using $w[i]$ denotes a tuple’s $i$-th coordinate). It is readily verified that $M$ is an @-stable model for $ℒ$. Clearly, for all @-free formulas $\phi$ of $ℒ$, whether $(M,w,g)\models \phi$ depends only on $w[1]$, not on $w[2]$. So suppose that $(M,w,g)\models ♢\phi$, with $\phi$ @-free, and let $v$ be such that $(M,v,g)\models \phi$. Then $(M,(v[1],w[2]),g)\models \phi$, and hence $(M,w,g)\models ♢@\phi$. Moreover, let $\phi$ and $\psi$ be @-free and assume $(M,w,g)\models ♢\phi$ and $(M,w,g)\models ♢\psi$. Let $(M,v,g)\models \phi$ and $(M,u,g)\models \psi$. Then $(M,(v[1],u[1]),g)\models \phi \wedge @\psi$.

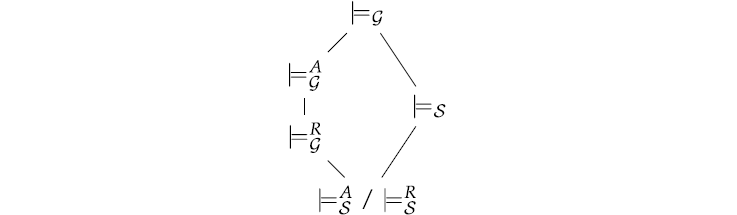
We turn now to the task of determining the logics of actuality our semantic framework yields. We shall consider the relations of general, a-, and real-world consequence both for the most general class of frames and for the class of @-stable frames. We shall use $\mathcal{G}$ ambiguously both for the class of all (unpointed) frames and the class of all pointed frames, depending on which consequence relation is at issue, and we shall similarly use $\mathcal{S}$ for the classes of unpointed or pointed @-stable frames. The next section will show how to axiomatize these relations. But even before that, we can make some useful observations regarding their interrelations, many of which have already been hinted at above. They can be summarized in a diagram as follows. (The claims apply both at the level of validity and at the level of consequence.)

Here downward lines signify proper subsethood; thus, for example, the set of formulas $\phi$ with ${\models }_{\mathcal{G}}\phi$ is a proper subset of the set of formulas $\phi$ with ${\models }_{\mathcal{G}}^A\phi$. As suggested above, the a-validities and the real-world validities on @-stable frames are the same, since in @-stable frames, there is nothing special about the designated world in comparison to any other possibly actual world.

The inclusion parts of these claims of proper inclusion are straightforward from the definitions. To show that the inclusion relationships are proper, we provide the following examples. Let $p$ be some atomic predication $P^{1}t$ of $ℒ$.

• $@p\leftrightarrow p$ is a-valid but not generally valid on $\mathcal{S}$

• $@p\to @@p$ is generally valid on $\mathcal{S}$ but not on $\mathcal{G}$

• $\square (@p\to @@p)$ is a-valid on $\mathcal{S}$ but not real-world valid on $\mathcal{G}$

• $@p\leftrightarrow p$ is real-world valid but not a-valid on $\mathcal{G}$

• $\square @p\to p$ is a-valid but not generally valid on $\mathcal{G}$

5. Axiomatization

We shall use the following set of non-modal axiom schemata and rules:

We will now extend it by suitable axioms and rules for each of our three modalities, and finally add suitable interactive axioms governing the interrelation between the modalities. For @, the axioms and rules are

(@K) and (@Nec) hold simply in virtue of the fact that @ may be seen as a normal modality, that is, as a necessity-like operator evaluated in terms of a particular accessibility relation. For we may regard the $\alpha$-function as a functional accessibility relation, and then $@\phi$ will be true iff $\phi$ holds in all $\alpha$-accessible worlds. The first two axiom schemata correspond to the structural features the accessibility relation corresponding to $\alpha$ has. Since $\alpha$ is a total function on the set of worlds, every world can access some world, corresponding to (@Con).²² Since $\alpha$ is a total function, every world can access at most one world, corresponding to (@Cpl).²³ (@BF) is ensured by the fact that we are using constant domains.

For both $\square$ and $⊡$, the axioms and rules are simply the usual S5 axioms and rules for constant domain semantics

We shall refer to the system of axioms and rules given so far as our base system ${\mathrm{\text{CA}}}_{@}$, and to its extension by the 4 axiom schema for @

as ${\mathbf{\text{CA}}}_{@}^{\text{+}}$. The system ${\mathbf{\text{CA}}}_{@}\mathbf{\text{I}}$ is obtained by extending ${\mathbf{\text{CA}}}_{@}$ by these interaction axioms

registering the fact @ and $⊡$ are restricted versions of, and therefore subsume, the $\square$-modality, as well as the rigidity of @ with respect to $⊡$.²⁴

Finally, we call ${\mathbf{\text{CA}}}_{@}{\mathbf{\text{I}}}^{\text{+}}$ the result of extending ${\mathbf{\text{CA}}}_{@}\mathbf{\text{I}}$ by the additional subsumption schema for $⊡$ and @:

Note that (@4) is derivable within this system by combining ($@⊡$-Rig) and ($⊡@$-Sub), so adding it would not yield anything new.

If $\mathbf{\text{S}}$ is any of our sets of axioms and rules and if $\phi \in ℒ$, we write ${⊢}_{\mathrm{\text{S}}}\phi$ to say that $\phi$ is provable within $\mathbf{\text{S}}$, that is, that $\phi$ belongs to the smallest subset of $ℒ$ which contains every $ℒ$-instance of an axiom schema in $\mathbf{\text{S}}$ and is closed under the rules in $\mathbf{\text{S}}$. For $\Gamma \subseteq ℒ$, we write $\Gamma {⊢}_{\mathrm{\text{S}}}\phi$ to say that for some finite number of elements ${\psi }_1,\dots ,{\psi }_n$ of $\Gamma ,{⊢}_{\mathrm{\text{S}}}({\psi }_1\wedge \dots \wedge {\psi }_n)\to \phi$.

In terms of these systems of axioms and rules, we can axiomatize our five consequence relations (and sets of validities) within $ℒ$. We first consider the general consequence relation on all frames, and on @-stable frames. As we will show below, for $\Gamma \cup \phi \subseteq ℒ$,

• $\Gamma {\models }_{\mathcal{G}}\phi$ iff $\Gamma {⊢}_{{\mathrm{\text{CA}}}_{@}\mathrm{\text{I}}}\phi$

• $\Gamma {\models }_{\mathcal{S}}\phi$ iff $\Gamma {⊢}_{{\mathrm{\text{CA}}}_{@}{\mathrm{\text{I}}}^{\text{+}}}\phi$

To axiomatize a-consequence and real-world consequence, we proceed as follows. Call $PA$—for ‘possibly actual’—the set of all $ℒ$-instances of the schema $\phi \to ♢@\phi$ as well as their universal closures, and call $D$—for ‘designated’—the set of all $ℒ$-instances of $@\phi \leftrightarrow \phi$ as well as their universal closures.²⁵ We shall prove below that

• $\Gamma {\models }_{\mathcal{G}}^A\phi$ iff $\Gamma \cup PA{⊢}_{{\mathrm{\text{CA}}}_{@}\mathrm{\text{I}}}\mathit{\phi }$

• $\Gamma {\models }_{\mathcal{G}}^R\phi$ iff $\Gamma \cup D{⊢}_{{\mathrm{\text{CA}}}_{@}\mathrm{\text{I}}}\phi$

• $\Gamma {\models }_{\mathcal{S}}^A\phi$ iff $\Gamma \cup PA{⊢}_{{\mathrm{\text{CA}}}_{@}{\mathrm{\text{I}}}^{\text{+}}}\mathit{\phi }$

• $\Gamma {\models }_{\mathcal{S}}^R\phi$ iff $\Gamma \cup PA{⊢}_{{\mathrm{\text{CA}}}_{@}{\mathrm{\text{I}}}^{\text{+}}}\mathit{\phi }$

6. Iterated Modalities

We call an iterated modality any (finite, non-zero) string of symbols, each of which is either $\square ,♢,⊡,⟐$, or @. Some iterated modalities are equivalent to others, which raises the question if we can characterize an interesting set of iterated modalities such that every iterated modality is equivalent to one in the set. If a set of iterated modalities satisfies this condition, let us call it complete. In our context, the answer depends strongly on whether we assume @-stability.

Let us call $\square$ and $♢$ the unrestricted modalities and $⊡$ and $⟐$ the a-modalities. We then note that,

Lemma 1. Within ${\mathbf{\text{CA}}}_{@}\mathbf{\text{I}}$,

1. $\square \phi$ implies $o\phi$, for any (single²⁶) modality $o$

2. $o\phi$ implies $♢\phi$, for any modality $o$

3. $ou\phi$ is equivalent to $u\phi$ for any modality $o$ and unrestricted modality $u$

4. $o@\phi$ is equivalent to $@\phi$ whenever $o$ is an a-modality

5. $\square ⊡\phi$ is equivalent to $\square \phi$

6. $♢⟐\phi$ is equivalent to $♢\phi$

Proof. 1. is immediate from the subsumption axioms and the fact that both ‘box’-modalities imply their ‘diamond’ counterparts. For 2., the same holds, except that in the case of $o=@$, we also need to use (@Con). 3. may then be established using 1. and 2. and the fact that, by the S5 axioms, $u\phi$ implies $\square u\phi$ and $♢u\phi$ implies $u\phi$. 4. is immediate from the rigidity axiom for @ wrt $⊡$ and ($⊡$T).

For 5., that $\square ⊡\phi$ implies $\square \phi$ is shown using the necessitation of ($⊡$T) and ($\square$K). For the converse, $\square \phi$ implies $\square \square \phi$ by S5, which implies $\square ⊡\phi$ by the necessitation of ($\square ⊡$Sub). The proof of 6. follows a similar pattern.

Lemma 2. Every iterated modality is equivalent within ${\mathrm{\text{CA}}}_{@}\mathrm{\text{I}}$ to one of the form $u{@}^{n}a$, where u is either null or an unrestricted modality, ${@}^n$ is a sequence, of finite length $n\ge 0$, of occurrences of @, and a is null or an a-modality.

Proof. Given lemma 1(3), any iterated modality is equivalent to its shortest final segment $u{o}_1\dots o_m$ starting with an unrestricted modality. By lemma 1(4), we may delete within $o_1\dots o_m$ any sequence of a-modalities that is followed by an occurrence of @, thereby simplifying the iterated modality to one of the shape $u{@}^n{a}_1\dots a_j$. Since the a-modalities are S5 modalities, $a_1\dots a_j$ simplifies to $a_j$, so we obtain the desired shape of $u{@}^{n}a$.

Once we assume @-stability and move to the system ${\mathbf{\text{CA}}}_{@}{\mathbf{\text{I}}}^{\text{+}}$, iterations of @ become redundant, and we obtain a finite and indeed fairly small complete set of iterated modalities.

Lemma 3. Within ${\mathbf{\text{CA}}}_{@}{\mathbf{\text{I}}}^{\text{+}}$,

1. ${@}^n\phi$ is equivalent to $@\phi$ whenever $n>0$

2. $@a\phi$ is equivalent to $a\phi$ for any a-modality $a$

Proof. For 1., we show that $@\phi$ is equivalent to $@@\phi$; the stronger claim then follows easily. $@\phi$ implies $⊡@\phi$ by ($@⊡$-Rig), which implies $@@\phi$ by ($⊡@$Sub). $\neg @\phi$ implies $@\neg \phi$ by (@Cpl), which implies $@@\neg \phi$ by the previous reasoning, which implies $\neg @@\phi$ via two applications of (@Con).

For 2.: $⊡\phi$ implies (by S5) $⊡⊡\phi$, implies (by ($⊡@$Sub)) $@⊡\phi$, and $\neg ⊡\phi$ implies (by S5) $⊡\neg ⊡\phi$, implies (by ($⊡@$Sub)) $@\neg ⊡\phi$, implies (by (@Con)) $\neg @⊡\phi$. The case of $⟐$ is similar.

Lemma 4. Every iterated modality is equivalent within ${\mathbf{\text{CA}}}_{@}{\mathbf{\text{I}}}^{\text{+}}$ to one of the following nine: $\square ,♢,⊡,⟐,@,\square @,♢@,\square ⟐,♢⊡$.

Proof. From lemma 2 and the redundancy of @-iterations within ${\mathbf{\text{CA}}}_{@}{\mathbf{\text{I}}}^{\text{+}}$ it is clear that every iterated modality reduces to one of the seventeen iterated modalities of the form $u{@}^{✻}a$, where $u$ is null or an unrestricted modality, ${@}^{✻}$ is null or @, $a$ is null or an a-modality, and at least one of $u,{@}^{✻}$, and $a$ is not null. In addition, by lemma 3(2), @ is redundant in all of $@⊡,@⟐,\square @⊡,\square @⟐,♢@⊡$, and $♢@⟐$, so these reduce to $⊡,⟐,\square ⊡,\square ⟐,♢⊡$, and $♢⟐$, respectively. Finally, by lemma 1(5)–(6), $\square ⊡$ is equivalent to $\square$, and $♢⟐$ to $♢$, bringing the set down to the nine iterated modalities above.

7. Soundness and Completeness

The soundness proofs are relatively straightforward.

Theorem 5.

1. $\Gamma {\models }_{\mathcal{G}}\phi$ if $\Gamma {⊢}_{{\mathrm{\text{CA}}}_{@}\mathrm{\text{I}}}\phi$

2. $\Gamma {\models }_{\mathcal{S}}\phi$ if $\Gamma {⊢}_{{\mathrm{\text{CA}}}_{@}{\mathrm{\text{I}}}^{\text{+}}}\phi$

3. $\Gamma {\models }_{\mathcal{G}}^A\phi$ if $\Gamma \cup PA{⊢}_{{\mathrm{\text{CA}}}_{@}\mathrm{\text{I}}}\phi$

4. $\Gamma {\models }_{\mathcal{G}}^R\phi$ if $\Gamma \cup D{⊢}_{{\mathrm{\text{CA}}}_{@}\mathrm{\text{I}}}\phi$

5. $\Gamma {\models }_{\mathcal{S}}^A\phi$ if $\Gamma \cup PA{⊢}_{{\mathrm{\text{CA}}}_{@}{\mathrm{\text{I}}}^{\text{+}}}\mathit{\phi }$

6. $\Gamma {\models }_{\mathcal{S}}^R\phi$ if $\Gamma \cup PA{⊢}_{{\mathrm{\text{CA}}}_{@}{\mathrm{\text{I}}}^{\text{+}}}\mathit{\phi }$

Proof. The proofs are by induction on the length of derivations in the relevant deductive systems. The key is to prove that the axioms of the system under consideration are valid in the appropriate sense, and that the rules of the system preserve validity in that sense.

For 1., we need to establish for ${\mathbf{\text{CA}}}_{@}\mathbf{\text{I}}$ that all axioms are generally valid, and that all its rules preserve general validity, in all models of all frames of our semantics. For the axioms and rules of ${\mathrm{\text{CA}}}_{@}$, this is a standard fact, given that $\square$ is interpreted by the universal accessibility relation, @ is interpreted by a total functional relation, and $⊡$ is interpreted by the equivalence relation of sharing an actuality. Turning to the interaction axioms, the general validity of the subsumption axioms relating $\square$ to $⊡$ and to @ are also obvious. Slightly less trivial is the case of the rigidity axiom $@\phi \to ⊡@\phi$, but

$\begin{array}{ll}(M,w)\models @\phi \hfill & \to (M,\alpha w)\models \phi \hfill \\ \hfill & \to (M,\alpha v)\models \phi \text{\hspace{0.17em}whenever\hspace{0.17em}}\alpha v=\alpha w\hfill \\ \hfill & \to (M,v)\models @\phi \text{\hspace{0.17em}whenever }\alpha v=\alpha w\hfill \\ \hfill & \to (M,w)\models ⊡@\phi \hfill \end{array}$

For 2., we need to establish the general validity of the axioms, and preservation of general validity by the rules, of ${\mathbf{\text{CA}}}_{@}{\mathbf{\text{I}}}^{\text{+}}$ on the class of all models of @-stable frames. The only additional axiom we have to consider here is the axiom ($⊡@$Sub) subsuming @ under $⊡$. Its validity on @-stable frames may be established as follows, using the fact that $\alpha \alpha w=\alpha w$ in all such frames:

For 3., recall that $PA$ is the set of all $ℒ$-instances of the schema $\phi \to ♢@\phi$ as well as their universal closures. It is easily verified that every member of $PA$ is true at every possibly actual world of any model. Now assume that $\Gamma \cup PA{⊢}_{{\mathrm{\text{CA}}}_{@}\mathrm{\text{I}}}\phi$. We need to show that $\phi$ is true in every possibly actual world of any model in which all members of $\Gamma$ are true. So suppose $w$ is a possibly actual world of some model in which all members of $\Gamma$ are true. Then every member of $PA$ is true at $w$, so every member of $\Gamma \cup PA$ is true at $w$. By 1., we know that $\phi$ is true in every world of every model in which all members of $\Gamma \cup PA$ are true. So it follows that $\phi$ is true in $w$, as required.

For 4., recall that $D$ is the set of all $ℒ$-instances of the schema $@\phi \leftrightarrow \phi$ as well as their universal closures. It is easily verified that every member of $D$ is true at every designated world of any pointed model. Using this fact and reasoning in parallel to before, we may infer from the assumption that $\Gamma \cup D{⊢}_{{\mathrm{\text{CA}}}_{@}\mathrm{\text{I}}}\phi$ that $\phi$ is true in every designated world of any model in which all members of Γ are true, as required.

The reasoning for 5. and 6. is analogous, restricting attention to @-stable frames, and in the case of 6. using the fact that the designated world of every pointed model is possibly actual.

For proving completeness we make use of a generalized semantics for $ℒ$, in which the three modalities are interpreted by separate accessibility relations.

Definition 1. We call a

• generalized frame for $ℒ$ any tuple $(W,R_{@},R_{\square },R_{⊡})$, where $W$ is a non-empty set and $R_{@},R_{\square }$, and $R_{⊡}$ are subsets of $W^2$

• generalized model for $ℒ$ any tuple $(W,D,R_{@},R_{\square },R_{⊡},I)$ with $D$ a non-empty set, $I$ an interpretation function, and $(W,R_{@},R_{\square },R_{⊡})$ a generalized frame

• semi-generalized frame for $ℒ$ any tuple $(W,R_{@},R_{⊡})$, where $W$ is a non-empty set and $R_{@}$ and $R_{⊡}$ are subsets of $W^2$

• semi-generalized model for $ℒ$ any tuple $(W,D,R_{@},R_{⊡},I)$ with $(W,R_{@},R_{⊡})$ a semi-generalized frame, $D$ a non-empty set, and $I$ an interpretation function

Satisfaction in generalized models is defined in the obvious way, with $@,\square$, and $⊡$ interpreted respectively as truth in all $R_{@}$-, $R_{\square }$-, or $R_{⊡}$-accessible worlds. Satisfaction in semi-generalized models is defined in the same way but interpreting $\square$ as truth in all worlds.

Theorem 6. For every $\Gamma \subseteq ℒ$ consistent within ${\mathrm{\text{CA}}}_{@}$, there is a generalized model $M=(W,D,R_{\square },R_{⊡},R_{@},I)$ and world $w_0\in W$ with $(M,w_0)\models \Gamma$, in which $R_{@}$ is a total function, and $R_{\square }$ and $R_{⊡}$ are equivalence relations.

Proof. This follows from theorem 4.2 in Schurz (2011).

As Schurz’s proof makes clear, we can construct such a generalized model in the usual way: we form an extended language ${ℒ}^{\text{+}}$ with enough additional individual constants to witness all the existential quantifications in $\Gamma$, and extend $\Gamma$ to a maximally consistent and fully witnessed subset $\Delta$ of ${ℒ}^{\text{+}}$. The worlds of the canonical model are exactly the maximally consistent subsets of ${ℒ}^{\text{+}}$ that respect the identity-statements in $\Delta$. The accessibility relations of the model are then defined by letting $R_{\square }wv$ hold iff $v\subseteq \{\phi \in {ℒ}^{\text{+}}:\square \phi \in w\}$, and analogously for $R_{@}$ and $R_{⊡}$. In what follows, we shall assume that the generalized models under consideration are of this sort.

We shall now show how, in a two-step process, any generalized model (for an extension ${ℒ}^{\text{+}}$ of $ℒ$) which validates ${\mathbf{\text{CA}}}_{@}\mathbf{\text{I}}$—that is, in which all the theorems of ${\mathbf{\text{CA}}}_{@}\mathbf{\text{I}}$ are true at every world—may be transformed into a corresponding standard model (that is, a model of the sort we defined in §4). In the first step, we define a corresponding semi-generalized model.

Definition 2. Let $M=(W,D,R_{\square },R_{⊡},R_{@},I)$ be a generalized model with $w_0\in W$ and validating ${\mathbf{\text{CA}}}_{@}\mathbf{\text{I}}$. The semi-generalized model corresponding to $M$ with respect to $w_0$ is $M^{✻}=(W^{✻},D,R_{⊡}^{✻},R_{@}^{✻},I^{✻})$, where

• $W^{✻}$ is the equivalence class of $w_0$ under $R_{\square }$, and

• $R_{⊡}^{✻},R_{@}^{✻},I^{✻}$ result from restricting $R_{⊡},R_{@},I$ to $W^{✻}$.

Lemma 7. Let $M$ be a generalized model with $w_0\in W$ and validating ${\mathbf{\text{CA}}}_{@}\mathbf{\text{I}}$. Let $M^{✻}$ be the semi-generalized model corresponding to $M$ with respect to $w_0$. Then for all $w\in W^{✻},(M,w)\models \phi$ iff $(M^{✻},w)\models \phi$.

Proof. Since $M$ validates ${\mathbf{\text{CA}}}_{@}\mathrm{\text{I}},M$ validates all instances of the subsumption axioms $\square \phi \to ⊡\phi$ and $\square \phi \to @\phi$. Then all worlds in $W$ that are $R_{⊡}$-accessible or $R_{@}$-accessible from any world in $W^{✻}$ are also $R_{\square }$-accessible from that world and hence in $W^{✻}$. Using this observation, the claim follows by an easy induction on the complexity of $\phi$.

Note that the worlds of the original, generalized model which are retained in the semi-generalized model are exactly those that include every ${ℒ}^{\text{+}}$-sentence of the form $\square \phi$ that is true at $w_0$.

In the second step, our main task is to eliminate $R_{⊡}$, instead evaluating $⊡$ in terms of the relation of sharing an actuality. Let us use $\alpha$ for the function associated with $R_{@}^{✻}$, so for all $w\in W^{✻},\alpha (w)$ is the unique world $v\in W^{✻}$ with $R_{@}^{✻}wv$. If we could be sure that in $M^{✻},\alpha (w)=\alpha (v)$ holds iff $R_{⊡}^{✻}wv$, our task would be trivial, since re-interpreting $⊡$ in the way described would be guaranteed to preserve truth-values. By the rigidity axiom $@\phi \to ⊡@\phi$, it is clear that $\alpha w=\alpha v$ whenever $R_{⊡}^{✻}wv$. But there is no guarantee that the converse holds: we may have worlds sharing an actuality even though they do not stand in $R_{⊡}^{✻}$. To rectify this, we add new worlds into our model, one for each equivalence class under $R_{⊡}^{✻}$, playing the role of the actual world of the members of that class. In order to leave the evaluation of all formulas intact, we make sure the new worlds are ‘copies’ of the old worlds playing the role of actual world for the same equivalence class.

Definition 3. Let $M^{✻}$ be a semi-generalized model validating ${\mathbf{\text{CA}}}_{@}\mathbf{\text{I}}$. Let $\mathcal{C}$ be the set of equivalence classes under $R_{⊡}^{✻}$, and for $w\in W^{✻}$, let $[w]$ be $w$’s equivalence class under $R_{⊡}^{✻}$. For each $c\in C$, pick some item $a^c$, not in $W^{✻}$, in such a way that for $c_1,c_2\in C$, if $c_1\ne c_2$ then $a^{c_1}\ne a^{c_2}$. Then the standard model corresponding to $M^{✻}$ is $M^{\prime }=(W^{\prime },D,{\alpha }^{\prime },I^{\prime })$ with

• $W^{\prime }=W^{✻}\cup \{a^c:c\in C\}$,

• for all $w\in W^{✻},{\alpha }^{\prime }w=a^{[w]}$, and ${\alpha }^{\prime }(a^{[w]})=a^{[\alpha w]}$,

• $I^{\prime }(c)=I(c)$ for all individual constants c, and

• for all $w\in W^{✻},I^{\prime }(P^n,w)=I(P^n,w)$ and $I^{\prime }(P^n,a^{[w]})=I(P^n,\alpha w)$

Note that every member $w$ of $W^{\prime }$ is either in $W^{✻}$, or of the form $a^{[v]}$, with $v\in W^{✻}$. We make use of this fact in the definition of ${\alpha }^{\prime }$ and $I^{\prime }$, and will often rely on it in subsequent definitions and proofs as well.

In proving the equivalence of corresponding standard and semi-generalized models $M^{✻}$ and $M^{\prime }$, we shall often find it useful to speak, with respect to a given world $w$ in $W^{\prime }$, of its counterpart $o(w)$ among the worlds in $W^{✻}$. If $w$ is not possibly actual, this is simply $w$ itself, and if $w=a^{[v]}$, it is $\alpha v$.

Definition 4. Let the standard model $M^{\prime }$ correspond to a semi-generalized model $M^{✻}$. Then for all $w\in W^{✻}$, let

• the counterpart $o(w)$ of $w$ be $w$, and

• the counterpart $o(a^{[w]})$ of $a^{[w]}$ be $\alpha w$

We first prove two helpful lemmas about $o$ in relation to $\alpha ,{\alpha }^{\prime }$, and $R_{⊡}$.

Lemma 8. Let the standard model $M^{\prime }$ correspond to a semi-generalized model $M^{✻}$. Then for all $w\in W^{\prime },o({\alpha }^{\prime }w)=\alpha o(w)$.

Proof. Let $w\in W^{✻}$. We prove the claim for $w$ and for $a^{[w]}$, thereby establishing it for all $w\in W^{\prime }$.

$\begin{array}{lll}o(\alpha \prime w)\hfill & =o(a^{[w]})\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by df. }{\alpha }^{\prime }\hfill \\ \hfill & =\alpha w\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by df. }o\hfill \\ \hfill & =\alpha o(w)\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}since }w\in W^{*},o(w)=w\hfill \\ o({\alpha }^{\prime }(a^{[w]}))\hfill & =o(a^{[\alpha w]})\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by df. }{\alpha }^{\prime }\hfill \\ \hfill & =\alpha \alpha w\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by df. }o\hfill \\ \hfill & =\alpha o(a^{[w]})\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by df. }o\hfill \end{array}$

Lemma 9. Let the standard model $M^{\prime }$ correspond to a semi-generalized model $M^{✻}$. Then for all $w,v\in W^{\prime },{\alpha }^{\prime }w={\alpha }^{\prime }v$ iff $R_{⊡}o(w)o(v)$.

Proof. We distinguish four cases, depending on whether $w$ and/or $v$ are in $W^{✻}$ or of the form $a^{[u]}$. First, assume $w=a^{[u]}$ and $v=a^{[z]}$. Then

$\begin{array}{lll}{\alpha }^{\prime }w={\alpha }^{\prime }v\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}{\alpha }^{\prime }(a^{[u]})={\alpha }^{\prime }(a^{[z]})\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by assumption}\hfill \\ \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}{a}^{[\alpha u]}=a^{[\alpha z]}\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by df.\hspace{0.17em}}{\alpha }^{\prime }\hfill \\ \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff }{R}_{⊡}\alpha (u)\alpha (z)\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by df.\hspace{0.17em}}{a}^c\hfill \\ \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}{R}_{⊡}o(a^{[u]})o(a^{[z]})\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by df.\hspace{0.17em}}o\hfill \\ \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}{R}_{⊡}o(w)o(v)\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by assumption}\hfill \end{array}$

Next, suppose $w=a^{[u]}$ and $v\in W^{✻}$.

$\begin{array}{lll}{\alpha }^{\prime }w={\alpha }^{\prime }v\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}{\alpha }^{\prime }(a^{[u]})=a^{[v]}\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by assumption, df.\hspace{0.17em}}{\alpha }^{\prime }\hfill \\ \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}{a}^{[\alpha u]}=a^{[v]}\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by df.\hspace{0.17em}}{\alpha }^{\prime }\hfill \\ \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}{R}_{⊡}\alpha (u)v\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by df.\hspace{0.17em}}{a}^c\hfill \\ \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}{R}_{⊡}o(a^{[u]})o(v)\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by df.\hspace{0.17em}}o\hfill \\ \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}{R}_{⊡}o(w)o(v)\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by assumption}\hfill \end{array}$

The case in which $w\in W^{✻}$ and $v=a^{[u]}$ is obviously parallel. Finally, if $w,v\in W^{✻}$, then ${\alpha }^{\prime }w={\alpha }^{\prime }v$ iff (by df. ${\alpha }^{\prime }$) $a^{[w]}=a^{[v]}$ iff (by df. $a^c$) $R_{⊡}wv$ iff $R_{⊡}o(w)o(v)$.

We are now in a position to prove that corresponding semi-generalized and standard models are equivalent in the following sense.

Lemma 10 Let the standard model $M^{\prime }$ correspond to a semi-generalized model $M^{✻}$. Then for all $w\in W^{\prime },(M^{\prime },w)\models \phi$ iff $(M^{✻},o(w))\models \phi$.

Proof. By induction on the complexity of $\phi$. We do the case of $@\phi$ and $⊡\phi$ as they concern the adjusted components of the models; all other cases are entirely straightforward. Let $w\in W^{\prime }$, and suppose (IH) the claim holds for $\phi$.

$\begin{array}{lll}(M^{\prime },w)\models @\phi \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}(M^{\prime },{\alpha }^{\prime }w)\models \phi \hfill & \hfill \\ \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}(M^{✻},o({\alpha }^{\prime }w))\models \phi \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by IH}\hfill \\ \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}(M^{✻},\alpha o(w))\models \phi \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by lemma 8}\hfill \\ \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}(M^{✻},o(w))\models @\phi \hfill & \hfill \end{array}$

$\begin{array}{lll}(M^{\prime },w)\models ⊡\phi \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}(M^{\prime },v)\models \phi \hfill & \hfill \\ \hfill & \text{\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}all\hspace{0.17em}}v\in W^{\prime }\text{\hspace{0.17em}with\hspace{0.17em}}{\alpha }^{\prime }w={\alpha }^{\prime }v\hfill & \hfill \\ \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}(M^{✻},o(v))\models \phi \hfill & \hfill \\ \hfill & \text{\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}all\hspace{0.17em}}v\in W^{\prime }\text{\hspace{0.17em}with\hspace{0.17em}}{\alpha }^{\prime }w={\alpha }^{\prime }v\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by IH}\hfill \\ \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}(M^{✻},o(v))\models \phi \hfill & \hfill \\ \hfill & \text{\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}all\hspace{0.17em}}v\in W^{\prime }\text{\hspace{0.17em}with\hspace{0.17em}}{R}_{⊡}o(w)o(v)\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}by lemma }9\hfill \\ \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}(M^{✻},v)\models \phi \hfill & \hfill \\ \hfill & \text{\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}all\hspace{0.17em}}v\in W^{✻}\text{\hspace{0.17em}with\hspace{0.17em}}{R}_{⊡}o(w)v\hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}since\hspace{0.17em}}o’s\text{\hspace{0.17em}range\hspace{0.17em}is\hspace{0.17em}}{W}^{✻}\hfill \\ \hfill & \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}iff\hspace{0.17em}}(M^{✻},o(w))\models ⊡\phi \hfill & \hfill \end{array}$