Spatial Variation in Flowering Age in Cirsium pitcheri: Does This Imperiled Dune Thistle Hedge Its Bets?

Introduction

For flowering plants, the timing of reproduction is an important fitness component. There is a rich literature exploring the costs and benefits of delaying reproduction (Bell 1980; Roff 1992; Metcalf et al. 2003). For monocarpic (semelparous) plants, many factors may influence the timing of bolting, including environmental factors such as water and nutrient availability, climate, or the size and age of the plant (Metcalf et al. 2003).

Many studies have shown that plants have phenotypic plasticity in the timing at which they flower in response to an outside factor. For example, Klinkhamer et al. (1991) studied the effects of environmental factors on the growth and flowering of the monocarpic perennial species Carlina vulgaris L.. The results showed that for large individuals, a cold period reduced the number of days it took for the plants to flower; without cold treatment, individuals did not flower until reaching a very large size or after many days of enduring long periods of light exposure. In addition, that study posited evidence that plants can respond quite strongly to environmental stimuli.

In evolutionary biology, the conservative bet-hedging strategy is described as the process of risk avoidance on the individual level (Childs et al. 2010). In the case of monocarpic perennial plants, the act of flowering negates the possible future risk of death and is an example of this conservative evolutionary strategy. Although the plant may receive the benefit of a possible increase in fecundity after a year of growth, a plant also faces the risk of death during the following year. Because of this, the act of flowering for these plants is a conservative strategy as it ensures the reproductive success of the plant. Plant species must flower within the optimal timing of reaching the correct benchmark size for maximum reproductive output, but it is difficult to determine this exact size given the variability of most environments.

Some perennial plants have a threshold size that the plant must reach when it has accumulated sufficient resources needed for bolting and flowering (Wesselingh et al. 1997). By delaying flowering until the plant reaches a larger size, a plant is thereby capable of a higher fecundity. However, in delaying flowering, there is an additional risk that the plant will die before reproducing. Lacey (1986) found that a slow growth rate can induce flowering in the short- lived monocarpic perennial Daucus carota L.. Metcalf et al. (2003) describe this relationship as “the law of diminishing returns,” in which the payoff of increased fecundity will diminish as a plant’s growth stops or slows after reaching a certain size, after which they will flower. Depending on resources available to plants within their habitats, there is a resulting variation in the age at flowering due to variation in the time that it takes plants to reach the threshold size for bolting. Through a similar demographic study, Kuss et al. (2008) determined that Campanula thyrsoides L., a long-lived perennial species endemic to forested areas, exhibited a similar strategy whereby these plants showed a decreasing rate of growth as size increased as well as a pronounced threshold size at which the plants flowered. Additionally, Hanzawa and Kalisz (1993) determined that Trillium grandiflorum (Michx.) Salisb., another perennial endemic to wooded areas, flowered only after meeting a threshold leaf area or rhizome volume and that for that species, plant size was a much better indicator for the timing of flowering than a plant’s age.

Nevertheless, it has been shown that for some plant species, there can be variation within a population in both the size and age at which a plant flowers depending on nutrient availability or other environmental factors (Kagaya et al. 2009). This occurs as a result of variable growth rates in response to nutrient availability. For some plants, especially those with high nutrient availability, there can be great plasticity in the size at bolting and flowering. For these species, there is less evidence for a threshold flowering size; the timing of flowering is not dependent on size.

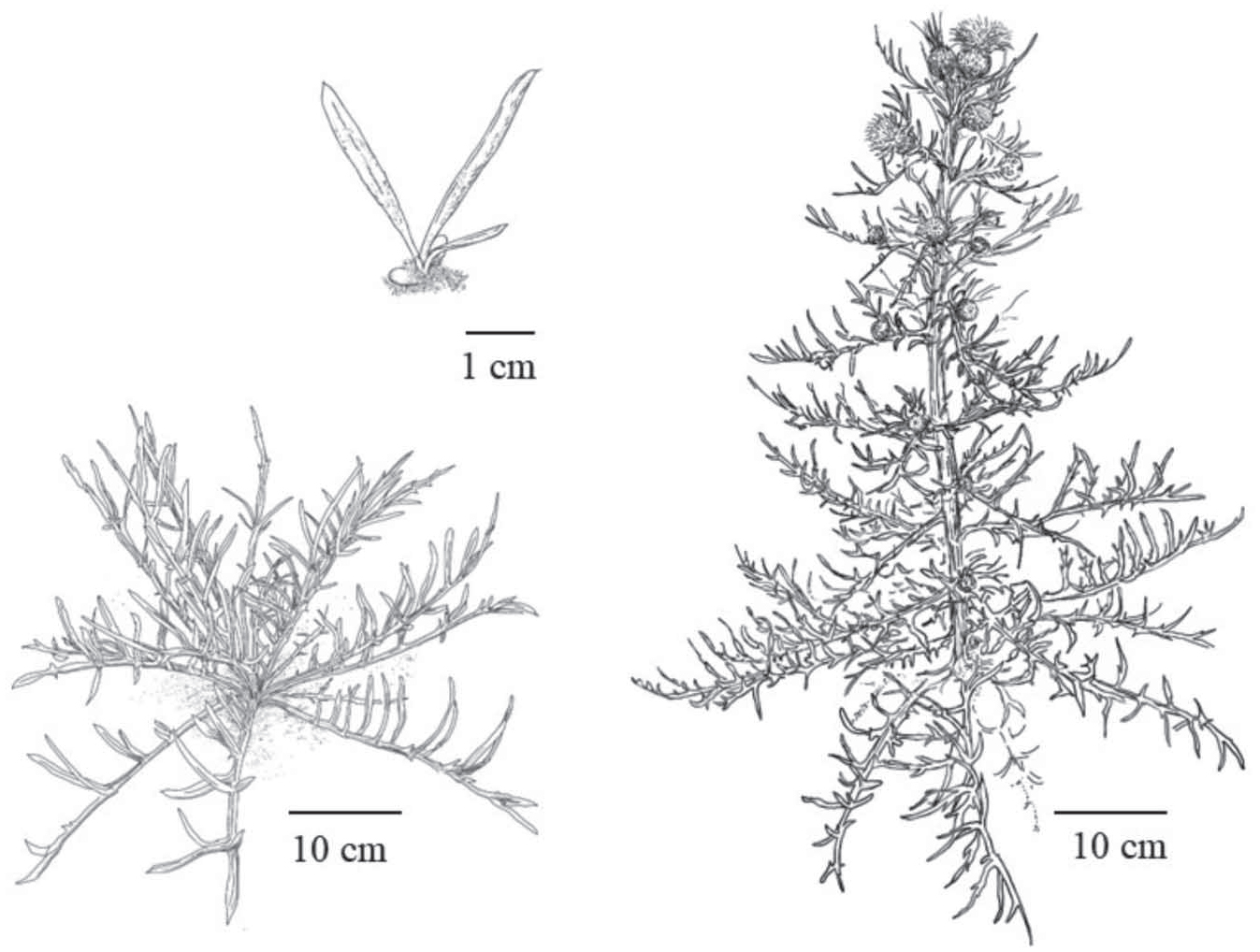
The subject of the present study, Cirsium pitcheri (Torr. ex Eaton) Torr. & A. Gray (Asteraceae), commonly known as Pitcher’s thistle, is a U.S.A. federally- listed threatened native plant, endemic to the dunes of the western Great Lakes shores, where it colonizes open sandy areas maintained by cyclic natural disturbance processes (Pavlovic et al. 2002). Optimal habitat includes both simple linear dunes consisting of a single ridge of sand between the lake and forest, as well as extensive perched dunes and blowouts extending hundreds of meters from the lake shore, such as at Sleeping Bear Dunes National Lakeshore on Lake Michigan. The species is emblematic of coastal dunes in Lake Michigan and Lake Huron, and plays an important role in the dune ecosystem. In particular, its relatively early flowering phenology may be critical for pollinator communities on the dunes (Jolls et al. 2019). Plants live for four to eight years as non-flowering vegetative rosettes, then flower once and die (Loveless 1984; McEachern 1992) (Figure 1).

FIGURE 1.

The three life stages of Cirsium pitcheri tracked in the demographic monitoring plot: (top left) seedling; (bottom left) large vegetative rosette; (right) flowering plant. Drawing by E. Binney Girdler.

Our study examines the effect spatial variation may have on the timing and size of flowering on Cirsium pitcheri within the dune system. Because of the dynamic nature of the dune environment and the strong elevation and disturbance gradient from the shoreline to the forest (Maun and Perumel 1999), plants living even a small distance apart can be exposed to quite different nutrient and water availability in addition to being affected much differently by climate-related factors (Lichter 1998, 2000). Using a long-term demographic data set, we explored spatial variation in age at flowering across a dune gradient and asked whether early-flowering plants were doing well or hedging their bets. We used size data to test two hypotheses: (1) the younger-flowering plants had ample resources, causing them to be able to reach a flowering threshold size more quickly, or (2) these plants grew slowly and thus had a higher likelihood of dying, resulting in early reproduction at a smaller size.

Materials and Methods

Demographic data have been collected annually from 2006 to 2022 in a 40 × 50 m plot located on the shores of Sturgeon Bay on Lake Michigan, Wilderness State Park, Emmet Co., Michigan, USA (45.72°, −84.94°). The plot was established by Dr. Claudia Jolls and her students and has served as the basis of many publications (Havens et al. 2012; Jolls et al. 2015) (Figure 2). One of us (EBG) took over sampling the plot starting in the summer of 2020 to continue the long-term demographic data collection; both LAP and EBG collected data during the summer of 2023 (although that year of data is not included in our analysis). The plot includes a gradient of elevation typical of linear dune systems in the Great Lakes and elsewhere including foredune (dune slopes facing the lake) and backdune (slopes facing inland). From 2006, the plot has been subdivided into 20 smaller 10 × 10 m areas to better keep track of plants in the field. For the current analysis, we divided the larger plot into five zones to capture the gradient of slope and elevation from the shoreline inland. Each zone is 10 m × 40 m oriented with the longer axis parallel to the lakeshore (Figure 2). The zones differ in aspect (Zones 1, 2, and 3 face west; Zones 4 and 5 face east), slope (Zones 3 and 4 are steepest), and vegetative cover (Zones 1 and 2 are more sparsely vegetated). The difference in elevation from the toe (front of Zone 1) to the top of the dune (boundary between Zones 3 and 4) is about three meters (Figure 2; see elevation profile inset). Ammophila breviligulata Fern. (Poaceae) (American beachgrass) dominates Zones 1 and 2. It is still prevalent on the dune ridge (Zones 3 and 4) and to a lesser extent on the back dune (Zone 5), co-occurring with patches of Asclepias syriaca L. (common milkweed), Salix spp. (Salicaceae) (willows), Juniperus communis L. (Cupressaceae) (juniper), Prunus pumila L. (Rosaceae) (sand cherry), and Arctostaphylos uva-ursi (L.) Spreng. (Ericaceae) (bear-berry).

FIGURE 2.

Location of the demographic monitoring plot at Wilderness State Park, Emmet County, Michigan (inset shows location within the Great Lakes region) indicated by the solid rectangle, divided into five zones, indicated by dashed lines. Each zone is 10m × 40m oriented with long axis parallel to the lakeshore. The elevation difference from the toe to the top of the dune is approximately three meters. Elevation of Lake Michigan in the 2019 Google Earth satellite image is approximately 177 m.

Demographic data analyzed here were collected annually in late June and early July from 2006 to 2022 in each zone. Individuals were followed through time by using numbered ID stamps on metal tags affixed to Cirsium pitcheri individuals by vinyl-coated wire. Plant size was measured as taproot diameter (mm) just below the crown (also called root crown diameter) on non-flowering C. pitcheri plants.

For the following analyses, we employed custom R scripts in RStudio (R Core Team 2023), utilizing in-house coding procedures tailored to our specific analytical requirements. For the flowering size and age analysis, we selected flowering plants from the 17-year dataset whose entire lifespan was known, i.e, plants first tagged as seedlings and followed until their flowering year, a total of 296 plants. Sample sizes in the Zones 1 through 5 are 23, 179, 33, 43, and 18 plants, respectively. For all models, the size variable, taproot diameter, was natural log- transformed.

Our measure of the fecundity of each plant was the number of capitula (flowering heads). We determined both the age at flowering and the size of vegetative plants the year before they flowered; plants were not measured after they had bolted, since taproot diameter tends to shrink when plants invest resources into the flowering stalk. To quantify the effect of size on the probability of flowering, we selected all instances of a vegetative plant in year t that survived to year t+1 (n = 951 transitions of 296 unique plants; a plant will be represented more than once since each has 2 to 12 transition years). We estimated the probability of flowering in year t+1 (a binary variable, 0 or 1) as a function of ln (taproot diameter in year t) (fixed effect) using a linear model fit by maximum likelihood with Laplace approximation and a binomial (logit) distribution using the lme4 package (Bates et al. 2015) in RStudio (R Core Team 2023). A mixed model with ‘zone’ as a random effect was not deemed a superior fit, as indicated by the Akaike Information Criterion (AIC). The AIC is a measure that balances model goodness-of-fit with complexity (Burnham and Anderson, 2002). In our context, AICfull represents the AIC for the full model with zone as a random effect, while AICreduced corresponds to the AIC for the reduced model, with no zone term. The difference (AICfull – AICreduced) was less than 2; in other words, the simpler model was more favorable, indicating a relatively better fit without sacrificing explanatory power. To determine the significance of this reduced model, we fit an even more reduced model with only an intercept term, and utilized a chi- square test to compare the deviance of those two models.

We then analyzed the spatial variation in flowering age (years) and natural log-transformed (ln) size in year t (taproot diameter, mm) using general linear models in R (R Core Team 2023) with zone (factor with 5 levels) as the explanatory variable, using Analysis of Variance to determine significance. Following the assessment of main effects through linear model ANOVAs, we conducted pairwise Tukey Honestly Significant Difference (HSD) tests to discern specific differences between zones.

We estimated the relative growth rate (RGR) as ln (taproot diameter at year t+1) – ln (taproot diameter at year t). We combined the yearly transitions between vegetative stages for all plants, resulting in a sample size of 914 data points representing growth from one year to the next for 291 unique plants (note: these were plants that did not flower in year t+1). To test for an expected relationship of RGR with size, we used a linear model of RGR as a function of ln (taproot diameter in year t). Similar to the flowering probability model described above, a simple model without a random zone effect had a relatively better fit (AICfull – AICreduced) < 2.

To test for the expected relationship between fecundity and size, we used a linear model of ln (number of flowering heads in year t+1) as a function of ln (taproot diameter in year t) as a fixed effect and location on the dune (zone) as a random effect using the lme4 package (Bates et al. 2015). In this case, (AICfull – AICreduced) > 2, so we retained the random “zone” effect in the model. For the fecundity model, we omitted four plants with > 25 flowering heads as outliers because they were likely the result of multi-stalked individuals, damaged when they were vegetative rosettes, resulting in a final sample size of 292 flowering plants.

Results

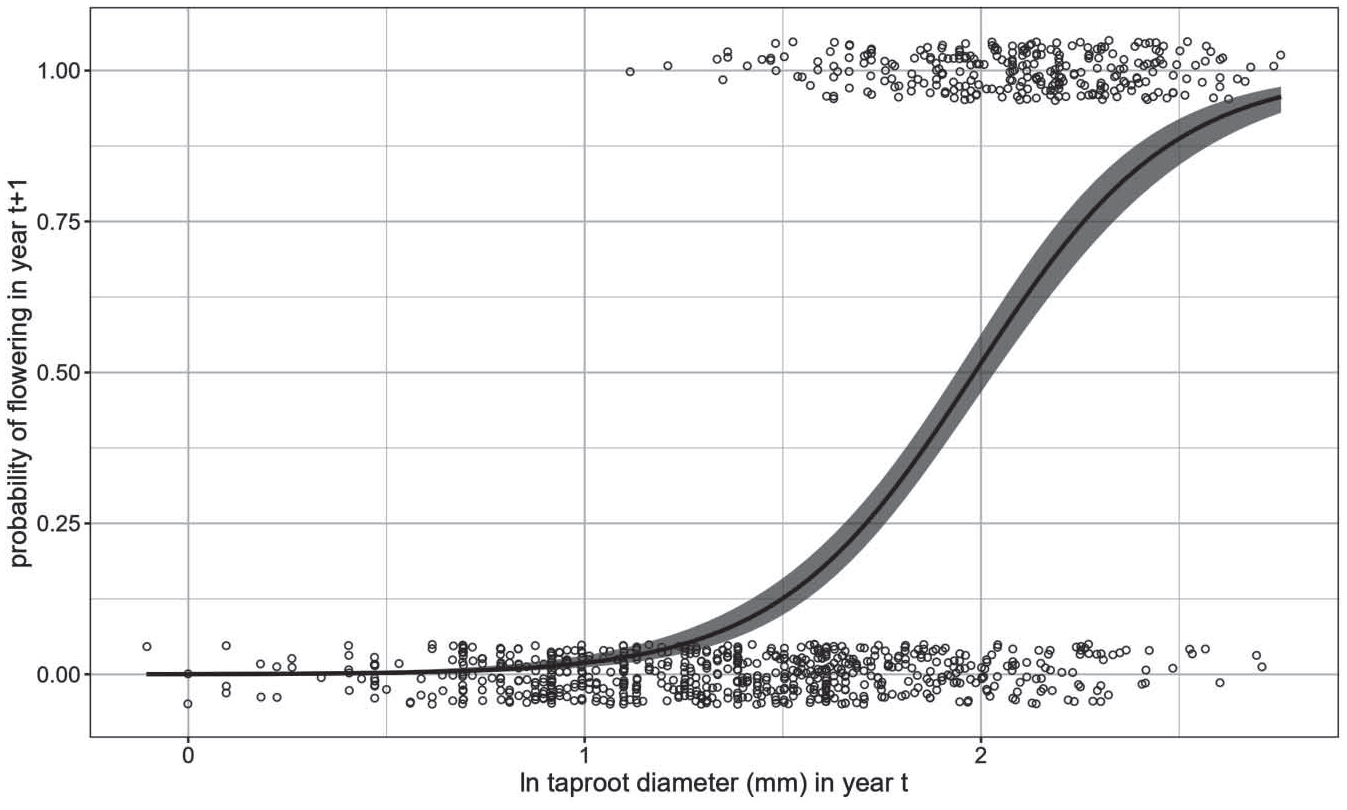
In the 17-year dataset, we found that the probability of Cirsium pitcheri flowering in year t+1 significantly depended on the size of a plant in year t (Figure 3). The logistic regression analysis revealed a significant association between the binary outcome variable (1=flowering, 0 = not) and the natural logarithm of taproot diameter in year t+1, as evidenced by a chi-square test (χ2 = 431.15, df = 1, p < 0.0001), indicating a substantial improvement in model fit compared to the model with just the intercept. In other words, larger plants were much more likely to flower compared to smaller plants.

FIGURE 3.

The probability of flowering in year t+1 depends on the size of a plant in year t. Shown is the fitted slope of the logistic regression model with a 95% confidence level interval (indicated by the shading surrounding the curve). Each circle is the fate of a single plant; a value of zero indicates the plant did not flower, a one indicates a plant did flower. Circles are jittered around these values to emphasize sample size (n = 951 plant transitions and 296 unique plants).

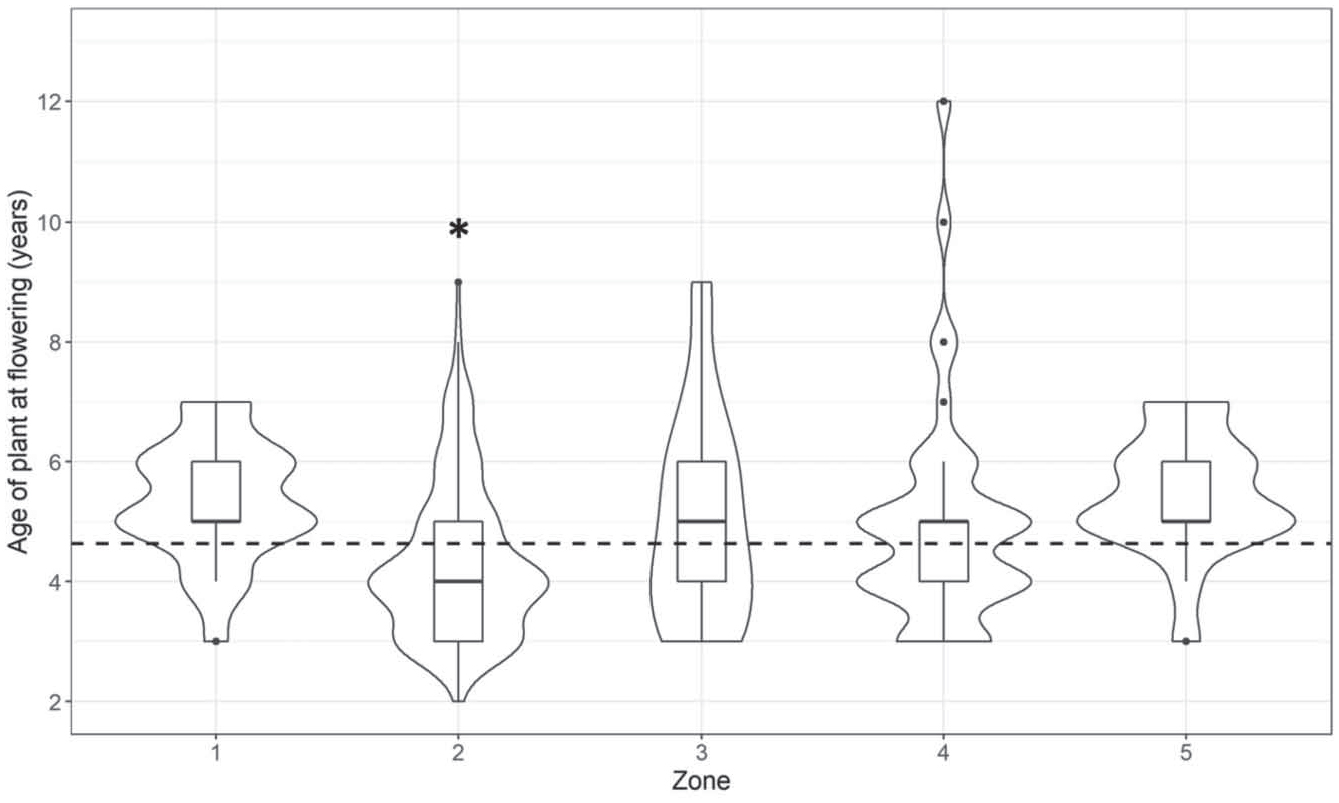
Overall, Cirsium pitcheri plants in our plot ranged in age at flowering from 2 years to 12 years, with a mean (±SD) of 4.6 (±1.45) years. We found spatial variation in the age of flowering plants (One-way ANOVA: F[4] = 6.508, p < 0.0001) (Figure 4). In particular, plants in Zone 2 flowered on average a full year earlier than plants in the other zones (4.3 years versus 5.3, 5.0, 4.9, and 5.5 years for Zones 1, 3, 4, and 5; Tukey’s HSD pairwise p-values: 0.008, 0.059, 0.060, 0.011, respectively) (Figure 4).

FIGURE 4.

The mean age at which plants flower differs by zone (One-way ANOVA: F[4]= 6.508, p < 0.0001). The widths of the violin plots represent the density or distribution of the data points at different values along the y-axis. A wider section indicates higher data density; more data points fall within that range. Interior box-and-whisker plots show median size as a thick line; the box shows the second and third quartiles, and the two whiskers show the first and fourth quartiles; solid dots indicate outliers. The overall mean age of all plants is shown by the horizontal dashed line. Tukey’s HSD test showed that plants in Zone 2 (*) flowered significantly earlier than plants in any of the other zones, which did not significantly differ from each other. Sample sizes in the order of zones are 23, 179, 33, 43, and 18 plants.

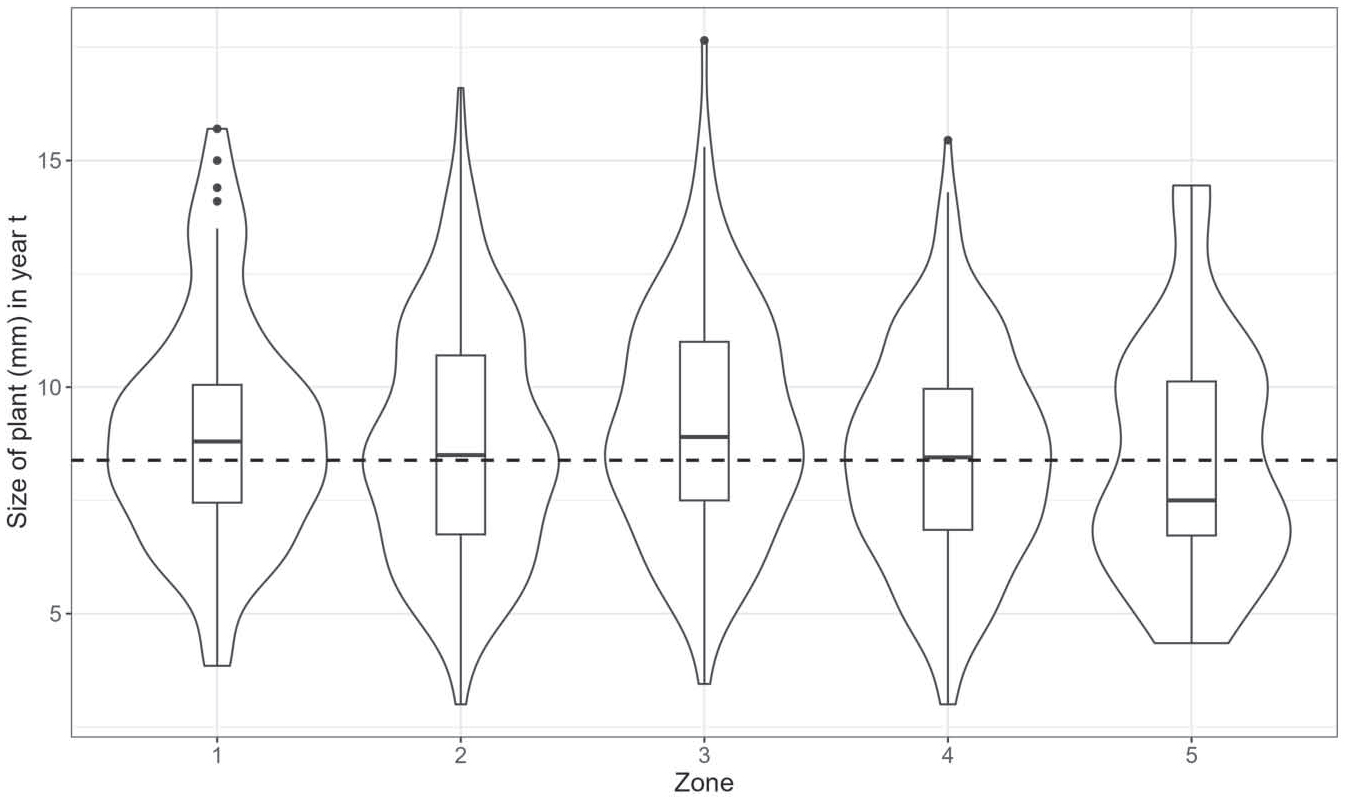
However, despite this spatial difference in flowering age, we found no significant differences by zone in the size of plants the year before they flowered (One-way ANOVA: F[4] = 2.148, p = 0.07) (Figure 5). Tukey’s HSD test showed no significant pairwise differences between zones (all pairs p > 0.3, except Zone 3 and 4, p = 0.069). In particular, plants in Zone 2, although flowering on average at four years of age, flowered at similar sizes compared to plants that grew an extra year. The mean (±SD) taproot diameter (untransformed) of all flowering plants the year before flowering was about 8.4 (±1.4) mm (Figure 5).

FIGURE 5.

The mean size in year t after which plants flower in year t+1 is similar in all zones on the dune (One-way ANOVA: F[4] = 2.148, p = 0.07). The widths of the violin plots represent the density or distribution of the data points at different values along the y-axis. A wider section indicates higher data density; more data points fall within that range. Interior box-and-whisker plots show median size as a thick line; the box shows the second and third quartiles, and the two whiskers show the first and fourth quartiles; solid dots indicate outliers. The overall mean size of all plants is shown by the horizontal dashed line. Sample sizes in the order of zones are 23, 179, 33, 43, and 18 plants.

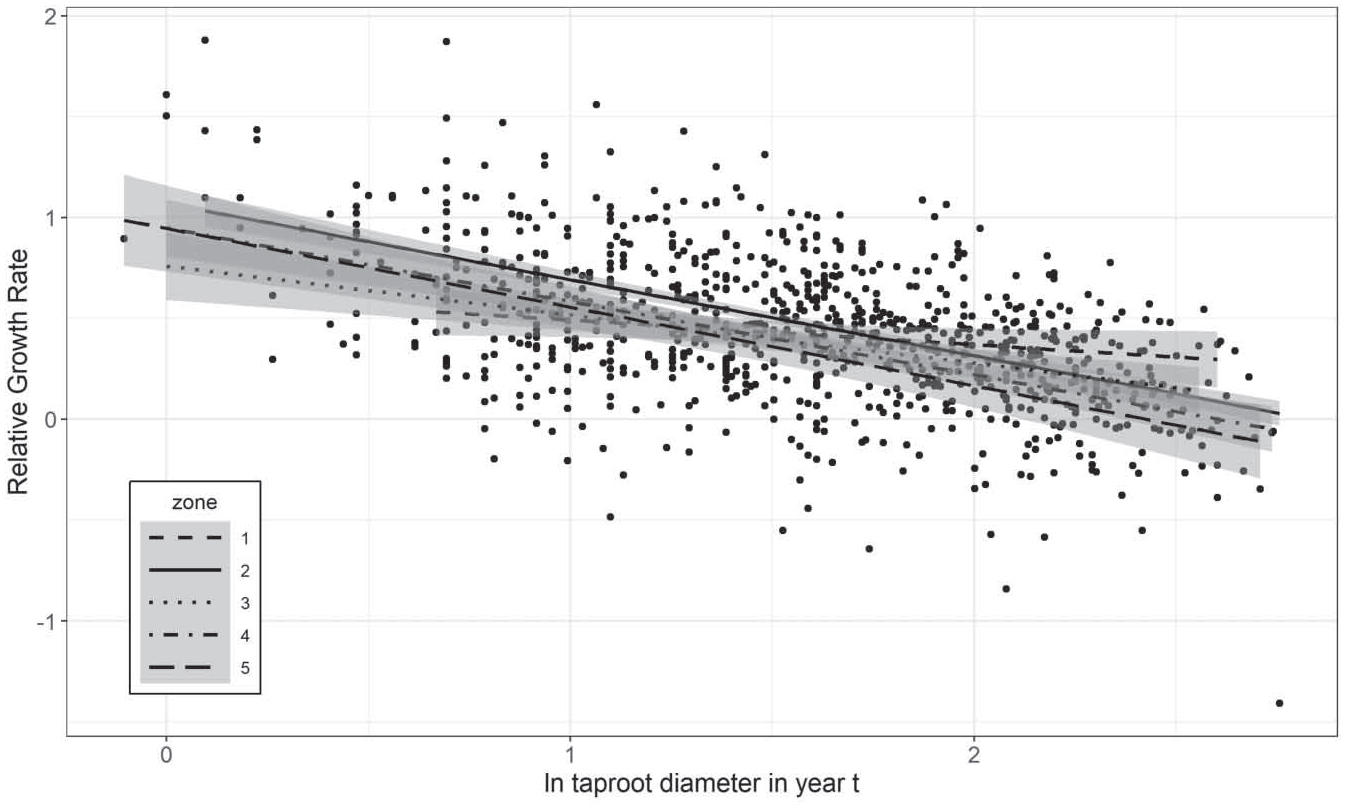
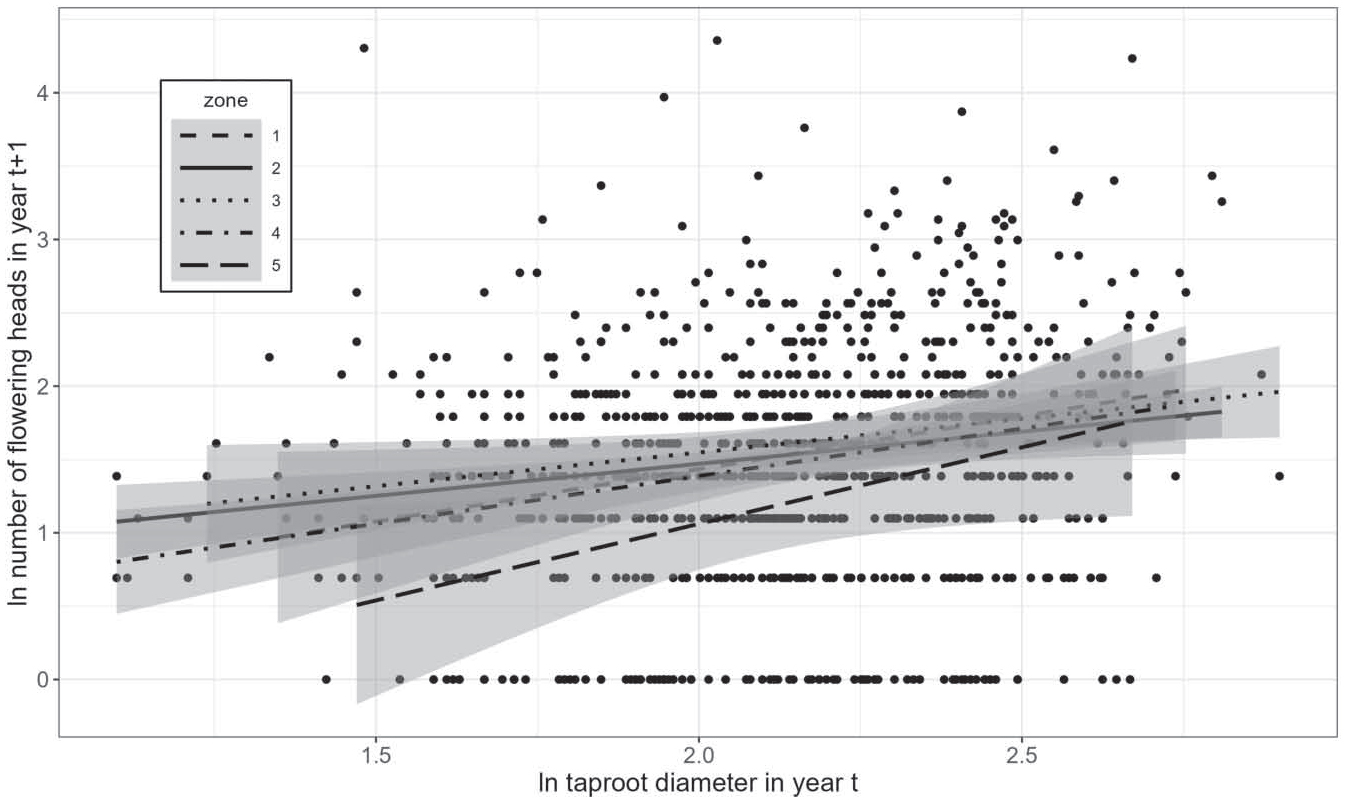
We found that the relative growth rate for Cirsium pitcheri at Wilderness State Park was a decreasing function of size in year t. The mean slope for the five zones is – 0.33, which is highly significant (p < 0.001, R2 = 0.27); the slopes do not differ by zone (Figure 6). Fecundity, estimated as the number of flowering heads in year t+1, increases with the size of the taproot in year t regardless of zone (F[1, 914]= 42.317, p < 0.001, Figure 7). Zone further explained variation in flowering heads (F[4, 914]=2.4967, p = 0.0414); plants in Zone 5 had significantly fewer flowering heads than plants in Zones 2 and 3 (Tukeys HSD, p < 0.05). No other pairwise comparisons were significantly different (Tukeys HSD test, p > 0.05).

FIGURE 6.

Scatter diagram showing the relationship between relative growth rate and the natural log of taproot diameter. Shown are fitted slopes for each zone and a 95% confidence level interval (indicated by the shading surrounding each curve) for linear model predictions, although slopes for zones did not significantly differ. Overall, size was a significant predictor of relative growth rate (p < 0.001, R2 = 0.27) The sample size is 296 plants, with 914 data points representing growth transitions between years.

FIGURE 7.

Scatter diagram showing the relationship between the number of flowering heads in year t+1 and taproot diameter in year t. Shown are fitted slopes for each zone and a 95% confidence level interval (indicated by the shading surrounding each curve) for linear model predictions. Zones had significantly different slopes (F[4, 914]=2.4967, p = 0.0414). Sample size is 292 plants (four outliers were omitted).

Discussion

Our findings provide support for the first of our alternate hypotheses: Cirsium pitcheri plants that flowered a whole year earlier than plants in other zones did so because they reached a threshold flowering size that appears typical of this species, at least at this site. Plants did not flower early as a conservative bet- hedging strategy to avoid the risk of death.

We therefore conclude that there is an optimum threshold size at which Cirsium pitcheri appears to flower, and that early-flowering plants did not hedge bets due to poor prospects, at least as indicated by slow growth. Although the literature on this threatened plant notes that the length of the juvenile stage ranges from four to eight years (Loveless 1984; Havens et al. 2012), we here report the first estimate of the flowering size threshold as 8.4 (±1.4) mm. Our long-term comprehensive data set also expands the range of the records for the vegetative juvenile stage for C. pitcheri (two to 12 years at Wilderness State Park).

Life history theory for monocarpic plants suggests that a law of diminishing returns applies: if fecundity increases with size but relative growth rate (RGR) decreases with size, the payoff of delayed reproduction gets smaller as the plant grows (Metcalf et al. 2003). Consistent with that expectation, we found that RGR in Cirsium pitcheri at our site was a decreasing function of size and that fecundity increased as plants grew larger. Like many other monocarpic perennials, selection has favored a threshold size that will instigate flowering in C. pitcheri. Despite within-site variation in age at flowering across the lake-to-forest dune gradient, the size of the plant the year before flowering was consistent. Whether this threshold size for flowering is common across the species’ range is unknown. There are several ongoing studies of C. pitcheri in the Great Lakes (McEachern et al. 1994; Havens et al. 2012; Rand et al. 2015; Halsey et al. 2016; Nantel et al. 2018); doubtless these authors have data to test for larger scale patterns in flowering age and size.

Future work could also explore whether the threshold size we have identified here (8.4 ± 1.4 mm) results in a theoretical maximum reproductive yield for Cirsium pitcheri. There are several methods to predict optimal threshold sizes that will maximize fecundity and fitness, such as integral projection models (Rees and Rose 2002; Williams 2009), and the evolutionarily stable strategy approach (Hesse et al. 2008). Additionally, future studies might investigate how the survivorship of C. pitcheri varies with increasing size, particularly how the survival of plants tracks beyond the identified threshold flowering size. Such investigations will inform estimates of generation time, population growth rate, and the likelihood of population persistence in this threatened species.

We conclude that for the Wilderness State Park population, our Zone 2, which encompassed not the newest beach but the first rise of the foredune, comprises a microenvironment where Cirsium pitcheri plants grew rapidly and flowered at younger ages and, as such, may represent optimal habitat. This foredune habitat may represent a within-site source population, with the other zones being sinks. Such insight into the spatial demographic patterns of C. pitcheri informs the conservation and recovery planning of this threatened species; maintenance of the foredune throughout this threatened species’ range may be important to its persistence. Future work should more closely examine C. pitcheri vital rates across the dune gradient to determine what environmental factors contribute to variation in success. Paradoxically, it might be active sand movement and burial that stimulates growth (Maun and Perumal 1999). In contrast, such active sand movement might bury competitors and release C. pitcheri from competition.

Finally, we note that over the course of this 17-year study, the elevation of Lake Michigan has changed dramatically, with a historic high level of 177.45 m in June 2020 and a low of 175.57 m in January of 2013 (GLISA, 2023), a change of almost two meters. The Great Lakes have fluctuated historically in response to climate, especially to the evaporation-precipitation ratio (McEachern 1992; Gronewald et al. 2013). These coastal processes can greatly affect dune geomorphology. The foredune environment we have identified as optimal habitat for Cirsium pitcheri might be at risk of erosion during periods of high lake levels or at risk of excessive sand burial during the period just after high lake levels when exposed sand is blown inland. Indeed, we have seen both processes at Wilderness State Park and other locations from 2019 to 2023. Precipitation and lake levels are projected to increase in response to human-induced climate change. Kayastha et al. (2022) predict that Lake Michigan will experience an average annual increase in water level of 0.44 m above the 2020 high by 2040–2049.

We note, however, that C. pitcheri occurs not only on simple linear dunes like our demography plot, but also in discontinuous patches of open sand (blowouts), continuous dune fields, and perched dune systems in the Great Lakes (Loveless 1984; Pavlovic et al. 2002). A range-wide comparison of C. pitcheri demography among the various populations in these different habitats will be important to understanding the threats to its long-term persistence and to assessing whether a habitat analogous to our Zone 2 is critical to C. pitcheri population viability. It is critical to continue close study of C. pitcheri and other dune endemic species and to consider the possibility of management interventions such as assisted dispersal and reintroductions to ameliorate effects of climate change on this sensitive ecosystem.

Author Contributions

EBG conceived of this study, LAP and EBG collected the demographic data (along with previous researchers, see acknowledgments). EBG and LAP jointly designed and conducted the analyses and created the figures. LAP drafted the manuscript, and both authors edited and revised the manuscript.