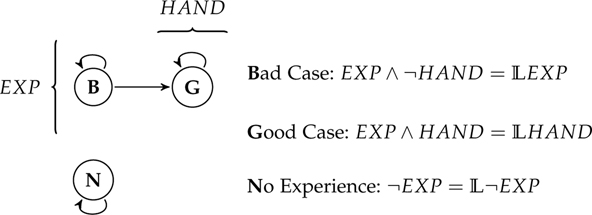Just As Planned: Bayesianism, Externalism, and Plan Coherence

3.1 Externalism

The externalist about rationality thinks that rational uncertainty about what’s rational for one to believe is as possible as rational uncertainty about everyday empirical matters, such as the weather or the outcome of a game. This paper focuses on a specific source of uncertainty about rationality — uncertainty about what one’s evidence is. Thus restricted, the externalist thinks that there are possible experiments where one could learn evidence that would leave one rationally uncertain of what one’s evidence is. More precisely:

externalism (formal) There are possible experiments where the agent can learn some evidence E_i such that .⁵

Our question is not whether externalism is true, but whether the standard Bayesian strategies for justifying update rules can be reconciled with it.

3.2 Evidential Opacity

As is common in Bayesian epistemology, we are treating the agent’s evidence as exogenous to the model. We can give it a functional characterization: their evidence is the strongest proposition that their experiences in the experiment enable them to take for granted in their reasoning. But we have not said, and will not say, anything about what it takes for a proposition to have this status. However, externalists typically hold their view in part because they deny a strong, but natural, assumption about evidence. To state it, we’ll need the following definition:

Transparent/Opaque Evidence (definition): E is transparent if the agent is certain in advance that they will learn that E just in case E is true, i.e. if $C(E\leftrightarrow \mathbb{L}E)=1$.⁶ If E is not transparent, we say that it is opaque.

In practice, when discussing opaque evidence, we’ll consider only cases where the agent is uncertain whether they will learn some proposition if it is true (i.e. ), not cases where the agent is uncertain whether some proposition is true if they will learn it (i.e. ). In this paper, I remain neutral on the possibility of the latter kind of case, and nothing that I say precludes its possibility.

Now, philosophers who accept externalism typically do so because they deny that evidence always has to be opaque. That is, they typically deny:

evidential transparency In every possible experiment, every potential body of evidence is transparent.

Intuitively, there is a direct connection between externalism and evidential transparency: if you can only ever learn transparent evidence, then your evidence will always tell you what your evidence is, so that it would seem irrational to be uncertain of what it is. If, on the other hand, you can have opaque evidence of the kind that leaves open what your evidence is, the right response would seem to be uncertainty about your evidence.

To better understand evidential transparency, and why one might deny it, consider one of the externalist’s favourite cases — a sceptical scenario:⁷

Here’s a Hand: You’re about to open your eyes, and know that you will either have an experience as of a hand (EXP) or not. You know that, if you don’t have the hand-experience, then you don’t have a hand. However, if you do have the hand-experience, you may in fact have a hand (HAND), or it could be that you’re being deceived by a malicious demon, and there is no hand (¬HAND).

According to the standard externalist treatment of sceptical scenarios your evidential situation is as follows: if you veridically experience the hand — call this the Good Case — you will learn that you have a hand, i.e. that you’re in the Good Case. On the other hand, if you’re deceived by the demon — call this the Bad Case — you will not learn that you have a hand, but merely that you have an experience as of a hand (Williamson, 2000, ch. 8). What evidence you have is thus determined by facts that are external to you. An externalist may think this for different reasons, but in Williamson’s case, this is because he thinks that your evidence is what you come to know by looking, which itself depends on whether there is in fact a hand in front of you.

The externalist description of the case is represented in Figure 1. Each circle represents a world that is possible for all you know before looking. The arrows represent the possible evidential facts after looking — an arrow goes from one world to another iff your evidence in the former world (after looking) doesn’t rule out you being in the latter world. Thus, according to the externalist, in the Bad Case your evidence only rules out you not having had a hand-experience (¬EXP), whereas in the Good Case, your evidence does rule out you having had a misleading experience as well (EXP ∧ ¬HAND).

Figure 1:

The Externalist Description of Here’s a Hand.

The point of the example is that if this really is the evidential structure of the experiment, then your evidence in the Bad Case is opaque. That is because your evidence in the Bad Case (EXP) doesn’t rule out the possibility that you’re in the Good Case, where your evidence is different: that you had the experience and that you have a hand. So your evidence in the Bad Case is not equivalent to the claim that it is your evidence ($\mathbb{L}EXP$), since it doesn’t entail it. If the externalist is right about sceptical scenarios, evidential transparency is false.

4.1 Planning

4.2 Which Plans Trigger Rational Requirements?

We want to argue for conditionalization by showing that the plan to conditionalize is the best plan, and that, since one ought to “stick to the plan” after learning, one should conditionalize. Any such argument faces a problem, however: the plan to conditionalize is not best if we compare it to all other plans. The standard example is the omniscience plan, which says, for every world w, to assign credence one to all truths and credence zero to all falsehoods at w (Greaves & Wallace, 2006, p. 612). On natural ways of evaluating plans, this is the best plan there is, since it will make the agent’s beliefs both as accurate (as close to the truth) as can be, and as good a guide to action as one could ask for, since one can never lose by betting on the truth and only on the truth. And yet there is no rational requirement to be omniscient. So even though the omniscience plan is the best plan, there is no requirement to implement it after learning. As I’ll put it, one is not required to be plan coherent with respect to it.

It should be clear that the problem with the omniscience plan is that it doesn’t have the right conditions: by assigning different credence functions to every world, it makes distinctions that are too fine-grained for there to be a requirement to implement it after learning. To exclude such plans from consideration, we’ll say that they are not admissible in the following sense:

Admissibility/Plan Coherence (definition): A plan is admissible if its condition is such that, after learning, a rational agent will implement the antecedently best actionable plan with that condition. We’ll say that the agent is required to be plan coherent with respect to the admissible plans.

Since we’ll want to conduct our discussion both in terms of conditional and unconditional plans, I’ll think of admissibility as a property of conditional plans in the first instance, and will say that an unconditional plan is admissible iff all of its elements are admissible.

Which plans are admissible? There are two natural answers to this question. On the first, one is not required to implement a plan when one has not learned its condition. In particular, if I have not learnt that w is actual, I am not required to implement the best plan for w, even though w is in fact actual. I am only required to implement the plan for the condition that I have learnt, i.e. the best plan for my evidence E. This gives us:

epistemic admissibility If the agent learns that E, the admissible plans are those with E as their condition, so that after learning that E, a rational agent will implement the antecedently best actionable plan for what to do or believe if E is true.¹⁴

The second answer is that we can exclude the omniscience plan because it is not a plan for what to believe given what one learns. That is, its conditions aren’t propositions about what one has learnt ($\mathbb{L}E$ for some E), but cut across such propositions. In other words, there may be two worlds w₁ and w₂ such that the agent has learnt the same thing at those worlds, but where the omniscience plan recommends different beliefs. We can exclude such plans by assuming:

auto-epistemic (a-e) admissibility If the agent learns that E, the admissible plans are those with $\mathbb{L}E$ as their condition, so that after learning that E, a rational agent will implement the antecedently best actionable plan for what to do or believe if $\mathbb{L}E$ is true (i.e. if they learn that E).

The distinction between these two principles is easily overlooked, because they are equivalent in experiments with only transparent evidence. If any E that the agent may learn is transparent, then any such E is equivalent to $\mathbb{L}E$. Thus, the best plan for what to believe given E is just the best plan for what to believe given $\mathbb{L}E$.

What the standard arguments do is to focus on plans with E₁, E₂, … (or equivalently, $\mathbb{L}{E}_1$, $\mathbb{L}{E}_2$, …) as their condition, and prove that the plan to conditionalize is best among them. They can thus be understood as adopting one of these two accounts of admissibility, though this is not explicit in the presentation, because the attention is on identifying the best plan, not on what follows from the fact that it is best. That is, the standard arguments show:

plan conditionalization In any experiment with only transparent evidence, before learning, the plan to conditionalize on one’s evidence is the best unconditional plan with $\mathbb{L}{E}_1$, $\mathbb{L}{E}_2$, … (or equivalently, E₁, E₂, …) as its conditions. That is, PCond ≻ $\mathcal{P}$ for any other doxastic unconditional plan $\mathcal{P}$ with the same conditions.

This premise doesn’t entail conditionalization on its own. Just because the plan to conditionalize on one’s evidence was best before learning, it doesn’t follow that later, after acquiring more evidence, one should implement it. We need something to bridge the gap between prior plans and posterior implementation. That is the job of the principles of admissibility we have just reviewed. Helping ourselves to one of these two principles (it doesn’t matter which), we can now reason as follows: the best conditional plan for what to believe given E or $\mathbb{L}E$ must be to conditionalize on E, since, as plan conditionalization says, the best unconditional plan with $\mathbb{L}{E}_1$, $\mathbb{L}{E}_2$, … (or equivalently, E₁, E₂, …) as its conditions says to conditionalize on E if they learn that E (or equivalently, if E is true).¹⁵ Now applying either epistemic admissibility or a-e admissibility, it follows that upon learning that E, a rational agent will conditionalize on E, which is just what conditionalization says.

4.3 Two Arguments for Plan Conditionalization

Having seen how to argue from plan conditionalization to conditionalization, we will now look at two arguments for the former principle.

6.1 Which Plans Are Admissible?

How can the externalist respond? They could reject the accuracy framework, and the idea that dutch-bookability indicates irrationality. My suggestion, however, is to reconsider something that they have in common: the assumption about plan coherence (a-e admissibility) that has to be made in order to go from plan a-e conditionalization to a-e conditionalization itself. In particular, I think that externalists have good reason to reject a-e admissibility in favour of epistemic admissibility. That is, the conditions of the admissible plans are what you’ve learnt, not that you’ve learnt it. Since a-e admissibility is a premise in the arguments for a-e conditionalization, this allows externalists to reject those arguments as unsound.

To see why, let us think about practical planning for a moment. Imagine that our agent is now playing poker. Before the next card is drawn, they rightly conclude that, if they have a better hand than their opponents, the plan to raise the bet is best. The card is revealed, and as a matter of fact they do now have the best hand. However, since they cannot see their opponents’ hands, they don’t know this. In fact, given what the agent knows about the cards on the table and their opponents’ behaviour, it now looks like they have a worse hand than some of their opponents. In this situation, they are obviously not required to raise the bet, despite the fact that the best plan says to do so. The natural explanation, I suggest, is that they have not learnt that they have the best hand, and so are not required to implement the best plan for that condition. This is precisely the explanation offered by epistemic admissibility, according to which a requirement to implement the best plan in a class only takes effect when one has learned the condition of those plans.

Now returning to the epistemic case, in Here’s a Hand, this explanation shows where a-e admissibility goes wrong. In the Bad Case, while you have learnt EXP, you have not learnt $\mathbb{L}EXP$. Thus, the same objection as in the poker case applies: you have not learnt the condition of the best $\mathbb{L}EXP$-plan, and so aren’t required to implement it. To put the point differently: everyone will acknowledge that if we count one’s “situation” as what hand one has in a poker game, one should not always prefer what the better plan for one’s situation says. My suggestion is that this is because everyone agrees that one can have the best hand in a poker game, without having learnt this. But if we think of one’s “situation” as a description of what one’s evidence is, it has proved more tempting to think that one is required to prefer what the better plan for one’s situation says. However, if opaque evidence is possible, the same objection applies here: one can learn that E, without having learnt that one learnt that E.²¹

This argument against a-e admissibility from epistemic admissibility can be put on theoretically firmer footing by showing that the latter follows from two plausible principles of practical reasoning. First we have a diachronic principle:

irrelevance If what a rational agent learns doesn’t rule out any p-worlds, their preferences between plans with p as their condition will remain unchanged.

The idea is that if the agent doesn’t learn anything that rules out p-worlds, the new evidence doesn’t put them in a position to reconsider their plans for p, since they have not learnt anything about what could happen if p is true. The second premise concerns the agent’s practical reasoning after learning:

implementation If, after learning, a rational agent prefers ⟨p, ϕ⟩ to all other actionable plans with p as their condition, and if their evidence entails that p, then they will ϕ.

This is a synchronic principle of practical rationality, akin to that of means-end reasoning. We can think of it as saying that one can reason from one’s evidence and one’s preferences between conditional plans to a decision to implement the preferred plan. For example, if my best plan for rain is to bring a rain coat rather than an umbrella, and my evidence entails that it is raining, then I can decide to bring the rain coat on the basis of those two attitudes.

epistemic admissibility follows from these two premises. First, by learning that E, a rational agent doesn’t learn anything that rules out any E-worlds. Hence, their preferences between E-plans will remain unchanged, so that they still prefer the antecedently best E-plan to other E-plans. Second, if the agent learns that E, they have learnt something that entails that E, so that they will implement the best actionable E-plan, which as just shown is the antecedently best actionable E-plan.

Importantly, there is no parallel argument for a-e admissibility. Consider the best $\mathbb{L}E$-plan. To establish a-e admissibility, we would want to reason in two steps, as before: first that the agent’s preferences between $\mathbb{L}E$-plan will stay the same upon learning that E, and second that the agent will implement the best $\mathbb{L}E$-plan after learning. For the sake of argument, I am happy to grant the first step, since it follows from irrelevance on the assumption that the agent will only learn E if it is true.²² On this assumption, learning that E cannot rule out any $\mathbb{L}E$-worlds, since they are also E-worlds, so that irrelevance says that the agent’s preferences between $\mathbb{L}E$-plans will remain the same upon learning that E.

However, we would then have to show that the agent should implement the best $\mathbb{L}E$-plan after learning. In cases of opaque evidence, this doesn’t follow from implementation: in the Bad Case, the agent doesn’t learn anything that entails $\mathbb{L}EXP$ by learning that EXP, and so it doesn’t follow that they are required to implement the best plan for this condition. In other words, if the agent’s evidence is opaque, they cannot necessarily reason “I have learnt that E, and the best plan for learning that E is to ϕ, so I’ll ϕ”, because they have not learnt that they have learnt that E, and so cannot use $\mathbb{L}E$ in their deliberation. This is just an instance of the general fact that rational requirements are triggered not by just any facts, but by learnt facts. For example, if I know that if p, then q, this doesn’t commit me to believing that q unless I also know (or learn) that p. Similarly, the fact that I prefer the plan to ϕ to the plan to ψ given some condition doesn’t trigger a rational requirement to prefer ϕ to ψ unless I have learnt the condition.

Finally, recall that we introduced the admissibility principles to exclude plans such as the omniscience plan. Arguably, however, the stated motivations for excluding this and similar plans speak against a-e admissibility in cases of opaque evidence. First, Greaves & Wallace say that plans such as the omniscience plan require the agent to “respond to information that he does not have” (Greaves & Wallace, 2006, p. 612). I think that this problem is sometimes also shared by $\mathbb{L}E$-plans: requiring the agent to auto-epistemically conditionalize in the Bad Case is precisely to require them to “respond to information which he does not have” — namely the information that they are in the Bad Case. Even more revealing is Kenny Easwaran’s (2013, pp. 124–125) motivation for excluding the omniscience plan: that a plan should assign the same credence function to two states if the agent “does not learn anything to distinguish them”. Again, this problem is shared by $\mathbb{L}E$-plans when evidence is opaque: in the Bad Case the agent doesn’t learn anything to distinguish the Good Case from the Bad Case, and so should not be required to act on the plan to conditionalize on being in the Bad Case if they are in the Bad Case.

6.2 Is My Argument Unexternalist?

One may worry that, while the case against a-e admissibility seems reasonable, it clashes with a fundamental externalist principle: that facts about rationality can fail to be known to the agent. Doesn’t my complaint that one is not required to implement a plan if one doesn’t know its condition contradict this principle? This would be a serious problem if true, since my aim is to render Bayesianism consistent with externalism.

In reply, it is important to distinguish between rules and plans. The former are principles of rationality, and the objection is right that an externalist wouldn’t want to say that such a principle only applies when the agent knows what it says to do. My objection, however, is about the plan. A plan is a commitment of the agent, like a belief or an intention.²³ What I have claimed is that this commitment only generates the additional commitment to implementing the plan when the agent has learnt its condition.

This is perfectly in line with what externalists think. No externalist would say that any fact can be rationally used in one’s reasoning just by virtue of being true. To return to the above example, no externalist would hold the absurd view that if one knows if p then q, and p is true but not known or believed to be, one can rationally use p in one’s reasoning and is thereby rationally committed to believing that q. Rather, they think that one must stand in some substantive epistemic relation to p, such as knowing it or being in a position to know it, in order for such a requirement to be triggered. Or to take a practical example, my intention or desire to drink gin doesn’t rationally require me to intend or desire to drink the contents of the glass just because it happens to contain gin. A requirement is only triggered if I know that the glass contains gin, even for an externalist. That’s why many externalists think of one’s evidence as well as one’s practical reasons as consisting of the propositions that one knows, or stands in similar relations to, such as what one non-inferentially knows or is in a position to know (Littlejohn, 2011; Lord, 2018; Williamson, 2000). In the Bayesian framework, we call this relation “learning” or “having the proposition as evidence”.

The effects of the externalist principle that requirements of rationality can fail to be known are felt on another level. One source of uncertainty about rationality is that that one can stand in the right epistemic relation to a proposition without standing in the right relation to the higher-order proposition that says that one stands in the right relation to that proposition. So, for example, one can know if p then q and also know p, but fail to know that one knows that p. In such a case, the externalist would say that one is required to believe that q, even though one is not in a position to know that this is required. Similarly, an externalist about evidence would say that one can sometimes learn some E without learning $\mathbb{L}E$. It would then follow from epistemic admissibility that one is required to implement the best plan for E even though one doesn’t know that one is so required.

7.1 Why Plan Coherence?

I have argued that we should reject a-e admissibility in favour of epistemic admissibility. This suggests the following strategy: to argue for an update rule, we should consider plans with the evidence rather than a description of the evidence as their condition. In particular, if we could show that the plan to adopt C(·|E) is the best E-plan, epistemic admissibility would then kick in and require the agent to adopt the conditionalized credences. This is the line that I will pursue in the rest of this paper.

Before I do so, I want to address a more general challenge: I have argued that epistemic admissibility is a more plausible expression of the idea that rationality requires one to “stick to the plan” than a-e admissibility. But why think that rationality requires plan coherence of any kind? That is, why think that there are any admissible plans at all? I have already argued that if one did not learn the condition of the best plan, one need not be required to implement it. One can also have learnt too much to be required to implement it, as in a case where I have planned to sell my lottery ticket if I am offered $100 for it, but then learn that I am offered this amount and that it is the winning ticket. Here I have learnt more than the condition of the plan, which puts me in a position to rationally re-evaluate it.

What is plausible is that one should stick to a plan if one has learnt just enough, i.e. if one has learnt exactly the condition of the plan, no more and no less. Admittedly, I don’t have an argument against general scepticism about plan coherence,²⁴ though in this respect I am not in a worse position than those who appeal to a-e admissibility. To the sceptic, all I can offer is the intuitive plausibility of the claim that one should stick to the plan when none of the above objections apply. This is best brought out by considering how someone would justify their violation of the principle:

• A: Why did you bring your umbrella? I thought you said yesterday that wearing a rain coat was the better plan for rain.

• B: It was, yes. But then I learnt something that made me reconsider. Yesterday night I didn’t know that it was going to rain, so bringing the rain coat was the better plan for rain. But this morning, I learnt that it was raining, and in the light of that new information I decided to bring the umbrella instead.

• A: Wait, how can the fact that it is raining make you revise your plan about what to do if it rains?

A’s reaction seems justified. Either B was wrong about the plan to begin with, or they were wrong to revise it. That something happened cannot itself be a reason to reconsider what to do if it happens.

7.2 Conditional Plan Evaluation

In order to develop an argument for conditionalization based on epistemic admissibility, an adjustment will be necessary. The original arguments, which are restricted to experiments with only transparent evidence, establish conditionalization by showing that the best conditional plan for learning that E (i.e. for $\mathbb{L}E$) is to conditionalize on E. This claim was in turn justified by arguing that the best unconditional plan with $\mathbb{L}{E}_1,\mathbb{L}{E}_2$, … as its conditions was the plan to conditionalize on E₁ if the agent learns that E₁, conditionalize on E₂ if they learn that E₂, etc.

Since we intend to use plans with E₁, E₂, … as their conditions in a setting with opaque evidence, this kind of justification is not available, however. One can only form an unconditional plan from conditional plans if their conditions form a partition, but E₁, E₂, … is not guaranteed to form a partition in experiments with opaque evidence. For example, in Here’s a Hand, one proposition that you might learn is EXP, and another is EXP ∧ HAND. These propositions are consistent, and thus a plan to believe one thing given EXP and another given EXP ∧ HAND is not a real unconditional plan. However, as I will show, there is a similar way of evaluating conditional plans that escapes this problem. To this end, I will assume three principles about rational preference between conditional plans, and show that, combined with the claim that one ought to maximize expected utility, they pin down a unique way of evaluating conditional plans.

First, it is highly plausible that the preference relation between conditional plans satisfies some very minimal structural properties — that it is reflexive, and that two conditional plans with the same condition can always be compared:

reflexivity For any conditional plan A, A ⪰ A.

conditional completeness For any condition p and acts ϕ, ψ, either ⟨p, ϕ⟩ ⪰ ⟨p, ψ⟩ or ⟨p, ψ⟩ ⪰ ⟨p, ϕ⟩ (or both).²⁵

The third principle will do the heavy lifting, and is a version of Leonard Savage’s (1954) Sure-Thing Principle.²⁶ The idea is that if you have some partition of logical space, and for each cell of the partition prefer some act to another, you should be able to combine those preferences between conditional plans to form a preference between the unconditional plans that they make up. For example, suppose that it is better to bring an umbrella than a rain coat if it rains, and better to bring sunglasses than a cap if it doesn’t rain. If so, the unconditional plan to bring an umbrella if it rains and sunglasses if it doesn’t must be better than the plan to bring a rain coat if it rains and a cap if it doesn’t. Formally:

conditional dominance For any acts ϕ₁, …, ϕ_n, ψ₁, …, ψ_n, and any partition p₁, …, p_n, if for all i (1 ≤ i ≤ n),

$\langle p_i,{\varphi }_i\rangle \succcurlyeq \langle p_i,{\psi }_i\rangle$

then

$\left\{\langle p_i,{\varphi }_i\rangle \mid 1\le i\le n\right\}\succcurlyeq \left\{\langle p_i,{\psi }_i\rangle \mid 1\le i\le n\right\}.$

These assumptions, combined with the idea that we evaluate unconditional plans by their expected value, suffice to establish the following claim:

conditional expectation lemma Given conditional dominance and reflexivity, and if preferences between unconditional plans are determined by their expected value, then for any acts ϕ, ψ (whether doxastic or practical), and any proposition E, if C(·|E) is defined and

$\langle E,\varphi \rangle \succcurlyeq \langle E,\psi \rangle$

then

$E{V}_{C(\cdot \mid E)}\varphi \ge E{V}_{C(\cdot \mid E)}\psi$

where EV_cA is the expected value of act A according to credence function c.

The proof is in the Appendix. We have thus arrived at a way of evaluating conditional plans: rational preferences between plans with some condition reflect their conditional expected value.

8.1 A New Accuracy Argument

I begin with the accuracy-theoretic argument, which builds on Greaves & Wallace’s Accuracy Argument, but which is now stated in terms of the best conditional doxastic plan for the agent’s evidence. Just as before, it proceeds in two steps. First, it is shown that the conditional plan to conditionalize on E is the best plan for E:

conditional plan conditionalization For any possible evidence E, the best plan for E is to conditionalize on E. That is, for any credence function $c^{*}\ne C(\cdot \mid E),\langle E,C(\cdot \mid E)\rangle \succ \langle E,c^{*}\rangle$.²⁷

Justification: Assume, for reductio, that there is some credence function c^* ≠ C(·|E) such that it is not the case that $\langle E,C(\cdot \mid E)\rangle \succ \langle E,c^{*}\rangle$. By conditional completeness, it follows that $\langle E,c^{*}\rangle \succcurlyeq \langle E,C(\cdot \mid E)\rangle$. Now applying the conditional expectation lemma, we get EV_C(·|E)c^* ≥ EV_C(·|E)C(·|E). Assuming that the value of a credence function is its accuracy, it follows that C(·|E) regards c^* as at least as accurate as itself in expectation. But that is impossible, since by Strict Propriety any probability function regards itself as more accurate in expectation than any other credence function, and C(·|E) is a probability function, since C is. Hence the assumption must have been false: ⟨E, C(·|E)⟩ is the best doxastic conditional plan with E as a condition.

Note that this principle is about the best plan for E, not the best plan for $\mathbb{L}E$. We can thus argue as follows: Suppose that our rational agent learns that E. Assuming that all doxastic plans are actionable (i.e. that the agent can adopt any credence function upon learning that E), it follows from conditional plan conditionalization that the best actionable E-plan is to conditionalize on E. Thus, by epistemic admissibility the agent will conditionalize on E. Hence, conditionalization is true. Since no assumptions have been made about the relationship between E and $\mathbb{L}E$, this conclusion holds irrespective of whether E is transparent or opaque.

8.2 A Practical Argument

The conditional expectation lemma also suggests a different argument for conditionalization, one that doesn’t employ the accuracy framework. In fact, we can dispense with the idea of doxastic planning altogether. As long as practical planning — planning what to do, rather than what to believe — obeys the assumptions listed in the conditional expectation lemma, we can establish conditionalization by combining epistemic admissibility with expected utility reasoning.²⁸

Acts are now practical acts, instead of doxastic acts, and we’ll assume that preferences between them are determined by their expected utility. The Practical Argument for conditionalization then goes as follows:

Suppose, for reductio, that conditionalization is false, so that for some E and A, C_E(A) ≠ C(A|E). Assume that our agent can perform one of the following two acts, where acts are functions from worlds to the utility, in that world, of performing the act:

$𝒜(w)=\{\begin{array}{l}1-C_E(A)\text{ if }w\in A\hfill \\ -C_E(A)\text{ if }w\notin A\hfill \end{array}$

and

$𝒪(w)=0\text{ for all }w.$

We can think of $\mathcal{A}$ as accepting a $1 bet on A for the price of C_E(A), and of 𝒪 as declining to bet.

Since $C_E(A)\ne C(A\mid E)$, it follows that either $E{V}_{C(\cdot \mid E)}𝒜>E{V}_{C(\cdot \mid E)}𝒪$ or .²⁹ Thus, by the conditional expectation lemma, it is not both the case that (a) $\langle E,𝒜\rangle \succcurlyeq \langle E,𝒪\rangle$ and (b) $\langle E,𝒪\rangle \succcurlyeq \langle E,𝒜\rangle$. However, by conditional completeness, one of (a) or (b) is true, so that by definition of strict preference (≻) it follows that either $\langle E,𝒜\rangle \succ \langle E,𝒪\rangle$ or $\langle E,𝒪\rangle \succ \langle E,𝒜\rangle$.

Now applying epistemic admissibility, it follows that the agent must either perform $\mathcal{A}$ or 𝒪 after learning that E. But $\mathcal{A}$ is a fair bet from the point of view of C_E (i.e. $\mathcal{A}$ and 𝒪 have the same expected utility for the agent after learning that E)³⁰ so that the agent is permitted to perform either. Thus, our assumption must be wrong: it cannot be the case that for some $E,A,C_E(A)\ne C(A\mid E)$. conditionalization must be true.

Two remarks on this argument: First, just like the New Accuracy Argument, it is not restricted to experiments with transparent evidence. Second, note that by applying epistemic admissibility, we implicitly assumed that the agent has exactly two available acts: $\mathcal{A}$ and 𝒪. How does this justify conditionalization in a situation where those acts aren’t available, or where others are? Here we can take a page from the DDBA, which is meant to show that one should always conditionalize on one’s evidence, not just when a clever bookie is in the vicinity and the only available options are to accept their bet, or not. Proponents of the DDBA, such as David Lewis, argue that the fact that the agent would accept a dutch book if they faced that choice means that they have “contradictory opinions about the expected value of the very same transaction” (Lewis, 1999, p. 405), which is a kind of irrationality, not in the agent’s actions, but in their preferences. The same can be said about this argument: the fact that the agent is indifferent between 𝒪 and $\mathcal{A}$, even though before learning they strictly preferred one of $\langle E,𝒪\rangle$ and $\langle E,𝒜\rangle$ to the other, shows that they have plan incoherent preferences even though they aren’t able to perform those acts, or are able to perform others.³¹

8.3 Discussion

My two arguments can be seen, roughly, as generalizations of the standard arguments to experiments that may contain opaque evidence, though the Practical Argument is more loosely related to the DDBA. They generalize the arguments in a different way than Hild and Schoenfield do, though, by adopting a different account of admissibility. Those who, like Hild and Schoenfield, consider the admissible plans to be those with $\mathbb{L}E$ as their condition, are really answering the question: What is the optimal way to react to the fact that one has learned that E?. My arguments, on the other hand, answer a different question: What is the optimal way to react to the fact that E is true?. It should be no surprise that our answers differ accordingly: I think one ought to conditionalize on E, while they conclude that one ought to conditionalize on $\mathbb{L}E$.

This doesn’t, I think, reflect well on the arguments for a-e conditionalization. Arguably, we should want our update rule to help explicate the idea that one should believe what one’s evidence supports. If so, what should matter is the evidential proposition itself (E), not the fact that it is one’s evidence ($\mathbb{L}E$). That is because, intuitively, whether E supports p depends on the logical or inductive relationship between E and p, not on the logical or inductive relationship between $\mathbb{L}E$ and p. For example, It is raining doesn’t intuitively support I have evidence about the weather to any high degree, given normal background evidence, because there is no logical or strong inductive connection between the fact about the weather and the fact about my mind. That is the case even though My evidence says that it is raining entails the claim that I have evidence about the weather.³²

As for the differences between my arguments, each has its own advantage. The Practical Argument, I believe, has an important advantage over the New Accuracy Argument. The idea that we should think of the rationality of epistemic principles as determined by their conduciveness to accurate belief is highly controversial.³³ The Practical Argument allows us to sidestep this controversy, since the only assumption it makes about rational credences (apart from them being probabilities) is that they are connected to preferences about acts and plans via expected value calculations. This makes the Practical Argument interesting independently of the issue of externalism. On the other hand, if one thinks that facts about epistemic rationality are explanatorily prior to facts about practical rationality, the New Accuracy Argument seems better poised to explain, rather than just establish, the rationality of conditionalizing.

8.4 Comparison to Another Solution

Dmitri Gallow (2021) suggests a different way of reconciling the Accuracy Argument with externalism.³⁴ He gives an accuracy-based argument for an update rule which is consistent with externalism, but differs from both conditionalization and a-e conditionalization.³⁵ His key idea is that one can evaluate plans not by the expected accuracy of correctly following them, as I have done, following most of the literature, but rather by the expected accuracy of adopting the plan, where the latter takes into account the possibility that one will not follow the plan correctly.³⁶ He shows that if expected accuracy is calculated in this way, his update rule maximizes expected accuracy.

While our update rules differ, this doesn’t necessarily mean that we disagree across the board. Instead, they are different kinds of rules: Gallow’s rule concerns a less idealized standard of rationality, which takes possible fallibility into account, while my rule is about ideal rationality, which is only sensitive to the agent’s lack of information, and not to the possibility that they are cognitively limited.³⁷ We do disagree about the ideal case, however. As Gallow acknowledges, his rule collapses into a-e conditionalization for ideal agents who know that they will correctly follow their plan.³⁸ For Gallow, then, such agents can never be uncertain of their evidence, even when it is opaque as in Here’s a Hand. Thus, I reject Gallow’s argument for the same reason that I reject Hild’s and Schoenfield’s arguments: in cases of opaque evidence the agent has not learnt the condition of their update plan and so is not required to implement it. My view thus has an advantage as far as the externalist is concerned. For me one can be rationally uncertain of one’s evidence for the same reason one can be rationally uncertain about anything else: one’s evidence may not settle the matter. For Gallow this is not enough for uncertainty about evidence to be rational. One must also be uncertain about one’s capacity to implement plans.

8.5 Is Conditionalization Still a Coherence Norm?

I end by considering a more general worry about the relationship between externalism and Bayesianism.³⁹ Standard Bayesian arguments such as accuracy or dutch book arguments are often thought to show that an agent who doesn’t conform to the standard Bayesian norms is incoherent in that they are doing something that’s suboptimal from their own perspective, for example, by accepting a Dutch Book, or by having beliefs that are accuracy-dominated. But if one can have opaque evidence, conditionalizing can’t always be a matter of doing what’s best from one’s perspective, since in the Bad Case, for example, one doesn’t know whether it is best to conditionalize on EXP or EXP ∧ HAND.

In reply, an externalist will insist on the distinction between what’s best from one’s perspective and what one can know (or be certain) is best from one’s perspective. My arguments do show that a non-conditionalizer is incoherent in that they are doing something that’s bad by their own lights, even in cases with opaque evidence. In Here’s a Hand, if your plan preferences are rationally formed, you will prefer the plan to conditionalize on EXP to all other plans for EXP, so that by failing to conditionalize on EXP in the Bad Case you are plan incoherent — you fail to implement the plan that’s best by your own lights. The fact that your evidence is opaque only means that you don’t know exactly what your perspective is, since your perspective is partly constituted by your evidence, so that you aren’t certain of what is best by your lights.

One may also worry that this leaves the agent without guidance in such cases. However, precisely for this reason, externalists typically deny that rational norms must always give us guidance, at least in the strong sense that one’s evidence must always warrant certainty about what they require.⁴⁰ Some externalists go so far as to deny that there are any norms that can always provide guidance in this sense (Williamson, 2000, ch. 4). Indeed, a similar worry arguably arises for other Bayesian arguments even without the possibility of opaque evidence, as long as one can be rationally uncertain of other factors that make up one’s perspective, such as one’s credences or values. For example, the Accuracy Argument for Probabilism (Joyce, 1998) shows that every non-probabilistic credence function is accuracy-dominated, so that for any probabilistically incoherent agent there is always a credence function that is guaranteed to be more accurate than their credences. But a non-probabilistic agent who doesn’t know what their credences are can fail to know that there is a more accurate credence function, or which function that is.