1. Introduction
Our topic concerns two puzzles involving desire reports. They can be illustrated by considering the following case:
Coins: Three fair coins will be flipped, and Bill’s reckless brother has bet the family fortune on the outcome. If the first coin lands heads, and the second or third coin lands tails, the entire fortune will be lost. If all three coins land heads, the fortune will be doubled. If the first coin lands tails, nothing happens, i.e., nothing is lost (or gained).
(1) is easily heard as true in this scenario:
(1) Bill wants all three coins to land heads.
After all, if all three coins land heads, Bill knows that the fortune will be doubled, and he would certainly like that. But by the same token, (2) is also easily heard as true:
(2) Bill wants the first coin to land tails.
After all, if the first coin lands heads, Bill knows there’s a good chance that the fortune will be lost, and he certainly would not like that.
However, (1) and (2) cannot be felicitously conjoined (as indicated by the ‘#’ preceding the example):
(3) # Bill wants all three coins to land heads, and he wants the first coin to land tails.
(3) sounds incoherent. But this is surprising: if both (1) and (2) are true, then why can’t they be put together, as in (3)? Let us call this the three heads and tails puzzle, or the 3H-T puzzle.
The second puzzle begins with the observation that (4) is unacceptable in context:
(4) # Bill wants the first coin to land heads.
A natural response to (4) would be: “but if the first coin lands heads, Bill knows that the fortune will likely be lost, and he definitely wouldn’t like that”. However, the negation of (4) cannot be felicitously conjoined with (1):
(5) # Bill wants all three coins to land heads, but he doesn’t want the first coin to land heads.
(5) sounds incoherent. But this is unexpected: if (1) is true and (4) is false, why isn’t the conjunction of the former along with the negation of the latter acceptable? Let us call this the three heads and not-first-heads puzzle, or the 3H- puzzle.1
In this paper, we try to solve both the 3H-T puzzle and the 3H- puzzle by developing a novel semantics for desire reports. This account is built around three ideas. First, we propose that desire ascriptions are evaluated relative to a contextually supplied set of propositions, or alternatives. ’s preference ordering over these alternatives determines the semantic value of desire reports.2 On our entry, there are no sets of alternatives relative to which the conjunctions (3) and (5) are true, which explains their unacceptability.
Second, we propose that desire reports carry a requirement to the effect that the prejacent of the ascription must be suitably related to the background set of alternatives. That is, we propose a representation condition on the prejacent. As we show, this constraint explains why the natural set of alternatives relative to which (1) is evaluated is one where the report comes out true.
Finally, we propose a dominance condition concerning the subject’s ranking of the alternatives. If there is some top-ranked -entailing alternative by ’s lights, then must prefer every -entailing alternative to every -entailing alternative, i.e., the -entailing alternatives must dominate the -entailing alternatives. As we show, this explains why (4) is unacceptable. Overall, we argue that our theory provides us with an elegant resolution of our puzzles, and yields a promising approach to desire.
The paper is structured as follows. In §2, we show that existing theories of desire ascriptions fail to provide solutions to our puzzles. Then, in §3, we develop our theory in several stages. Finally, §4 concludes by discussing the relationship between desire verbs and deontic modals.
2. Existing Accounts
In this section, we consider how some existing approaches to desire fare with respect to our puzzles. To this end, we consider two influential accounts: the monotonic analysis of von Fintel (1999) (§2.1) and the decision-theoretic semantics of Levinson (2003) (§2.2). We argue that although these accounts can explain some aspects of our puzzles, neither provides us with satisfying solutions to them.3
2.1 Von Fintel’s (1999) Account
In a tradition that begins with Hintikka (1962), many attitude verbs are given a quantificational semantics involving a lexically-determined accessibility relation. For instance, relative to a world w, ‘believe’ denotes a relation that holds between an agent S and a proposition p just in case every world compatible with S’s beliefs in w is one in which p is true, i.e., every world in ’s belief set, denoted Dox, is a p-world. Von Fintel treats ‘want’ similarly, i.e., as a function such that ‘Bill wants Ann to leave’ is true at world w just in case every world that conforms to what Bill desires in w—every world in Bill’s desire set in w—is one where Ann leaves.
Von Fintel puts constraints on which worlds can appear in a subject’s desire set. He assumes that a subject’s desires generate a preference ordering over possible worlds: for any subject S: iff is more desirable to than in . is a strict partial order. The idea is that the subject’s desire set is constrained by their beliefs: the subject’s desire set is comprised of all and only their top-ranked belief worlds, as ordered by .4
Specification of Desire Set
For any subject S and world w: S’s desire set Bul
Von Fintel’s account can be expressed as follows:5
Von Fintel’s semantics for want
wants is true in iff Bul
Now, let us consider our puzzles from §1. The 3H-T puzzle concerned the fact that both (1) and (2) are acceptable in the Coins scenario, but (3) is not:
Bill wants all three coins to land heads.
Bill wants the first coin to land tails.
# Bill wants all three coins to land heads, and he wants the first coin to land tails.
The acceptability of both (1) and (2) poses an immediate problem for this account. All three coins land heads and The first coin lands tails are incompatible propositions. So, if every world in Bill’s desire set is one where all three coins land heads, it’s not the case that every world in Bill’s desire set is one where the first coin lands tails. Similarly, if every world in Bill’s desire set is one where the first coin lands tails, it’s not the case that every world in Bill’s desire set is one where all three coins land heads. It follows that (1) and (2) can’t be true together, so at least one of these reports is predicted to be false and thus infelicitous.
One possible response here is to maintain that (1) and (2) are evaluated relative to different preference orderings over worlds. The idea is that the ordering on which (1) comes out true ranks highly those worlds in which all three coins land heads. By contrast, the ordering on which (2) comes out true ranks highly those worlds in which the first coin lands tails. Moreover, it could be maintained that this ordering is determined by context, which would explain why (3) is unacceptable: given a fixed context, there is no single ordering relative to which the conjunction comes out true.6
It should be noted that the appeal to shifting orderings has precedent in the literature on desire reports. It is plausible that virtually all theorists need to make use of something like this mechanism in order to explain so-called “conflicting desires” (Crnič, 2011, 170–172). For instance, suppose that all my friends are at a party, and that I’d like to see them. But suppose also that I’m eager to stay home and finish working on a paper. If someone asks me ‘Would you like to go to the party?’, I can felicitously respond by saying ‘I do and I don’t’. It seems difficult to make sense of my response without availing oneself of some sort of preference shift: my positive reply is warranted relative to a preference ordering that takes seeing my friends into account, while my negative reply is warranted relative to a preference ordering that takes finishing my paper into account. Evidence that my replies are accessing different sorts of preferences comes from the fact that I can preface each with phrases such as ‘in one way’, ‘part of me’, and ‘in some sense’:
| (6) |
|
Although the mechanism of preference shift might be needed to handle conflicting desires, we don’t think that it provides a compelling response to the 3H-T puzzle. Our central concern is straightforward: it just doesn’t seem plausible that Bill has two different sorts of preferences in the Coins scenario—all he cares about is losing and gaining money. That is, there is only one thing he values here, not two. This makes the Coins scenario disanalogous to the party example above. Indeed, notice that one cannot felicitously preface (1) and (2) with ‘in one way’ or ‘part of Bill’:
| (7) |
|
This is surprising if the acceptability of (1) and (2) is to be explained by variation in Bill’s preference ordering. To be clear, the account that we develop in §3 also appeals to a context shift in order to solve the 3H-T puzzle. So, we are not against this general feature of the variable-preference response. Importantly, however, on our proposal what shifts is not the subject’s preferences, but rather the objects that are being ordered.
We also want to register a broader concern with any response to the 3H-T puzzle that has (2) coming out true on von Fintel’s semantics. On this account, desire reports are closed under logical consequence, i.e., they are upward monotonic:
-
Monotonicity If then
Thus, in any context where (2) is predicted to be true, (8) is predicted to be true as well:
(8) # Bill wants the first coin to land tails, so he wants a result other than three heads.
But it is difficult to hear this sentence as anything but unacceptable.7 Similarly, the ordering on which (2) comes out true ranks highly those worlds in which the first coin lands tails. So given a natural semantics for preference claims, in such contexts we would expect (9) to also be true:
(9) # Bill prefers the first coin landing tails to all three coins landing heads.
However, we find it very hard to hear this sentence as good.
As for the 3H- puzzle, it involves the fact that although (4) is unacceptable, the negation of this sentence cannot be felicitously conjoined with (1) (‘Bill wants all three coins to land heads’):
(4) # Bill wants the first coin to land heads.
(5) # Bill wants all three coins to land heads, but he doesn’t want the first coin to land heads.
Given Monotonicity, von Fintel has a straightforward explanation for why (5) is bad: it can never be true. But it is less obvious how the account can explain why (4) is unacceptable. Let us suppose that the 3H-T puzzle has been resolved, so that there are contexts where (1) comes out true. Then, given Monotonicity, there should be contexts where (4) is true as well. Why, then, does the report sound bad? One idea is that (4) is infelicitous because it generates a false implicature: since (4) is less informative than (1), an utterance of the former suggests that the latter is false. The model here could be the scalar implicature triggered by ‘some’: an utterance of ‘Ben drank some of the whiskey’ suggests that the logically stronger ‘Ben drank all of the whiskey’ is false. Thus, in contexts where ‘Ben drank all of the whiskey’ is plausibly true, an utterance of ‘Ben drank some of the whiskey’ will be infelicitous, but nevertheless true.
However, it is characteristic of these sorts of pragmatic effects that they disappear in certain environments. For instance, the implicature is canceled in (10a) and (10b):
| (10) |
|
By contrast, to our ears both (11a) and (11b) sound unacceptable:
| (11) |
|
This suggests to us that the infelicity of (4) is not due to a false implicature. Of course, we do not take this to be a decisive argument against an implicature-based analysis. But we do think that there are significant challenges to developing a successful response in this vein.
Before moving on to consider Levinson’s semantics, it is worth pausing to contrast our puzzles with a different problem that has been raised for von Fintel’s account. Several authors have observed that the (a)-examples below do not seem to imply the (b)-examples (Stalnaker, 1984; Heim, 1992):
| (12) |
|
| (13) |
|
These patterns seem to present a straightforward challenge for Monotonicity-validating views. Since I die peacefully entails I die, such views appear to predict that, e.g. (12a) should entail (12b). However, most existing accounts—whether Monotonicity-validating or not—maintain that wants can be true only if neither believes nor (Heim, 1992). That is, needs to be diverse with respect to the subject’s beliefs. The (b)-examples above plausibly contravene this diversity condition: we all know that we will die one day, and presumably Bill believes that a murder was committed. Thus, if existing accounts are correct, these failures of entailment don’t necessarily speak against Monotonicity-validating views.8
We aren’t moved by a belief constraint on desire reports. It has been recognized for some time (though it is often ignored) that subjects can want things they are certain won’t obtain, as well as things they are certain do/will obtain:
| (14) |
|
| (15) |
|
These examples are perfectly felicitous, but they are difficult to account for given standard belief constraints on want ascriptions.9 That said, we still don’t think that the examples in (12) and (13) pose a significant challenge for von Fintel’s account. For instance, one could maintain that the subject’s desire set is a subset of a background modal base, which needn’t be identical with their belief set (Rubinstein, 2012). Furthermore, one could say that when, e.g., (12b) is evaluated, the background modal base shifts so that worlds where I live forever become relevant. Relative to this expanded modal base, von Fintel’s account predicts that the conjunction should be false (Grano and Phillips-Brown, 2022). We think that proponents of von Fintel’s semantics would do well to appeal to a modal base shift in order to handle these examples, but we’ll leave them to develop this response further. Our central point is that there are significant differences between our puzzles and the examples in (12) and (13). In the first place, all of the relevant prejacents in our puzzles are diverse with respect to the subject’s beliefs. But even if one isn’t inclined to endorse belief constraints on desire reports, we think that however one spells out the dynamics of modal base shift, our puzzles won’t be resolved by appealing to such shifts.
2.2 Levinson’s (2003) Account
Now let us consider Levinson’s decision-theoretic account of desire reports. On this proposal, the desirability of a proposition for a subject is tied to the expected value of this proposition for . The expected value of for is the utility of for weighted by ’s subjective probabilities (Jeffrey, 1965). More precisely, wants is true just in case the expected value of , for , outweighs the expected value of :10
Levinson’s semantics for want
wants is true in iff
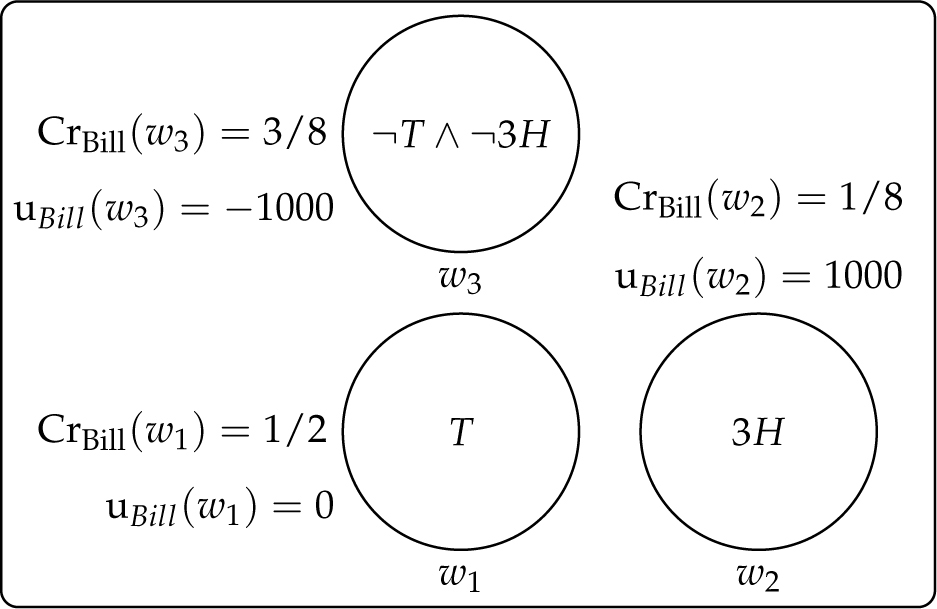
Since we think that this account has few plausible responses available to our puzzles, we will be relatively brief here. First, let us suppose that Bill’s credences/utilities in the Coins scenario are as follows ( denotes the proposition that all three coins land heads, and denotes the proposition that the first coin lands tails):
To repeat, the 3H-T puzzle concerns the fact that both (1) and (2) are acceptable in the Coins scenario, but (3) is not:
(1) Bill wants all three coins to land heads.
(2) Bill wants the first coin to land tails.
(3) # Bill wants all three coins to land heads, and he wants the first coin to land tails.
A routine calculation confirms that , and that . Thus, this semantics predicts that both (1) and (2) should be true. So given a standard meaning for natural language conjunction, the account predicts that (3) should be true as well. But then it is unclear why this sentence should be unacceptable.
As for the 3H- puzzle, it involves the fact that both (4) and (5) are infelicitous:
(4) # Bill wants the first coin to land heads.
(5) # Bill wants all three coins to land heads, but he doesn’t want the first coin to land heads.
It is easy to show that . So Levinson’s account predicts that (4) should be false. Since (1) is predicted to be true, (5) is then predicted to be true as well. So we would expect this conjunction to be acceptable, contrary to observation.11,12
It is worth noting that conjunctions that have the form of (5) have been used by proponents of von Fintel’s semantics to argue against accounts that invalidate Monotonicity, e.g., Levinson’s theory.13 The idea is that if p entails q, then conjunctions of the form wants p, but S doesn’t want are always unacceptable. However, such conjunctions can be true on views that reject Monotonicity. So, if Monotonicity-rejecting views are correct, it is unclear why these sentences should be infelicitous. By contrast, accounts that validate Monotonicity can offer a straightforward explanation: such conjunctions are simply false (von Fintel 1999; Crnič 2011). As should be clear, we think the picture is more complicated than this argument suggests. The real challenge from conjunctions of the form wants p, but S doesn’t want (where entails ) arises from the 3H- puzzle: it involves cases where both wants and wants p, but S doesn’t want are unacceptable. As we’ve shown, this puzzle poses a problem for Monotonicity-accepters and Monotonicity-deniers alike.
In this section, we considered how existing accounts fare with respect to our puzzles. Although our survey hasn’t been exhaustive, we hope to have provided at least some motivation for thinking that these puzzles are genuine, and are not easily solved by existing theories. In the next section, we will try to explain these phenomena by developing a novel approach to desire reports.
3. The Meaning of want
In this section, we present our positive proposal in several stages. First, we provide a basic entry that captures some of the central features of our account (§3.1). Then we propose a constraint that governs the relationship between the prejacent of want reports and the set of possibilities relevant for the evaluation of these reports (§3.2). Finally, we posit a dominance condition on desire ascriptions (§3.3).
3.1 The Basic Proposal
Like von Fintel’s account considered in §2.1, we also propose that desire reports are evaluated relative to a subjective preference ordering over a domain of objects. However, one of the key features of our account is that we take this preference ordering to range over propositions rather than worlds. There are several ways of developing this idea, but we will implement it in a fairly simple way so as not to distract from our central arguments.
We will say that is a set of alternatives if it is a set of pairwise incompatible propositions. So, if , then . To illustrate, let ANN, MARY, PETE, and SUE represent the propositions that Ann wins the race, Mary wins the race, Pete wins the race, and Sue wins the race, respectively. Then is a set of alternatives.
We propose that the set of objects that is relevant for the evaluation of a desire ascription wants is a set of contextually supplied alternatives.14
Given a set of alternatives and a world , is an ordering function from individuals to orderings over . It is assumed that is a strict partial order. Intuitively, represents ’s preference ordering over in , denoted .15 For instance, Bill’s preferences over are represented below:
We propose that desire reports are evaluated relative to a contextually determined ordering function. Given an ordering , the function BEST() returns the maximal elements in the ordering.16 For instance,best.17
Our first-run account can be expressed as follows:
Account 1
S wants p is true relative to iff for every :
In short, S wants p is true just in case all of the top-ranked alternatives in S’s preference ordering entail .
To get a feel for how this account works, consider the following example adapted from Levinson (2003):
Insurance: Sue is deciding whether to take out house insurance. She estimates that the chances of her house burning down are . But the results would be calamitous: she’d lose her home which is valued at . Comprehensive home insurance would cost her . Sue has a meeting with her insurance broker this afternoon, so she needs to decide what she wants to do.
(16) Sue wants to buy insurance.
If Sue is like most of us, (16) is true: even though she thinks it’s likely that her house won’t burn down, there is a small possibility that it does, and the badness of this possibility outweighs the cost of buying insurance.
Examples such as (16) are often taken to pose a problem for accounts that ground the semantic value of desire reports in preference orderings over worlds, e.g., von Fintel’s account. Given such an ordering over worlds, the problem is that in order to make (16) come out true, it must be claimed that Sue’s most preferred worlds are ones where she buys insurance. But intuitively this isn’t the case; it’s quite clear that Sue most prefers worlds where she spends no money on insurance (and there’s no fire).18 However, alternatives are relatively coarse-grained entities. So, even if there are some worlds in an alternative that are bad by ’s lights, can still rank higher than the other alternatives. For instance, let us suppose that the relevant set of alternatives in the Insurance scenario is , where INSURANCE and are the propositions that Sue buys insurance, and that she doesn’t buy insurance, respectively. Moreover, let us suppose that Sue’s preferences over these alternatives look as follows:
In this case, Account 1 predicts that (16) should be true.
At this point, two natural meta-semantic questions arise for Account 1: (i) how exactly the set of alternatives gets determined in context, and (ii) how the subject’s ordering over alternatives is structured. We won’t be able to provide a complete answer to the first question here. This is obviously an important matter, but it must be left for future work. That said, we will try to show that moving from orderings over worlds to orderings over propositions yields several explanatory benefits. Indeed, such benefits were already displayed by the ease with which Account 1 can handle “insurance cases” such as (16). So, even though we will leave some meta-semantic details to be filled in, we hope to make it plausible that alternative-sensitivity can do important work in capturing the patterns exhibited by desire reports.19
As for the second issue concerning how the subject’s preference ordering is structured, a useful model treats this ranking as determined by expected value.20 That is, for alternatives : when . This would explain why, for example, Sue ranks INSURANCE above in the Insurance example. If something like this is correct, then it has interesting consequences for the nature of desire. Theories that analyze desire in terms of subjective preference orderings, and decision-theoretic analyses that tie the desirability of a proposition to its expected value, are often taken to be in competition with each other (Lassiter 2011; von Fintel 2012). However, if we opt for a framework in which the ranking over alternatives is determined by decision-theoretic considerations, then this isn’t the case. The central elements of both accounts would be needed.
Now let us see how Account 1 does with our puzzles. To repeat, the 3H-T puzzle concerns the fact that both (1) and (2) are acceptable in the Coins scenario, but (3) is not:
(1) Bill wants all three coins to land heads.
(2) Bill wants the first coin to land tails.
(3) # Bill wants all three coins to land heads, and he wants the first coin to land tails.
We propose that the key to understanding what is going on here is that (1) and (2) are being evaluated relative to different sets of alternatives. More specifically, (1) is evaluated relative to a relatively fine-grained set of alternatives. For instance, one possibility is that this set is , where 3H is the proposition that all three coins land heads, T is the proposition that the first coin lands tails, and OTHER is the proposition that the coins land in any of the remaining configurations. Bill’s preferences over are as follows:
Relative to , (1) will be true, since 3H is preferred to any of the other alternatives.
By contrast, (2) is evaluated relative to a relatively coarse-grained set of alternatives, e.g., , where H is the proposition that the first coin lands heads. Bill’s preferences over are as follows:
Relative to , (2) will be true, since T is preferred to H.
However, observe that there is no set of alternatives relative to which both (1) and (2) are true. Relative to , (2) is false, since 3H doesn’t entail T. And relative to , (1) is false, since T doesn’t entail 3H. So, assuming that both conjuncts in (3) are evaluated relative to the same set of alternatives, Account 1 predicts that this conjunction cannot be true.21
As for the 3H- puzzle, recall that this involves the fact that both and (5) are infelicitous:
(4) # Bill wants the first coin to land heads.
(5) # Bill wants all three coins to land heads, but he doesn’t want the first coin to land heads.
Just as for (2), we suggest that (4) is evaluated relative to . In that case, the report is predicted to be false. And observe that there is no set of alternatives relative to which both conjuncts of (5) are true. Relative to , (4) is true, since 3h entails h. And relative to , (1) is false, since t doesn’t entail 3h. So, assuming that both conjuncts in (5) are evaluated relative to the same set of alternatives, the conjunction is predicted to be false.
Account 1 goes a fair way to resolving our puzzles: it predicts that neither (3) nor (5) can be true, which accounts for their unacceptability. But it still leaves some questions unanswered. These are: (a) why should (1) be evaluated relative to , and (b) why should (2) and (4) be evaluated relative to ? We will resolve these issues over the next two subsections.
3.2 Representation
In §2.1, we saw that even if von Fintel’s account could somehow allow (2) (‘Bill wants the first coin to land tails’) to be true, it would then predict that the clearly unacceptable (8) should be true:
(8) # Bill wants the first coin to land tails, so he wants a result other than three heads.
Unfortunately, the same problem arises for Account 1. (2) is true relative to , so ‘Bill wants a result other than three heads’ should also be true relative to , since t entails that the coins land in a pattern other than three heads.
Intuitively, what goes wrong with (8) is that the proposition the result is other than three heads makes salient certain distinctions that are not in play when we are evaluating the first conjunct, i.e., (2). Put another way, when we hear (2) as true, we are “backgrounding” the outcome where all the coins land heads. We can make this more precise through the following definition. Given a set of alternatives and proposition , let us say that is represented by just in case every alternative in either entails or entails .22 For instance, the proposition that the first coin lands tails is represented by , but the proposition that the outcome is other than three heads is not, since h neither entails this proposition nor its negation.
We propose adding a representation requirement to the semantics of desire reports. More precisely, we will include this as a definedness condition on desire ascriptions.23 The account then looks as follows:
Account 2
wants is defined relative to only if is represented by If defined, wants is true relative to iff for every :
Account 2 explains why (1) is evaluated relative to so long as we take on board the following widely accepted principle: hearers tend to interpret sentences so as to avoid presupposition failure. That is, within reasonable limits, hearers will make the assumptions necessary to avoid undefinedness.24 For instance, even if I suspect that you have no siblings, I will come to assume that you have a sister once I’ve heard you utter (17):
(17) I have to fetch my sister from the airport tomorrow.
That is, the presupposition triggered by the possessive ‘my sister’, namely that I have a sister, is taken to hold when evaluating (17).
To repeat, we are supposing that there are two relevant sets of alternatives in the Coins scenario, namely and . (1) fails to be defined relative to , since the proposition All three coins land heads isn’t represented by this set of alternatives. But (1) is defined relative to . Assuming that hearers will try to avoid interpretations that result in presupposition failure, they will then be moved to evaluate (1) relative to rather than . This is exactly the result that we wanted.
We can also explain why (2) should sound true. Even though the proposition The first coin lands tails is represented by both and , there is an important difference between these two sets of alternatives. (2) is true relative to , but false relative to . So, assuming that hearers generally tend to interpret speakers in a way that makes their utterances come out true—the so-called “principle of charity”—we would expect there to be a tendency to evaluate context-sensitive expressions relative to parameters which make the speaker’s assertions true.25 In particular, then, by default we should expect (2) to be evaluated relative to rather than .
However, the representation requirement and the principle of charity still don’t explain why (4) should be evaluated relative to rather than . After all, The first coin lands heads is represented by . Moreover, (4) actually comes out true relative to this set of alternatives. So, a different sort of explanation is needed to explain why the report sounds bad. We turn to this next.
3.3 Dominance
What is crucial to providing a complete solution to our puzzles, we suggest, is recognizing that desire reports carry a dominance requirement. We introduce this idea in two stages. We begin by discussing a fairly simple condition but raise some problems for it. Then we present a more sophisticated notion of dominance.
On the semantics from §3.2, if wants is defined, then all that matters for its semantic value is whether or not all of the top-ranked alternatives entail . But we could require something stronger. We could require not just that every top-ranked alternative entails , but that every p-entailing alternative outranks every -entailing alternative. When this happens, let us say that dominates (with respect to the background parameters):
Dominance
Given a set of alternatives , ordering over , and proposition , dominates iff for every such that ⊆ , and every such that : .
One could add a dominance requirement to our semantics from §3.2. More specifically, it could be imposed as an additional presupposition or definedness condition triggered by desire reports. This yields the following entry:
Account 3
wants is defined relative to only if
is represented by ; and
dominates
If defined, wants is true relative to iff for every :
This semantics explains why (4) should be unacceptable. Recall that Bill’s preference ordering over looks as follows:
While Bill’s preferences over are:
It is easy to see that the proposition The first coin lands heads dominates on neither nor .26 In particular, other entails that the first coin lands heads, but this alternative is ranked below t in . Thus, Account 3 predicts that (4) should suffer from presupposition failure when evaluated relative to either or .
Although Account 3 captures the infelicity of (4), this entry isn’t quite right. One problem is that it generates problematic truth-conditions for negated desire reports. To bring this out, consider the following scenario:
Dinner: I’m meeting my friend for dinner. There are three items on the menu: spaghetti bolognese, lasagna, and chicken. I’m going to be late, so my friend—who has no idea about my preferences—is going to order for me. Given my past experience, I like the spaghetti most, I find the chicken to be average, and I hate the lasagna.
(18) I don’t want my friend to order chicken for me.
18 is perfectly acceptable. However, Account 3 predicts that the report should suffer from presupposition failure on the most natural set of alternatives. The relevant set of alternatives is , where SPAGHETTI is the proposition that my friend orders spaghetti for me, LASAGNA is the proposition that my friend orders lasagna for me, etc. My preferences look as follows:
Note that CHICKEN fails to dominate on this set of alternatives. Now, one feature of presuppositions is that they project from certain embedded environments, namely negation.27 Thus, on Account 3 the negated report (18) also presupposes that CHICKEN dominates. So, given that this presupposition is not satisfied, and cannot be accommodated, (18) is predicted to be unacceptable.28
Some might be tempted to respond by making the dominance condition a regular entailment of desire reports rather than a presupposition. But this would make it too easy for these ascriptions to be false. For instance, consider (19) in the Dinner scenario:
(19) I don’t want my friend to order pasta for me.
The account we are considering predicts that regardless of the relative expected value of pasta and chicken, (19) should have a true reading. In particular, it incorrectly predicts that (19) should have a true reading in contexts where the expected value of pasta is greater than the expected value of chicken.29 For if the dominance requirement was a regular entailment, then ‘I want my friend to order pasta for me’ would simply be false on the natural set of alternatives, since both SPAGHETTI and LASAGNA entail that my friend orders pasta for me, and CHICKEN entails that my friend does not order pasta for me. But then would be true on the natural set of alternatives.
Instead, we suggest responding by weakening the dominance condition. Intuitively, we want dominance to take effect in a report such as (4), but not in a report such as (18). One way of achieving this is by appealing to a conditional version of dominance which only requires that dominates if there is some top-ranked -entailing alternative. More precisely ( denotes the material conditional):
Conditional dominance
Given a set of alternatives , ordering ≻ over , and proposition , conditionally dominates iff there is some ∈ BEST(≻) such that dominates.
Our final entry is the following:30
Meaning of want⌜S wants p⌝ is defined relative to only if
p is represented by ; and
p conditionally dominates
If defined, ⌜S wants p⌝ is true relative to iff for every : q ⊆ p
This semantics also explains why (4) (‘Bill wants the first coin to land heads’) is unacceptable in the Coins scenario. The proposition The first coin lands heads (trivially) conditionally dominates on , since is top-ranked. But this means that the report is straightforwardly false on this set of alternatives. By contrast, the proposition The first coin lands heads does not conditionally dominate on , since is top-ranked and entails that the first coin lands heads. Thus, (4) is predicted to be infelicitous on either set of alternatives. Overall, this entry explains all of the key data points undergirding our central puzzles. Moreover, it correctly predicts that (18) should be true in the Dinner scenario, on the natural set of alternatives. For the proposition My friend orders chicken for me (trivially) conditionally dominates given that is top-ranked.
Some might worry that imposing a conditional dominance constraint still yields a semantics that is too strict. For instance, consider (20) in the Dinner scenario:
(20) I want my friend to order a pasta dish for me.
(20) sounds true, but our view seems to predict that it should be unacceptable. The worry is that the proposition My friend orders a pasta dish for me doesn’t conditionally dominate on . Moreover, maintaining that the report is evaluated relative to the coarse-grained set of alternatives doesn’t help. For we can suppose that the expected value of PASTA is less than or equal to the expected value of . In this case, we would predict that (20) should be false on .
In response, we maintain that the felicity of (20) can be traced to an ambiguity in the interpretation of indefinite descriptions. Sometimes these expressions can be read “specifically”, and concern particular objects or individuals.31 We think that this is exactly what’s happening with ‘a pasta dish’ in (20). One simple way to capture this is to assume that the indefinite in (20) takes wide-scope at the level of logical form:
(21) There is a particular pasta dish such that I want my friend to order for me.
Assuming that the particular dish here is spaghetti, the prejacent is verified by the proposition My friend orders spaghetti for me. And this proposition does conditionally dominate on . So in this case (20) is predicted to be true. That this account of (20) is on the right track is suggested by the fact that minimal variants which do not feature indefinites are easily heard as unacceptable:32
(22) I want my friend to order pasta for me.
A natural response to (22) would be ‘But what if your friend orders lasagna for you, which you hate?!’. This contrast is quite striking, and further confirms the general shape of our account.33
It is worth drawing out several further features of our entry. First, our semantics makes some interesting predictions in cases where two or more alternatives are tied best. For example, suppose that Paris and Rome are your two favorite holiday destinations. You’d be thrilled to go to either, but don’t prefer one over the other. In this context, both (23a) and (23b) are unacceptable:
| (23) |
|
Let us suppose that the relevant set of alternatives is , where is the proposition that I holiday in Paris, and is the proposition that I holiday in Rome. Then neither alternative conditionally dominates on , and we predict that both reports will be undefined.34
Second, our account goes some way to explaining an observation by Crnič (2011, 166) to the effect that disjunctions in the scope of desire reports give rise to an “acceptability inference” regarding both disjuncts. For instance, neither (24a) nor (24b) are felicitous:
| (24) |
|
We can explain this so long as we assume that these reports are being evaluated relative to something like , where is the proposition that Ann wins, is the proposition that Mary wins, etc.35 Then, if the first conjunct in (24a) is true, the conditional dominance condition will require (i) that both and are the best alternatives, or (ii) that the relative ranking of the alternatives is ≻ ≻ , or (iii) that the relative ranking of the alternatives is . If (i) or (ii) hold, then the second conjunct in (24a) will be undefined, since the proposition Ann loses will fail to conditionally dominate. And if (iii) holds, then the second conjunct in (24a) will be false. A similar explanation can be given of the unacceptability of (24b).
Finally, it is helpful to compare our conditional dominance condition with a feature proposed by Gajewski (2007) and Križ (2015). These authors aim to explain why ‘want’ is a so-called “neg-raiser”. This is the phenomenon whereby negated want reports are interpreted with negation taking narrow scope with respect to ‘want’, i.e., (S wants p) is interpreted as wants (Collins and Postal, 2014). For instance, an utterance of (25a) is felt to be equivalent to (26b):
| (25) |
|
To explain this, Gajewski and Križ propose a definedness condition on desire reports which, in our framework, can be stated as follows:36
Gajewski and Križ’s definedness condition for S wants p
⌜S wants p⌝ is defined relative to only if (i) every top-ranked alternative in ’s preference ordering entails , or (ii) every top-ranked alternative in ’s preference ordering entails ¬.
To see how this works, suppose that (25a) is evaluated relative to , where is the proposition that Pete wins, and is the proposition that Pete loses. Then if (25a) is true, it can’t be that Bill ranks above . Moreover, given Gajewski and Križ’s condition, it can’t be that Bill is indifferent between these two outcomes, i.e., that both and are equally top-ranked. Thus, it must be that is ranked above , and so (26b) is true.
Note that Gajewski and Križ’s condition doesn’t help to resolve our puzzles. For example, it doesn’t predict that (4) (‘Bill wants the first coin to land heads’) should be evaluated relative to . On the other hand, we think that conditional dominance could provide some insight into the phenomenon of neg-raising. For one thing, our account also predicts that (25a) and (26b) should be equivalent relative to . For if (25a) is true, then the proposition Pete wins must conditionally dominate on . But this means that Bill can’t be indifferent between and LOSE. So, must be ranked above , and (26b) must be true.
But our theory also predicts that the neg-raising inference should fail to go through in certain contexts, and that in these contexts (S wants p) should be distinguishable from wants p. There is evidence that this is a good prediction:
Coins 2: Two fair coins will be flipped, and Bill’s reckless brother has made the following bet on Bill’s behalf: if both coins land heads (HH), Bill will gain ; if the first coin lands heads and the second coin lands tails (HT), Bill will lose ; and if the first coin lands tails (T), Bill will lose . In short, the payoffs are HH = , HT = −$, and T = .
(26) a. Bill doesn’t want the coins to land HT.
b. ?? Bill wants the coins to not land HT.
We detect a difference in felicity between these reports: to our ears (26b) sounds worse than (26a). The former suggests that a tails-first outcome is preferred to the HT outcome, which isn’t the case. This is what we’d expect if we assume that the relevant set of alternatives is something like . Bill’s preferences over these alternatives look as follows:
Then (26a) will be true, but (26b) will be undefined since the proposition The coins do not land HT does not conditionally dominate on . Needless to say, much more would need to be done in order to turn these remarks into a complete theory of neg-raising, but we will leave the matter there for now. Although our treatment of neg-raising seems prima facie plausible, our central concern has been to illustrate that a fairly natural dominance condition, when coupled with our alternative-sensitive semantics, allows us to explain the puzzles from §1.
To summarize, we have tried to explain our puzzles by developing a theory of desire reports on which these ascriptions are (i) alternative-sensitive, and (ii) carry representation and dominance conditions. We think that our theory provides us with an elegant account of our data, and more generally yields a promising approach to desire.37,38
4. Wants and Oughts
Several theorists have noted that ‘want’ and ‘ought’ pattern similarly (Crnič, 2011; Lassiter, 2011; Jerzak, 2019). We add that analogues of our puzzles arise with this modal. For instance, consider a famous case adapted from Jackson and Pargetter (1986, 235):
Professor Procrastinate:
Professor Procrastinate receives an invitation to review a book. The best thing that can happen is that he says yes, and then writes the review. However, were Procrastinate to say yes, he would not in fact get around to writing the review. Thus, although the best that can happen is for Procrastinate to say yes and then write, and he can do exactly this, what would in fact happen were he to say yes is that he would not write the review. Moreover, we may suppose, this latter is the worst that can happen.
| (27) |
|
| (28) |
|
These similarities make salient the following intriguing possibility: that both desire verbs and deontic modals share an underlying semantics.39 We’ll leave this as a topic for future research. But we’ll end by noting that Cariani (2013) has put forward an account of deontic ‘ought’ that is similar, in some respects, to the semantics for ‘want’ that we have developed here. For instance, on Cariani’s proposal, ought claims are evaluated relative to a set of alternatives, as well as an ordering over those alternatives.40 This could suggest a convergence to a common semantic core.41
Notes
- Note that the conjuncts in (3) and (5) do not become more acceptable when they are placed in separate sentences. For instance, ‘Bill wants all three coins to land heads. Though he wants the first coin to land tails’ is just as unacceptable. So our puzzles really involve the fact that, e.g., (1) and (2) cannot be felicitously asserted within a single discourse. But, for convenience, we will continue to focus on conjunctions such as (3) and (5). ⮭
- We let ‘S’ range over the names of agents and let ‘S’ range over the corresponding agents denoted by ‘S’. Similarly, we let ‘p’ range over the logical forms of proposition-denoting strings and let ‘p’ range over the corresponding propositions denoted by ‘p’. ⮭
- A further influential theory of desire is the comparative desirability account of Heim (1992). Although we don’t discuss Heim’s entry in the main text, it is fairly straightforward to show that her proposal explains neither of our puzzles. ⮭
- For simplicity, we assume that Bul is non-empty so long as Dox is non-empty (this essentially corresponds to the limit assumption from Lewis (1973)). ⮭
- Von Fintel’s theory is particularly influential among linguists. See, e.g., Crnič (2011); Rubinstein (2012); Pasternak (2019). ⮭
- There is independent evidence that intrasentential context shifts are often difficult to achieve, but we won’t rehearse the data supporting this claim here. See, for example, Dorr and Hawthorne (2013) for further discussion. ⮭
- Also see Blumberg (forthcoming a) for a further objection to von Fintel’s account involving upward monotonicity. ⮭
- Note that if a diversity constraint is adopted, then Monotonicity cannot be spelled out in classical terms. Instead, defenders of Monotonicity maintain that it is Stawson valid, rather than classically valid (von Fintel, 1999). ⮭
- See (Grano and Phillips-Brown, 2022) for extensive discussion of this point. However, in what follows we will be entertaining a condition on desire reports that broadly patterns with a diversity constraint, but is not spelled out in doxastic terms (see fnn.30, 35 for discussion). But we won’t be foregrounding this condition because it won’t play a central role in explaining our central puzzles. ⮭
- , where represents ’s credences over the live possibilities in , and is an evaluation function, i.e., a function from (the set of all worlds) to the real numbers. Variants of this semantics are also endorsed by Lassiter (2011); Jerzak (2019); Phillips-Brown (2021). ⮭
- It is worth observing that neither of our puzzles are resolved on more sophisticated decision-theoretic analyses, such as the account of Phillips-Brown (2021). On this proposal, the expected value of is required to be above a contextually determined threshold value. This account still predicts that, e.g., (3) will be true in any context where is above the threshold. ⮭
- Some might be tempted to respond to (5) by appealing to the so-called “neg-raising properties” of ‘want’, i.e., the phenomenon whereby negated want reports are interpreted with negation taking narrow scope with respect to ‘want’ (Collins and Postal, 2014). However, the result of neg-raising (4) is equivalent to (2). So, at best this response collapses the 3H- puzzle into the 3H-T puzzle. Moreover, the relevant effect also arises if we use ‘it’s not that’, but this form of negation resists neg-raising. ⮭
- This is illustrated by the fact that although (1) is true on Levinson’s account, (4) is false. More generally, it is an elementary property of expected value that can entail and yet the expected value of the latter can be lower than the former by an arbitrary degree. ⮭
- One might want to allow the set of alternatives to vary from world to world, time to time, and agent to agent. One could capture this by maintaining that interpretation proceeds relative to a function from world, time, agent triples to sets of alternatives, rather than just a set of alternatives. But we’ll ignore this complication in what follows. Thanks to an anonymous reviewer for helpful discussion here. ⮭
- We will often drop the world subscript when no confusion will arise. ⮭
- We assume that the set of alternatives always has finite cardinality. ⮭
- As a shorthand, we will write best when we mean . ⮭
- As far as we’re aware, this argument was first put forward by Levinson (2003). It has been endorsed by Lassiter (2011), Jerzak (2019), and Phillips-Brown (2021). ⮭
- We find it plausible that alternatives are at least partly fixed by the subject’s planning and decision-making, and are often tied to the outcomes that are within the subject’s control (see Blumberg and Hawthorne (forthcoming b) for related discussion). Moreover, a reviewer suggests that focus structure could have a role to play in determining which alternatives are relevant (Beaver and Clark, 2008). We are open to this suggestion and plan to explore it in future work. ⮭
- This is at best a helpful model. In reality, irrational agents may have preferences that depart in all sorts of ways from this idealisation (Kahneman and Tversky, 1979), and some rational agents may be out of sync with expected value as well (Buchak, 2013). ⮭
- It is worth registering that we take cases such as Coins to provide stronger motivation for maintaining that the subject’s preference ordering ranges over propositions than cases such as Insurance. This is because insurance cases come with potential confounds, e.g., the subject’s peace of mind from purchasing insurance, that proponents of world-orderings could appeal to in defense of their account (Büring 2003; von Fintel 2012). By contrast, no such moves are available in the Coins scenario. ⮭
- Cf. Cariani’s (2013) notion of a proposition being “visible” with respect to a background partition of logical space. ⮭
- For convenience, we assume that undefinedness or presupposition failure has a semantic effect. But our general approach is compatible with pragmatic accounts of presupposition on which presupposition failure affects assertability rather than semantic value (Schlenker, 2009). ⮭
- This process is usually discussed under the heading “accommodation”. The basic phenomenon goes back at least to Karttunen (1974). See von Fintel (2004) for a more recent discussion. ⮭
- See Quine (1960); Davidson (1984) for canonical discussion of the principle of charity. ⮭
- We will often leave the background ordering over alternatives implicit when discussing dominance, since it is usually clear from context which ranking we mean. ⮭
- See Chierchia and McConnell-Ginet (2000) for discussion. For instance, ‘Mary stopped smoking’ presupposes that Mary smoked in the past, and indeed ‘Mary has not stopped smoking’ carries the very same implication. ⮭
- Note that the felicity of (18) isn’t plausibly explained by appealing to a shift in which alternatives are in play, for example by saying that it is being evaluated relative to the relatively coarse-grained set of alternatives . For we may suppose that the expected value of PASTA is less than or equal to the expected value of CHICKEN. In that case, (18) would be predicted to be undefined/false relative to , but still the sentence has a salient true reading. ⮭
- If the expected value of chicken is greater than the expected value of pasta, then (19) does indeed have a true reading. This can be explained by maintaining that that sentence is being evaluated relative to . ⮭
- A reviewer notes that on this account, ⌜S wants p⌝ can be vacuously true when only contains p-entailing alternatives. However, reports such as ‘Bill wants everyone to be self-identical’ are infelicitous. One could try to explain this by appealing to pragmatic principles on utterance felicity. Alternatively, one could try to capture this constraint semantically by requiring that contains at least one ¬p-entailing alternative (also see fn.35 for related discussion). We remain neutral between these options here. ⮭
- There is a large literature on specific indefinites and how exactly they should be captured. See, e.g., Schwarzschild (2002); Schwarz (2011); Hawthorne and Manley (2012). ⮭
- Assuming that the expected value of getting pasta is less than or equal to the expected value of getting chicken. If this isn’t the case, then a true reading of (22) can be accessed relative to the coarse-grained set of alternatives . ⮭
- Phillips-Brown (2021) has recently argued that subjects can want what isn’t best by their lights. In other work, we discuss how to tweak an alternative-sensitive framework in order to accommodate this phenomenon (Blumberg and Hawthorne, forthcoming c). ⮭
- Note that this prediction marks a significant divergence from existing Kratzerian theories of desire, e.g., the account of von Fintel considered in §2.1. It is straightforward to check that on von Fintel’s account both (23a) and (23b) are predicted to be true. The data in (23) also count against a variant of our proposal which maintains that conditional dominance is a regular entailment rather than a presupposition, as well as a variant which weakens conditional dominance to ‘every such that dominates’. On these versions of the view, both (23a) and (23b) come out true. ⮭
- One way of guaranteeing that alternative sets have the required form is by positing a strengthened representation condition which requires not only that is represented by the background set of alternatives but also that there is some -entailing alternative in , and that there is some -entailing alternative in . ⮭
- Strictly speaking, Gajewski and Križ capture their condition as a homogeneity requirement rather than a presupposition (see Križ (2015, ch.1) for several ways of distinguishing these effects). Moreover, there are differences in how this condition gets spelled out in Gajewski and Križ’s respective systems (see Križ (2015, ch.6) for a helpful comparison of the two approaches). However, these details aren’t important for us here. ⮭
- One area that requires careful investigation is the way our alternative-sensitive approach interacts with quantifiers. Consider a variant of Dinner involving ten people: five diners love spaghetti and hate lasagna; while the other five love lasagna and hate spaghetti. To our ears, ‘Everyone wants spaghetti or lasagna’ improves over its non-quantificational analogue. On the other hand, ‘Everyone wants their friend to order spaghetti or lasagna for them’ seems unacceptable here, which is what our account predicts. At this point, it is unclear what explains this puzzling pattern of judgments. ⮭
- Phillips-Brown (2018) also offers an alternative-sensitive theory of desire reports, but with important differences from our own. First, he places belief constraints on wanting which in §2.1 we showed to be problematic. Second, his account predicts that (8) (‘Bill wants the first coin to land tails, so he wants a result other than three heads’) should be true in Coins. Finally, his account doesn’t explain why (4) (‘Bill wants the first coin to land heads’) is unacceptable, and so doesn’t resolve our puzzles. Also see Blumberg (forthcoming b) for an alternative-sensitive account of natural language preference claims. ⮭
- Of course, the classical approach to deontic modals and desire verbs sees them as sharing an underlying semantics, since it sees both of them as having the force of a universal quantifier. But as we saw in §2.1, that semantics solves neither the 3H-T puzzle nor the puzzle. ⮭
- Also see Blumberg and Hawthorne (forthcoming a). ⮭
- Thanks to two anonymous reviewers at Philosophers’ Imprint and our editor Brian Weatherson for very helpful feedback and discussion. ⮭
References
Beaver David I. and Clark. Brady Z. Sense and Sensitivity: How Focus Determines Meaning. Blackwell, 2008.
Blumberg. Kyle A problem for the ideal worlds account of desire. Analysis, forthcoming a. doi: 10.1093/analys/anab036.10.1093/analys/anab036
Blumberg. Kyle On preferring. Linguistics and Philosophy, forthcoming b.
Blumberg. Kyle and Hawthorne. John Inheritance: Professor procrastinate and the logic of obligation. Philosophy and Phenomenological Research, forthcoming a. doi: 10.1111/phpr.12846.10.1111/phpr.12846
Blumberg Kyle and Hawthorne. John A new hope. Journal of Philosophy, forthcoming b.
Blumberg Kyle and Hawthorne. John Wanting what’s not best. Philosophical Studies, forthcoming c.
Buchak. Lara Risk and Rationality. Oxford University Press, 2013.
Büring. Daniel To want is to want to be there: A note on Levinson (2003). In Schlenker Philippe and Sportiche, Dominique editors, Division of Linguistic Labor: The la Bretesche Workshop, 2003.
Cariani. Fabrizio ‘Ought’ and resolution semantics. Noûs, 47(3):534–558, 2013. doi: 10.1111/j.1468-0068.2011.00839.x.10.1111/j.1468-0068.2011.00839.x
Chierchia Gennaro and McConnell-Ginet. Sally Meaning and Grammar: An Introduction to Semantics. MIT Press, 2000.
Collins Chris and Postal. Paul M. Classical NEG Raising: An Essay on the Syntax of Negation. MIT Press, 2014.
Crnič. Luka Getting even. PhD thesis, MIT, 2011.
Davidson. Donald Inquiries Into Truth And Interpretation. Oxford University Press, 1984.
Dorr Cian and Hawthorne. John Embedding epistemic modals. Mind, 122(488):867–914, 2013. doi: 10.1093/mind/fzt091.10.1093/mind/fzt091
von Fintel. Kai NPI Licensing, Strawson entailment, and context dependency. Journal of Semantics, 16(2):97–148, 1999. doi: 10.1093/jos/16.2.97.10.1093/jos/16.2.97
von Fintel. Kai Would you believe it? The king of France is back! (Presuppositions and truth-value intuitions). In Reimer Marga and Bezuidenhout, Anne editors, Descriptions and Beyond. Clarendon Press, 2004.
von Fintel. Kai The best we can (expect to) get? Challenges to the classic semantics for deontic modals. Central APA, 2012.
Robert Gajewski. Jon Neg-raising and polarity. Linguistics and Philosophy, 30(3):289–328, 2007. doi: 10.1007/s10988-007-9020-z.10.1007/s10988-007-9020-z
Grano Thomas and Phillips-Brown. Milo (Counter)factual want ascriptions and conditional belief. MIT, 2022.
Hawthorne John and Manley. David The Reference Book. Oxford University Press, 2012.
Heim. Irene Presupposition projection and the semantics of attitude verbs. Journal of Semantics, 9(3):183–221, 1992.
Hintikka. Jaakko Knowledge and Belief: An Introduction to the Logic of the Two Notions. Cornell University Press, 1962.
Iatridou. Sabine The grammatical ingredients of counterfactuality. Linguistic Inquiry, 31(2):231–270, 2000. doi: 10.1162/002438900554352.10.1162/002438900554352
Jackson Frank and Pargetter. Robert Oughts, options, and actualism. Philosophical Review, 95(2):233–255, 1986. doi: 10.2307/2185591.10.2307/2185591
Jeffrey. Richard C. The Logic of Decision. University of Chicago Press, 1965.
Jerzak. Ethan Two ways to want? Journal of Philosophy, 116(2):65–98, 2019. doi: 10.5840/jphil201911624.10.5840/jphil201911624
Kahneman Daniel and Tversky. Amos Prospect theory: An analysis of decision under risk. Econometrica, 47(2):263–291, 1979.
Karttunen. Lauri Presupposition and linguistic context. Theoretical Linguistics, 34(1):181–194, 1974.
Manuel Križ. Aspects of Homogeneity in the Semantics of Natural Language. PhD thesis, University of Vienna, 2015.
Lassiter. Daniel Measurement and Modality: The Scalar Basis of Modal Semantics. PhD thesis, New York University, 2011.
Levinson. Dmitry Probabilistic model-theoretic semantics for ‘want’. Semantics and Linguistic Theory, 13:222–239, 2003. doi: 10.3765/salt.v13i0.2888.10.3765/salt.v13i0.2888
Lewis. David K. Counterfactuals. Blackwell, 1973.
Pasternak. Robert A lot of hatred and a ton of desire: Intensity in the mereology of mental states. Linguistics and Philosophy, 42(3):267–316, 2019. doi: 10.1007/s10988-018-9247-x.10.1007/s10988-018-9247-x
Phillips-Brown. Milo I want to, but... Proceedings of Sinn und Bedeutung, 21:951–968, 2018.
Phillips-Brown. Milo What does decision theory have to do with wanting? Mind, 130(518):413–437, 2021. doi: 10.1093/mind/fzaa057.10.1093/mind/fzaa057
Portner Paul and Rubinstein. Aynat Mood and contextual commitment. In Chereches, Anca editor, Semantics and Linguistic Theory, volume 22, 2012. doi: doi:10.3765/salt.v22i0.2642.10.3765/salt.v22i0.2642
Van Orman Quine. Willard Word and Object. MIT Press, 1960.
Rubinstein. Aynat Roots of Modality. PhD thesis, University of Massachusetts Amherst, 2012.
Scheffler. Tatjana Semantic Operators in Different Dimensions. PhD thesis, University of Pennsylvania, 2008.
Schlenker. Philippe Local contexts. Semantics and Pragmatics, 2(3):1–78, 2009. doi: 10.3765/sp.2.3.10.3765/sp.2.3
Schwarz. Bernhard Long distance indefinites and choice functions. Language and Linguistics Compass, 5(12):880–897, 2011. doi: 10.1111/j.1749-818X.2011.00315.x.10.1111/j.1749-818X.2011.00315.x
Schwarzschild. Roger Singleton indefinites. Journal of Semantics, 19(3): 289–314, 2002. doi: 10.1093/jos/19.3.289.10.1093/jos/19.3.289
Stalnaker. Robert Inquiry. Cambridge University Press, 1984.