Kant on Decomposing Synthesis and the Intuition of Infinite Space

1. A puzzle about Kant’s account of the intuition of space

In the Transcendental Aesthetic of the Critique of Pure Reason, Immanuel Kant claims that our representation of space is a priori, i.e. not acquired from experience (A23/B38).¹ Moreover, he argues that this representation is an intuition rather than a concept and that it presents an ‘infinite given magnitude’ (A25/B39). He then concludes from this that space is ‘ideal’ (A28/B44), i.e. a mere ‘subjective condition of sensibility’ (A26/B42) or ‘form of our sensibility’ (A21/B35). Later on, in the Transcendental Analytic, he introduces a further requirement on our ability to represent space. In § 26 of the second edition of the Critique, Kant writes:

space and time are represented a priori not merely as forms of sensible intuition, but also as intuitions themselves (which contain a manifold), and thus with the determination of the unity of this manifold in them (see the Transcendental Aesthetic).* Thus even unity of the synthesis of the manifold, outside or within us, hence also a combination with which everything that is to be represented as determined in space or time must agree, is already given a priori, along with (not in) these intuitions. (B160–1)²

In a footnote to this passage, Kant explains that in the Aesthetic he had ascribed the unity of the intuition of space ‘merely to sensibility, only in order to note that it precedes all concepts’ (B160–1fn.). However, he then adds, this unity nevertheless ‘presupposes a synthesis which does not belong to the senses’ and through which ‘space and time are first given as intuitions’ (ibid.). Kant calls the preconceptual synthetic activity that is required for the intuition of space ‘figurative [synthesis] (synthesis speciosa)’ (B151) and describes it as an activity that the understanding ‘exercises under the designation of a transcendental synthesis of the imagination’ (B153f.; see also B162fn.). This synthesis of the imagination is preconceptual insofar as the representations on which it operates, and also those which it generates, are always intuitions (B151).³ Yet it also involves the spontaneity of the understanding since the resulting intuitions are not generated by sensibility alone, which is a purely passive faculty, but are rather produced spontaneously.

Kant’s reason for assuming that a synthesis of the imagination is a necessary ingredient of the pure intuition of space seems to be the following: In both versions of the first Critique, Kant introduces synthesis as a mental activity that is necessary for our becoming aware of sensible manifolds as such, i.e. as containing either a plurality of features (like different shapes or colors) or a plurality of parts (like spatial or temporal parts). Although such a manifold might be given to us ‘at one blow’ in some sense, becoming aware of it as a manifold is possible only if we attend to the different aspects one after the other, ‘for as contained in one moment no representation can ever be anything other than absolute unity. Now in order for this manifold to turn into unity of intuition (as, say in the representation of space), it is necessary first to run through and then take together this manifoldness’ (A99). Kant continues to argue that attending to one part after the other alone is not enough in order to generate an awareness of the manifold of these parts as such:

Now it is obvious that if I draw a line in thought, or think of the time from one noon to the next […], I must necessarily first grasp one of these manifold representations after another in my thoughts. But if I were always to lose the preceding representations (the first parts of the line, the preceding parts of time […]) from my thoughts and not reproduce them when I proceed to the following ones, then no whole representation […], not even the purest and most fundamental representations of space and time, could ever arise. (A102)

On a straightforward reading, the quoted passages imply that the pure intuition of space entails or presupposes a synthetic activity because this intuition involves an awareness of a spatial manifold as such.⁴

Several authors have recently pointed out that the straightforward reading is confronted with at least two severe problems.⁵ The first problem can be dubbed the problem of the finiteness of synthesis. Synthesis is an activity performed by finite human minds. If we conceive of it as a process of ‘running through’ and ‘taking together’ a manifold of features, or parts, which enables an awareness of this manifold as such, then, regardless of the precise nature of this process, it seems clear that the manifold brought to awareness by this process can only be finitely large. For how could a finite mind ‘run through’ infinitely many parts or features? However, space is an ‘infinite given magnitude’, i.e. it is infinitely large. So, if any intuition of a spatial manifold really presupposes a synthesis, then it seems unclear how Kant can allow there to be an intuition of infinite space.

The second problem can be called the problem of the priority of the whole. Acts of synthesis seem to have a structure in which the representation of the parts is prior to that of the whole. If we take Kant’s example of the ‘drawing of a line in thought’, this drawing of the line consists in first running through the different segments of the line and then combining them in an intuition of the whole line as consisting of these segments. However, Kant makes clear that our intuition of infinite space does not have this parts-prior-to-their-whole structure, but rather a whole-prior-to-its-parts structure. When he argues in the Transcendental Aesthetic that our representation of space is an intuition rather than a concept, he writes:

one can only represent a single space [einen einigen Raum], and if one speaks of many spaces, one understands by that only parts of one and the same unique space [eines und desselben alleinigen Raums]. And these parts cannot as it were precede the single all-encompassing space [dem einigen allbefassenden Raume] as its components […], but rather are only thought in it. It is essentially single; the manifold in it […] rests merely on limitations. (A25/B39)⁶

Kant is as explicit as one can be here: Our representation of the one infinite space does not result from a preceding awareness and combination of all of its finite parts. On the contrary, any awareness of finite regions of space presupposes a representation of infinite space, for these regions can only be given to us as limitations of infinite space. But how can Kant assume then that the presentation of infinite space presupposes a synthesis?

Over the last years a number of proposals have been made as to how the two problems with Kant’s claims about the connection between synthesis and the intuition of space can be solved. A first strategy is to assume that Kant took synthesis not to be a precondition of the unity of space itself, but rather only of the unity of particular determinate and finite spatial regions and objects (e.g. the unity that the parts of a line have by all belonging to one circle).⁷ However, this assumption does not really fit the textual evidence. As we have just seen, Kant claims that without synthesis ‘not even the purest and most fundamental representations of space and time could ever arise’ (A102; see also A99–100). Moreover, he says that in the Transcendental Aesthetic, he had ‘ascribed this unity merely to sensibility, only in order to note that it precedes all concepts’ (B160fn.). But the only unity (‘Einheit’) mentioned in the Transcendental Aesthetic is the unity of the whole of space mentioned in the above quote from A25/B39.

A second strategy consists in assuming that synthesis is not a condition of the unity of space as an object of intuition, but rather only for the unity that space has as the object of a representational state that is somehow cognitively more demanding than intuition.⁸ Onof and Schulting (2015), for example, think that synthesis is only a precondition of ‘the grasp of the unicity of space by the faculty of understanding’ (27). I cannot discuss the details of Onof and Schulting’s very detailed and careful interpretation here.⁹ I only want to confess again that I find it difficult to reconcile it with Kant’s explicit statement that it is through synthesis that ‘space or time are first given as intuitions’ (B161fn.) and that without it ‘not even the purest and most fundamental representations of space and time could ever arise’ (A102; emphasis mine). In Kant’s terminology, ‘given in intuition’ contrasts with ‘thought/grasped by the understanding’, and the most fundamental representation of space clearly is the intuition of space and not some cognitively more demanding representation of it.

A third strategy accepts that synthesis is a requirement on the intuition of space and its unity but assumes that the required synthesis is not the figurative synthesis of the imagination, but rather a second form of synthesis whose nature is not in conflict with the infinity and whole-prior-to-its-parts structure of space. This idea has been put forward most explicitly by Williams (2018),¹⁰ who thinks that the synthesis responsible for the unity of space is not the category-guided synthesis that brings about the unity of particular spatial regions and objects, but rather an ‘original synthesis’, which she describes as a form of self-consciousness: ‘[I]t is through the subject’s consciousness of her own capacity to determine her sensible nature that the pure manifolds of space and time are given to the subject as singular wholes’ (ibid., 13).¹¹ Williams’s idea seems to be that the thinking subject is conscious of her own identity through all of her experience and hence also has an awareness that all parts of the spatio-temporal manifold have unity insofar as they all belong to herself and are further determinable by her. Now, although I think that Williams is right to point out the essential connection between the singularity of space and time and the identity of the subject of experience, I am skeptical that she manages to show that it is just the awareness of the identity of the subject with respect to the spatio-temporal manifold that constitutes the singularity of space and time. For assume per impossibile that space and time were not singular wholes and that there was nothing but a manifold of unconnected times and spaces. And assume further — maybe also per impossibile — that a subject experiencing these different times and spaces was aware of her own identity and capacity to determine them. That might give unity to these spaces and times in the sense that they are all experienced by the same subject. But without further argument, it is hard to see why this by itself would make them parts of one singular space or time.¹²

Although I am aware that these objections against existing interpretations are too superficial to be conclusive, I hope that they at least make it reasonable to look for an alternative. This is what I want to do in the present paper. My proposal will be based on the denial of an assumption that is shared by all previous solutions to the puzzle, namely the assumption that the figurative synthesis of the imagination always has a compositional parts-prior-to-their-whole structure. The key element of my interpretation will be a passage in which Kant explicitly asserts that there is not only a ‘composing’ but also a ‘decomposing’ synthesis, i.e. an activity of the imagination by which we divide a previously given whole.¹³ Although Kant’s remarks about decomposing synthesis do not appear in the context of his claims about synthesis and the intuition of space, which is probably the reason why they have hitherto been ignored by all participants of the debate, I will argue that it is just this kind of decomposing synthesis that brings about our intuition of infinite space: We representationally decompose infinite space into one of its finite segments and the remaining infinite region excluded by that segment, and this activity makes us perceptually aware not only of the finite segment but also of the unlimited space that is the background, or horizon, from which it is carved out.

I will proceed as follows. In the next section, I will introduce Kant’s notion of decomposing synthesis and explain why it makes perfectly good sense for Kant to assume that there is not only composing but also decomposing synthesis. In Section 3, I will then explain how the notion can be applied to the case of a decomposition of infinite space, and I will show that there is good textual evidence that the decomposition model indeed corresponds to the way in which Kant thought we intuit infinite space. Decomposing synthesis will turn out to be the activity which Kant in the Transcendental Aesthetic calls ‘limitation’. Section 4 will offer solutions to the two problems mentioned in this introduction. I will explain how the decomposition model allows finite minds to intuit the infinite and how it can do justice to the whole-prior-to-its-parts structure of space. I will further argue that the model is also attractive from a non-exegetical point of view and can answer the question of what the perceptual content of the intuition of infinite space is in a more plausible way than rival accounts. Section 5 situates the proposed interpretation within the spectrum of conceptual-ist and non-conceptualist interpretations of Kant’s account of the pure intuition of space. In Section 6, I will show how the proposal accounts for the particular kind of unity that Kant assigns to space in § 26 and argue that it meshes nicely with the role this unity plays for the argument of Kant’s Transcendental Deduction. Section 7 concludes.

2. Decomposing synthesis

In the course of his solution to the Second Antinomy, Kant claims that the two conflicting assumptions at issue — that matter consists of simple parts and that matter does not consist of simple parts — both rest on the false presupposition that the parts of a given appearance exist and have a determinate number prior to the process through which they are given to us as parts in experience. Kant holds that this assumption is false. Although an appearance like a certain portion of matter consists of infinitely many ‘possible parts’ (A513–4/B541–2), these parts do not actually exist before they are given to us in experience. He writes:

[I]t is by no means permitted to say of such a whole, which is divisible to infinity, that it consists of infinitely many parts. For though all the parts are contained in the intuition of the whole, the whole division is not contained in it; this division consists only in the progressive decomposition, or in the regress itself, which first makes the series actual. (A524/B552)

Hence I will have to say: the multiplicity of parts in a given appearance is in itself neither finite nor infinite, because appearance is nothing existing in itself, and the parts are given for the very first time through the regress of the decomposing synthesis [‘durch den Regressus der decomponirenden Synthesis’], and in this regress, which is never given absolutely wholly either as finite nor as infinite. (A505/B533)¹⁴

These claims are very controversial, of course, and a lot would need to be said in order to make intelligible how they could be the basis of a plausible solution to the Second Antinomy. However, the solution to the antinomy is not our concern here. I have only alluded to the passages because they contain Kant’s most explicit statement about a particular mental process through which the parts of a given extended magnitude become objects of our awareness, i.e. are given to us as parts of a whole. In the first quote, Kant calls this process ‘decomposition’; in the second quote, he speaks of it as a ‘decomposing synthesis’.

Now, one might think that the latter expression contains a contradiction in terms.¹⁵ Synthesis is an activity by which a manifold of items is ‘brought together’ into a whole. Decomposition is a process by which a whole is divided into manifold parts. How could there ever be such a thing as a ‘decomposing synthesis’? The paradoxical nature of the expression disappears, however, once we take into account that Kant does not introduce synthesis as a requirement for bringing about manifolds simpliciter, but rather as one for bringing about manifolds as objects of our awareness.¹⁶ Although there are interpretations that read Kant as holding a form of representational atomism, according to which no non-simple items could ever be given to us in sensibility and any sensible manifold would have to be composed from atomic elements,¹⁷ it is neither compulsory nor plausible to take Kant to be committed to such a form of atomism.¹⁸ I will follow Grüne (2009) in assuming (i) that the function of sensible synthesis is to make sensible manifolds conscious as such, (ii) that this consciousness consists in the clarity and distinctness of the representations we have of those manifolds, and (iii) that the degree of clarity and distinctness of our representations depends on our abilities to discriminate among them in a way that does not yet include the application of concepts in judgements. Given this understanding of the function of synthesis, Kant can accept that mereological pluralities are provided by our sensibility prior to any process of synthesis in some sense.¹⁹ In fact, he agrees that space as a form of our intuition, which contains such a mereo-logical plurality, exists independently of any synthesis (B160–1). What he wants to deny is that mereological pluralities could ever be objects of our awareness through our passive sensibility alone. In order for us to intuit mereological pluralities as wholes consisting of parts, or the manifold parts as being the parts of one whole, it is not enough that these pluralities are somehow given to our senses, but we also need to be able to sensibly discriminate and combine their parts. It is this sensible discrimination and combination that requires synthesis.²⁰

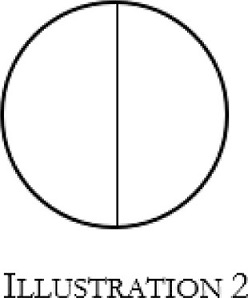
Once we accept that mereological pluralities can be given to us prior to any synthesis in some sense, we can see that there are two ways of becoming aware of mereological pluralities as such. According to the first way, a manifold of parts is first ‘run through’, i.e. given to the subject one after the other, and then somehow combined in a representation of these parts as all belonging to one whole. Examples of such a synthesis by combination, or composition, are cases of empirical intuitions of complex objects (like the doorway of a Gothic church, say) or cases of pure intuitions of geometrical figures (like Kant’s ‘drawing of a line in thought’). However, there can also be synthesis by decomposition, i.e. the becoming aware of parts as parts of a whole through the division of a given whole. We can see this by means of the following two illustrations, which show an area circumscribed by a circle, i.e. a disk, before and after its division into two halves by a line:

Let us call the two halves into which the line divides the disk in Illustration 2 ‘A’ and ‘B’. It is clear that in some sense, A and B are already present, or ‘given’, in Illustration 1. After all, A and B are spatial regions included by the circle. Like infinitely many other regions they are what Kant would have called ‘possible parts’ of the disk (A513–4/B541–2).²¹ However, it is also clear that there is another sense in which A and B are represented only in Illustration 2. Only here are A and B distinguished from each other and picked out from, or made salient among, all the other infinitely many possible parts of the disk. If we identify what is shown by the two illustrations with the perceptual content of a subject who is intuiting the disk, we can say that only the content associated with Illustration 2 provides the subject with an awareness of the manifold consisting of A and B as such, or with an awareness of the disk as having these two parts. If synthesis is the activity through which we become aware of a sensible manifold as such, or of a whole as consisting of parts, we can now see how there can be such a thing as a decomposing synthesis. For what generated the awareness of A and B was not a process of first ‘running through’ A and B one after the other and then combining them in a representation of the whole that consists of them. It was rather a process of dividing, or decomposing, a given whole into parts through which these parts were given to us as parts. Decomposing synthesis allows us to distinguish the two parts from each other as well as distinguish them from the whole that they compose.²²

We should note, though, that the decomposing synthesis also involves a composing synthesis. The drawing of the line that divides the circle is an act of composing synthesis, and even if we did not draw this line ourselves but just perceived it, Kant thought that we would have to run through a manifold of line segments in order to become aware of the line as consisting of this manifold. So by drawing the line we perform two acts of synthesis at the same time: an act of combining the segments of the line into one whole line, which makes us aware of the segments as all belonging to one whole line, and the act of dividing the whole disk into two halves, which makes us aware of the whole disk as consisting of two parts.

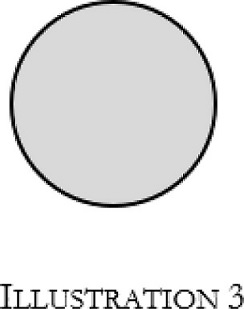
I next want to point to another case of decomposing synthesis, which is special in a certain respect and will be essential for my account of an intuition of infinite space. In the case of the division of the circle by a line, what is decomposed is a determinate spatial figure, one whose boundaries are part of the content of the respective intuition. Let us call such a case the decomposition of a phenomenally limited whole. There are also cases of decomposing synthesis that are decompositions of a phenomenally unlimited whole, i.e. a whole that either has no boundaries at all or whose boundaries are at least not phenomenally present to us. Let us have a second look at what happens when we draw the (undivided) circle in Illustration 1. According to Kant, we perform an act of composing synthesis by which we become aware of the different line segments as all belonging to one circle. However, we again also perform an act of decomposing synthesis. For by drawing the line of the circle, we distinguish the area within the boundaries of the circle from the area outside of it, and we do so by dividing, or decomposing, the area that is the mereological sum of them. We can make this more vivid by coloring the former in grey:

Now unlike in the case of the division of the disk in two halves, in this case neither the region that we have decomposed nor the region which we have separated from the disk by drawing the line of the circle are determinate spatial figures. What we have divided is a phenomenally unlimited whole, namely the (white) background into which we began to draw the circle. And when we have divided this phenomenally unlimited whole into a determinate spatial region (the grey area within the circle) and the rest (the remaining white area outside the circle), this latter region is again phenomenally unlimited. Of course, we could also have drawn the circle into a limited whole such as another, larger area, and one might argue that the circle shown in Illustration 3 in fact divides such a limited larger whole, namely the surface of a piece of paper. However, there are certainly cases in which the whole from which the determinate figure is distinguished is actually phenomenally unlimited, for example when we draw the circle on a white wall that fills all of our visual field, or when we do geometrical constructions in pure intuition. Borrowing a term from Edmund Husserl, I will call a phenomenally unlimited background from which a determinate spatial object is distinguished, when presented to the mind, the phenomenal horizon in which the determinate spatial object appears.²³

So we can conclude that acts of decomposing synthesis sometimes divide a whole into a limited spatial figure and the unlimited phenomenal horizon in which it is presented. As in the case of the division of the disk, this act of decomposing synthesis is at the same time an act of composing synthesis (the drawing of a line), but again it is the act of decomposition that generates an awareness of the two parts as being distinguished from each other and as being distinct from the whole which they compose.

3. Decomposing infinite space

I think that the notion of a decomposing synthesis is the key to understanding why Kant thought that an activity of synthesis is required, as well as suited, to provide us with an intuition of infinite space. What I want to suggest is (i) that infinite space is given to us in intuition by decomposing it into a finite segment and an unlimited phenomenal horizon within which the finite segment presents itself and (ii) that we are aware of the infinity of space by being aware that any other finite segment that we could ever intuit will always present itself within this unlimited phenomenal horizon.

In order to defend these two claims I first want to point to two passages before the footnote in § 26, in which Kant explains in more detail why and in what sense a spontaneous activity of the imagination is an essential part of the generation of a priori intuitions of space and time. In § 24, Kant writes that inner sense alone contains:

the mere form of intuition, but without combination of the manifold in it, and thus […] does not yet contain any determinate intuition at all, which is possible only through the consciousness of the determination of the manifold through the transcendental act of the imagination (synthetic influence of the understanding on the inner sense), which I have named the figurative synthesis. (B154)

He then provides the following more concrete model of what the imagination does when we intuit space:

We can always perceive this in ourselves. We cannot think of a line without drawing it in thought, we cannot think of a circle without describing it, we cannot represent the three dimensions of space at all without placing three lines perpendicular to each other from the same point [aus dem selben Punkte zu setzen]. (B154)²⁴

The acts mentioned in the passage are all acts of drawing lines by moving a point in order to construct the three-dimensional Euclidian space and geometrical figures within it. We should note that these movements of points are not the physical movements that we perform when we do compass-and-straightedge constructions, but rather their mental analogues. Kant calls them ‘motion[s], as act[s] of the subject’ and distinguishes them from motions ‘as determination[s] of an object’ (B155). In a footnote, he explains this distinction as follows:

Motion of an object in space does not belong in a pure science, thus also not in geometry; for that something is movable cannot be cognized a priori but only through experience. But motion, as description of a space, is a pure act of the successive synthesis of the manifold in outer intuition in general through productive imagination, and belongs not only to geometry but even to transcendental philosophy. (B155fn.)

The end of this passage makes clear that motions, understood as the mental acts of drawing lines in our imagination, not only are required to do geometry but are also a condition of the possibility of experience in general. It is plausible to assume that the reason for this claim is that we have to perform these acts in order to intuit extensive magnitudes in general and space in particular, which — as Kant shows later in the Axioms of Intuition²⁵ — in turn is a condition of experiencing objects.

Let us now move on to the question of how these motions in the imagination can provide us with an intuition of infinite space. For reasons of presentations, I will confine myself to the case of an intuition of an infinite two-dimensional space, but it should be obvious how my solution can be applied to the pure intuition of an infinite three-dimensional space. Following Kant’s own suggestion in the penultimate quotation, I will assume that this space can be given to us in pure intuition by drawing in our imagination two perpendicular lines from the same point and, by doing so, constructing a finite geometrical space between them (Illustration 4).

As Kant writes in the previous quotation, drawing the lines from A to B and from A to C consists in acts of ‘successive synthesis of the manifold in outer intuition’, i.e. it is a case of what I have called ‘composing synthesis’, in which we first run through the parts of a whole (the line segments that we produce by drawing the line) and, on this basis, form an intuitive representation of the whole (the whole line). However, the drawing of the lines is also a case of the second form of decomposing synthesis that I have introduced above. It is a case of a decomposition of an indeterminate and unlimited whole into a limited determinate part — the two lines and the space in between them — and an unlimited phenomenal horizon. When I draw the lines from A to B and from A to C in my imagination, what is phenomenally present to me is not only the lines themselves but also the space into which the lines are drawn. There is space below A and above B and left of A and right of C. And not only is there this space; it is also phenomenally present in the intuition we have of the two drawn lines, namely as the phenomenal horizon, or background, in which the lines are given to us. The same holds for the two-dimensional geometrical space that is spanned by drawing the two perpendicular lines (the grey area in Illustration 4). When we draw the lines, it is not only this limited two-dimensional space that is intuitively given to us but also the unlimited two-dimensional space into which it is placed (which is white in the illustration). So it seems correct to say that by drawing the lines, we are presented not only with the lines and the space spanned by them but also with the unlimited two-dimensional phenomenal horizon in which these determinate figures appear and also with the unlimited whole that has the determinate figures and their unlimited horizon as its parts. And it seems equally correct to say that without drawing the lines, we would not be phenomenally aware of either this unlimited whole or of its limited or unlimited parts. So, two-dimensional space is given to us in intuition by decomposing it into a finite segment and an unlimited horizon.

The proposed model of how space is phenomenally present to us in intuition fits very smoothly with what Kant says about our intuition of space in the Transcendental Aesthetic. In his first argument for the apriority of space, Kant claims that our representation of space could not be acquired empirically by abstracting it from perceiving particular spatial objects and relations. His reason for this claim is that ‘in order for certain representations to be related to something outside me (i.e., to something in another place in space from that in which I find myself), thus in order for me to represent them as outside one another, thus not merely as different but in different places, the representation of space must always be their ground’ (A3/B38). Daniel Warren has convincingly argued that we should understand this consideration as being based on the phenomenological insight that we cannot represent any finite and determinate spatial objects, or relations, without representing them as being part of space.²⁶ In the case of our Illustration 4, Kant’s point would be that we can never just intuit points A, B, and C and the relation between them. Intuiting these three points implies intuiting a fourth thing, namely the space in which they are placed.²⁷ It is phenomenally impossible just to represent objects but not the space around them.²⁸

My proposal is also supported by Kant’s first argument that our representation of space is an intuition rather than a concept, from which I have already quoted above. Kant claims here that any manifold of different spaces is a manifold of parts of one single space and that these parts do not ‘precede’ this one single space as components from which the latter is constructed, but rather ‘rest merely on limitations’ (A25/B39). Analogously, in the Inaugural Dissertation, he says that ‘it is only when both infinite space and infinite time are given that any definite space and time can be specified by limiting’ (2:405). I think that what Kant calls ‘limitation’ here is exactly what I have introduced as ‘decomposition’. ‘Limitation’ could of course mean the act of setting limits to a finite spatial magnitude, e.g. by marking the endpoints of a line. But this is clearly not what Kant has in mind in his remarks. The limitation through which all finite spatial regions are given is not the limitation of these finite regions, but the limitation of the ‘single all-encompassing space’ (A25/B39). This space is limited by carving finite segments, or parts, out from it. This is exactly what I have called decomposition.²⁹

So let us take it that infinite space is given to us as an object of consciousness via a process in which we decompose it into (i) a limited region and (ii) the phenomenal horizon of this region. In the next section we will see that this model allows us to solve the puzzle men tioned in Section 1.

4. Solving the puzzle

The first problem, the problem of the finiteness of synthesis, consisted in the lack of an explanation how finite minds can have an intuition of something infinite. In order to see how the present proposal can solve it, we have to explain why our phenomenal awareness of the unlimited phenomenal horizon in which all finite spatial figures appear can be interpreted as an awareness of infinite space. This assumption is by no means trivial, because the phenomenal horizon in which the spatial figures drawn in our imagination present themselves is not infinitely large. It does not present itself as having boundaries, but that means neither that it presents itself as being infinite nor that it is infinite.

In order to solve this problem, we should first note that to say that an entity x, which has a certain feature F, is given to us in intuition is not the same as to say that x and its F-ness are given to us in intuition. We can see stars that are one million light-years away from us without seeing their distance from us. We can see a liquid with a certain chemical constitution without seeing its chemical constitution. We can have a pure intuition of a triangle whose angular sum is 180° without intuiting its angular sum by that alone, etc. So, to claim that infinite space is given to us in intuition does not mean that its infinity is given to us in intuition or that we immediately see its infinity.³⁰ Hence, a first step to a solution to the problem is to acknowledge that we simply do not have to assume that the phenomenal horizon in which finite spatial objects and regions appear has a phenomenal character that marks it as being infinitely large. Note that this does not mean that the phenomenal character of the phenomenal horizon does not play any role for its presenting us with infinite space. For if the horizon in which a determinate and finite object appears presented itself as limited instead of unbounded (like the sheet of paper on which we draw a circle), then representing an object within such a horizon would certainly not count as presenting it as part of infinite space. However, this still does not give us positive reason to think that we do so by representing it within an unbounded horizon.

This positive reason comes from a second feature of the phenomenal horizon, one that is not immediately present through its phenomenal character, but only reveals itself through a certain procedure that we could call ‘free variation in our imagination’ — again borrowing a term from Husserl.³¹ In the present case, this procedure consists in imaginatively extending the previously drawn lines, by which we have constructed the finite space that appears in the horizon. The free variation of the lengths of the lines reveals to us that however large the finite space that we construct by drawing the lines is, this space will always only be phenomenally present to us within the horizon of a still larger unlimited space.³² Any finite space, however large it may be, can only be the object of our intuition through the limitation, or decomposition, of a still larger and phenomenally unlimited space. I think there are very good reasons to assume that it is nothing but this fact about space that Kant means when he claims that space is an ‘infinite given magnitude’.³³

The first reason is a passage from Kant’s unpublished remarks On Kästner’s Treatise,³⁴ in which he explains how the infinitude of the originally given ‘metaphysical space’ is to be distinguished from the infinitude of the geometrical space, or rather spaces, with which geometry is concerned. By a ‘geometrical space’, Kant means the space that is constructed by drawing lines in our imagination. The space constructed by drawing lines from point A to points B and C in the above Illustration 4 would be such a geometrical space. Kant points out that geometrical spaces are never actually infinite, but only potentially infinite: every constructed geometrical space is such that a larger geometrical space could be constructed, but it would itself be finite (cf. 20:420). However, Kant points out an important distinction between the potential infinity of geometrical spaces and the potential infinity of natural numbers:³⁵

Now when the geometer says that a line could always be extended no matter how far one has drawn it, then this does not mean what is said in arithmetic about numbers, namely that one can always, and endlessly, increase them through the addition of other units or numbers (for the added numbers and magnitudes, which are expressed through it, are for themselves possible, without them having to belong, together with the previous ones, as parts, to one magnitude); rather, that a line can be extended to infinity means so much as: the space in which I describe the line, is greater than every one line which I may describe in it; and thus the geometer grounds the possibility of his task of increasing a space (of which there are many) to infinity on the original representation of a unitary, infinite, subjectively given space. (AA 20:419–20)

Applied to our distinction between composing and decomposing syntheses we can summarize Kant’s point in this passage as follows: Numbers and geometrical spaces are both products of acts of composing synthesis. Since the result of such acts is always only finitely large, there are only potentially-infinitely many numbers and potentially-infinitely large geometrical spaces. However, unlike numbers, which are not the result of carving out a part from a previously given magnitude, geometrical spaces are always also the products of a decomposing synthesis. They are the products of a decomposition, or limitation, of a still larger space:

In [metaphysics, space] is original and only one (unitary) space, in [geometry, space] is derived and hence there are (many) spaces, of which the geometer however, in accord with the metaphysician, must admit as a consequence of the foundational representation of space, that they can only be thought as parts of the unitary original space. Now one cannot name a magnitude, in comparison with which each assignable [unit] of the same type is only equal to a part of it, anything other than infinite. Thus, the geometer, as well as the metaphysician, represents the original space as infinite, in fact as infinitely given. (20:419)

Note that Kant says not only that the metaphysical space, which is presupposed by any geometrical construction, is actually infinite but also that it is ‘given as infinite’. This means, I suggest, that it is given as the space from which any finite geometrical space is carved out in an act of decomposing synthesis.³⁶

This understanding of the infinity of metaphysical space also corresponds nicely to Kant’s characterization of the infinity of time in the Transcendental Aesthetic. ‘The infinity of time,’ he writes, ‘means nothing more than that every determinate magnitude of time is only possible through limitations of a single time grounding it. The original representation time must therefore be given as unlimited’ (A32/B47–8).³⁷

Last but not least, our interpretation is supported by what Kant says about the ‘true’ understanding of infinity in the Critique of Pure Reason:

The true (transcendental) concept of infinity is: that the successive synthesis of the unit [‘die sukzessive Synthesis der Einheit’] in the traversal of a quantum can never be completed. This [quantum] thereby contains a multitude (of the given unit [‘Einheit’]) that is greater than any number which is the mathematical notion of the infinite. (A432/B460)³⁸

Here Kant connects his conception of synthesis with his theory of measurement. We measure a given quantum by successively adding instances of a given unit and by counting these instances. A quantum is infinite if the process of its measurement cannot be completed. Metaphysical space is infinite in this sense because any procedure of measurement, which is a case of compositional synthesis, always presupposes the one all-encompassing space which is decomposed into the measured quantum and the horizon within which it appears.

Let us next come to our second problem, the problem that the representation of infinite whole of space is in some sense prior to that of any finite spatial region. It should be clear that this fact is no longer incompatible with the assumption that the intuition of space presupposes an act of synthesis once we accept that there is not only composing but also decomposing synthesis. For whereas acts of composing synthesis presuppose that we first grasp the parts in order to combine them into a whole, acts of decomposing synthesis do not have this parts-prior-to-their-whole structure. Here, the parts are only given to our awareness as the result of synthesis. It is important not to misunderstand the claim that space is prior to its parts as saying that we could first have an intuition of infinite space and then decompose it into finite segments and a phenomenal horizon, which would indeed be very implausible. However, Kant is not committed to such a view. He can accept that space as an object of intuition is only given as the phenomenal horizon of some object in space from which we distinguish it. In fact, his claim that ‘a synthesis which does not belong to the senses’ is required for ‘space and time [to be] first given as intuitions’ (B160–1fn.) can be understood precisely as the affirmation that without the distinction between the horizon and the object that appears in it, which is brought about by decomposition, no sensible consciousness of space would be possible.

This result fits well with Kant’s general views about consciousness. As I have mentioned above, Kant assumed that whether and to what degree the representation of a certain object is conscious depends on whether and to what degree this representation enables us to distinguish the object from other objects. For example, Kant thought that when we look at the Milky Way, we have sensible representations of all the stars that constitute it, but these sensible representations are non-conscious because they do not enable us to distinguish the different stars from one another.³⁹ Something similar could be said about cases of pure intuition like that of the circle in Illustration 1: Even if I sensibly represent the parts of the disk defined by the circle in some sense, my representations of these parts are not conscious as long as I cannot distinguish them by drawing a line that divides the disk into two halves, for example. If the property of being conscious is understood in this way, it is clear that the sensible representation of an empty visual field would not be conscious in the relevant sense, because its content cannot be distinguished from anything else by means of our intuition. However, as soon as we start to draw a line within space in our pure imagination, then it is not only this line that becomes an object of consciousness but also the space into which we draw it. The line becomes an object of conscious intuition because we distinguish it from the space into which we draw it. And, at the same time, this space becomes an object of consciousness because we distinguish it from an object within it. Moreover, since there is no phenomenal horizon that is not the phenomenal horizon of something that appears in it, it is only through this distinction from something within it that space can be become an object of our intuitive awareness.⁴⁰

I think that Kant’s arguments for taking synthesis to be an ingredient of the intuition of space have a lot of philosophical appeal.⁴¹ They are directed against the view that we represent infinite space in intuition solely by means of a certain intrinsic phenomenal character. This view is implausible because it seems unclear what infinite space by itself looks like. Kant, in contrast, is not committed to give an answer to this question. For example, he is not committed to taking the phenomenology of the pure intuition of infinite space to be that of the intuition of an empty visual field or to assuming that we are able to intuit infinitely long lines. According to him, the infinity of the phenomenal horizon is noticed by drawing finitely long lines farther and by being aware that no matter how far we extend them, they will always divide, or limit, a still larger space, which surrounds the constructed space. The idea that we could intuit infinite space independently of any such act of sensibly distinguishing it from something within it seems like the idea that we could intuit ‘the night in which all cows are black’, to use the phrase by which G. W. F. Hegel famously made fun of J. G. Fichte’s and F. W. J. von Schelling’s ideas of an immediate relation to the absolute.⁴²

Speaking of Hegel, it is instructive to compare the function that the act of decomposition plays for the intuition of infinite space with that of the act of negation for the representation of the infinite by the conceptual means of the understanding. It seems relatively easy to see how finite beings can have a conceptual representation of the infinite. They start with the concept of the finite as something that has limits in a certain dimension and then, through combining it with the concept of negation, acquire the concept of the infinite as something that has no limits in this dimension. The prima facie problem with an intuition of the infinite seems to be that here no analogous procedure seems to be available that bridges the gap from the finite to the infinite. However, decomposing synthesis is just such a procedure. Like conceptual negation, it allows us to become aware of the infinite through its difference from the finite, which is not totally distinct from it but rather a part within it. Yet decomposition is different from negation as a procedure of the understanding in that it does not start from an independent grasp of the finite. As we have seen, in the decomposition of infinite space, the whole is prior to its parts, and there is no grasping of the finite parts which is not at the same time a grasping of the infinite whole of which they are parts. I think it was this feature of Kant’s theory that Hegel had in mind when he praised Kant’s remarks about the role of the imagination for our intuition of space at the end of the B-Deduction. ‘The productive imagination is a truly speculative Idea,’ Hegel writes in Glauben und Wissen, because it creates a synthetic unity that ‘is not an aggregate of manifolds which are first picked up, and then the synthesis supervenes upon them afterwards’⁴³ but ‘must be conceived, not as produced out of opposites, but as a truly necessary, absolute, original identity of opposites’.⁴⁴

5. Conceptualism or non-conceptualism?⁴⁵

The affinity between Kant and Hegel gives rise to the question of how the proposed interpretation relates to non-conceptualist interpretations of Kant’s account of the intuition of space.⁴⁶ By introducing the idea of a decomposing synthesis, it certainly undermines one important motivation for such interpretations, namely the argument that synthesis could not be a precondition for the intuition of something that is infinite and has a whole-prior-to-its-parts structure. Moreover, the remarks about Kant’s views about the connection between consciousness and discrimination at the end of the last section are directed against a form of non-conceptualism that assumes that space could be consciously grasped in intuition as a ‘brute given’ prior to any synthesis.

However, the present interpretation is also sympathetic to nonconceptualism in several respects. First, although it assumes that synthesis is required for intuition, this synthesis is not conceived of as a conceptual activity. Though it is an activity of the spontaneity of the understanding, this spontaneity works ‘under the name of the imagination’ (B162fn.; B153) and does not bring about conceptual but sensible content. Second, the interpretation only assumes that synthesis is required for making the spatial manifold conscious, not that it brings about this spatial manifold. The spatial manifold itself is given by space understood as the form of outer intuition and hence by the form of a faculty that Kant thinks is fundamentally different from, and irreducible to, the understanding.⁴⁷ Third, the interpretation is in principle even compatible with a form of non-conceptualism that agrees that synthesis is required for space to become an object of conscious intuition but assumes that, prior to any synthesis, space can nevertheless be an object (and not only a form) of intuition, if this intuition is understood as an unconscious representation.

I have to confess, though, that I do not find this last form of nonconceptualism very appealing. On the one hand, it somehow blurs the clear distinction that Kant draws in B160 between space as a form of intuition, which can exist without synthesis, and space as an object of intuition, which requires synthesis, by introducing an intermediate third level at which space is an object of unconscious intuition, which does not require synthesis. I do not think that assuming this third level is really justified by the text.⁴⁸ I am also skeptical that it fits well with Kant’s account of intuition. It is true that Kant allows for unconscious, or ‘dark’, intuition, e.g. of the stars that are indistinctly represented in our intuition of the Milky Way.⁴⁹ Here, the givenness of the objects in intuition does not amount to the phenomenal presence of these objects in consciousness but is rather constituted by causal affection: The stars of the Milky Way are unconsciously intuited partly because they are the objects that affect us in such a way that a blurry intuition of the Milky Way arises. Now, the non-conceptualist cannot transfer this model of givenness to the case of the unconscious pure intuition of space and assume that space is unconsciously intuited because it affects us. The reason is that, as a form of sensibility, space is causally inert and cannot affect us in the way the stars can.⁵⁰ As Kant argues at length in § 24 of the B-Deduction, the affection involved in pure intuition is rather one that is done by the spontaneous understanding. It results precisely in the activity of imaginative sensible synthesis that makes intuition conscious. This still allows for cases of unconscious pure intuition. However, such cases are not ones where we have pure intuition prior to any synthesis, as the non-conceptualist in question wants to assume, but rather ones where the synthesis does not suffice to make an intuition entirely conscious. This is precisely the case in the above example of the unconscious representation of the possible parts of an (consciously intuited) circle before its actual division.⁵¹ So, I find it much more plausible to assume that, although space as a form is an irreducibly non-conceptual element of pure intuition, this element has to be combined with a second causal factor, namely the activity of the understanding, in order to become an object of an either conscious or unconscious intuition.⁵² At least I do so until the non-conceptualist comes up with an alternative model for unconscious pure intuition.

Beside the question of whether synthesis is required for a conscious representation of space, the debate about Kantian non-conceptualism is also concerned with the question of whether certain essential features of space, most notably its unity, are brought about by this synthesis or are rather independent of it. The present proposal implies that synthesis brings about the intentional unity of space, i.e. the unity that space has as an object of conscious intuition. We have to be careful, though, not to confuse the claim that synthesis brings about a certain feature with the claim that it brings about this feature all by itself. X can bring about Y even if there are other causal factors besides X without which Y would not exist. So, the claim that synthesis brings about the intentional unity of space is compatible with assuming that there are other factors — e.g. structural features of space as a form of intuition — without which space would not be a unified singular whole.⁵³ In fact, I think it is pretty obvious that the unity of space cannot exclusively originate from the act of synthesis performed by the understanding. I agree with the non-conceptualists here that we should take seriously Kant’s insistence that the faculty of sensibility cannot be reduced to that of the understanding and that the singularity of space is essentially connected to the fact that space is an object of intuition understood as a means of singular representation. Hence, it is much more plausible to assume that the intentional unity that space has as an object of conscious intuition is also partly grounded in the specific nature of space as a form of intuition.⁵⁴

This last remark is compatible with both a mild and a more robust form of non-conceptualism about the unity of space. According to the mild form, synthesis is a genuine second causal factor in bringing about the unity of space. According to the more robust form, space has its unity already as a form of intuition, and synthesis is only required to make this unity conscious, i.e. turn it into an intentional unity. Although my general account could be embraced by proponents of both forms of non-conceptualism, I am in fact more sympathetic with the first variant. I think the more robust variant loses its attraction once we make more explicit what it would mean for a mere form of intuition to have unity. In general, the unity of space consists in its being a single all-encompassing whole that precedes all of its parts (A25/B39). That space has this feature already as a form of intuition would mean that, for all cases where someone intuits something at some time according to this form, there are matters of fact to the effect that the intuited objects all belong to one and the same space. For example, when subject 1 constructs one triangle in pure intuition and subject 2 another or when subject 1 constructs one triangle now and another one later on, then there would be facts of the matter as to whether the triangles belong to one and the same space and hence all the constructed triangles would stand in spatial relations towards one another. I do not think that Kant thought of forms of intuition in this way. It seems to me that the question of whether there is just one or rather many spaces only has a determinate answer once we consider space not as a mere form, but as an object of intuition, which, according to my interpretation, requires synthesis as a second causal factor. Moreover, I think that Kant’s argument in the Transcendental Analytic presupposes that facts about transtemporal and intersubjective spatial relations are not already constituted by sensibility and its form alone. However, this obviously raises a whole variety of controversial questions, which I cannot further discuss here. So, in the following, I will confine myself to the claim that the intentional unity of space, i.e. the unity that space has as an object of conscious intuition, requires synthesis but is not fully constituted by it. In the next section, I will show how composing and decomposing syntheses can contribute to this kind of intentional unity.

6. Synthesis and the unity of space

As I have explained in Section 1, there are two kinds of intentional unity that the objects of outer intuition can have. There is the unity of particular spatial objects and regions, and there is the unity that space itself has by being one single all-encompassing whole that precedes all of its parts. I will explain in the following how both kinds of unity are brought about by an activity of the imagination, the former by composing synthesis, the latter by decomposing synthesis.

In general it is not difficult to see how decomposition can create intentional unity once we have understood how it can bring about an awareness of a manifold of parts as such. An awareness of a manifold of parts as such is ipso facto an awareness of those parts as parts of a common whole. Consequently, decomposing synthesis always brings about an awareness of the whole which those parts jointly constitute. In doing so, decomposing synthesis also brings about the intentional unity that this whole has with respect to its parts. This can happen in cases where the whole is already given to us, e.g. the case of dividing the disk by drawing a line. In such cases, decomposition of the whole merely brings about an awareness of the unity that the whole has in virtue of having the specific parts it does. But there can also be cases where the whole is only given to us through the act of decomposition, e.g. the case of decomposing infinite space by constructing a determinate spatial object within it, which brings about an awareness of space as one whole that has this object and its horizon as parts. Now, the unity of space does not only consist in its being a whole that encompasses one particular geometrical object as a part, but it is a unity that space has by being a single all-encompassing whole (A25/B39), i.e. a whole of which all determinate spaces whatsoever are parts. Can the unity of space as something that encompasses a multitude of things in it also be given through decomposition?

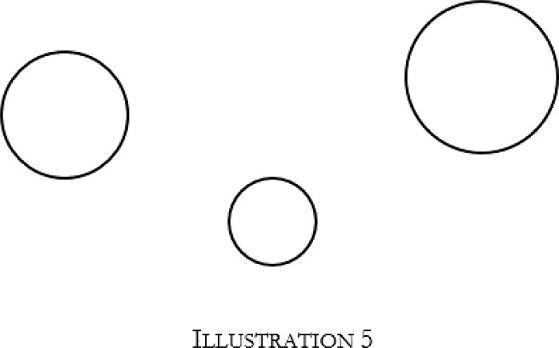
In order to see that it can, we should have a look at one further illustration, which shows what we represent in our intuition when we construct a multitude of geometrical objects, for example three circles a, b, and c.

There are two different kinds of unity involved in what is presented here. First, there are cases of unity brought about by compositional synthesis: the unity that each one of the three circles a, b, and c has by comprising a multitude of line-segments arranged in a certain way, and the unity among a, b, and c which they have once we ‘run through’ them one after the other and ‘take them up’ into our consciousness, e.g. by seeing them as a plurality of three circles. Second, there is also a unity that a, b, and c have by all belonging to one common whole, namely the space that encompasses all of them and that establishes a unity not only among a, b, and c but also among these three objects and all other possible objects that could have a certain position in space. This unity is not brought about by a compositional synthesis, but results from the fact that when we construct the three circles, it is not the case that each one of them comes with its own phenomenal horizon. Rather, the act of decomposition that we have to perform in order to bring them to our awareness results in an awareness of three distinct determinate objects and one common horizon that they all share. Thus, this act presents to us a whole that consists of this horizon and the three circles as parts and hence encompasses and gives unity to the latter. It presents to us space as a whole that embraces a multitude of objects.

Now, representing space as encompassing a, b, and c still is not representing it as all-encompassing. But this need not worry us. The task of decomposing synthesis is to present infinite space, which in fact has an all-encompassing unity, in intuition, not to present it as having this unity. Just as we had to distinguish between the claim that we have an immediate intuition of infinite space and the claim that we have an immediate intuition of its infinity, we should not confuse the claim that we have an intuition of all-encompassing space with the claim that we intuit its ‘all-encompassing-ness’. However, just as there was a mediated route from our intuition of space to an insight in its infinity, there is an insight in the unity of space that is grounded in intuitions like that displayed in Illustration 5. In the case of the infinity of space, we learned, through free imaginative variation of the intuition of the lines in Illustration 4, that no matter how far we extended the two drawn lines, the space into which we have drawn the lines would always be larger than the one we had carved out from it through decomposition. Similarly, we can start from Illustration 5 and let our imagination add further geometrical objects in addition to the three circles presented there. We will soon see that no matter how many further objects we should add to these three circles, these objects would all be placed in the same singular space that is already intuitively present in Illustration 5. Thus, this space is a mereological whole that is prior to all of the parts that result from its decomposition and hence has a unity that precedes all those unities that are brought about by acts of composition.

It is important to note that the unities brought about by acts of compositional synthesis (the unity of determinate objects or determinate pluralities of objects) and the unity brought about by acts of decomposing synthesis (the unity of all-encompassing space) are mutually dependent on each other. We cannot grasp the unity of a determinate intuited spatial object, or group of such objects, without intuiting this object as being in space, and we cannot grasp the unity of space as an object of intuition without intuiting space as something in which determinate spatial objects appear. In fact, the two types of acts of synthesis that bring about these unities are just two aspects of the same token acts of the imagination. Drawing one or more lines in order to construct a geometrical object by compositional synthesis just is a case of decomposition of the space in which we draw them, and any act of decomposing space always is an act of composing one or more lines.

I think that recognizing the distinction and mutual dependence of two kinds of unities brought about by the synthesis of the imagination is important for the task that Kant has set himself for the second part of the B-Deduction, namely to explain how it is possible that the categories are applicable to all objects of experience (B159–60). Kant thinks that this explanation can be provided if we manage to prove that the unity that we think through the categories is already contained in the sensible manifold to which we apply them. His general strategy for showing this is to argue (i) that any sensible manifold is given in a priori forms, (ii) that the unity we think through the categories is no other than the one that these forms display once they are themselves objects of a priori intuitions (B144–5 and § 26), and (iii) that this in turn is the case if these a priori intuitions are brought about by a synthesis of the imagination that is somehow an effect of the same synthetic function of the understanding that we find displayed in the application of the categories in judgements (B161f.; A79/B104f.).

Now, no matter how we understand the details of these three controversial steps, we should note that there are in fact two kinds of unity that we presume to hold when we apply the categories in judgements to objects of experience. First, there is the unity that holds between the parts and features of determinate particular objects or of determinate pluralities of such objects. Let us call this kind of unity determinate unity. We can illustrate this kind of unity by means of Illustration 5 above, if we now take it to represent three material bodies A, B, and C. We presume that each of these bodies has determinate unity when we describe its properties as the accidents of one common substance, and we further presume a determinate unity among A, B, and C when we describe these three objects as standing in causal relations, as having specific distances from one another and as having sizes and masses that stand in determinate quantitative relations to one another. Second, by applying the categories to objects of experience, we also presume another kind of unity, one that does not hold among the members of determinate pluralities of objects or their features and parts, but rather among any given determinate object, or determinate plurality of objects, on the one hand, and the indeterminate plurality of all other possible objects that could ever become objects of our experience, on the other. We can call this unity the unity that objects have by being part of one world, or simply world-unity.⁵⁵

That the presumption of world-unity is indeed an ingredient of the application of the categories can most easily be seen in the case of the category of causality. When we say that substance A causes substance B to be in a certain state, we claim that there is a law that governs the succession of their states.⁵⁶ But a law is a rule that applies not only to A and B but also to all other possible objects of experience in similar states. In general, two objects cannot stand in a causal relation to each other without standing in some relation of unity with all other possible objects of experience. The same holds for the other categories. If we say that substance A has a determinate size and mass, that means not only that it is determined how these quantities relate to the size and mass of B and C but also that there are objective facts about how they would relate to those of any other possible object of experience. Other such examples abound. So, we should agree that by applying the categories to objects of experience, we presume that they participate in some determinate unity as well as in a world-unity and that we presume the latter unity by presuming the former.

As a consequence, in order for Kant’s project in the second part of the B-Deduction to be successful, he has to show that the presumption of both of these kinds of unities is justified. That means, he has to show that they can both be found in the spatio-temporal manifold to which we apply the categories, because they are both brought about by a spontaneous synthesis of the imagination that is an essential ingredient of our pure intuition of space. But this is exactly what Kant can assume if the proposed interpretation is correct and one and the same token act of figurative synthesis can bring about two kinds of unities in a priori spatial intuitions. If we take the example of drawing the three circles a, b, and c, this act of the productive imagination is a case of compositional synthesis that brings about the unity of a determinate intuition (the intuition of the three circles as standing in certain relations to one another), but it is also a case of decomposing synthesis because it decomposes space into the three areas that are enclosed by the circles and their common horizon. This decomposition establishes a unity between them and all other possible spatial objects that could appear in this same horizon. This latter unity guarantees that all the different determinate spatial regions that could ever be objects of our determinate intuitions belong to one single whole and hence that all the empirical objects that could ever appear within it make up one common world.

7. Conclusion

I have argued that Kant’s claim that spatial intuition presupposes a synthesis of the imagination has a more complex meaning than is usually assumed. On the one hand, it means that any kind of intuition of a determinate spatial object or plurality of such objects presupposes an act of compositional synthesis. On the other hand, it means that the whole of space is only given to us in intuition by an act of decomposing synthesis through which we distinguish determinate spatial objects from their phenomenal horizon. Acknowledging that there is the second kind of synthesis allows us to solve the puzzle of how synthesis can be presupposed by the intuition of something that is infinite and prior to its parts. We have also seen that the two activities of synthesis are mutually dependent on each other: Just as there cannot be an intuition of a determinate spatial object that does not present this object as being in space, there can be no intuition of space unless it presents space as something in which a determinate spatial object appears. Finally, I have argued that the two kinds of synthesis bring about two different kinds of unity within the sensible manifold: the unity that the different parts of spatial pluralities have by all being compositionally synthesized into a determinate whole and the unity that space itself has by being a whole that encompasses all determinate spatial objects that could ever be carved out from it through decomposition.⁵⁷