1. The Question
Pencils ready! For each pair, circle the city that you think has a larger population (in the city proper), and then rate how confident you are on a 50–100% scale:
-
1)
Denver or Phoenix? Confidence: _____%
-
2)
San Jose or Seattle? Confidence: _____%
-
3)
Indianapolis or Columbus? Confidence: _____%
That rather striking result—the so-called ‘overconfidence effect’—is common: on a variety of tests, people’s average confidence in their answers exceeds the proportion that are right (e.g. Lichtenstein et al. 1982; Glaser and Weber 2010). Many have inferred that such people tend to be overconfident: more confident than it’s rational for them to be, given their evidence.2 Many have used these (and related) results to paint unflattering pictures of the human mind as prone to irrationality and bias.3 And many others have invoked overconfidence in particular to explain a variety of societal ills—from market crashes, to polarization, to wars.4 Daniel Kahneman summed it up bluntly: ‘What would I eliminate if I had a magic wand? Overconfidence’.5
Fair. But how exactly did we conclude that people are overconfident? The most common type of evidence—the type I’ll focus on until §6—is binary-question (‘2-alternative-forced-choice’) calibration studies like the one you just took. Ask people questions with two possible answers; have them guess and report their confidence (degree of belief or credence) in each guess; then group guesses by confidence-level and plot the proportion of guesses that are right at each level. This generates a calibration curve—see the right side of Figure 1 on page 3. Say that a person is calibrated (at x%) if x% of the claims that they’re x% confident in are true. They are over-calibrated (at x%)—in the sense that their confidence needs to be lower in order to be calibrated—if fewer than x% of such claims are true. And they are under-calibrated (at x%) if more than x% of such claims are true.
That’s the evidence: people are (often) over-calibrated. This is an empirical observation about the relationship between actual confidence and proportion true. How does it support the normative conclusion about the relationship between actual confidence and rational confidence—namely, that people are (often) overconfident? Well, if you’re x% confident in a bunch of (independent) claims, then probabilistic coherence requires you to be confident that roughly x% of them are true (see §2). And it’s natural to think that if your confidence is rationally placed, you’ll be right: rational people know their limits, and so know how often their opinions tend to be right. (Right?) If so, then observing that people don’t know their limits seems to suggest that they’re too confident—overconfident.
Though natural, this is a substantive inference: it moves from an empirical observation (‘you are miscalibrated—i.e. wrong about how often your opinions at various levels of confidence are right’) to a normative conclusion (‘you are irrational’). Call it the right-and-rational inference since it presupposes that we can expect that rationality will stand or fall with being right about how often your opinions are correct.
The Questions: What is the connection between being rational and being right? More specifically: When is the right-and-rational inference warranted? When is it not? And what does that tell us about how to interpret calibration studies?
The Plan: I’ll first say what sort of connection the right-and-rational inference assumes, explaining why the extant literature has failed to articulate it (§2). I’ll then use the notion of deference to show why we should expect such a connection generically (§3). However, it turns out this connection will break in predictable ways: often miscalibration is evidence for rationality (§4). I’ll argue that this provides both a foundation for and a refinement to the standard methodology: in testing whether people are rational, the null hypothesis should not be that they’ll be calibrated; rather, we must first predict the rational deviations from calibration, and then compare people’s performance to those predictions. I’ll show how in principle this can be done, and that doing so complicates our interpretation of calibration studies (§§5–6). I’ll make this argument specifically for binary-question tests, but §6 will suggest that the arguments carry over to other formats—such as placement (Kruger and Dunning 1999) and interval-estimation (Moore et al. 2015b) tests. In short: although calibration scores are a great guide to how wrong your past judgments were—and therefore, how to do better in the future (Tetlock and Gardner 2016)—they are a flawed guide to how rational those judgments were.
The Upshot: If this is correct, it shows that certain philosophical and psychological debates are more entwined than has been realized. Philosophical debates about deference principles can inform the methodology of calibration studies. Meanwhile, the methods of such studies suggest that—although there’s arguably no necessary connection between being rational and being right6—how often people are right is often good evidence about whether they’re rational (and vice versa). Thus this paper supports the growing interest in connecting philosophical accounts of rationality with psychological investigations of it.7
2. The Problem
Calvin walks in. We want to know if he’s (on average) overconfident in a certain set of opinions. What do we do?
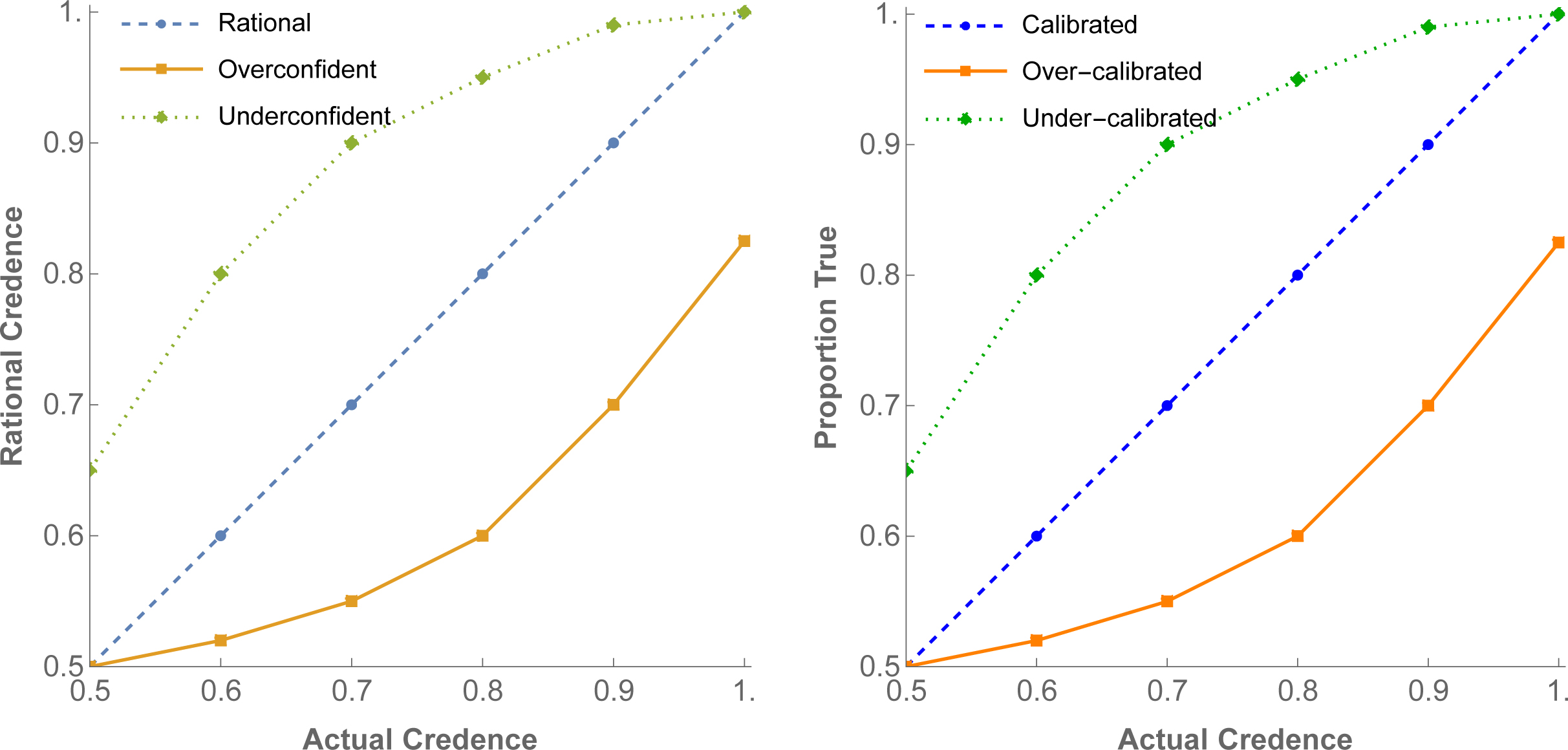
First question: what do we mean? I’ll follow the literature and say that he’s ‘overconfident’ in a given claim if his credence is more extreme—closer to 0 or 1—than it’s rational for him to be, given his evidence. Let’s focus on the claims he’s inclined to guess are true, i.e. is at least 50% confident in.8 Group guesses by their confidence-level on the x-axis, and plot the average credence it’d be rational for him to have in each group on the y-axis—imagining for the moment that we know the latter (Figure 1, left). He’s (on average) rational if, among all the claims he’s x% confident in, he’s (on average) rational to be x% confident in them—the line is diagonal. He’s (on average) overconfident if, among all the claims he’s x% confident in, he’d (on average) be rational to be less than x% confident in them—the curve is bent. Imagine he’s controlling a left-right slider for his credence; he tends to be overconfident if tends to push the slider further right than he should, thereby overshooting the diagonal line (and confusingly, ending up with a calibration curve under the diagonal line); he’s underconfident if the reverse.
Of course, we don’t know how confident he’s (on average—and now I’m going to stop saying ‘on average’ since you know what I mean) rational to be, so we don’t know which curve describes Calvin. How to get evidence about that? We need evidence about the two quantities that determine it: given some set of claims, we need Calvin’s average credences in that set, , and the average credences it’d be rational for him to have, . Let’s use Calvin’s opinions to determine the set of claims—say, the set of claims on our test that he is 80% confident in; call those his 80%-opinions. (Repeat the reasoning with his 70%-opinions, etc.) Then ; Calvin is overconfident on that set if , and underconfident if . What we need is evidence about : the average credence Calvin would be rational to have in these claims.
This is important. To ask the question psychologists are asking—‘Is Calvin overconfident?’—is to presuppose that these quantities and exist. It’s fairly uncontroversial that the former does, but some will be surprised by the latter—that there’s a number that potentially-differs from Calvin’s actual credences and captures the average credence he should have, given his evidence.
Three points. First, it shouldn’t be that surprising. After all, sometimes some people are being overconfident, and surely we can gloss this as ‘being more confident than they should be’. That entails that there are facts about how confident they should be—i.e. facts about . Second, presupposing that exists doesn’t say anything about how it’s determined. Nothing says it needs to be ‘objective’; even subjective Bayesians—who think you can choose any prior, but that once you do you’re rational only if you update it properly—should agree that exists. Third, for simplicity I’ll model and as precise numbers, rather than more complicated objects, like (vague) sets; most of the lessons will carry over.
So let’s suppose that exists. I’ll go slightly further and make the simplifying assumption that there’s a function such that, given any of Calvin’s 80%-opinions (guesses) gi, outputs a number expressing how confident he’d be rational to be in gi. (If , he’s rational to be 80% confident; if , he’s overconfident.) The average is then 9.
Even if exists, we don’t know what it is—among many reasons, we don’t know what Calvin’s evidence is! Thus once we know what Calvin’s genuine 80%-opinions are (let’s trust the psychometricians have figured that out—see O’Hagan et al. 2006; Moore 2007; Moore and Healy 2008), we must somehow get evidence about what those opinions should be, i.e. what is. How can we get evidence about this normative quantity?
I know of no study that addresses this question explicitly. In practice, they proceed by measuring another empirical quantity: the proportion of Calvin’s (say, 80%-)opinions that are true; call this . Combined with , this will tell us whether Calvin is calibrated; if , then he’s (approximately) calibrated; if , he’s over-calibrated; if , he’s under-calibrated (Figure 1, right, focusing on x-axis value of 0.8). Researchers assume that so long as the experiment is properly done, then observing that Calvin is over-calibrated provides evidence that he’s overconfident .
Once stated this way, it’s clear that this methodology is warranted when and only when proportion-true can be expected to be a good indicator of average-rational-credence —only when we should expect the two y-axes in Figure 1 to align.
This is a problem. Although the right-and-rational inference is about the relationship between rational opinions and actual opinions , I know of no study that explicitly represents the former as a variable to be investigated. None of the studies cited in this paper do so.10 (Perhaps, I speculate, because empirical psychology discourages explicit modeling of normative quantities.) Thus none state the assumptions needed establish that we can expect to be a good indicator of in the case at hand.11 Yet the empirical observation that people are over-calibrated is evidence that people are overconfident only when we have reason to expect this.12
Bayesianism to the rescue? It’s well-known that Bayesians must expect themselves to be calibrated on any given set of claims. Take such a set G. Calvin is calibrated on G iff, of all the claims in G he’s x% confident in, x% are true. Focus on the claims he’s (say) 80% confident in, g1, …, gn. To be coherent, his best estimate for the proportion of the gi that are true must be 80%—if it wasn’t, he’d revise his opinions in the gi. Moreover, so long as he treats the claims (roughly) independently, then as the number of gi grows, he must be increasingly confident that close to 80% of them will be true.13 Thus if Calvin is (Bayes-)rational, he’ll be confident he’s calibrated on the test.
But in order for his (mis)calibration to provide us with evidence about his rationality, the relevant question is whether we should be confident that if he’s rational, he’ll be calibrated. Since we are not him, there’s no theorem that we should expect this. Often we shouldn’t. Of course, sometimes we should—sometimes provides evidence about . But just as clearly, sometimes it won’t. As the philosophical literature emphasizes (footnote 6), there is no necessary connection between being rational and being right at any level of statistical generality.
Case 1: Rajat uses all his evidence rationally. He’s sure that he has hands, confident he’s healthy, and suspects he’ll soon grab lunch. But though rational, Rajat is wrong on all these fronts—unbeknownst to him, he’s a (rational) brain-in-a-vat. Rajat is over-calibrated, yet this doesn’t suggest he’s irrational.
Mundane cases make the same point. Case 2: Georgie is quite wrong in most of her geographical opinions. Is that evidence that she’s over-confident? Not if we know that her geography teacher gave her an outdated textbook—she’s misinformed, not irrational.
Likewisqe, there are cases where someone has high-quality evidence, and yet the right-and-rational inference fails. Case 3: I have a coin in my pocket that’s 60% biased toward heads; I’m about to toss it 100 times. How confident are you, of each toss, that it’ll land heads on that toss? Write that number down—I’ll look at it in a second. First to toss the coin (…done). It landed heads only 30 times . Looking at what you wrote, it turns out you were 60% confident that each toss would land heads. Only 30% did—you’re over-calibrated . Is this evidence that you were overconfident (that )? No; it’s just evidence that you were unlucky.
Similarly, sometimes we can know beforehand that your rational opinions will be miscalibrated. Case 4: I have an urn of mis-printed coins—60 of them are double-headed; the remaining 40 are double-tailed. I’m about to pull a single coin from the urn and toss it 10 times. How confident are you, of each toss, that the coin I draw will land heads on that toss? 60%—and rationally so. Yet you know that I’ll draw either a double-headed or a double-tailed coin. If the former, all the tosses will land heads—100% of the things that you’re 60% confident in will be true . And if the latter, then none of them will land heads—0% of the things that you’re 60% confident in will be true . Either way, you’ll be rational to be miscalibrated.
Finally: we can almost always expect that certain classes of rational opinions will be miscalibrated. Case 5: Suppose you’re about to take a representative test from a set of questions on which your guesses tend to be accurate and your opinions are always rational. Still, your guesses aren’t perfect—sometimes you’ll be wrong. Consider the set of guesses you’ll be wrong about, and the set you’ll be right about. You won’t know what they are until the answers are revealed, but you know you’ll be miscalibrated on them—0% of the claims in will be true, but your average confidence in them will be higher than that; and 100% of the claims in will be true, but you average confidence in them will be lower than that. More generally, we should always expect that people will be over-calibrated on sets like ‘the answers they tended to get wrong’ and under-calibrated on sets like ‘the answers they tended to get right’.
Upshot: it’s easy to imagine scenarios in which rational people are systematically miscalibrated. Obviously such scenarios are contrived, so it may often make sense to discount them. Surely, in some sense, we should expect that rational opinions will tend to be right—that’s the point of being rational, after all! The question is: When, why, and in what sense should we expect this?
My goal is to answer this question. I’ll articulate a probabilistic connection between being rational and being right that explains why the right-and-rational inference works in simple cases (§3), but also reveals that it will fail in systematic ways (§4). §5 will use this fact to propose a refinement of the methodology of calibration studies.
But before moving on, I should say how this project relates to theoretical points made in the calibration literature.14 Ecological approaches suggest we must control for potentially-misleading information by choosing representative questions from a natural domain (Gigerenzer 1991; Gigerenzer et al. 1991; Juslin 1994; Juslin et al. 2000; Hoffrage 2004). Error-model approaches argue that regardless of how questions are selected, there will be stochastic errors (‘noise’) in both the selection of items and in subjects’ reporting of their credences that can lead to them being locally miscalibrated even if their true opinions are calibrated overall (Erev et al. 1994; Pfeifer 1994; Juslin et al. 1997, 1999, 2000). Similar points have been made using information asymmetries among subjects (Moore and Healy 2008; Jansen et al. 2018). In response, researchers have built models of how people could arrive at their credences in rational ways, and yet nonetheless we might expect them to be miscalibrated (cf. Benoît and Dubra 2011).
I agree, but the point is broader. These researchers have proposed particular, rational-seeming mechanisms,15 and shown how they lead to miscalibration. I’m going to show that no matter the mechanism, rational opinions should be expected to be miscalibrated in systematic ways. Establishing this becomes possible once we represent the rational opinions as variables to be investigated. Interestingly, these rational deviations from calibration turn out to be broadly consistent with some of the main empirical trends (§5). But more importantly, they show that we’ve been using the wrong yardstick. In assessing whether people are overconfident, we should never simply compare their calibration curves to the diagonal calibrated line—rather, we must compare them to the predicted rational deviations from this calibrated line. I’ll show how we can predict these rational deviations based purely on to what extent we should defer to what’s rational for our subjects, without making any assumptions about mechanism.
3. The Insight
When are we warranted in performing the right-and-rational inference?
Start by making things simple. A single subject—Calvin—was given a calibration test; the questions were selected at random from a geography textbook. He knows everything you do about the setup. Consider all the guesses that he was 80% confident in—his 80%-opinions. All you’re told is what proportion of them were true. I claim that in this simple scenario, the right-and-rational inference is warranted: rational people can be expected to be right about their accuracy. Thus if you learn that (roughly) 80% of Calvin’s 80%-opinions were right, you get evidence that those opinions were rational; if you learn that far fewer (or far more) than 80% of these opinions were right you get evidence that he was overconfident (or underconfident). That is: even without a necessary connection between being rational and being right, there is often a robust evidential connection between them. This is the insight behind calibration studies.
Why is it correct—and when can it fail? Here’s the basic idea of this paper. Calvin has more information about his 80%-opinions than you do. Thus absent any defeaters you should defer to the opinions it’s rational for him to have, R. As we saw in §2, those (Bayes-)rational opinions will expect themselves to be calibrated, i.e. they’ll expect that the proportion-true () will be close to the average-rational-credence (). (And hence expect that if Calvin’s actual opinions deviate from , they’ll be miscalibrated.) Absent defeaters, we should defer to these rational expectations; thus we should expect the same thing: conditional on Calvin being rational (), we should expect him to be calibrated; conditional on him being overconfident (), we should expect him to be over-calibrated. Turning this around (via Bayes theorem): learning he’s over-calibrated provides evidence that he’s overconfident. Absent any defeaters, the right-and-rational inference is warranted.
But things change if we do have defeaters. If we know something Calvin doesn’t, we should no longer defer to the opinions that are rational for him to have; as a result, we shouldn’t necessarily expect rationality and calibration to pattern together. For example, if we know the test is ‘tricky’ for him, then we should expect that if he’s rational, he’ll be over-calibrated—hence over-calibration will be evidence for rationality.
This section explains how this reasoning works when you don’t have any defeaters; §4 explains why it fails when you do.
Begin with a parable. Long ago, Magic Mary possessed a variety of magic coins—some were biased to come up heads almost every time; others to come up heads 90% of the time; others 80%, and so on. The coins had special markings on them—on some, Washington has a large nose and small ears; on others, he has a thin neck and bushy eyebrows; etc. If you knew how to decipher the markings, you could infer the bias of the coin.
Mary tossed the coins many, many times. She kept fastidious records: for each toss she drew a picture of the coin’s markings on one side of a stone tablet, and the outcome of the toss (heads or tails) on the other. Alas, Magic Mary and her magic coins are long gone—but many of the tablets remain, stored in various historical archives. And alas, no one can decipher the markings to determine the coins’ biases.
… or so we thought! But now bias-busting Bianca claims that she can decipher the markings and determine the coins’ biases. How can we test her claim, given that we don’t know how to decipher them?
Here’s a good strategy. Go to an archive that contains a representative sample of tablets; draw a tablet at random; show her the markings-side and have her announce her guess as to whether it landed heads or tails along with her confidence in that guess; write down whether she got it right (but don’t tell her); then draw a new tablet and repeat. Suppose we do this with many tablets, and then notice that of the guesses she was 80% confident in, 79% were correct. That should boost our credence that Bianca can decipher the coins. Conversely, if we learn that only 60% of those guesses were true, that should lower our credence that she can decipher the coins. That is, whether Bianca is right as often as she expects (whether she’s calibrated) provides evidence about whether she can decipher the coins.
Why? Before I tell you about Bianca’s calibration, you should think to yourself:
Thus if you learn that she’s calibrated, you learn something that’s much more likely if she can decipher the coins than if she can’t—which means, by Bayes theorem, you get evidence that she can. Conversely, learning that she’s over-calibrated provides reason to think she can’t decipher the coins.If she can reliably recognize the coins, then the coins she says ‘80%’ on will be 80%-biased in the way she predicts—meaning (I expect) that around 80% will land as she predicts. Meanwhile, if she can’t decipher the coins, it’s much more likely that a different proportion will land the way she predicts.
Thus the driving force of the inference is that hypotheses about whether she is deciphering the coins’ biases, over-estimating them, or under-estimating them, each have direct implications for how many of the coins you should expect to land the way she guesses. This is because of the Principal Principle (Lewis 1980, 1994; Hall 1994; Briggs 2009b): you should defer to the biases of the coins in setting your (conditional) opinions in how the’ll land, and this deference to each coins’ bias is independent of the others. More precisely: deference says that conditional on the coins having an (average) bias of x% toward Bianca’s prediction, you should be x% confident in each of those predictions; independence says that this x% confidence remains even if you were to learn how the others coins landed. Combined, these constraints entail that conditional on the coins having an average bias of x% toward Bianca’s predictions, you’re confident that roughly x% of them will be true.
Upshot: for the right-and-rational inference to work in Calvin’s case, analogous deference and independence principles must hold. What does the analogy amount to? For each tablet Bianca was shown, there was a fact about what the corresponding coin’s bias was. Likewise: for each question Calvin assesses, there is a fact about the rational degree of confidence he should have in his answer (R(gi)). We wanted to know whether Bianca could reliably line up her credences with the coins’ biases. Likewise: we want to know whether Calvin can reliably line up his credences with the rational credence. In Bianca’s case, the inference went through because we should defer to the biases of the coins, and do so independently of how her other predictions turn out. Thus in Calvin’s case the right-and-rational inference will go through when and because we should defer to the rational credences for Calvin to have in his answers, and do so independently of how his other guesses turn out.
Now more precisely. As we’re focusing on binary-question tests, I’ll assume that when presented with a pair of possible answers, {p, p′}, Calvin becomes sure that one of them is correct and adjusts his credences accordingly, guesses the one that he thinks is more likely to be true (picking randomly if he’s 50-50), and reports his credence that it’s right. (For questions with more than two answers, complications arise—see §6.2.)
Consider all of the guesses Calvin assigns 80% credence to—his 80%-opinions. Label them g1, …gn, so gi is the claim that Calvin’s ith (80% confident) guess was right. (Suppose we know that there are n such opinions—the reasoning generalizes if we’re unsure.) We can entertain different hypotheses about the rational opinions for Calvin to have. As discussed in §2, I’ll assume that R exists and is probabilistic, but I make no assumption about how it’s determined. Let be the average rational opinion for Calvin to have in the gi, i.e. the average confidence he should have in the claims he’s in fact 80% confident in. We are, again, uncertain what R (and hence ) is—it is what we must get evidence about in order to get evidence about whether Calvin is overconfident.
Assume for now that we don’t know which geographical claims he was 80% confident in, so we have little evidence about whether each gi is true—the only things we know about gi is that it was on the test and Calvin was 80% confident in it.
What does it mean for you to defer to the rational credences for Calvin to have, in a way that makes his case analogous to Bianca’s? Let P be a probability function representing your prior rational credences, before learning about the outcomes of the test.16 In general, Deference is a constraint on conditional opinions: you defer to the weather forecaster even when you don’t know their predictions, because conditional on the forecaster being x% confident of rain, you’re x% confident of rain; P(rain|forecast = x) = x. Likewise, you defer to the bias of one of Bianca’s coins even when you don’t know the bias, because conditional on the coin being x-biased toward heads, your credence in heads is x: P(heads|bias = x) = x. These conditional credences obviously constrain how you’ll update your opinions if you learn that the forecaster is x-confident of rain or the coin is x-biased toward heads—you’ll adopt credence x. Bayes theorem therefore implies that they also constrain how you’ll update in response to other bits of evidence. For example, if you learn that the coin landed heads 90% of the time, that should increase your credence that it was biased toward heads (e.g. that bias = 0.9, since that’s exactly what a 0.9-bias would’ve led you to expect).
Back to Calvin. Deferring to the rational opinions for him to have means:
Remember: since all you know about the gi is that they were guesses Calvin was 80% confident in, you have no distinguishing information between them. Thus Deference holds for any given gi iff it holds for all of them.Deference: Conditional on the average rational credence for Calvin (in his 80%-opinions) being x%, you should be x% confident in each of them.
For all .
When Deference holds, it says explicitly what opinions you should adopt if you learn what the average rational credence () is. But, of course, you’ll never learn that (that’s the whole problem!). Does that mean it’s useless? No. As above (via Bayes theorem), it constrains your responses to other bits of evidence. In particular, since it tells you what proportion of gi to expect to be true if Calvin is rational (namely, 80%) and if he’s overconfident (namely, less than 80%), Deference implies that learning about what proportion of the gi are true provides evidence about .
Deference is an interpersonal, rationalized, and ‘averaged’ generalization of the well-known Reflection Principle (van Fraassen 1984; Briggs 2009a; Christensen 2010b; Mahtani 2017).17 It tells you to defer to the opinions it is rational for Calvin to have, not the opinions he in fact has. In our simple setup you don’t know which claims were his 80%-opinions, so you have little evidence about the gi. Meanwhile, Calvin has strictly more evidence than you about them—he knows all you do about the setup of the test, plus he knows which claims he was 80% confident in, and therefore knows which facts bear on their truth. Since you have no reason to think Calvin’s evidence is misleading (you have no defeaters), it seems reasonable for you to defer to his rational credences.
Of course, whether Deference holds in a given case obviously depends on the details. My aim is not to argue that it does hold in a particular class of cases. Rather, my aim is to establish that Deference is key to understanding when the right-and-rational inference works—and when it fails. Slightly more precisely, I’ll show that Deference explains why you should often initially expect proportion-true () to be a good guide to average-rational-credence (). The right-and-rational inference will in general be warranted when learning about the outcome of the test doesn’t defeat this initial expectation; it’ll be unwarranted when it does (§4).
More generally, how plausible Deference is depends on hard epistemological questions. Whether interpersonal deference principles hold is highly dependent on the debate between uniqueness and permissivism (e.g. White 2005; Schoenfield 2014, 2019; Horowitz 2014b, 2019; Greco and Hedden 2016; Schultheis 2018). Whether rationalized deference principles hold is highly dependent on debates around higher-order evidence (e.g. Williamson 2000, 2019; Christensen 2010b; Lasonen-Aarnio 2013, 2015, 2019; Elga 2013; Horowitz 2014a; Salow 2018; Dorst 2020a,b). Deference will be a theorem in our setup given uniqueness plus higher-order certainty; it’ll be approximately true under some (but not all) weaker theories—see §6.1.
To begin to see the importance of Deference for the right-and-rational inference, notice that its failure explains why the inference is unwarranted in many of our initial cases (§2). You shouldn’t defer to Rajat (Case 1) or Georgie (Case 2), because you know things they don’t—namely, that he’s a brain in a vat, and she has an outdated textbook. Similarly, when I saw that my 60%-biased coin landed heads only 30 times (Case 3), I had evidence that you didn’t when you formed your (rational) opinions about it. Likewise for Case 5—I shouldn’t defer to your opinion about gi if I know that it’s in the set of guesses you were wrong about, since you (of course) didn’t know that.
But Deference doesn’t explain why the right-and-rational inference fails in our case of the misprinted coins (Case 4, page 5). I haven’t yet drawn the coin from the urn, so I don’t know anything that you don’t—yet I know you’ll be miscalibrated.
This is where we need our second assumption: Independence. This says that your opinions about whether Calvin’s guesses are correct are partly independent from each other. Now, they’re not unconditionally independent: learning that most of Calvin’s 80%-opinions were false should make you suspect the (average) rational credence is lower than 80%, and thereby should shift your opinions in his other guesses. For the case to be analogous to Bianca’s, it needs to be the case that such shifts only happen through shifting your opinion about the rational credences. (Analogy: learning that one coin landed heads might shift your credence in whether another will, but only by shifting your opinion about the biases of the coins.) Put another way: information about the rational credences screens off Calvin’s guesses from each other; so conditional on the average rational credence being x, you treat the gi as independent. Precisely:
The right-and-rational inference fails in the misprinted coins case (Case 4, page 5) because Independence fails: we know that if one toss lands heads, they all will.Independence: Given that the average rational confidence for Calvin to have in his 80%-opinions is x%, learning that certain of these opinions are true or false shouldn’t affect your opinion in the others. For all
Does Independence hold in Calvin’s case? There’s much more to be said, but it’s well-motivated as a first approximation if the test questions were random and unrelated.18
Fact: when Deference and Independence hold, you should initially be confident that the average rational credence () is close to the proportion-true (), i.e. that the y-axes in Figure 1 align: is high. Thus so long as no evidence you get from the outcomes of the test defeats this expectation, you are warranted in performing the right-and-rational inference.
Why do you initially expect and to align? Because Deference and Independence make the case analogous to Bianca’s: ‘(average) rational confidence for Calvin’ plays the same epistemic role for you as ‘(average) bias of Bianca’s coins.’ In particular, conditional on Calvin’s 80%-opinions being on average rational, you should think it quite likely that roughly 80% of them will be true; and conditional on his 80%-opinions being on average quite overconfident (say, the average rational confidence is 60%), you should think it quite likely that less than 80% (roughy 60%) of them will be true. Since things are evidence for the hypotheses that make them likely, it follows that learning that 80% of his opinions are true is strong evidence that the (average) rational confidence was 80% (he was rational); meanwhile, learning that 60% of them are true is strong evidence that the (average) rational confidence was less than 80% (he was overconfident).
Toy example: suppose Calvin has 50 different 80%-opinions, and you’re initially equally confident that the average rational credence () is any of 60%, 61%,…, or 99%. Say he is substantially overconfident if the average rational confidence in his 80%-opinions is less than 75% (). Then if you learn that 70% of those opinions are true (), the right-and-rational inference is warranted: your credence that he’s substantially overconfident should jump from 37.5% to 78%. (See Appendix B.)
Upshot: the right-and-rational inference can be put on a firm theoretical foundation. Before learning about the outcomes of the test, you should often obey Deference and Independence, hence should be confident that proportion-true () will be a good guide to average-rational-credence is high.
But by the same token, this foundation also reveals why the right-and-rational inference is fragile. For when you get more evidence E about the outcome of the test—as you always will—that evidence may defeat your initial confidence in the alignment of proportion-true and average-rational-credence: although is high, it might be that becomes low. Such evidence might come in the form of how ‘tricky’ Calvin thought the test was, or how often his guesses overall were correct (§§4–5).
Why is this a problem? Suppose you learn something E about the test which satisfies two constraints:
-
1)
E does not significantly shift your opinions about whether Calvin’s 80%-opinions are rational: , for various t. And yet,
-
2)
E systematically distorts Deference: either for most gi and t, , or for most gi and .
Toy example: again suppose Calvin has 50 different 80%-opinions, and you’re initially equally confident that the average rational confidence () for him to have is any of 60%, 61%,…, or 99%. Then (by (1)) learning E doesn’t itself shift your opinions about , but since it tempers your deference downward by 10% (e.g. ), it changes how your should react to information about calibration. In particular, if you learn that 70% of those opinions are true (), you should (given E) decrease your credence that he’s substantially over-confident () from 37.5% to 22%, and increase your credence that he’s approximately rational () from 27.5% to 61%. The right-and-rational inference is inverted.
What does this mean for calibration studies? In order to make the case that the right-and-rational inference is warranted in a particular study, we must do two things. First, with must argue that Deference and Independence hold for our priors before giving the test. And second, we must argue that learning about the test-outcomes has not provided us with any information E that satisfies (1) and (2) above, i.e. information systematically distorts Deference without providing evidence about rationality. The first step is relatively straightforward and has become common practice: researchers try to ensure that subjects know everything we do about the test going into it. But the second step is not commonly addressed.
In §4, I’ll argue that this is a problem. There is a type of information that we almost always receive which does satisfy (1) and (2). That information is the hit rate: how often Calvin’s guesses were correct on the test as a whole. §5 then argues that although such information introduces expected rational deviations from calibration, these deviations are often predictable—hence a more nuanced version of the rational-and-right inference is still warranted.
4. The Limits
If we learn information E which both (1) does not itself affect our opinions about our subjects’ rationality, but (2) systematically distorts Deference, then the right-and-rational inference is liable to be unwarranted. In this section I’ll argue that this is a serious problem for real-world calibration studies.
Consider Calvin’s hit rate: the proportion of his answers on the whole test (not just his 80%-opinions) that are true. When we perform a calibration study, this is a piece of information we almost always receive. I’ll argue that—at least on binary-question tests—very often (1) such hit-rate information does not itself provide evidence about rationality (§4.1), and yet (2) it systematically distorts Deference.
4.1 Hit rates don’t provide evidence about rationality
Calvin’s hit rate is the overall proportion of his guesses—the things he’s greater than 50% confident in—which are true. This (of course) is determined by his calibration at each level of confidence (60%, 70%,…) weighted by how many opinions are in each group. I’ve argued above that, absent defeaters, the latter provide evidence about his rationality: learning that only 60% of his 80%-opinions are true provides reason to think he’s overconfident. Nevertheless, I’ll now argue that learning his overall hit rate in itself usually does not provide us with evidence about whether he’s overconfident.
How could this be? Structurally, there’s nothing odd about it. Learning how many birthdays I have between January 1 and July 31 (namely, 1) tells you something about when my birthday is; learning how many birthdays I have between January 1 and December 31 does not. Likewise: learning that 60% of Calvin’s 80%-opinions were true tells you something about his rationality; but learning that 60% out of all of his (50–100%-)opinions are true need not.
More specifically: Calvin’s hit rate is determined by his guesses, i.e. how often he’s more than 50% confident in true answers. Whether he’s overconfident is determined by his sorting of those guesses into various levels of confidence, i.e. whether once he decides to be more than 50% confident of gi, he raises his confidence to the appropriate level (R(gi)), or raises it too much (C(gi) > R(gi)) or too little (C(gi) < R(gi)). We might well have reason to think he’ll do the first part rationally (deciding which way to guess), while wondering whether he’ll do the second part rationally (deciding how confident to be in that guess). If so, hit-rate information shouldn’t shift our opinion in his rationality, while calibration information should.
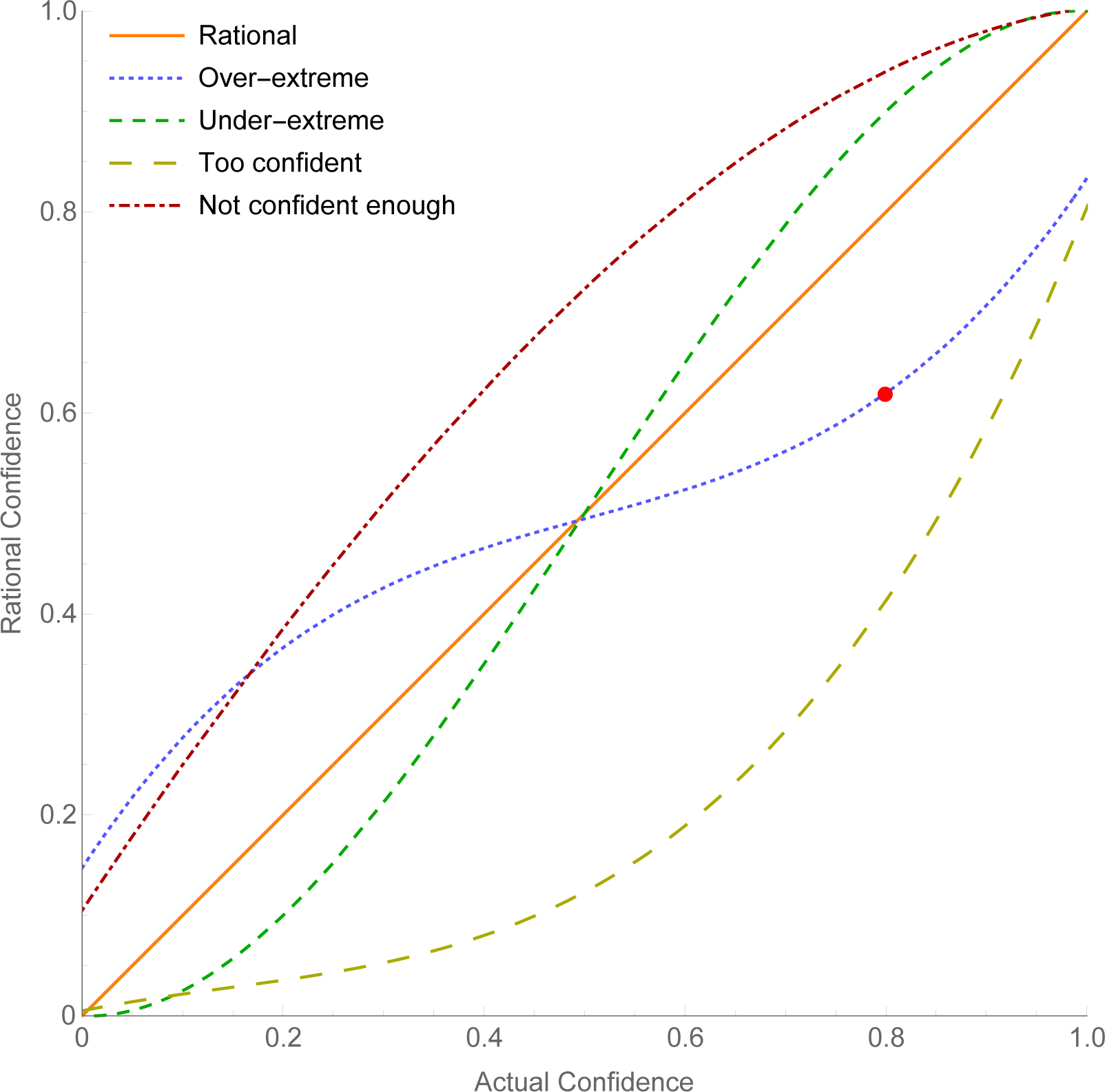
Indeed, the consensus in the literature is (perhaps inadvertently) committed to thinking this is our epistemic position. Here’s why. So far we’ve been focusing on the ‘overconfidence effect’—but in fact many studies find wildly different calibration curves for different sets of questions. Sometimes people are over-calibrated at all levels of credence; other times they are over-calibrated at high credences and under-calibrated at low ones; and so on. Translating these calibration curves to corresponding hypotheses about (ir)rationality, the varying shapes of possibilities are shown in Figure 2. Interpret the lines as averages: for example, the ‘over-extreme’ hypothesis says that when a person’s actual confidence is 80%, the confidence it is on average rational for them to have is merely 60% (as indicated by the red dot). The live (ir)rationality hypotheses in the literature are all of the form, ‘For claims of type X, people’s confidence obeys (ir)rationality hypothesis Y’, where X is some specification of question-type and Y is a curve with a shape similar to one in Figure 2 (Koehler et al. 2002; Brenner et al. 2005). The key point of agreement: all such hypotheses have a positive slope; higher credences correspond (on average) to higher rational credences. These are the live hypotheses because, empirically, higher credences always correspond, on average, to higher proportion-true.
Notice a prediction of any such hypothesis: when the alternative claims that someone is guessing between are of the same type, then people’s guesses on binary-questions will tend to be rational. Why? Take any such (ir)rationality hypothesis, and consider a guess between two claims q and q′—say, ‘Which is bigger: Denver or Phoenix?’ Suppose he’s more confident in the former: C(Denver) > C(Phoenix). Then the hypothesis predicts (from its positive slope) that, on average, it will be rational for Calvin to be more confident in the former: that R(Denver) > R(Phoenix). Hence he’ll guess the way he would if he were rational.20
What does this mean? Let H be Calvin’s actual (overall) hit rate on the test, i.e. the proportion of all his guesses that were true. Let RH be the hit rate that’s rational for Calvin to have, i.e. the hit rate he would’ve had if all his credences had been rational and he had guessed accordingly. All live (ir)rationality hypotheses predict that—on binary-question tests where all answers are of the same type—these two quantities are close, so P(H ≈ RH) is high. And none of them predict that this relationship will be modulated by how confident Calvin should be in (say) his 80% opinions, thus .
It follows that condition (1) holds: learning Calvin’s hit rate (H = s) does not itself provide evidence about what the rational opinions for Calvin are: , for various s and t. After all, learning Calvin’s hit rate (H) is more or less the same as learning the rational hit rate (RH), and clearly the latter would not tell you anything about whether Calvin is overconfident!
4.2 Hit rates distort Deference
Although (1) hit rates don’t provide direct evidence about Calvin’s rationality, I’ll now argue that (2) they do systematically distort Deference. In particular, learning that Calvin’s hit rate is abnormally low should lead you to expect that even if he’s rational he’ll be over-calibrated—meaning over-calibration will not necessarily be evidence for irrationality.
The reason is simple enough: learning Calvin’s hit rate gives you information that he didn’t have when he formed his opinions, and so which couldn’t have factored into the rational opinions. Absent such information, you should defer to Calvin’s rational opinions: given that he’s rational to be 80% confident in the gi, you should be 80% confident in each . But what about when you learn his hit rate? Take an extreme case: you learn that his hit rate is 0%, i.e. none of his guesses were true. Should you still expect that if he’s rational, 80% of his 80%-opinions will be true? Of course not—you know that none of them will be true: . Thus even if he’s rational (even if ), he’ll be over-calibrated ().
This is an extreme case, but the same reasoning works generally. If you learn that Calvin’s hit rate is lower than you expected before giving him the test, this will distort Deference by tempering your conditional opinions away from the rational credence and toward the hit rate. That is, often Deference will hold absent defeaters, but will fail when hit-rate information is added:
(When is H ‘low’? When it’s lower than you and Calvin were rational to expect before the test. Since 75% is the average of 50 – 100%, ‘how far H is below 75%’ is often a reasonable measure for how ‘low’ H is.)Upshot: hit rates cause a problem. As we saw at the end of §3, the right-and-rational inference is liable to be unwarranted when in performing the test we learn something that is both (1) not direct evidence about rationality, but (2) systematically distorts Deference. I’ve argued that in binary-question tests, hit rates often satisfy both these criteria. As a result, when we learn that subjects’ hit rates deviated far from what we (and they) should’ve expected going into the test, we should expect that even if they’re rational they won’t be calibrated. Thus we must be cautious in making inferences about their rationality in such settings.
But how cautious? And what else can we do? These qualitative concerns raise a quantitative question: how much deviation from calibration should we expect from rational people when hit rates vary?
5. The Implications
When we learn that hit rates are what we initially expected, the right-and-rational inference is warranted. But when the hit rates turn out to be surprisingly high or low, often it’s not: we cannot evaluate whether people are overconfident simply by checking whether they’re calibrated.
What should we do instead? My proposal is that we use simulations of the Bianca scenario to predict the rational deviations from calibration given our test setup, and then compare observed calibration curves to those predictions.21 Three steps:
-
1)
Model the test-construction procedure and form a hypothesis about the degree to which this procedure will lead to deviations from Deference and Independence.
-
2)
Translate that hypothesis into the Bianca analogy and use it to build a simulation of the rational opinions.
-
3)
Compare the predicted calibration curves for rational opinions from this simulation to the actual calibration curves we observe.
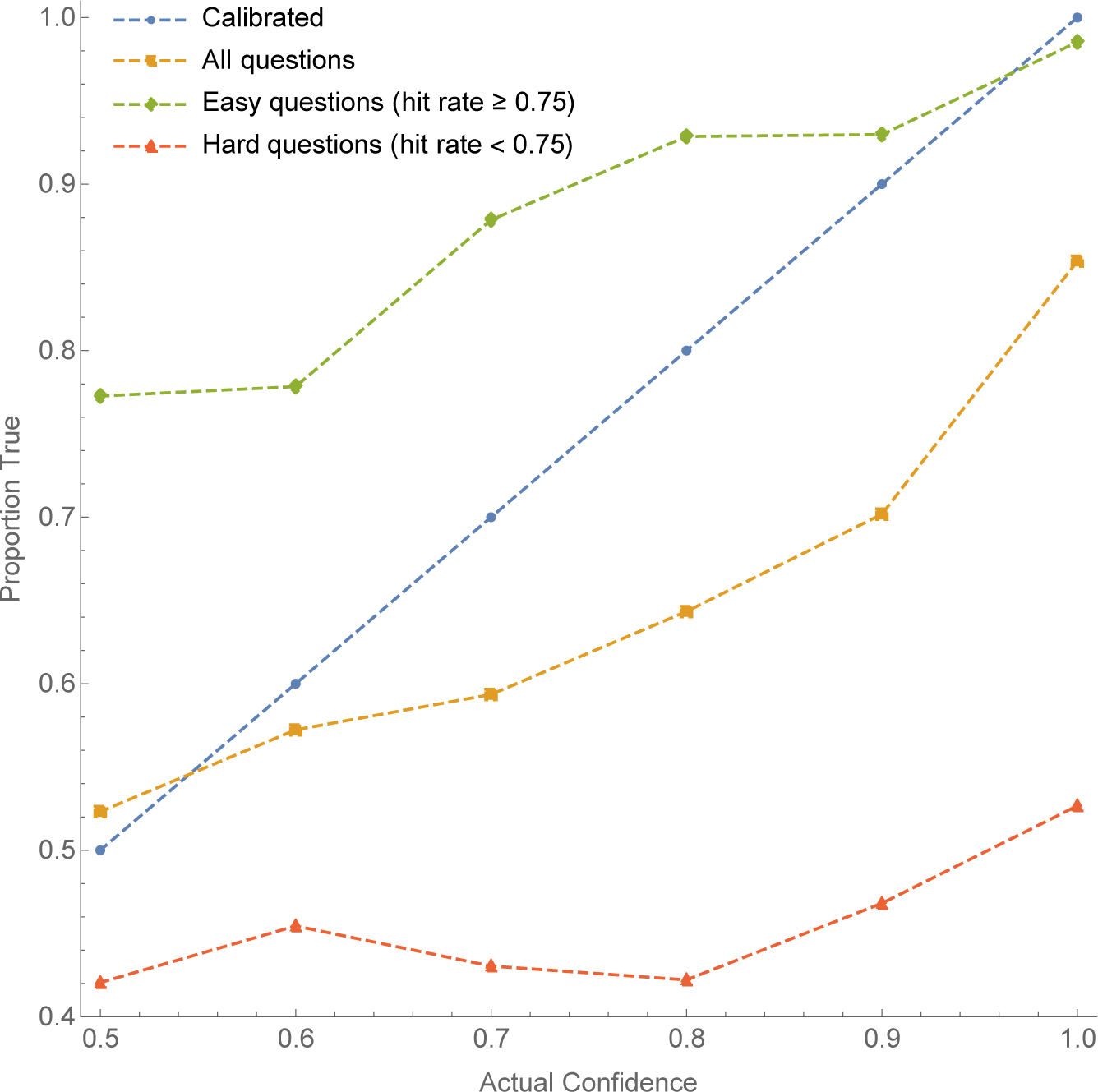
Studies do not always find the ‘overconfidence effect’. Rather, we can distinguish tests that are hard from those that are easy based on the hit rate: an easy test is one with a hit rate of at least 75%; a hard test is one with a hit rate of less than 75%. The empirical generalization that subsumes the ‘overconfidence effect’ is called the hard-easy effect: people tend to be over-calibrated on hard tests and under-calibrated on easy tests—see Figure 3. The hard-easy effect has been called ‘fundamental bias in general-knowledge calibration’ (Koehler et al. 2002, 687), the idea being that people do not sufficiently adjust for task-difficulty, leading them to be overconfident on hard tests and underconfident on easy ones. This effect is widely cited as one of the core pieces of evidence in favor of irrational explanations of miscalibration.22
At this point we should have some skepticism about this claim. As we saw in §2, we should always expect (even perfectly rational) people to be over-calibrated on ‘the set of guesses they got wrong’ and under-calibrated on ‘the set of guesses they got right’ (cf. Juslin et al. 2000). Thus when we divide the questions on a given test into those that people tended to get wrong (questions with a low hit rate) and those that they tended to get right (questions with a high hit rate), we risk distorting Deference in a way that undermines the right-and-rational inference. And moreover, even when we do not divide questions after the fact, we saw in §4 that for tests on which the hit rate was surprisingly low or high, we often should expect rational people to deviate substantially from calibration.
So what are we to do? How can we get evidence about whether the degree to which people exhibit the hard-easy effect is more or less than we’d expect if they were rational? My proposal is that we can get a handle on this by thinking through versions of the Bianca scenario. Assume that she can (on average) decipher the tablet markings—setting her confidence equal to the biases of the coins, on analogy with Calvin being rational—and go on to simulate what calibration curves we should expect from her as we vary the hit rate.
Step 1 is to form a model of our test-construction procedure, along with a hypothesis about the degree to which Deference and Independence hold—and hence whether and how robustly we should expect the rational opinions to be calibrated. For illustration, focus on the simplest case: a test on which we can reasonably suppose that Deference is quite robust. One way to try to form such a test is to pull questions randomly from a well-defined, representative domain on which we can expect that the accuracy of people’s evidence will not be systematically correlated across questions. This turns out to be a difficult criterion to meet, but I’ll take a standard paradigm from the literature (Gigerenzer et al. 1991), pulling pairs of American cities randomly from the top-20 most populous cities, and asking people which they think has a bigger population. (How robust your Deference is here is a vexed question we’ll return to; for the moment, assume it’s very robust, i.e. Independence holds fully).
Given this, we can perform Step 2: simulate our test using the Bianca analogy. We toss a number of coins (equal to the number of questions on our test), selecting them uniformly at random from coins of varying biases between 50–100%23, have her guess how they’ll land and rate her confidence in that guess, and record her calibration curve. This is a single trial. Repeat thousands of times, and now look at the average results on trials (sets of questions) that have various hit rates. What do we expect to see?
For all simulations, I’ll display two versions. The perfection model assumes Bianca always gets the biases of the coins exactly right (analogy: Calvin is always perfectly rational). The noise model assumes that Bianca’s announced confidence is a random perturbation of the bias of the coin—capturing the idea that she may be reliable but imperfect at deciphering the coins’ biases (analogy: Calvin’s confidence may be a reliable but imperfect tracker the rational confidence).24 The most plausible rationality hypotheses are ones in which there is some such error, meaning subjects aren’t fully rational (cf. Brenner 2000), but merely approximately so.
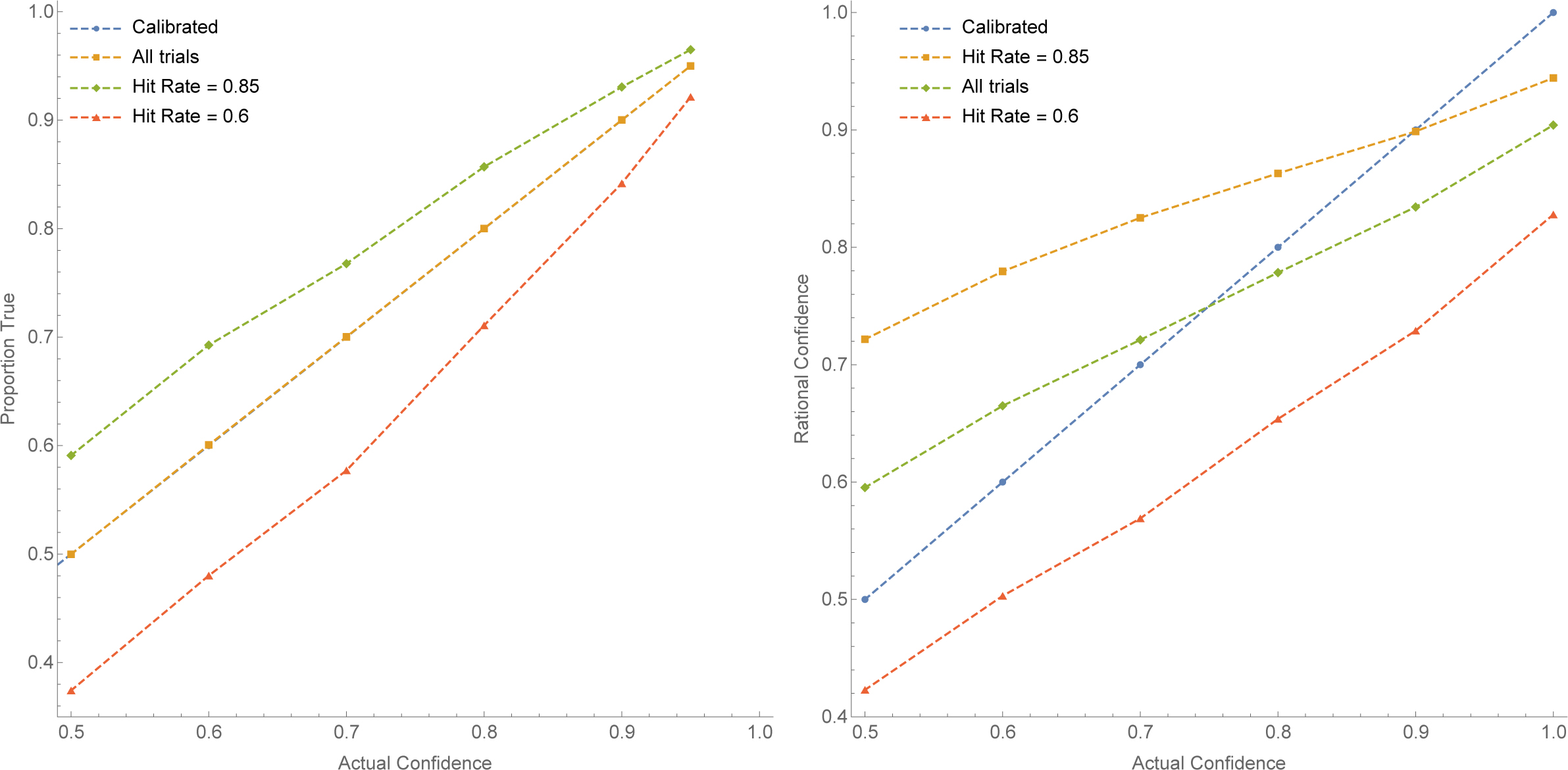
For illustration, the expected calibration curves for Bianca at various hit rates are displayed in Figure 4. When we consider all trials together, Bianca is calibrated. Perfectly calibrated in the perfection model. Slightly less calibrated in the noise model due to ‘scale-end effects’ (Juslin et al. 2000), since at the end-points of the confidence scale errors can only go in one direction, resulting in the tilting of the curve. But among tests where the hit rate is low (high), Bianca tends to be over- (or under-) calibrated—just as observed empirically with the hard-easy effect.
Let’s pause and emphasize that: even if Calvin were perfectly rational (even if Bianca can perfectly decipher the coins), we’d expect to observe a version of the hard-easy effect. Why? Consider a given trial on which the proportion of heads was lower than usual. Why was it lower? One hypothesis is that this trial had an abnormally large proportion of coins that were biased against landing heads. An alternative hypothesis is that more of the coins landed tails than you’d usually expect given their biases. Absent further information, both are likely to play a role in any given trial with a low hit rate. Bianca will account for the first factor in setting her degrees of confidence, since she can recognize the coins and see that more of them than usual have a low bias—but she can’t account for the second factor. Thus as we consider cases with more extreme hit rates, Bianca becomes increasingly miscalibrated. For example, take the perfection model—where Bianca is as sensitive to the biases of the coins as she could possibly be. On trials with a hit-rate of 75%, Bianca’s average confidence was 75%; on trials with a hit rate of 90%, her average confidence is 77% (becoming under-calibrated); and on trials with a hit rate of 60%, her average confidence is 72.7% (becoming over-calibrated).
Upshot: even in the best-case test-construction scenario, we should still expect some form of the hard-easy effect to emerge for rational subjects. Moreover, if they are merely approximately rational (the noise model), we should expect rational calibration curves that are qualitatively similar to the curves often observed empirically. Thus the hard-easy effect in itself is not clear evidence of irrationality.
Let’s now perform Step 3 and apply this model to my study (pre-registration available at https://aspredicted.org/rq7cu.pdf). (This experiment is intended only as a proof of concept; to give a proper empirical assessment of the hard-easy effect would require more systematic and sophisticated empirical and statistical methods.)
I generated all pairs from the 20 most-populous U.S. cities, and recruited 200 U.S. residents through Prolific (90 F, 107 M, 3 Other; mean age 34.7). After giving them standard instructions about how to use the 50–100% confidence scale, I presented each with 21 pairs—20 randomly selected from the 190 pairs, and 1 attention check. (I excluded the 1 participant who failed the attention-check.)
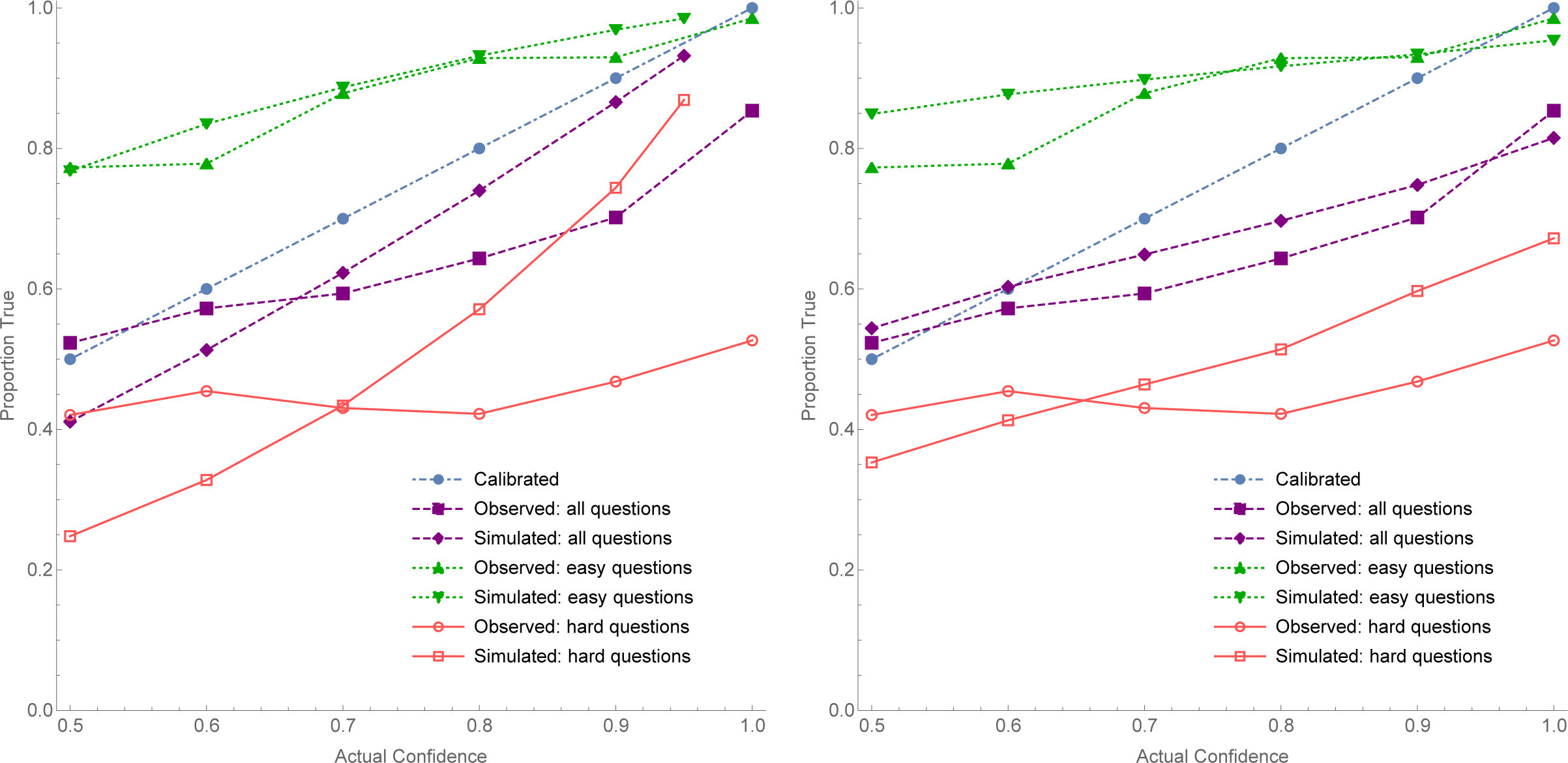
I pooled subjects’ answers, and divided the questions into those that were easy (more than 75% of answers correct) and those that were hard (less than 75% correct). Figure 3 (page 15) above shows the calibration curves from my study overall, among the hard questions, and among easy ones. The hard-easy effect was observed as expected—though it was especially stark. among hard questions the average confidence was 75.1%, while the proportion true was only 45.2%.25 Meanwhile among easy questions, the average confidence was only 84.7%, while the proportion true was 92.1%.26 Unexpectedly, the test overall was slightly hard, with an average confidence of 79.8% and a proportion true of only 68.0%—hence the over-calibration observed overall.27
We can compare these results to both the perfection model and noise model predictions of rational subjects. As pre-registered, these simulations were generated by setting the number of questions Bianca faces to the size of the easy/hard/all-questions set, simulating millions of trials, and then removing trials with high/low hit rates until the mean hit rate matched the actual hit rate in the easy/hard/all-questions sets. The perfection model has no free parameters; its comparisons to the data from my study are displayed on the left of Figure 5. Though the predicted rational curves deviate substantially from calibration, they have steeper slopes than the empirically-observed ones. This indicates that if this is a good model of the test-construction procedure, real subjects deviated substantially from perfect rationality (though not as far as comparison with the calibrated line would suggest).
Meanwhile, the noise model has a free parameter for the standard deviations from rational confidence. As pre-registered, the simulations were run with the parameter varying from 0–0.3, and the parameter was chosen to minimize mean squared divergence between the model predictions and the actual curves. This set the noise parameter to 0.3, and the resulting comparison between simulations and the data in my study is displayed on the right of Figure 5. The predictions generated from the rational-credence-plus-noise model are generally close to the observed miscalibration, indicating that the data provide evidence for this (ir)rationality hypothesis. Notice that while this hypothesis says that people are on average rational, the large noise parameter (0.3) is one on which they deviate substantially in any particular case (cf. Brenner 2000).
But there’s an issue with this hypothesis. This model and simulation assumed Deference was quite robust, i.e. Independence held fully. Looking at the empirical data, this seems implausible. It was incredibly difficult to find simulation-runs leading to hit rates as extreme as observed in the real study (of 8 million trials, only 183 had hit rates at or below 0.515, while my study’s hard questions had a hit rate of 0.452). Statistically, this is due to the fact that given Independence, it is very hard for a question-set of this size to deviate substantially from a 75% hit rate. However, if Independence fails—meaning when some guesses are wrong, others are more likely to be as well—such deviations are much more common. Indeed, it’s natural to think that Independence does fail on this city-comparison test, due to the fact that the questions share a common subject-matter.28 If someone is mistaken about one question, that should increase our credence that they’ll be mistaken about others. (Recall Georgie: if she’s wrong about several geographical opinions, we should think it more likely that she’ll be mistaken about others.)
In particular, even if we should expect that the opinions warranted by people’s evidence will on the whole be calibrated, we should also expect that there will be random fluctuations in how calibrated they are across subject-matters. For instance, in my city-comparison test, some participants will have evidence that warrants misleadingly strong opinions (only 70% of the opinions they should be 80% confident in are true), while others will have evidence that warrants misleadingly weak opinions (90% of the opinions they should be 80% confident in are true). Moreover, these fluctuations in evidence will likely be correlated for a given person on a given subject-matter—if only 50% of the opinions Calvin ought to be 60% confident in on my test are true, we should expect that (say) only 60% of the ones he ought to be 70% confident in are true.
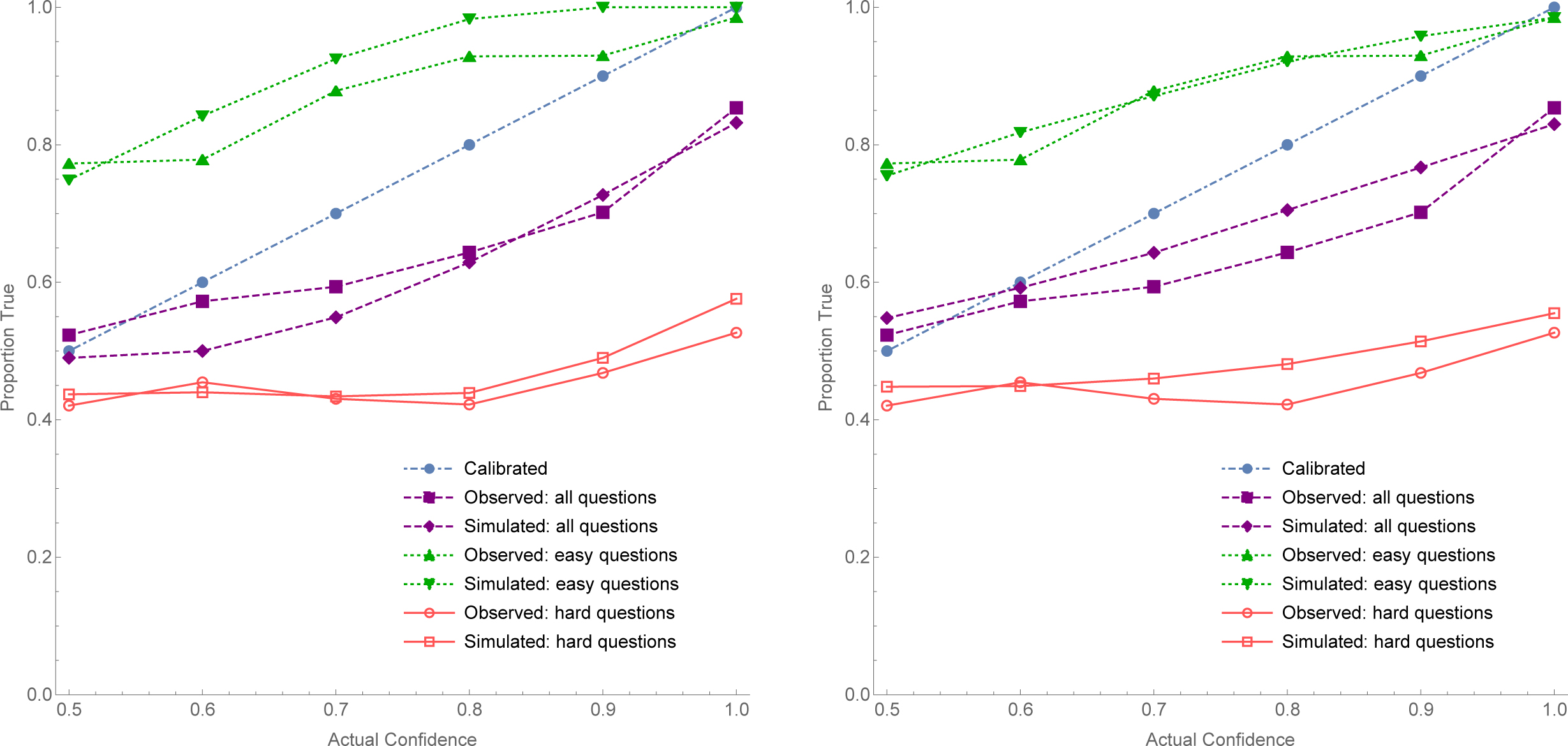
Here’s a simple model of the test-construction procedure—an alternative to the one given above. Again, there is a random number of coins of varying biases, and Bianca correctly deciphers them. But this time there is random variation across tablet-archives in how representative they are of the broader distribution of tablets—some archives have higher proportions of heads than would be expected given the bias; others have lower proportions. Thus for each trial (visit to an archive), we generate a random misleadingness parameter and add it to the coin biases to determine how far the proportion of heads in this archive deviates from the biases of the coins.29
Although I had constructed these models before running my city-calibration test, it only occurred to me that they were an apt model of it after running the test and seeing how extreme the variation in hit rates were. (The empirically-observed curves looked familiar…) As a result, these comparisons were not pre-registered and should be taken with several grains of salt. But it turns out to be much easier to find hit rates as extreme as the ones we observed using this model, lending the model some support. Running the same analysis as above yields the optimal noise parameter at 0.15, and yields the comparisons in Figure 6. These curves fit the data well, meaning that the hypotheses that generated them—namely, misleadingness varies but subjects are rational—are supported by it. (But your priors in this model should be adjusted by, among other things, the fact that they were not pre-registered!)
These results are preliminary. Nevertheless, qualitative effects like the hard-easy effect are predicted—and when we incorporate the possibility of either noise in subjects’ judgments or random misleadingness in subjects’ evidence (or both), the observed calibration curves are close to what we should expect from rational people. It is the (much smaller) deviations from these predicted curves that we must study systematically—not the deviations between people’s actual confidence and the perfectly-calibrated line.
6. More Questions
I’ll close by considering how this theory of rational (mis)calibration depends on the philosophical tenability of Deference (§6.1), as well as its implications for other forms of calibration studies (§6.2).
6.1 The Tenability of Deference
Deference is the crux of the right-and-rational inference. But, as discussed in §3, Deference is the strongest tenable interpersonal deference principle—and there are many reasons to be worried about it. First, if epistemic rationality is permissive, then you may have different epistemic standards than Calvin (White 2005; Schoenfield 2014, 2019). If so, the fact that his standards rationalize being 80% confident in q doesn’t imply that your standards do. Perhaps your standards warrant being systematically more cautious (less extreme) in your opinions than Calvin’s do. If so, Deference will fail. Open question: can permissivists justify the right-and-rational inference, even in the best-case scenarios?
Similarly, if epistemic modesty can be rational—if it can be rational to be unsure of what opinions are rational—then Deference must sometimes fail (Christensen 2010b; Elga 2013; Dorst 2020a). The only deference principle I know of that is both tenable in the case of modesty, and would warrant a variant of the above reasoning from §3 is a version of the ‘Trust’ principle in Dorst 2020a, formulated in Dorst et al. 2021.30 Other approaches to modesty (Elga 2013; Pettigrew and Titelbaum 2014; Lasonen-Aarnio 2015; Williamson 2019; Gallow 2021) allow arbitrarily large deviations from Deference. Open question: can they justify the right-and-rational inference, even in simple scenarios?
6.2 Dunning-Kruger and Overprecision
I’ve focused on binary-question tests, but there are a variety of other ways to measure calibration. My arguments raise two salient questions about them: (1) given that tests can be hard even for rational people, to what degree should we expect rational people to be calibrated? And (2) to the extent that such tests involve guessing, what should we expect (rational) people to guess?
(1) First, the fact that we should often expect rational people to be over-calibrated has implications for both the Dunning-Kruger effect (Kruger and Dunning 1999) and the finding of ‘over-precision’ (Moore et al. 2015b).
The Dunning-Kruger effect is the finding that the gap between a person’s relative performance on a test and their estimate of this number grows as their performance decreases. For example, those in the 50th percentile estimate that they’re in the 60th, while those in the 20th estimate they’re in the 50th. This is often thought to indicate irrationality (Dunning 2012). But we’ve seen that for any set of (rational) opinions, some tests will be hard (have low hit rates)—and that as the test gets harder, the gap between hit rate and estimated hit-rate grows (§5). This supports the rational models of the Dunning-Kruger effect proposed by Moore and Healy 2008 and Jansen et al. 2018 (but see Jansen et al. 2021).
Meanwhile, over-precision is often found on interval-estimation tests: ask people to give confidence intervals for the true value of some unknown parameter, like the length of the Amazon. People tend to be quite ‘over-precise’ in the sense that their 90% confidence intervals standardly miss the true value as much as 50% of the time. Some take this to be better evidence for overconfidence than the over-calibration found in binary-question tests.31 Although this may be correct, translating between interval- and binary-question tests (Tversky and Kahneman 1974) gives me pause: Calvin’s 90% confidence interval for the length of the Amazon is ‘1000–5000 miles’ iff he’s 95% confident in both ‘It’s at Least 1000’ (L) and ‘It’s at Most 5000’ (M). Thus we should expect a rational miss-rate of 50% iff, given our background information, P(L&M) ≈ 0.5. This does not seem implausible. According to our simulations (Figures 4, 5, and 6), on hard tests we should expect no more than (and often much less than) 75% of people’s 95%-opinions to be true, i.e. P(L) ≤ 0.75 and P(M) ≤ 0.75. Thus if L and M were independent, we should expect a miss-rate of at least 44% (1 − 0.75 · 0.75 ≈ 0.44). Yet, by definition, L and M are not independent: if L is false, M must be true; thus L being true makes M less likely, meaning we should expect even higher miss-rates—50% is not surprising.32
(2) Finally, my analysis of binary-question tests has relied on the (standard) assumption that people will guess the answer they think is most likely. But for questions with more than two complete answers, the relationship between (rational) credences and guessing turns out to be much more complicated than this (Kahneman et al. 1982; Holguín 2022; Dorst and Mandelkern 2022; cf. Horowitz 2017)—sometimes it makes sense to guess an answer that’s improbable so long as it’s specific (informative) enough (cf. Levi 1967). I don’t know how exactly this will affect the analysis of other cases, but it does raise the question of what we should expect rational people to guess in contexts—like interval-estimation tests—in which the question under discussion is not a binary one. In particular, it shows that in order to perform the right-and-rational inference, we must either provide evidence that people do not guess the way they would if they were rational, or else control for expected rational deviations from calibration due to rational variations in hit rates, as I’ve done here.
7. The Upshot
Many have taken the results of calibration studies to demonstrate that people tend to be systematically overconfident in a way that is both dire and preventable. I’ve argued that the theoretical foundations of this inference are shaky (§2), but that we can secure them by articulating a probabilistic connection between being rational and being right (§3). However, doing so reveals a methodological flaw: no matter how well-designed the study or how rationally people form their opinions, they should still be expected to be miscalibrated in systematic ways (§4). I used this result to propose an amended methodology: we must use information about our study (including hit rates and potential failures of Independence) to predict the rational deviations from calibration, and then compare people’s performance to those predictions. I illustrated how this can be done, and argued that it complicates the standard interpretation of robust empirical effects (§§5–6).
If even a portion of this discussion is correct, it suggests that certain debates in philosophy and psychology are much closer than has been realized. Psychologists have had a spirited debate about the bearing of empirical results on human rationality33—yet most contemporary philosophical debates about rationality have been relatively isolated from these issues (but see footnote 7). As we’ve seen, these debates bear on each other. Whether and to what extent we have empirical evidence for overconfidence depends on the connection between being rational and being right, which in turn depends on philosophical debates about the nature of evidence, deference principles, permissivism, and epistemic modesty (§3, §6.1). Conversely, calibration studies bring to the philosophical literature the idea that there is an evidential connection between being rational and being right (§3), and that simulation methods can be used to make precise predictions about this connection (§5).
In short: the questions and methods from both philosophical and psychological investigations of rationality can be tied together in surprising and fruitful ways. If we continue to bring these investigations closer together, what other ties might we find?34
Appendix A. Deriving Deference
Recall that g1, …, gn are the claims that Calvin assigns 80%-confidence to, that R is the rational probability function for him to have overall, and that is the average rational confidence in the . Recall Deference:
(For simplicity I focus on Calvin’s 80%-opinions; the reasoning generalizes.)Deference: For all .
Assuming that R is a probability function, Deference follows from two principles:
Since Equality is plausible in the situations we’re considering (all you know about the gi is that they were claims that Calvin was 80% confident in), this shows that Deference follows from the more familiar Point-wise version.Point-wise Deference: For all gi: P(gi|R = δ) = δ(gi).35
Equality: For all .
To prove this, for any random variable X, let be your rational expectation of X. Note that is a random variable; also note that if is the indicator variable for gi, then . Let Dx = {δ1, …, δk} be the set of possible values of R such that , so that .
Consider your expectations of the proportion of truths conditional on :
By linearity of expectations, this equalsTherefore , so by linearity of expectations, your average rational credence in the gi equals . By Equality, since each of the values in this sum is equal, they must all be equal to x, establishing Deference.
Appendix B. The Right-and-Rational Formula
Here I show how to calculate what your posterior confidence should be that Calvin is overconfident in his 80%-opinions when (i) Deference and Independence hold, (ii) you know that there are n such opinions, and (iii) you learn how calibrated they are. Recall:
Suppose you initially leave open that will be any of t1, …, tm, with prior probabilities . Note that Deference and Independence imply that treats the gi as i.i.d. Bernoulli variables with success probability ti. Letting be the proportion of gi that are true, that means that conditional on , is distributed according to a binomial distribution with parameters ti and .Deference: For all .
Independence: For all :
Now suppose you learn that proportion s·n of the gi were true. By Bayes formula, your posterior confidence in any hypothesis should be:
Notes
- See §5 for details and discussion. Answers: Phoenix, San Jose, Columbus. ⮭
- E.g. Lichtenstein et al. 1982; Dunning et al. 1990; Vallone et al. 1990; Griffin and Tversky 1992; Kahneman and Tversky 1996; Budescu et al. 1997; Brenner 2000; Koehler et al. 2002; Brenner et al. 2005; Merkle and Weber 2011; Brenner et al. 2012; Moore et al. 2015b; Ehrlinger et al. 2016; Magnus and Peresetsky 2018. ⮭
- E.g. Plous 1993; Fine 2005; Ariely 2008; Hastie and Dawes 2009; Myers 2010; Kahneman 2011; Thaler 2015; Lewis 2016; Tetlock and Gardner 2016. ⮭
- E.g. Howard 1984; Odean 1999; Glaser and Weber 2007; Johnson 2009; Johnson and Fowler 2011; Ortoleva and Snowberg 2015; van Prooijen and Krouwel 2019. ⮭
- Shariatmadari 2015. A minority of authors argue that the ‘overconfidence effect’ is compatible with rationality (e.g. Gigerenzer 1991; Hoffrage 2004; Angner 2006; Moore and Healy 2008; Benoît and Dubra 2011)—see §2. ⮭
- For philosophical discussions, see Joyce 1998; Littlejohn 2012, 2018; Gibbons 2013; Schoenfield 2016; Horowitz 2014b, 2019; Wedgwood 2017; Lord 2018; Rinard 2019; Comesaña 2020; Staffel 2020. ⮭
- E.g. Kelly 2004, 2008; Crupi et al. 2008, 2009; Fitelson and Hawthorne 2010; Koralus and Mascarenhas 2013; Nebel 2015; Icard 2018; Mandelbaum 2018; O’Connor and Weatherall 2018; Hedden 2019; Singer et al. 2019; Doody 2020; Quilty-Dunn 2020; Dorst and Mandelkern 2022; Karlan 2021; Kinney and Bright 2021; Thorstad 2021; Dorst 2022. ⮭
- Swap the rest for their negations—people tend to satisfy complementarity (Wallsten et al. 1993), so if he’s less than 50% confident in q we’ll assume he’s more than 50% in ¬q. ⮭
- As a referee points out, this goes further than psychologists are committed to: it might be determinate what the average rational credence is in a set, but indeterminate what credence is rational to have in its individual members. Since the principles that drive my argument (‘Deference’ and ‘Independence’) apply to the average , rather than R(gi), the lessons should carry over. (There will be enough complexity as it is.) ⮭
- Including those cited in footnotes 2, 3, 4, and 5. Some studies invoke objective probabilities, true (vs. reported) confidence, or the confidence of differing agents (Gigerenzer et al. 1991; Erev et al. 1994; Juslin et al. 1997, 1999, 2000; Moore and Healy 2008). None of these can stand in for rational confidence. ⮭
- Some derive this result for a given Bayesian agent (Brenner et al. 2005; Moore and Healy 2008; Merkle and Weber 2011; Benoît and Dubra 2011; Benoît et al. 2015). But they assume that the Bayesian’s priors match the frequencies on the test. This can’t in general be assumed. ⮭
- Might this indicate that these studies aren’t interested in rationality? No. They’re filled with normative assessments of people’s opinions as ‘irrational’ (Hoffrage 2004, 245; Magnus and Peresetsky 2018, 2), ‘unjustified’ (Dunning et al. 1990, 579; Vallone et al. 1990, 588), ‘unreasonable’ (Merkle and Weber 2011, 264), ‘biased’ (Koehler et al. 2002, 686; Glaser and Weber 2010, 249; Moore et al. 2015b, 182), and so on. Kahneman and Tversky put it bluntly: ‘Our disagreement [with Gigerenzer 1991] is normative, not descriptive. We believe that subjective probability judgments should be calibrated, whereas Gigerenzer appears unwilling to apply normative criteria to such judgments’ (1996, 589). ⮭
- Let C be his probability function, be his expectation of any random-variable X (so , and be the indicator variable for q. Then his estimate for the proportion of gi that are true is . Moreover, if C treats the gi as independent, then as n grows, C becomes increasingly confident that . ⮭
- What about precedents in the philosophical literature? While many have addressed the connection between being rational and being right (footnote 6), to my knowledge none have addressed the right-and-rational inference (and interpretation of calibration studies) as formulated here. Regarding calibration, they’ve instead asked: whether calibration can ‘vindicate’ a set of opinions (van Fraassen 1983; Dawid 1983; Seidenfeld 1985; Joyce 1998; Dunn 2015; Pettigrew 2016); whether Bayesians’ beliefs about their own calibration are problematic (Dawid 1982; Belot 2013a,b; Elga 2016); or how your expectations about calibration should affect your credences (Roush 2009, 2016, 2017; White 2009b; Christensen 2010a, 2016; Lam 2011, 2013; Sliwa and Horowitz 2015; Schoenfield 2015, 2018; Isaacs 2021). ⮭
- Which have been criticized on various grounds (Kahneman and Tversky 1996; Budescu et al. 1997; Brenner 2000; Koehler et al. 2002; Brenner et al. 2005; Merkle and Weber 2011). ⮭
- Why are you in the picture at all? Whether Calvin is rational has nothing to do with you; but whether you have evidence that he’s rational does—and that is our question. For simplicity, I’ll assume that your rational opinions can be modeled with a precise probability function—but the reasoning will generalize. For discussion of the (de)merits of such models, see White 2005, 2009a; Schoenfield 2012, 2014; Horowitz 2014b; Schultheis 2018; and Carr 2020. ⮭
- Appendix A shows how the ‘averaged’ version follows from a more familiar ‘point-wise’ version. ⮭
- This is only partially right—for example, learning that all of Calvin’s other 80%-opinions were false should make you suspicious. What’s plausible is that the gi are exchangeable (order doesn’t matter) given . Exchangeability supports similar reasoning, and the closer the gi come to being independent, the better evidence (mis)calibration will provide about . ⮭
- Why do we need (1)? Because information can distort Deference without problematizing the inference if it does so by shifting your opinions about Calvin’s rationality. Consider calibration information itself: if you learn that that only 60% of his 80%-opinions were true, you should then be 60% in each gi regardless of what is (Deference fails); but this doesn’t mean the right-and-rational inference fails, since learning this may already have increased your credence that Calvin was overconfident (that ). ⮭
- Formally, let C(q) be Calvin’s actual confidence in q, and let an (ir)rationality hypothesis be a function f: [0, 1] → [0, 1] mapping actual degrees of confidence to (average) rational degrees of confidence: f(C(q)) = R(q). Any such function that is monotonically increasing (f(x) > f(y) iff x > y, i.e. has a positive slope) will be such that if R(q) > R(p), then f(C(q)) > f(C(p)), hence C(q) > C(p). Since f is an average, this allows individual guesses to sometimes be irrational. But if we use the average hit rate (across subjects) on a test—as experiments usually do—such deviations from rationality should cancel out, and the average hit rate should be close to the average rational one. ⮭
- The simulation of rational opinions to predict miscalibration was pioneered by Erev et al. 1994; Pfeifer 1994; and Juslin et al. 1997, 1999. What I’m arguing is that such simulations are not the special purview of those testing rational models of confidence-formation—rather, they are a necessary precondition for figuring out what results on our test would be evidence of overconfidence. ⮭
- E.g. Lichtenstein et al. 1982; Keren 1987; Gigerenzer et al. 1991; Griffin and Tversky 1992; Juslin 1994; Juslin et al. 2000; Koehler et al. 2002; Brenner et al. 2005; Hoffrage 2004; Moore and Healy 2008; and Glaser and Weber 2010. ⮭
- I simplify by tossing coins of biases 50–100% and having her always guess heads, rather than coins of biases between 0–100% and having her first guess heads or tails. The statistics are the same. ⮭
- I assume the errors are normally distributed with mean 0; Figure 4 uses a standard deviation of 0.2. This model takes inspiration from ‘error models’ (Erev et al. 1994; Pfeifer 1994; Juslin et al. 1997, 1999), but the interpretation is importantly different. Their models treat people’s reported opinions as imperfect indicators of their true opinions (or, in some cases, objective frequencies), whereas mine treats people’s reported opinions as imperfect indicators of the rational opinions. While tests of variance suggest that error in reporting true confidence cannot account for the observed miscalibration (Budescu et al. 1997), these tests don’t examine deviations between reported confidence and rational confidence. ⮭
- Average confidence in hard questions (M = 0.751, SD = 0.165) was above proportion true of hard questions (M = 0.452, SD = 0.498), with t(2487) = 25.82, p < 0.001, and d = 0.808 (one-sided). ⮭
- Average confidence in easy questions (M = 0.847, SD = 0.162) was below proportion-true of easy questions (M = 0.921, SD = 0.270), with t(3156) = 10.37, p < 0.001, and d = 0.333 (one-sided). ⮭
- Average confidence across all questions (M = 0.798, SD = 0.170) differed from proportion true (M = 0.680, SD = 0.467), with t(5013) = 14.97, p < 0.001, and d = 0.336 (two-sided). ⮭
- This is a common feature of calibration tests; see e.g. Dunning et al. 1990; Vallone et al. 1990; Brenner et al. 1996; Koehler et al. 2002; Brenner et al. 2005; Hoffrage 2004; Glaser and Weber 2007; Merkle and Weber 2011; and Brenner et al. 2012. ⮭
- In the displayed simulations this parameter is normally distributed with mean 0 and (for illustration) standard deviation 0.2. In these simulations I assume that the variation in misleadingness is only in the magnitude—not the direction—of the evidence, so it never pushes below 50%. ⮭
- The variant reasoning requires pooling people’s opinions into categories like ‘at least 60% confident’ (instead of ‘exactly 60%’) and seeing whether at least 60% (rather than exactly 60%) of them are true. ⮭
- E.g. Moore and Healy 2008; Glaser and Weber 2010; Ortoleva and Snowberg 2015; and Moore et al. 2015a,b. ⮭
- Since P(M|¬L) = 1 > P(M), P(M|L) < P(M). Thus if L lowers the probability of M by 10% (so P(M|L) ≤ 0.65), then P(L&M) ≤ 0.75 · 0.65 ≈ 0.49. ⮭
- For classic statements of the ‘irrationalist’ approach, see Tversky and Kahneman 1974, 1983; Kahneman et al. 1982; Kahneman and Tversky 1996; Fine 2005; Ariely 2008; Hastie and Dawes 2009; Kahneman 2011; and Thaler 2015. For defenses of ‘rational’ approaches see Anderson 1990; Gigerenzer 1991; Oaksford and Chater 1994, 2007; Tenenbaum and Griffiths 2006; Hahn and Oaksford 2007; Hahn and Harris 2014; Harris and Hahn 2011; Tenenbaum et al. 2011; Griffiths et al. 2012; and Cushman 2020. ⮭
- Thanks to Lyle Brenner, Liam Kofi Bright, Thomas Byrne, Fiery Cushman, Chris Dorst, Dmitri Gallow, Cosmo Grant, Brian Hedden, Thomas Icard, Priyedarshi Jetli, Joshua Knobe, Harvey Lederman, Matt Mandelkern, Don Moore, Daniel Rothschild, Bernhard Salow, Miriam Schoenfield, Ginger Schultheis, James Shaw, Jack Spencer, two tremendously-helpful referees, and audiences at FEW 2020, MIT, Fordham University, and the Universities of Bristol, Pittsburgh, Oxford, and Sydney, for much helpful feedback and discussion. ⮭
- Here ‘δ’ is a rigid designator for a particular probability function (an assignment of numbers to propositions), whereas R is a definite description for ‘the rational credence function for Calvin, whatever it is’—so R can vary across possibilities but δ cannot (see Schervish et al. 2004; Dorst 2019). ⮭
References
Anderson, John R, 1990. The Adaptive Character of Thought. Erlbaum Associates.
Angner, Erik, 2006. ‘Economists as experts: Overconfidence in theory and practice’. Journal of Economic Methodology, 13(1):1–24.
Ariely, Dan, 2008. Predictably Irrational. Harper Audio.
Belot, Gordon, 2013a. ‘Bayesian Orgulity’. Philosophy of Science, 80(4):483–503.
Belot, Gordon, 2013b. ‘Failure of calibration is typical’. Statistics and Probability Letters, 83(10):2316–2318.
Benoît, Jean-Pierre and Dubra, Juan, 2011. ‘Apparent Overconfidence’. Econometrica, 79(5):1591–1625.
Benoît, Jean Pierre, Dubra, Juan, and Moore, Don A., 2015. ‘Does the better-than-average effect show that people are overconfident?: Two experiments’. Journal of the European Economic Association, 13(2):293–329.
Brenner, L. A., Koehler, D.J., Liberman, V., and Tversky, A., 1996. ‘Overconfidence in Probability and Frequency Judgments: A Critical Examination’. Organizational Behavior and Human Decision Processes, 65(3):212–219.
Brenner, Lyle, 2000. ‘Should Observed Overconfidence Be Dismissed as a Statistical Artifact? Critique of Erev , Wallsten , and Budescu (1994)’. Psychological Review, 107(4):943–946.
Brenner, Lyle, Griffin, Dale, and Koehler, Derek J, 2005. ‘Modeling patterns of probability calibration with random support theory: Diagnosing case-based judgment’. Organizational Behavior and Human Decision Processes, 97(1):64–81.
Brenner, Lyle A, Griffin, Dale W, and Koehler, Derek J, 2012. ‘A Case-Based Model of Probability and Pricing Judgments : Biases in Buying and Selling Uncertainty’. Management Sciencee, 58(1):159–178.
Briggs, R., 2009a. ‘Distorted Reflection’. Philosophical Review, 118(1):59–85.
Briggs, Ray, 2009b. ‘The Anatomy of the Big Bad Bug’. Nous, 43(3):428–449.
Budescu, David V, Wallsten, Thomas S, and Au, Wing Tung, 1997. ‘On the importance of random error in the study of probability judgment. Part II: Applying the stochastic judgment model to detect systematic trends’. Journal of Behavioral Decision Making, 10(3):173–188.
Carr, Jennifer Rose, 2020. ‘Imprecise Evidence without Imprecise Credences’. Philosophical Studies, 177(9):2735–2758.
Christensen, David, 2010a. ‘Higher-Order Evidence’. Philosophy and Phenomenological Research, 81(1):185–215.
Christensen, David, 2010b. ‘Rational Reflection’. Philosophical Perspectives, 24:121–140.
Christensen, David, 2016. ‘Disagreement, Drugs, etc.: From Accuracy to Akrasia’. Episteme, 13(4):397–422.
Comesaña, Juan, 2020. Being Rational and Being Right. Oxford University Press.
Crupi, Vincenzo, Fitelson, Branden, and Tentori, Katya, 2008. ‘Probability, confirmation, and the conjunction fallacy’. Thinking & Reasoning, 14(2):182–199.
Crupi, Vincenzo, Tentori, Katya, and Lombardi, Luigi, 2009. ‘Pseudodiagnosticity Revisited’. Psychological Review, 116(4):971–985.
Cushman, Fiery, 2020. ‘Rationalization is rational’. Behavioral and Brain Sciences, 43:1–69.
Dawid, A P, 1982. ‘The Well-Calibrated Bayesian’. Journal of the American Statistical Association, 77(379):605–610.
Dawid, A. P., 1983. ‘Calibration-Based Empirical Inquiry’. The Annals of Statistics, 13(4):1251–1273.
Doody, Ryan, 2020. ‘The Sunk Cost “Fallacy” Is Not a Fallacy’. Ergo, 6(40):1153–1190.
Dorst, Kevin, 2019. ‘Higher-Order Uncertainty’. In Mattias Skipper Rasmussen and Asbjørn Steglich-Petersen, eds., Higher-Order Evidence: New Essays, 35–61. Oxford University Press.
Dorst, Kevin, 2020a. ‘Evidence: A Guide for the Uncertain’. Philosophy and Phenomenological Research, 100(3):586–632.
Dorst, Kevin, 2020b. ‘Higher-Order Evidence’. In Maria Lasonen-Aarnio and Clayton Littlejohn, eds., The Routledge Handbook for the Philosophy of Evidence. Routledge.
Dorst, Kevin, 2022. ‘Rational Polarization’. The Philosophical Review, To appear.
Dorst, Kevin, Levinstein, Benjamin, Salow, Bernhard, Husic, Brooke E., and Fitelson, Branden, 2021. ‘Deference Done Better’. Philosophical Perspectives, 35(1):99–150.
Dorst, Kevin and Mandelkern, Matthew, 2022. ‘Good Guesses’. Philosophy and Phenomenological Research, 105(3):581–618.
Dunn, Jeff, 2015. ‘Reliability for degrees of belief’. Philosophical Studies, 172(7):1929–1952.
Dunning, David, 2012. Self-Insight: Roadblocks and Detours on the Path to Knowing Thyself. Psychology Press.
Dunning, David, Griffin, Dale W., Milojkovic, James D, and Ross, Lee, 1990. ‘The Over-confidence Effect in Social Prediction’. Journal of Personality and Social Psychology, 58(4):568–581.
Ehrlinger, Joyce, Mitchum, Ainsley L., and Dweck, Carol S., 2016. ‘Understanding overconfidence: Theories of intelligence, preferential attention, and distorted self-assessment’. Journal of Experimental Social Psychology, 63:94–100.
Elga, Adam, 2013. ‘The puzzle of the unmarked clock and the new rational reflection principle’. Philosophical Studies, 164(1):127–139.
Elga, Adam, 2016. ‘Bayesian Humility’. Philosophy of Science, 83(3):305–323.
Erev, Ido, Wallsten, Thomas S, and Budescu, David V, 1994. ‘Simultaneous over-and underconfidence: The role of error in judgment processes.’ Psychological review, 101(3):519.
Fine, Cordelia, 2005. A Mind of Its Own: How Your Brain Distorts and Deceives. W. W. Norton & Company.
Fitelson, Branden and Hawthorne, James, 2010. ‘The Wason Task(s) and the Paradox of Confirmation’. Philosophical Perspectives, 24:207–241.
Gallow, J. Dmitri, 2021. ‘Updating for Externalists’. Noûs, 55(3):487–516.
Gibbons, John, 2013. The Norm of Belief. Oxford University Press.
Gigerenzer, Gerd, 1991. ‘How to make cognitive illusions disappear: Beyond “heuristics and biases”’. European review of social psychology, 2(1):83–115.
Gigerenzer, Gerd, Hoffrage, Ulrich, and Kleinbölting, Heinz, 1991. ‘Probabilistic mental models: a Brunswikian theory of confidence.’ Psychological review, 98(4):506.
Glaser, Markus and Weber, Martin, 2007. ‘Overconfidence and trading volume’. The Geneva Risk and Insurance Review, 32(1):1–36.
Glaser, Markus and Weber, Martin, 2010. ‘Overconfidence’. Behavioral finance: Investors, corporations, and markets, 241–258.
Greco, Daniel and Hedden, Brian, 2016. ‘Uniqueness and metaepistemology’. The Journal of Philosophy, 113(8):365–395.
Griffin, Dale and Tversky, Amos, 1992. ‘The Weighing of Evidence and the Determinants of Confidence’. Cognitive Psychology, 24:411–435.
Griffiths, Thomas L., Chater, Nick, Norris, Dennis, and Pouget, Alexandre, 2012. ‘How the Bayesians Got Their Beliefs (and What Those Beliefs Actually Are): Comment on Bowers and Davis (2012)’. Psychological Bulletin, 138(3):415–422.
Hahn, Ulrike and Harris, Adam J.L., 2014. ‘What Does It Mean to be Biased.: Motivated Reasoning and Rationality.’ In Psychology of Learning and Motivation -Advances in Research and Theory, volume 61, 41–102. Academic Press.
Hahn, Ulrike and Oaksford, Mike, 2007. ‘The rationality of informal argumentation: a Bayesian approach to reasoning fallacies.’ Psychological Review, 114(3):704–732.
Hall, Ned, 1994. ‘Correcting the Guide to Objective Chance’. Mind, 103(412):505–517.
Harris, Adam J L and Hahn, Ulrike, 2011. ‘Unrealistic optimism about future life events: A cautionary note.’ Psychological review, 118(1):135.
Hastie, Reid and Dawes, Robyn M, 2009. Rational Choice in an Uncertain World: The Psychology of Judgment and Decision Making. Sage Publications.
Hedden, Brian, 2019. ‘Hindsight Bias is Not a Bias’. Analysis, 79(1):43–52.
Hoffrage, Ulrich, 2004. ‘Overconfidence’. In Cognitive Illusions: A Handbook on Fallacies and Biases in Thinking, Judgement and Memory, 235–254. Psychology Press.
Holguín, Ben, 2022. ‘Thinking, Guessing, and Believing’. Philosophers’ Imprint, 22(1):1–34.
Horowitz, Sophie, 2014a. ‘Epistemic Akrasia’. Noûs, 48(4):718–744.
Horowitz, Sophie, 2014b. ‘Immoderately rational’. Philosophical Studies, 167:41–56.
Horowitz, Sophie, 2017. ‘Accuracy and Educated Guesses’. In Oxford Studies in Epistemology. Oxford University Press.
Horowitz, Sophie, 2019. ‘The Truth Problem for Permissivism’. The Journal of Philosophy, cxvi(5):237–262.
Howard, Michael, 1984. The Causes of Wars and Other Essays. Harvard University Press.
Icard, Thomas, 2018. ‘Bayes, Bounds, and Rational Analysis’. Philosophy of Science, 85(1):79–101.
Isaacs, Yoaav, 2021. ‘The Fallacy of Calibrationism’. Philosophy and Phenomenological Research, 102(2):247–260.
Jansen, Rachel, Rafferty, Anna N, and Griffiths, Tom, 2018. ‘Modeling the Dunning-Kruger Effect: A Rational Account of Inaccurate Self-Assessment.’ In CogSci.
Jansen, Rachel A., Rafferty, Anna N., and Griffiths, Thomas L., 2021. ‘A Rational Model of the Dunning–Kruger Effect Supports Insensitivity to Evidence in Low Performers’. Nature Human Behaviour, 5(6):756–763.
Johnson, Dominic D P, 2009. Overconfidence and War. Harvard University Press.
Johnson, Dominic D.P. and Fowler, James H., 2011. ‘The evolution of overconfidence’. Nature, 477(7364):317–320.
Joyce, James M, 1998. ‘A Nonpragmatic Vindication of Probabilism’. Philosophy of Science, 65(4):575–603.
Juslin, Peter, 1994. ‘The overconfidence phenomenon as a consequence of informal experimenter-guided selection of almanac items’. Organizational Behavior and Human Decision Processes, 57(2):226–246.
Juslin, Peter, Olsson, Henrik, and Björkman, Mats, 1997. ‘Brunswikian and thurstonian origins of bias in probability assessment: On the interpretation of stochastic components of judgment’. Journal of Behavioral Decision Making, 10(3):189–209.
Juslin, Peter, Wennerholm, Pia, and Olsson, Henrik, 1999. ‘Format Dependence in Subjective Probability Calibration’. Journal of Experimental Psychology: Learning Memory and Cognition, 25(4):1038–1052.
Juslin, Peter, Winman, Anders, and Olsson, Henrik, 2000. ‘Naive empiricism and dogmatism in confidence research: A critical examination of the hard–easy effect.’ Psychological review, 107(2):384.
Kahneman, Daniel, 2011. Thinking Fast and Slow. Farrar, Straus, and Giroux.
Kahneman, Daniel, Slovic, Paul, and Tversky, Amos, eds., 1982. Judgment Under Uncertainty: Heuristics and Biases. Cambridge University Press.
Kahneman, Daniel and Tversky, Amos, 1996. ‘On the reality of cognitive illusions.’ Psychological Review, 103(3):582–591.
Karlan, Brett, 2021. ‘Reasoning with heuristics’. Ratio, 34(2):100–108.
Kelly, Thomas, 2004. ‘Sunk costs, rationality, and acting for the sake of the past’. Nous, 38(1):60–85.
Kelly, Thomas, 2008. ‘Disagreement, Dogmatism, and Belief Polarization’. The Journal of Philosophy, 105(10):611–633.
Keren, Gideon, 1987. ‘Facing uncertainty in the game of bridge: A calibration study’. Organizational Behavior and Human Decision Processes, 39(1):98–114.
Kinney, David and Bright, Liam Kofi, 2021. ‘Risk aversion and elite-group ignorance’. Philosophy and Phenomenological Research, 1–23.
Koehler, Derek J, Brenner, Lyle, and Griffin, Dale, 2002. ‘The calibration of expert judgment: Heuristics and biases beyond the laboratory’. Heuristics and Biases: The Psychology of Intuitive Judgment, 686–715.
Koralus, Philipp and Mascarenhas, Salvador, 2013. ‘The erotetic theory of reasoning: bridges between formal semantics and the psychology of deductive inference’. Philosophical Perspectives, 27:312–365.
Kruger, Justin and Dunning, David, 1999. ‘Unskilled and Unaware of it: How Difficulties in Recognizing One’s Own Incompetence Lead to Inflated Self-Assessments’. Journal of Personality and Social Psychology, 77(6):121–1134.
Lam, Barry, 2011. ‘On the rationality of belief-invariance in light of peer disagreement’. Philosophical Review, 120(2):207–245.
Lam, Barry, 2013. ‘Calibrated probabilities and the epistemology of disagreement’. Synthese, 190(6):1079–1098.
Lasonen-Aarnio, Maria, 2013. ‘Disagreement and Evidential Attenuation’. Nous, 47(4):767–794.
Lasonen-Aarnio, Maria, 2015. ‘New Rational Reflection and Internalism about Rationality’. In Tamar Szabó Gendler and John Hawthorne, eds., Oxford Studies in Epistemology, volume 5, 145–171. Oxford University Press.
Lasonen-Aarnio, Maria, 2019. ‘Higher-Order Defeat and Evincibility’. Higher-Order Evidence: New Essays, 144–171.
Levi, Isaac, 1967. Gambling with Truth. The MIT Press.
Lewis, David, 1980. ‘A subjectivist’s guide to objective chance’. In Richard C Jeffrey, ed., Studies in Inductive Logic and Probability, volume 2, 263–293. University of California Press.
Lewis, David, 1994. ‘Humean Supervenience Debugged’. Mind, 103(412):473–490.
Lewis, Michael, 2016. The Undoing Project: A Friendship that Changed the World. Penguin UK.
Lichtenstein, Sarah, Fischhoff, Baruch, and Phillips, Lawrence D., 1982. ‘Calibration of probabilities: The state of the art to 1980’. In Daniel Kahneman, Paul Slovic, and Amos Tversky, eds., Judgment under Uncertainty, 306–334. Cambridge University Press.
Littlejohn, Clayton, 2012. Justification and the Truth-Connection. Cambridge University Press.
Littlejohn, Clayton, 2018. ‘Stop making sense? On a puzzle about rationality’. Philosophy and Phenomenological Research, 96(2):257–272.
Lord, Errol, 2018. The Importance of Being Rational. Oxford University Press.
Magnus, Jan R. and Peresetsky, Anatoly A., 2018. ‘Grade expectations: Rationality and overconfidence’. Frontiers in Psychology, 8(JAN):1–10.
Mahtani, Anna, 2017. ‘Deference, respect and intensionality’. Philosophical Studies, 174(1):163–183.
Mandelbaum, Eric, 2018. ‘Troubles with Bayesianism: An introduction to the psychological immune system’. Mind & Language, 1–17.
Merkle, Christoph and Weber, Martin, 2011. ‘True overconfidence: The inability of rational information processing to account for apparent overconfidence’. Organizational Behavior and Human Decision Processes, 116(2):262–271.
Moore, Don A, 2007. ‘When good = better than average’. Judgment and Decision Making, 2(5):277–291.
Moore, Don A, Carter, Ashli B, and Yang, Heather H J, 2015a. ‘Wide of the Mark: Evidence on the Underlying Causes of Overprecision in Judgment’. Organizational Behavior and Human Decision Processes, 131:110–120.
Moore, Don A and Healy, Paul J, 2008. ‘The Trouble with Overconfidence.’ Psychological Review, 115(2):502.
Moore, Don A, Tenney, Elizabeth R, and Haran, Uriel, 2015b. ‘Overprecision in judgment’. The Wiley Blackwell Handbook of Judgment and Decision Making, 2:182–209.
Myers, David G., 2010. Psychology. Worth Publishers, ninth edit edition.
Nebel, Jacob M., 2015. ‘Status quo bias, rationality, and conservatism about value’. Ethics, 125(2):449–476.
Oaksford, Mike and Chater, Nick, 1994. ‘A Rational Analysis of the Selection Task as Optimal Data Selection’. Psychological Review, 101(4):608–631.
Oaksford, Mike and Chater, Nick, 2007. Bayesian Rationality: The Probabilistic Approach to Human Reasoning. Oxford University Press.
O’Connor, Cailin and Weatherall, James Owen, 2018. ‘Scientific Polarization’. European Journal for Philosophy of Science, 8(3):855–875.
Odean, Terrance, 1999. ‘Do Investors Trade Too Much?’ American Economic Review, 89(5):1279–1298.
O’Hagan, Anthony, Buck, Caitlin E, Daneshkhah, Alireza, Eiser, J Richard, Garthwaite, Paul H, Jenkinson, David J, Oakley, Jeremy E, and Rakow, Tim, 2006. Uncertain judgements: eliciting experts’ probabilities. John Wiley & Sons.
Ortoleva, Pietro and Snowberg, Erik, 2015. ‘Overconfidence in political behavior’. American Economic Review, 105(2):504–535.
Pettigrew, Richard, 2016. Accuracy and the Laws of Credence. Oxford University Press.
Pettigrew, Richard and Titelbaum, Michael G, 2014. ‘Deference Done Right’. Philosopher’s Imprint, 14(35):1–19.
Pfeifer, Phillip E, 1994. ‘Are We Overconfident in the Belief that Probability Forecasters Are Overconfident?’ Organizational Behavior and Human Decision Processes, 58(2):203–213.
Plous, Scott, 1993. The Psychology of Judgment and Decision Making. Mcgraw-Hill Book Company.
Quilty-Dunn, Jake, 2020. ‘Unconscious Rationalization, or: How (Not) To Think About Awfulness and Death’.
Rinard, Susanna, 2019. ‘Believing for practical reasons’. Noûs, 53(4):763–784.
Roush, Sherrilyn, 2009. ‘Second Guessing: A Self-Help Manual’. Episteme, 251–268.
Roush, Sherrilyn, 2016. ‘Knowledge of Our Own Beliefs’. Philosophy and Phenomenological Research, 93(3):45–69.
Roush, Sherrilyn, 2017. ‘Epistemic Self-Doubt’.
Salow, Bernhard, 2018. ‘The Externalist’s Guide to Fishing for Compliments’. Mind, 127(507):691–728.
Schervish, M. J., Seidenfeld, T., and Kadane, J.B., 2004. ‘Stopping to Reflect’. The Journal of Philosophy, 101(6):315–322.
Schoenfield, Miriam, 2012. ‘Chilling out on epistemic rationality’. Philosophical Studies, 158(2):197–219.
Schoenfield, Miriam, 2014. ‘Permission to Believe: Why Permissivism is True and What it Tells Us About Irrelevant Influences on Belief’. Noûs, 48(2):193–218.
Schoenfield, Miriam, 2015. ‘A Dilemma for Calibrationism’. Philosophy and Phenomenological Research, 91(2):425–455.
Schoenfield, Miriam, 2016. ‘Bridging Rationality and Accuracy’. Journal of Philosophy, 112(12):633–657
Schoenfield, Miriam, 2018. ‘An Accuracy Based Approach to Higher Order Evidence’. Philosophy and Phenomenological Research, 96(3):690–715.
Schoenfield, Miriam, 2019. ‘Permissivism and the Value of Rationality: A Challenge to the Uniqueness Thesis’. Philosophy and Phenomenological Research, 99(2):286–297.
Schultheis, Ginger, 2018. ‘Living on the Edge: Against Epistemic Permissivism’. Mind, 127(507):863–879.
Seidenfeld, Teddy, 1985. ‘Calibration, Coherence, and Scoring Rules’. Philosophy of Science, 52:274–294.
Shariatmadari, David, 2015. ‘Daniel Kahneman: ‘What would I eliminate if I had a magic wand? Overconfidence’’. The Guardian.
Singer, Daniel J, Bramson, Aaron, Grim, Patrick, Holman, Bennett, Jung, Jiin, Kovaka, Karen, Ranginani, Anika, and Berger, William J, 2019. ‘Rational social and political polarization’. Philosophical Studies, 176(9):2243–2267.
Sliwa, Paulina and Horowitz, Sophie, 2015. ‘Respecting All the Evidence’. Philosophical Studies, 172(11):2835–2858.
Staffel, Julia, 2020. Unsettled Thoughts: A Theory of Degrees of Rationality. Oxford University Press, USA.
Tenenbaum, Joshua B and Griffiths, Thomas L, 2006. ‘Optimal Predictions in Everyday Cognition’. Psychological Science, 17(9):767–773.
Tenenbaum, Joshua B, Kemp, Charles, Griffiths, Thomas L, and Goodman, Noah D, 2011. ‘How to Grow a Mind: Statistics, structure, and Abstraction’. Science, 331(6022):1279–1285.
Tetlock, Philip E and Gardner, Dan, 2016. Superforecasting: The Art and Science of Prediction. Random House.
Thaler, Richard H., 2015. Misbehaving: The Making of Behavioural Economics. Penguin.
Thorstad, David, 2021. ‘The accuracy-coherence tradeoff in cognition’. British Journal for the Philosophy of Science, To appear.
Tversky, Amos and Kahneman, Daniel, 1974. ‘Judgment under uncertainty: Heuristics and biases’. Science, 185(4157):1124–1131.
Tversky, Amos and Kahneman, Daniel, 1983. ‘Extensional Versus Intuitive Reasoning: The Conjunction Fallacy in Probability Judgment.’ Psychological Review, 90(4):293.
Vallone, Robert P., Griffin, Dale W., Lin, Sabrina, and Ross, Lee, 1990. ‘Overconfident Prediction of Future Actions and Outcomes by Self and Others’. Journal of Personality and Social Psychology, 58(4):582–592.
van Fraassen, Bas, 1983. ‘Calibration: A Frequency Justification for Personal Probability’. In R.S. Cohen and L Laudan, eds., Physics, Philosophy, and Psychoanalysis: Essays in Honor of Adolf Gr unbaum, 295–318. D. Reidel Publishing Company.
van Fraassen, Bas, 1984. ‘Belief and the Will’. The Journal of Philosophy, 81(5):235–256.
van Prooijen, Jan-Willem and Krouwel, André P M, 2019. ‘Psychological Features of Extreme Political Ideologies’. Current Directions in Psychological Science, 28(2):159–163.
Wallsten, Thomas S., Budescu, David V., and Zwick, Rami, 1993. ‘Comparing the Calibration and Coherence of Numerical and Verbal Probability Judgments’. Management Science, 39(2):176–190.
Wedgwood, Ralph, 2017. The Value of Rationality. Oxford University Press.
White, Roger, 2005. ‘Epistemic Permissiveness’. Philosophical Perspectives, 19(1):445–459.
White, Roger, 2009a. ‘Evidential Symmetry and Mushy Credence’. In Tamar Szabó Gendler and John Hawthorne, eds., Oxford Studies in Epistemology, volume 3, 161–186. Oxford University Press.
White, Roger, 2009b. ‘On Treating Oneself and Others as Thermometers’. Episteme, 6(3):233–250.
Williamson, Timothy, 2000. Knowledge and its Limits. Oxford University Press.
Williamson, Timothy, 2019. ‘Evidence of Evidence in Epistemic Logic’. In Mattias Skipper and Asbjørn Steglich-Petersen, eds., Higher-Order Evidence: New Essays, 265–297. Oxford University Press.