We deliberate about things that are in our power and can be done.
Aristotle, Nicomachean Ethics III, 3, 7
1. Introduction
In the Nicomachean Ethics, Aristotle describes deliberation as an exercise in thinking about the means to achieve certain ends when ends can be brought about by our own efforts. The means-ends aspect has been explored exhaustively in modern approaches to rational choice, starting with Pascal and, in particular, the Port Royal Logic in the 17th century and leading all the way up to Ramsey, Savdescendantsage and their intellectual descendants.1 Deliberation—understood as a dynamic process of thinking things through—has played only a minor role in these developments. Rational choice is conceived of as static in that a rational agent maximizes expected utility with respect to her current beliefs and desires. On this picture, the only door through which deliberation enters, besides the straightforward calculation of expected utilities, is in setting up a decision problem. This, however, is not itself a part of the theory, but something that happens before the theory is applied.
Deliberation is sometimes taken more seriously, notably in one strand of the debate between causal and evidential decision theory. Evidential decision theory, as developed in Richard Jeffrey’s Logic of Decision,2 holds that rational choice consists in maximizing a kind of expected utility that takes into account the evidence acts provide about states of the world. This is adequate whenever acts can change states of the world; but the evidential paradigm is not compelling when acts are merely correlated with, but have no causal influence on, states. This has given rise to various forms of causal decision theory, which are all based on the principle of maximizing expected utility with respect to probabilities that capture one’s beliefs about the causal structure of the world.3 The two decision theories are incompatible whenever causal and evidential beliefs come apart (see §2).
The debate between causal and evidential decision theory is ongoing, with several contemporary philosophers leaning toward evidentialism.4 However, some evidentialists have tried to bring evidential decision theory closer to causal intuitions in Newcomb style problems. In particular, Richard Jeffrey and Ellery Eells have argued that evidential decision theory has the means to speak to causal concerns within the context of deliberation.5 Their argument is known as the “tickle” or the “metatickle” defense. Much of the criticism that has been directed against the metatickle argument takes issue with its basic assumptions.6 But the argument faces a more fundamental roadblock. Even if we grant Eells’ and Jeffrey’s assumptions, Brian Skyrms has shown that their view of deliberation does not lead to a robust reconciliation between evidential and causal decision theory.7
I’m going to lay out Skyrms’ argument in §3 and §4. My main goal is to develop an alternative to Skyrms’ account of deliberative decision theory. By departing from one key assumption made by Skyrms, Eells, and Jeffrey, I show that there exist plausible models that remove Skyrms’ roadblock. After explaining these models in §5, I discuss their scope in §6. My proposal is modest: while there is broader agreement between the theories than previously thought, the reconciliation between causal and evidential decision theory is not universal. Cases of conflict, however, only arise when a decision maker expects not to be fully effective as an agent.
2. Two Paradigms of Decision Making
In what is considered standard decision theory in economics and adjacent fields, a sharp distinction is drawn between states of the world and acts.8 States are outside a decision maker’s control. They are the objects of an agent’s uncertainty, expressed by probability assignments. Acts map states to more or less desirable consequences. The agent has preferences over acts, but acts are not assigned probabilities.
Causal and evidential decision theory both depart from this framework.9 Jeffrey’s evidential decision theory takes states of the world and acts (together with consequences) to be propositions closed under Boolean operations.10 Probabilities can thus be assigned not just to states, but also to acts and to states conditional on acts.11 Acts may, therefore, have evidential bearing on states.
Causal decision theory, which I shall take to be structured along the lines of Lewis’ approach, goes along with this: acts can provide evidence about states. Otherwise, Lewis stays quite close to Savage’s decision theory. He takes states of the world to be dependency hypotheses—i.e., propositions that capture all relevant causal relationships. They are, in virtue of this, causally independent of acts, reflecting Savage’s requirement that the decision maker exerts no control over states of the world.12
In terms of the epistemic setup, then, evidential and causal decision theory agree. They part ways in how they evaluate the choiceworthiness of acts. Causal decision theory considers the causal efficacy of choices to be crucial. Evidential decision theory evaluates acts in light of the evidence they provide about states.
To illustrate, let’s consider decision situations with two states and two acts. Decision problems of this kind can be given, as in Table 1, by a two-by-two table. Consequences are expressed as conjunctions of states, S1 and S2, and acts, A1 and A2. Let DES(S & A) denote the desirability (utility) of the outcome that results from choosing act A when the state of the world is S. Also, let PROB(S | A) be the probability of S conditional on choosing A and PROB(S) the unconditional probability of S.
A two-act, two-state decision problem.
| S1 | S2 | |
|---|---|---|
| A1 | DES(A1&S1) | DES(A1&S2) |
| A2 | DES(A2&S1) | DES(A2&S2) |
Evidential decision theory recommends choosing an act, A, that maximizes the following expected value, denoted V:
Expected desirability is taken with respect to conditional probabilities of states given acts.Causal decision theory recommends choosing A if it maximizes the following causal expected utility:
This expectation is calculated relative to unconditional probabilities of states. Since states are dependency hypotheses, they capture all causal links between states and acts. As a result, unconditional probabilities of states already capture the causal efficacy of acts to obtain desirable outcomes, and so the probabilities of acts don’t figure into calculating causal expected utility.Causal and evidential decision theory go hand in hand as long as evidence for good outcomes tracks causal relationships; otherwise they come apart. Newcomb’s problem is the best-known case of conflict. The basic setup has one opaque and one transparent box. The transparent box contains a thousand dollars. The opaque box contains either a million dollars or nothing. You must decide between choosing only the transparent box, A1, or both boxes, A2. The payoffs are shown in Table 2.13
Newcomb’s problem.
| Box empty | Box not empty | |
|---|---|---|
| A1 | $0 | $1,000,000 |
| A2 | $1,000 | $1,001,000 |
So far there is no conflict between evidential and causal decision theory. The opaque box is either empty or not; no causal or evidential link between acts and states has been stipulated. Both causal and evidential decision theory recommend choosing A2 (choosing one box is worse by a thousand dollars no matter what).
Introducing evidential links with no causal underpinnings drives a wedge between the two theories. The usual story runs like this: An eccentric person with a million dollars to spare places the money in the opaque box before you make a decision if he predicts that you are going to choose only the opaque box; otherwise, he leaves the box empty. The catch is that, besides being wealthy and eccentric, you believe that he is also is a very good predictor. This makes your choice evidentially relevant for whether or not the million is under the opaque box. Your conditional probability that the million is in the box given that you choose just one box is high, while the probability that the million is in the box given that you choose both boxes is low. Suppose, for instance, that PROB(box not empty | choose one box) = 9/10 and PROB(box not empty | choose both boxes) = 1/10 (nothing much depends on particular values). Then
and Since V(A1) is larger than V(A2), evidential decision theory recommends choosing one box.Causal decision theory does not deny the evidential link between acts and states: one-boxing does provide evidence that the million is in the box. But since the million is either there or not, there is no causally relevant difference between the earlier setting with no predictor and the present one. Causal decision theory thus recommends choosing both boxes.
3. Metatickles
At this point, proponents of evidential decision theory find themselves at a crossroads. They can either defend one-boxing in Newcomb’s problem (and similarly problematic acts in other decision situations), or they can try to include causal considerations into evidential decision theory without radically altering its core ideas. Eells, Jeffrey, and Skyrms explored the latter approach. Skyrms developed the most promising methodology. To set the stage, though, I’m going to consider Eells’ original argument, which gave rise to the project of trying to include causal considerations into evidential decision theory.
A “tickle” is a reliable signal of underlying states. Suppose, for example, that you feel a tickle in your left pinkie in case the predictor has put the million in the box, and that the tickle is absent otherwise. Then, even though the presence of the million depends probabilistically on your act, the tickle is sufficient and screens off states from acts: the probability of the million being in the box (or not) conditional on the tickle and the act you contemplate choosing is the same as the probability of the million being in the box (or not) given just the tickle. The act provides no additional information.
In the presence of a tickle, then, states are evidentially independent of acts. As a result, evidential decision theory agrees with causal decision theory in Newcomb’s problem. But are tickles always available? Eells argued that a special type of tickle, called a “metatickle”, is always at hand for sophisticated decision makers. A metatickle is a proposition about the agent’s beliefs and desires.14 Metatickles enter Newcomb problems as follows. It is reasonable to assume the existence of a common cause that influences both states and acts. The thought is that there has to be something—in the agent’s cognitive system or decision making faculty—that allows the predictor to forecast choices. Based on this, Eells suggests the following (where “symptomatic act” refers to acts that indicate the presence of a common cause):
In other words, Eells thinks that regardless of how exactly the hypothesized common cause influences the agent’s choices, the influence has to go through her probabilities and desirabilities, assuming she is rational. Now, states and acts are independent conditional on the common cause once the decision maker gains knowledge about her probabilities and desirabilities (i.e. the metatickle); and since knowledge of her metatickle provides full information about the common cause, states and acts are independent given the metatickle. For a rational deliberator, evidential expected utility conditional on the metatickle is equal to causal expected utility.I shall assume that the way in which a common cause causes a rational person to perform a symptomatic act is by causing him to have such beliefs and desires that a rational evaluation of the available acts in light of these beliefs and desires leads to the conclusion that the symptomatic act is the best act. And I shall assume that our agent believes this hypothesis about how the common cause causes the symptomatic act.15.
Here, rational deliberation comes in by way of the decision maker realizing what her probabilities and desirabilities are. The decision maker does not just blindly act as prompted by her attitudes. She instead goes through a process of reflection during which she realizes what those attitudes are and endorses them as rational.
Introducing common causes is a plausible vignette for thinking about Newcomb-like situations. But I think it can be dropped without damaging the core idea of the metatickle argument. In his version of the metatickle approach, Jeffrey stated that
When applying this idea to Newcomb’s problem, Jeffrey’s thought is that at the beginning of deliberation acts do give evidence about states; at the end of deliberation, however, the agent’s choice is based solely on her final probabilities and desirabilities (as well as her decision theory), and acts provide no information beyond this metatickle. Metatickles can be thought of as a kind of sufficient statistic with regard to the evidence acts provide about states. If this is correct, causal and evidential decision theory are again in agreement.it is my credences and desirabilities at the end of deliberation that correspond to the preferences in the light of which I act, i.e., it is my final credence and desirability functions […] not the initial ones […] that underlie my choice.16
There is something intuitively appealing about this idea, though several commentators have pointed out gaps, implicit assumptions, and idealizations that may limit the reach of the metatickle approach.17 In my view, the most glaring gap is Eells’ and Jeffrey’s somewhat cavalier treatment of deliberation. In Eells’ basic argument it’s not clear where the probabilities and desirabilities that constitute the metatickle come from.18 Are they the agent’s initial attitudes? Do they arise during deliberation? If so, how are they acquired? Jeffrey, as we have seen, thought that decisions are made based on final probabilities and desirabilities. Are there any restrictions on final probabilities and desirabilities? How are they related to the initial ones? What are the principles that guide deliberation? A full appraisal of the metatickle argument is out of reach as long as these questions remain unanswered.
In contrast to learning from observations, which relies on external inputs, deliberation is pure thinking about a decision problem. Why would one engage in such an activity? The Aristotelian answer is that it helps in making decisions. Deliberation often leads to a more informed state of mind. How does it result in more information? Suppose acts and states are correlated (as in Newcomb’s problem). Then there is, as Skyrms pointed out, an evidential feedback loop that goes from acts via states and expected utilities back to acts.19 To make things more precise, let the decision maker’s initial uncertainty as to which act she will choose be given by choice probabilities. The probability assigned to an act represents the agent’s credence that she will choose that act at the end of deliberation. Since states and acts are correlated, choice probabilities provide evidence about states of the world; for instance, a high probability of one-boxing indicates that the million has probably been stashed in the box. Suppose the agent updates probabilities of states in response to the information given by choice probabilities, and suppose that the utility of outcomes is not affected by deliberation. Since expected utilities are functions of (conditional) state probabilities and utilities, any change in the former may lead to a change in how acts are evaluated. This, in turn, provides information about how the decision maker will choose (if she chooses in accordance with her decision theory—a plausible assumption when analyzing decision theories by augmenting them with deliberative considerations). In taking the last step, the feedback loop has returned to acts; the decision maker adjusts choice probabilities and, if there is more information to be had, runs through the loop again.
Joyce, following Skyrms’ approach to deliberation, has argued that rational choice theory hinges on a full information requirement: decisions ought to be made from a maximally informed state of mind—only then are they fully rational.20 From a bounded rationality point of view, this is a tall order: real-world deliberation always involves costs. However, taking deliberation to be an idealized process is appropriate for the present discussion. Our goal is to study best versions of causal and evidential decision theory, not to design new bounded rationality decision theories. Requiring an agent’s attitudes to be based on all available information is natural for the best-version setting.21
The metatickle idea fits smoothly into this approach. Deliberation is driven by correlations between acts and states, i.e., by the fact that the probability of states given acts, PROB(S | A), is not equal to the unconditional probability of states, PROB(S). As the decision maker deliberates, the evidence acts provide about states becomes incorporated into her evolving metatickle (her up-to-date probabilities and desirabilities). Thus, conditional on the metatickle, T, the correlation between states and acts should decrease. That is, PROB(S | A&T) and PROB(S | T) get closer. If, at the end of deliberation, T is sufficient, states become fully independent of acts conditional on T.
Does deliberation always uncover all the evidence acts give about states? Are there plausible reasons that it might not? I will return to these questions in §6. Following the footsteps of Eells and Jeffrey, the next two sections proceed under the assumption that metatickles eventually include all relevant information. In the next section we will see that, even under this charitable assumption, it looks like the metatickle approach does not work.
4. Rational Deliberation
Suppose the decision maker’s probability of choosing two boxes, PROB(A2), changes in response to deliberation. In what’s perhaps the simplest plausible model, the rate of change, dPROB(A2)/dt, is proportional to the difference in the expected utility of A2 and the expected utility of A1. Formally, taking expected utility in the evidentialist sense with respect to the agent’s current conditional probabilities:
I will refer to this as Skyrms’ law of motion.22 The law says that deliberation flows in the direction of the act that currently has higher expected desirability.23 A deliberator who follows Skyrms’ law of motion takes an act’s current expected desirability as her best estimate of its final expected desirability and adjusts her choice probabilities accordingly.The expected desirabilities V(A1) and V(A2) depend on the two conditional probabilities PROB(M | A1) and PROB(M | A2), where M denotes the proposition that the million is in the opaque box. Thus, a dy namics that follows Skyrms’ law of motion depends on how deliberation affects conditional probabilities. It is often assumed that deliberation leaves PROB(M | A1) and PROB(M | A2) untouched: the conditional probabilities are rigid and probabilities are revised by probability kinematics on the act partition.24 In this case, deliberation (almost) always leads to choosing one box: since PROB(M | A1) remains large and PROB(M | A2) remains small, V(A2) < V(A1) and PROB(A2) decreases.
Rigidity runs against the metatickle idea, however. That probabilities are revised by probability kinematics on the act partition means that the decision maker acquires information only about acts during deliberation. Eells’ metatickle argument has the agent learning also about her current credences and desirabilities, with the result that conditional probabilities, PROB(M | A1) and PROB(M | A2), are altered by deliberation in a way that reflects decreasing evidential dependence of states on acts: the more one learns about one’s attitudes, the closer the relevant conditional probabilities get. Skyrms translates this idea into the following assumption: the absolute difference between PROB(M | A1) and PROB(M | A2) is a continuous function of PROB(A2) that goes to zero as PROB(A) approaches one or zero.25 2 That the absolute difference between PROB(M | A1) and PROB(M | A2) goes to zero in this way can be understood in terms of states becoming conditionally independent of acts given metatickles, assuming that metatickles get fully informed as the decision maker becomes more certain what she’ll do. This assumption, which I shall discuss in more detail below, can be traced back to Jeffrey and Eells, who both think of the end of deliberation as a state in which the agent is (almost) certain what to do.26
Skyrms showed that, within this setting, deliberation does not always lead to two-boxing. The argument goes as follows. Deliberation tracks the evolution of PROB(A2). As PROB(A2) goes to zero or one, the absolute difference between PROB(M | A1) and PROB(M | A2) shrinks. Their absolute difference is maximal when the decision maker is in a state of indecision, for example if (nothing hinges on this value being equal to , it only needs to be strictly between zero and one). At states around , then, PROB(M | A1) is considerably larger than PROB(M | A2). This implies V(A2) < V(A1). Hence, by Skyrms’ law of motion, PROB(A2) decreases toward zero. However, as PROB(A2) decreases toward zero, the absolute difference between PROB(M | A1) and PROB(M | A2) also decreases toward zero continuously in PROB(A2). It follows that there exists a value, p, of PROB(A2) at which the absolute difference between PROB(A1) and PROB(A2) is exactly such that V(A1) = V(A2). At PROB(A2) = p the deliberative dynamics is in equilibrium. Values of PROB(A2) larger than p approach the equilibrium. For values of PROB(A2) less than p, the absolute difference between PROB(M | A1) and PROB(M | A2) is small enough so that V(A2) > V(A1). Hence, by Skyrms’ law of motion, if PROB(A2) < p the deliberative dynamics also approaches the equilibrium. The equilibrium at PROB(A2) = p is thus asymptotically stable. The dynamics close to the deliberative equilibrium is sketched in Figure 1.
Similar considerations show that there is another equilibrium close to PROB(A2) = 1 (also shown in Figure 1). This equilibrium is unstable. As PROB(A2) increases to one, there is a value, q, of PROB(A2) such that V(A1) = V(A2). For values of PROB(A2) less than q, V(A1) > V(A2), and so the dynamics goes toward the equilibrium PROB(A2) = p. For values PROB(A2) larger than q, V(A1) < V(A2). In that case, the deliberative dynamics converges to PROB(A2) = 1, which is another asymptotically stable equilibrium.
There are, hence, two stable equilibria. In one the decision maker is certain to choose two boxes. In the other she remains stuck in a state of indecision where she assigns positive probability to both A1 and A2. The endpoint of the dynamics depends on the initial value of PROB(A2).
Skyrms’ argument rests on the following assumptions:
(i) The deliberative system dPROB(A2)/dt satisfies Skyrms’ law of motion.
(ii) The absolute difference between PROB(M | A1) and PROB(M | A2) goes to zero continuously as PROB(A2) goes to zero or one.
As a result, the idea promoted by Eells and Jeffrey cannot easily be grounded in a dynamical model. Eells and Jeffrey took it for granted that at the end of deliberation knowledge of one’s attitudes makes states independent from acts and thus lets the evidential decision theorist choose two boxes. Skyrms demonstrated that, under plausible evidential principles, this need not happen. This suggests that the end of deliberation that Eells and Jeffrey had in mind is a chimera which cannot be reached from the bottom-up.
5. Generalized Rational Deliberation
It is clear that in order to avoid this conclusion, one of the two foregoing assumptions has to go. In his response to Skyrms, Eells devised an alternative model of deliberation that does away with (i) (Skyrms’ law of motion), while upholding (ii) (the absolute difference between PROB(M | A1) and PROB(M | A2) goes to zero as a continuous function of PROB(A2) as the latter goes to zero or to one).28 In addition, Eells’ model features an agent’s attitudes toward the urgency to act. Depending on how quickly one wants to reach a decision, one shuns states of indecision during later stages of deliberation. With this in hand, Eells argues that evidential deliberation leads to two-boxing in Newcomb’s problem.
This line of reasoning faces a general methodological hurdle. The idea underlying the original metatickle argument is to modify evidential decision theory in a minimal way so as to align it with causal decision theory. Eells’ model of deliberation goes significantly further. Whether a decision maker procrastinates or rushes into a choice are features of the agent that are not expressed through the underlying decision theory, i.e., in terms of her preferences. Instead, part of her preferential attitudes are being expressed by her deliberative thinking. As a result, Eells’ project is better described as developing a new decision theory—a deliberative decision theory that includes aspects of, but is not the same as, evidential decision theory. The Eellsian model, therefore, arguably fails to achieve a reconciliation between evidential and causal decision theory.29
Eells is right in pointing out that there is no room for reconciliation unless we abandon one of Skyrms’ assumptions. Skyrms’ law of motion is plausible whenever the agent takes her current expected desirabilities to be the best estimates of her final expected desirabilities—for it is in this case that she should become more confident that she will choose whichever act has higher current expected desirability at the end of deliberation. The second assumption—that the absolute difference of PROB(M | A1) and PROB(M | A2) goes to zero as PROB(A2) goes to zero or one—is more problematic. It is supposed to express the Eellsian idea that at the end of deliberation any correlation between states and acts has vanished. But it identifies the end of deliberation with being certain to choose a particular act. This is too restrictive: the end of deliberation might be a state of indecision. That such a state is reached at the end of deliberation is entirely consistent with states and acts being uncorrelated. In Skyrms’ model, however, a state of indecision may be reached at the end of deliberation with states and acts still being dependent. This suggests that Skyrms’ model is not fully faithful to the Eellsian idea of a metatickle.
What should replace Skyrms’ assumption (ii)? There is a way to generalize the assumption without presuming anything about the end of deliberation that is perfectly in line with the Eellsian idea of how deliberation affects conditional probabilities. I shall assume that the decision maker expects PROB(M | A1) and PROB(M | A2) to be equal at the end of deliberation whatever it may be. To make this explicit, I introduce them as two new variables into the dynamical system. In addition to PROB(A2), which keeps track of the agent’s belief that she will choose A2 at the end of deliberation, the dynamics also keeps track of the agent’s current probabilities conditional on acts: PROB(M | A1) and PROB(M | A2). Skyrms’ assumption (ii) is replaced with the requirement that PROB(M | A1) and PROB(M | A2) evolve toward what I call the “Eells-Jeffrey manifold”: the set of states at which PROB(M | A1) = PROB(M | A2). Here is one way to capture this idea qualitatively:
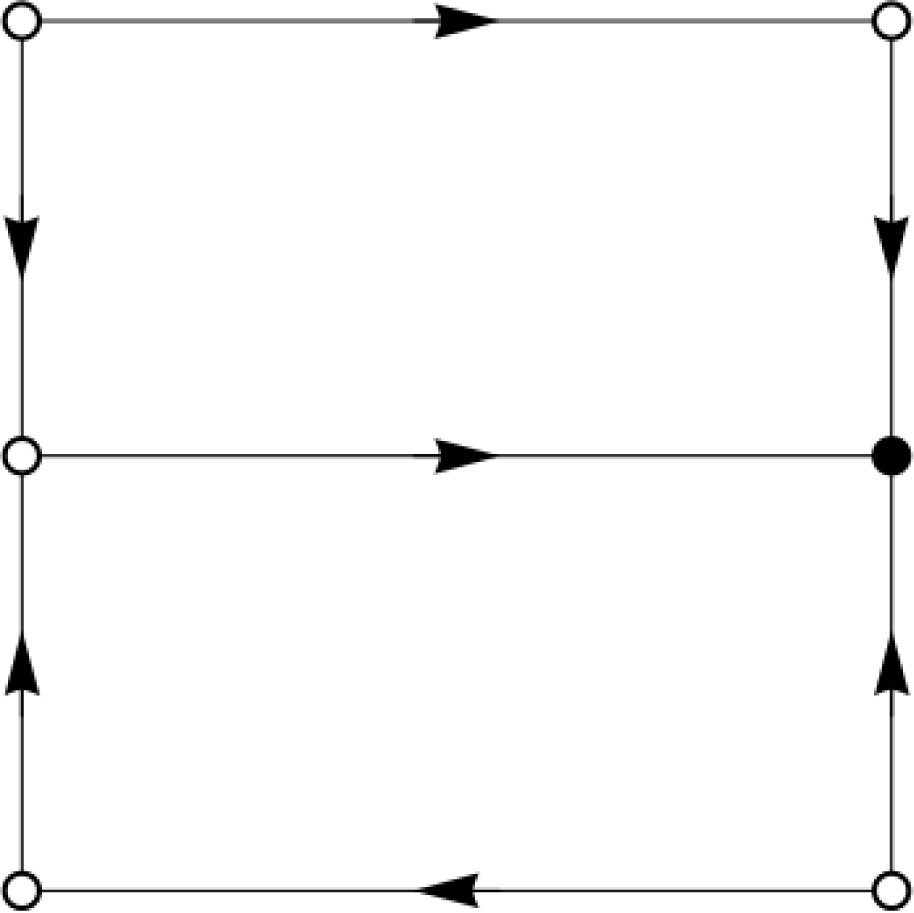
and I also take as part of the Eellsian package that correlations do not reappear: if PROB(M | A1) = PROB(M | A2). Thus, the Eells-Jeffrey manifold is invariant: once it’s reached, the dynamics does not leave the manifold. I will refer to the three foregoing conditions as the “independence dynamics”. The independence dynamics captures, at the level of probabilities, the Eellsian idea that during deliberation correlations between states and acts vanish because the decision maker learns about her own inclinations; and, once she has learned enough about her own inclinations, states remain independent of acts (given what she has learned).Let me first illustrate this idea with a simple case. Let’s assume that PROB(M | A1) = 1 − PROB(M | A2) (this is compatible with assuming that the predictor in Newcomb’s problem is reliable). Then the deliberative dynamics tracks the choice probability PROB(A2) and the conditional probability PROB(M | A2). Both variables take on values between zero and one. The resulting state space consists of all pairs of real numbers (x, y) between zero and one, where x is the value of PROB(A2) and y is the value of PROB(M | A2). States of the system can thus be identified with the unit square as shown in Figure 2. The horizontal axis represents all possible values of PROB(A2), and the vertical axis represents all possible values of PROB(M | A2).
A first step to analyze the dynamical system is to consider the dynamics on the boundary. In the present model, the boundary consists of the following four sets of states:
(i) PROB(M | A2) = 0 and PROB(A2) ranges from 0 to 1;
(ii) PROB(M | A2) = 1 and PROB(A2) ranges from 0 to 1;
(iii) PROB(A2) = 1 and PROB(M | A2) ranges from 0 to 1; and
(iv) PROB(A2) = 0 and PROB(M | A2) ranges from 0 to 1.
The set of states (i) is represented by the bottom edge of the square in Figure 2. Here, the act of choosing one box is perfectly correlated with the million being in the box: PROB(M | A2) = 0. Thus, Skyrms’ law of motion implies that dPROB(A2)/dt < 0, since V(A2) > V(A1) for all states in (i) with 0 < PROB(A2) < 1. Hence, the value of PROB(A2) decreases to zero under evidential deliberation. This is indicated in Figure 2 by an arrow that points to the left.
The set of states (ii) is represented by the top edge in Figure 2. The act of choosing one box is perfectly anti-correlated with the million being in the box: PROB(M | A2) = 1. Deliberation thus has the opposite effect from states of type (i). For all states in (ii) with 0 < P(A2) < 1, Skyrms’ law of motion entails dPROB(A2)/dt > 0. As a result, deliberation goes to PROB(A2) = 1.
The set of states given in (iii) and (iv) corresponds to the left and right edges of the square in Figure 2, respectively. Here, the dynamics is not governed by Skyrms’ law of motion since the probability of A2 is assumed to be fixed. The independence dynamics, though, implies that for all states in (iii) and (iv) with PROB(M | A2) < PROB(M | A1), the rate of change dPROB(M | A2)/dt is positive. For all states in (iii) and (iv) with PROB(M | A2) > PROB(M | A1), the rate of change dPROB(M | A2)/dt is negative. In both cases, the deliberative dynamics evolves toward PROB(M | A2 = PROB(M | A1) = 1/2. In Figure 2 this is represented by the arrows pointing upward and downward on the left and right edges. For the two states in (iii) and (iv) with PROB(M | A2) = 1/2, we stipulate that they are equilibria of the independence dynamics. Thus, on the two sets of states (iii) and (iv) deliberation evolves toward the midpoints.
Next, consider states with PROB(M | A1) = PROB(M | A2), which corresponds to the Eells-Jeffrey manifold in this simple model and is represented by the horizontal line in the middle of Figure 2. By the independence dynamics, this set of states is invariant, and by Skyrms’ law of motion deliberation flows toward higher values of PROB(A2): dPROB(A2)/dt > 0 since independence of M from the acts implies V(A2) > V(A1). In Figure 2 this is represented by an arrow pointing to the right on the horizontal line in the middle.
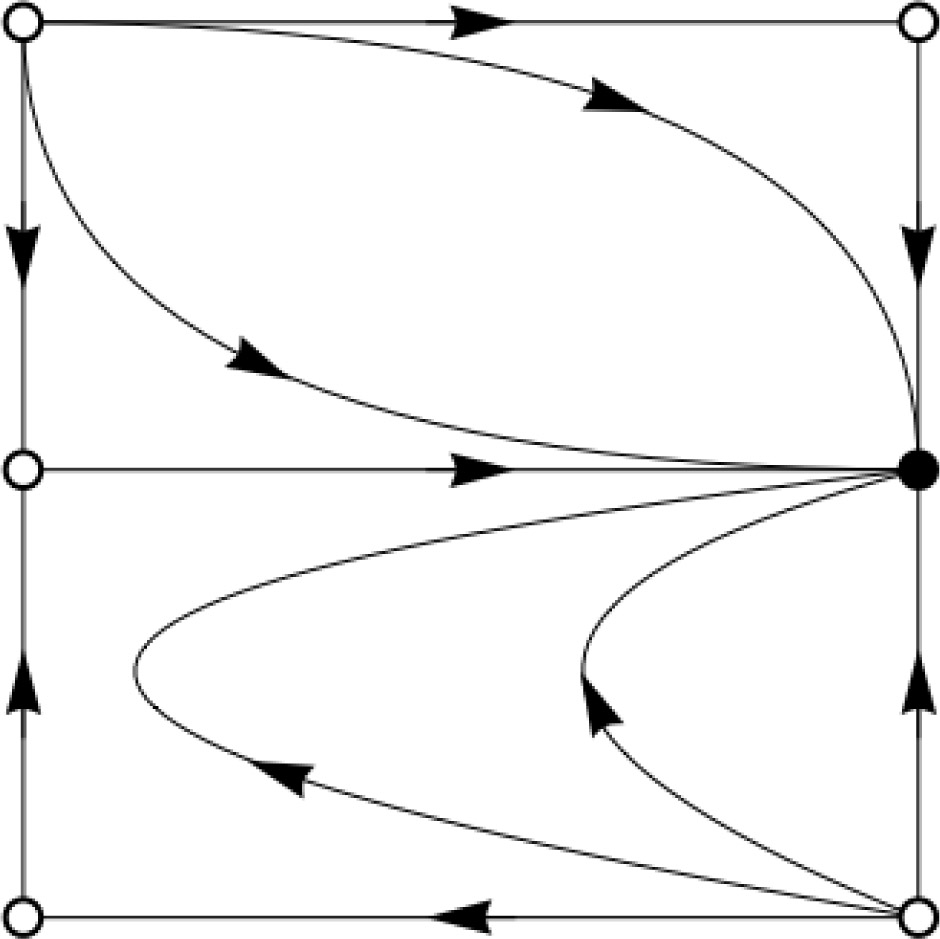
According to the foregoing qualitative analysis, no state on the boundary can be a stable equilibrium other than the state with PROB(A2) = 1 and . If we assume that the dynamics in the interior of the square obeys the same qualitative constraints as the dynamics on the boundary, that’s also true for the full state space. For all states with PROB(M | A2) > 1/2, dPROB(A2)/dt > 0 and dPROB(M | A2)/dt < 0. This implies that whenever the initial state is one where PROB(M | A2) > 1/2, the dynamics converges to the equilibrium PROB(A2) = 1 and . The dynamics is different for states with PROB(M | A2) < 1/2. For sufficiently small values of PROB(M | A2) the rate of change dPROB(A2)/dt is negative since V(A1) > V(A2). On the other hand, according to the independence dynamics, dPROB(M | A2)/dt is positive throughout the set of states with PROB(M | A2) < 1/2. Thus, as PROB(A2) decreases, PROB(M | A2) increases. Once PROB(M | A2) is sufficiently large, the difference between PROB(M | A2) and PROB(M | A1) is small enough so that V(A2) > V(A1). In fact, under standard continuity assumptions there exists a difference between PROB(M | A2) and PROB(M | A1) such that dPROB(A2)/dt = 0. For smaller differences, dPROB(A2)/dt > 0, and hence PROB(A2) increases. Overall, the dynamics again converges to the rest point PROB(A2) = 1 and . The trajectories are illustrated in Figure 3.
To recap, the qualitative constraints governing deliberational dynamics are (i) Skyrms’ law of motion and (ii) an independence dynamics. If deliberation is, in addition, smooth and constrained by PROB(M | A1) = 1 − PROB(M | A2), and if there are no other fac tors that influence the dynamics, then there is a unique asymptotically stable rest point at which the decision maker is certain that she will choose A2 and at which . This rest point attracts all initial states. It is a global attractor.30
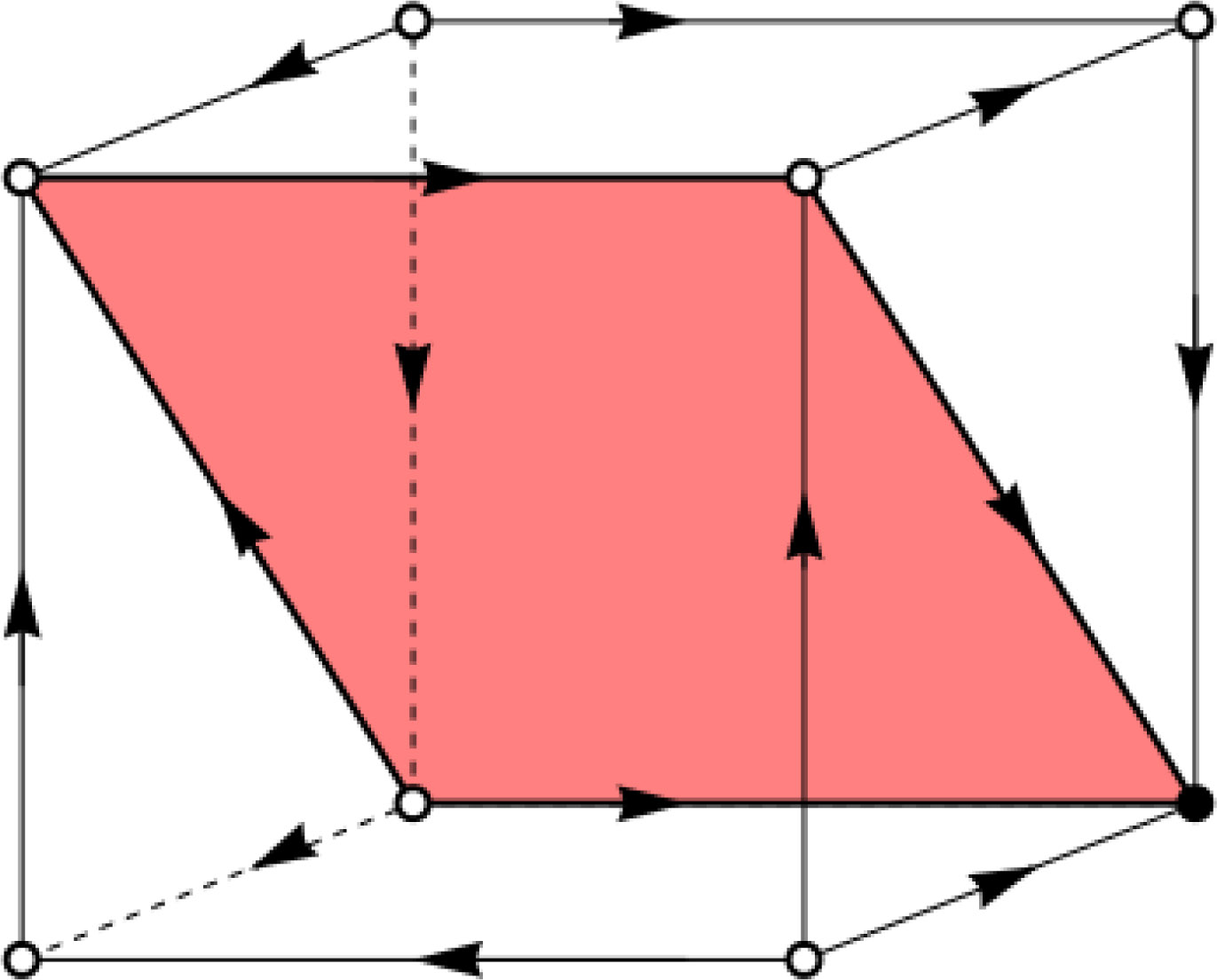
One aspect of the previous analysis—that in equilibrium —might be a cause for concern. Why should the decision maker at the end of deliberation have even odds on the million being in the box no matter what she chooses? This conclusion is an artifact of the assumption that PROB(M | A1) = 1 − PROB(M | A2). It can be removed by allowing both conditional probabilities to vary under deliberational dynamics. If PROB(M | A1) and PROB(M | A2) vary independently, the state space is the unit cube. In Figure 4 the horizontal axis represents PROB(A2), the vertical axis PROB(M | A2), and the third axis PROB(M | A1). In order to make the analysis of this model more accessible, we will start by studying the following boundary regions of the state space:
(i) The set of states with PROB(M | A1) = 1 corresponds to the front face of the unit cube.
(ii) The set of states PROB(M | A1) = 0 is shown as the back face of the unit cube.
(iii) The set of states PROB(A2) = 1 represents the right face of the cube.
(iv) The set with PROB(A2) = 0 is given by the left face of the cube.
(v) The rectangle in the interior represents the Eells-Jeffrey manifold where PROB(M | A1) = PROB(M | A2).
Let’s start with the set of states (i). If PROB(M | A2) = 0 (the bottom edge of the face), then one-boxing is perfectly correlated with the presence of the million, and so Skyrms’ law of motion tells us that the dynamics goes toward PROB(A2) = 0. Skyrms’ law of motion is also the relevant constraint when PROB(M | A2) = 1. These states are on the Eells-Jeffrey manifold: the million is sure to be in the box no matter what act is chosen. As a consequence, dPROB(A2)/dt is positive and the dynamics goes toward PROB(A2) = 1. If PROB(A2) = 1 or PROB(A2) = 0, the independence dynamics is the only force at work, driving deliberation toward the Eells-Jeffrey manifold: dPROB(M | A2)/dt is positive. The arrows in Figure 4 summarize this information.
The set of states (ii), which has PROB(M | A1) = 0, can be analyzed similarly. States with PROB(M | A2) = 1 and PROB(M | A2) = 0 both have dPROB(A2)/dt > 0 by Skyrms’ law of motion (the first because A2 is perfectly correlated with M, the second because these states are part of the Eells-Jeffrey manifold). These are shown as the top and bottom edges of the back face in Figure 4. For the two sets of states where PROB(A2) = 0 and PROB(A2) = 1, respectively, the independence dynamics flows toward the Eells-Jeffrey manifold. Figure 4 again shows the corresponding arrows.
The two remaining relevant sets of states on the boundary are of type (iii) and (iv): PROB(A2) = 1 (right face in Figure 4) and PROB(A2) = 0 (left face).31 For each, the probability of A2 is fixed, and so the independence dynamics is the only qualitative constraint on the dynamics for these two sets of states. It implies that trajectories broadly tend toward states with PROB(M | A1) = PROB(M | A2) (the diagonals on the faces). The behavior of the dynamics can be specified further under assumptions that go beyond the independence dynamics and Skyrms’ law of motion. I will give a plausible specification below, but one conclusion follows from what has already been said: the dynamics flows toward the Eells-Jeffrey manifold. The same tendency is at work in the interior of the state space (that is, all states for which PROB(A2), PROB(M | A2) and PROB(M | A1) are strictly between zero and one). Note also that along the interior of the Eells-Jeffrey manifold (throughout which PROB(M | A1) = PROB(M | A2)), the dynamics tends toward the set of states with PROB(A2) = 1 for the same reason as in the two-dimensional model: once independence between acts and states is in place, the evidential expected value of A2 is larger than that of A1, and so, by Skyrms’ law of motion, PROB(A2) increases.
These observations are sufficient to arrive at the main conclusion: that the decision maker becomes certain she will choose A2. To see why, consider the two halves of the state space separated by the Eells-Jeffrey manifold: the set of states with PROB(M | A2) > PROB(M | A1) and the set of states with PROB(M | A2) < PROB(M | A1); the first set of states is represented by the part of the cube “above” the Eells-Jeffrey manifold in Figure 4, and the other half is “below”. The dynamics on the first set of states is straightforward: since A2 is positively correlated with M, trajectories go toward the set of states PROB(A2) = 1 (by Skyrms’ law of motion) while at the same time flowing toward the Eells-Jeffrey manifold, on which the dynamics also evolves to PROB(A2) = 1. Thus, the dynamics converges to the set of states with PROB(A2) = 1. The situation is a bit more nuanced for states in the other half. Since A1 is positively correlated with M, states close to the set with PROB(M | A1) = 1 may evolve toward PROB(A2) = 0 at first (by Skyrms’ law of motion). But because of the independence dynamics, these trajectories will ultimately be drawn toward the Eells-Jeffrey manifold, resulting in a flow directed at PROB(A2) = 1.
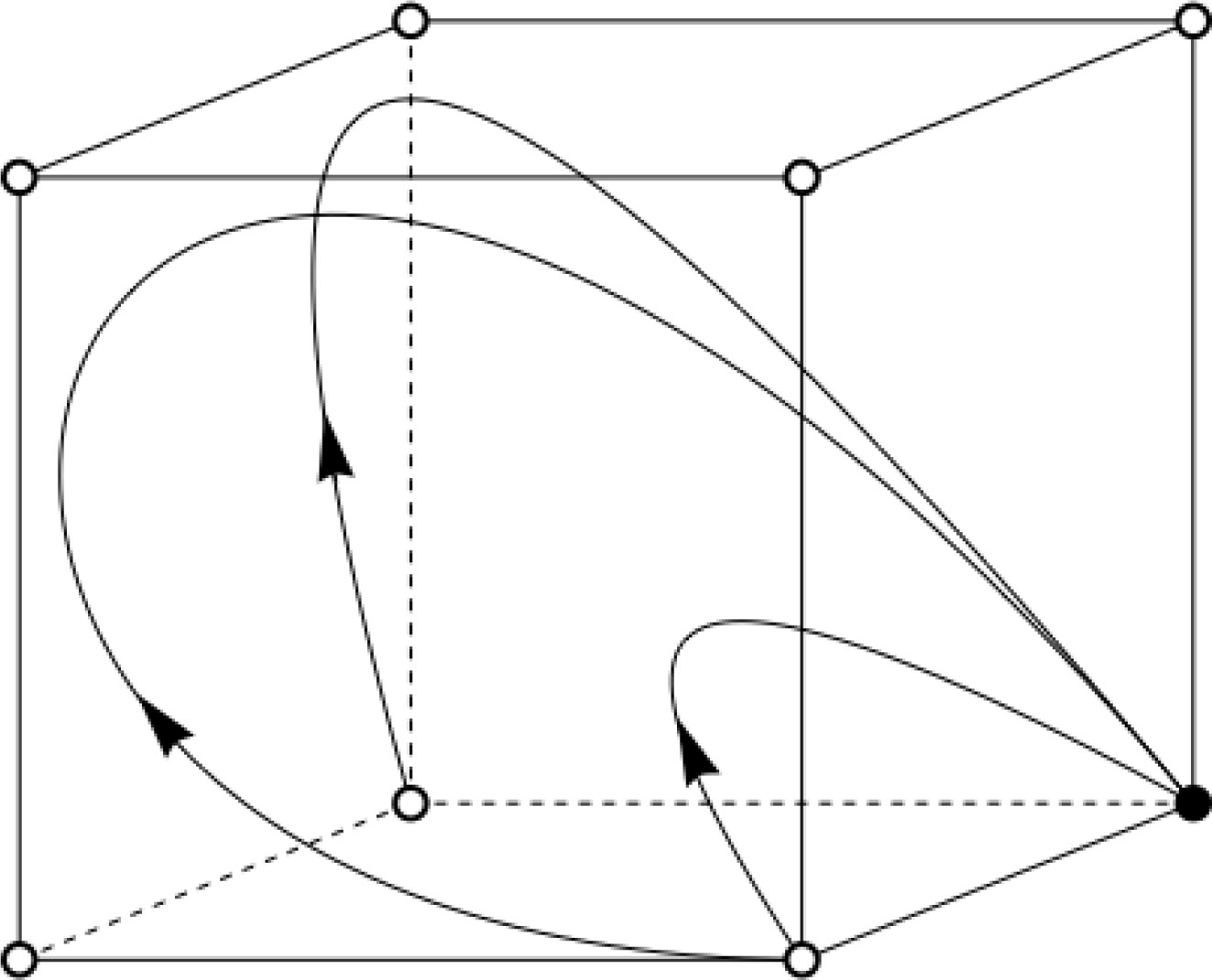
It is not difficult to read off the broad outlines of the dynamic flow from the arrows in Figure 4. The dynamics close to the boundary is continuous with the dynamics on the boundary. In the interior, Skyrms’ law of motion and the independence dynamics draw all trajectories ultimately to the set of states with PROB(A2) = 1. But what are the stable equilibria among these states? In order to have a more concrete example of how deliberation may unfold, more stipulations can be made concerning what happens when PROB(A2) = 1 and PROB(A2) = 0. This can be done in a number of ways that are broadly consistent with the independence dynamics. Here is one of them. Suppose the decision maker is certain that she will choose A2: PROB(A2) = 1. We stipulate that, in this case, the decision maker becomes increasingly certain that the million is not in the box no matter what she chooses: the deliberative dynamics goes toward PROB(M | A1) = PROB(M | A2) = 0.32 One way to implement this idea is shown on the right face of Figure 4. The diagonal line is part of the Eells-Jeffrey manifold. If the decision maker comes to believe that the million is not in the box no matter what, then deliberation carries these initial states to the state where both PROB(M | A1) and PROB(M | A2) are zero, as indicated by the arrow in Figure 4 on the diagonal of the right face. The independence dynamics pushes states off the diagonal toward the diagonal. Combining this with earlier stipulations establishes convergence to PROB(A2) = 1 and PROB(M | A2) = PROB(M | A1) = 0 on the right face of the unit cube. (On the left face, analogous assumptions can be made; I leave them out here since interior states cannot converge to the left face.) By continuity, the same is true close to the right face. Since interior states flow toward the Eells-Jeffrey manifold and thus ultimately to the right face, they also converge to the state PROB(A1) = 1, PROB(M | A1) = PROB(M | A2) = 0. Hence, as long as the independence dynamics draws deliberation toward the Eells-Jeffrey manifold in the interior and Skyrms’ law of motion is the only other force at work, there is no further equilibrium in this case. This dynamics is sketched in Figure 5.
I don’t wish to place too much emphasis on these special stipulations. There are many other plausible ways to model the dynamics on the right face (and the left face) in a way that is consistent with Skyrms’ law of motion and the independence dynamics. As we have seen above, there is generic convergence to the set of states with PROB(A1) = 1 under the two qualitative constraints. This leaves open which two-boxing states are reached in the limit. Additional stipulations narrow down the set of feasible two-boxing states, but only two-boxing states are feasible.
In what way, exactly, does the foregoing model depart from Skyrms’ dynamic treatment of metatickles? In the new model, deliberation may flow toward one-boxing first before turning around to go toward two-boxing. This happens whenever the decision maker’s beliefs are such that initially V(A1) > V(A2) and later V(A1) < V(A2). Continuity of the dynamics implies that there exists a state PROB(A2) = p at which V(A1) = V(A2). Hence dPROBP(A2)/dt = 0 at p, and so in Skyrms’ model deliberation stops at this point. In particular, states and acts remain dependent at this equilibrium. By contrast, in the new model the independence dynamics continues to operate even if V(A2) = V(A1) at a state PROB(A2) = p: the agent continues to explore her attitudes and how they might affect the evaluation of acts at such a state, while in Skyrms’ model the equality of expected values is taken as evidence that no more information is forthcoming in deliberation.
Why should a rational and sophisticated deliberator stop thinking when acts have the same expected desirabilities? As long as states and acts are correlated, deliberation about states may potentially uncover new information relevant for the decision problem. This thought can be sharpened within our new model. Suppose the dynamics initially evolves toward A2 as in Skyrms’ model, and assume the independence dynamics is at rest as soon as the two acts, A1 and A2, have the same expected desirability. Hence there exists a rest point in the interior of the cube (or the square) immediately before PROB(A2) starts to increase (as in the lower halves of Figures 3 and 5). This rest point cannot be stable, though. A slight perturbation toward the Eells-Jeffrey manifold increases the expected desirability of A2 relative to A1, allowing deliberation to proceed toward choosing A2. The model of generalized rational deliberation reveals the fragility of the state of indecision in Skyrms’ model.
Summing up, there exist plausible versions of deliberative evidential decision theory that agree with causal decision theory in Newcomb’s problem. Since the assumptions that guide deliberation are of a broad, qualitative nature, they apply to a large class of dynamical models of deliberation, meaning that the results arrived at here are robust.33
6. Metatickles Assessed
David Lewis argued that Eells’ metatickle argument is of limited relevance:
One thing to note in response is that similar things can be said about any normative decision theory, including causal decision theory. Adopting credences for dependency hypotheses, for instance, requires one to discern and weigh all relevant causal relationships, which might also prove to be too challenging for less than ideally rational agents.I reply that the Tickle Defence does establish that a Newcomb problem cannot arise for a fully rational agent, but that decision theory should not be limited to apply only to the fully rational agent. Not so, at least, if rationality is taken to include self-knowledge. May we not ask what choice would be rational for the partly rational agent, and whether or not his partly rational methods of decision will steer him correctly? A partly rational agent may very well be in a moderate Newcomb problem, either because his choices are influenced by something besides his beliefs and desires or because he cannot quite tell the strengths of his beliefs and desires before he acts.34
The larger issue at play is a methodological one. What is the right level of idealization when discussing normative aspects of decision theories? Boundedness considerations cannot be ignored when we think of a theory as applied to, say, human agents. For other purposes, though, we do meet a decision theory on its own turf. We may think of a decision theory as a formal structure that provides recommendations to agents regardless of whether they are always willing and able to adopt the theory. The advantage of this perspective is that we can compare best versions of decision theories—in our case, causal and evidential decision theory—as to which ones provide better guides for agents. Whether and to what extent agents can use the theory is an important but conceptually distinct issue. Thus, when augmenting evidential decision theory with metatickles, what we want to know is whether a sophisticated version of the theory agrees with causal decision theory and not, as Lewis seems to suggest, whether this happens for an agent not fully capable of executing the theory.35
Furthermore, the assumption that one has introspective access to one’s beliefs and desirabilities that underlies deliberative decision theory is perhaps less problematic than it’s sometimes thought to be. Stalnaker made the following point in epistemic game theory:
The same point applies to deliberative decision theory. A deliberator has introspective access to probabilities and desirabilities, but just as the latter can be unconscious and inarticulate, the processing of those beliefs during reflective deliberation need not be fully conscious or articulate.It is not clear how one acts on one’s beliefs if one does not have introspective access to them. Some may object to the introspective assumption on the ground that a person may have unconscious or inarticulate beliefs, but the assumption is not incompatible with this: if beliefs can be unconscious, so can beliefs about beliefs. It is not assumed that one knows how to say what one believes.36
The most serious questions for the metatickle approach advocated here are raised by the independence dynamics. Does deliberation always lead to the Eells-Jeffrey manifold? My answer is no. A tendency toward the Eells-Jeffrey manifold is to be expected if one believes that deliberation generates information; a complete, or nearly complete, approach is to be expected if one believes, in addition, that one’s probabilities and desirabilities eventually capture all information about acts and states. Deliberation, however, does not always generate information (if deliberation cycles, information need not increase); and there might be evidence about states and acts that cannot be accessed by deliberation, as is the case if you believe that the predictor in Newcomb’s problem knows more about how you make decisions than you do yourself. In the present context, in which one is assumed to have access to one’s attitudes, this requires that one believes how one chooses acts is not fully captured by how one evaluates them in light of ones maximally informed probabilities and desirabilities.
Prima facie, there is nothing irrational about such beliefs. How an agent makes decisions need not be fully transparent to herself even if she has introspective access to metatickles. In such cases, someone who knows more about the agent than she does herself can have access to evidence about how the agent will act that is outside the agent’s reach. That evidence can be used to make a prediction that the agent herself believes to be more reliable than what she can infer from a fully informed metatickle.
That said, an agent who believes that there are hidden factors influencing her choice behavior finds herself in a peculiar situation. Let us say that a decision maker acts with integrity if her choice of act is based purely on her credences, utilities, and a decision rule that she regards as providing the correct normative standard.37 Thus, an agent with a maximally informed metatickle that fails to screen off acts from states does not consider herself to be acting with integrity.38 Instead, she believes that her choice is influenced by factors other than her desires, beliefs and what she takes to be the correct standard of evaluating acts (in this case, evidential decision theory).
This line of thought can be sharpened by observing that it bears some resemblance to Ramsey’s Thesis. Ramsey states that
This suggests that there is a special agential perspective for one’s own acts: if you conceive an act as being under your control, then it needs to be evidentially independent of the past for you before you act (it doesn’t need to be evidentially independent of the past for others, or for you at a later time). Ramsey’s Thesis has given rise to a lively debate in decision theory.40 What’s important for us here is that, if correct, the thesis leads to a similar kind of reconciliation between causal and evidential decision theory as Eells’ metatickle approach. In Newcomb’s problem, whether the million is in the box was fixed by the predictor in the past. If your present choice of act does not provide (for you, now) any information about the past, then the acts of choosing one or two boxes are independent of states.any possible present volition of ours is (for us) irrelevant to any past event. To another (or to ourselves in the future) it can serve as a sign of the past, but to us now what we do affects only the probability of the future.39
The reconciliation developed in this paper is more modest in scope than the one based on Ramsey’s Thesis. It does not claim that acts are never evidentially relevant to past events for the decision maker. Instead, the metatickle approach restricts evidential independence of states and acts to situations that are the most natural setting for decision theory: those in which an agent acts with integrity. If integrity fails, an agent’s decision theoretic evaluations are compromised. She is of two minds: a transparent one within which her decision theory operates, and a realm of hidden factors influencing final choices. The hidden realm has the agent look at herself as an observer, not as acting based solely on her reasons for choosing acts as captured by the metatickle, leaving her in a middle ground between Ramsey’s Thesis and the perspective of an investigator for whom the choice of an act is just a piece of evidence like any other.
Deliberational dynamics has the conceptual resources to shed light on this middle ground. Questions of timing and the details of the deliberative process become crucial. For instance, in Newcomb’s problem it is not necessary to converge to the Eells-Jeffrey manifold in order to end up choosing two boxes. If the decision maker starts out with a belief that choosing one box is strongly correlated with the million having been stashed, screening off by the metatickle only has to become strong enough for the dynamics to turn around, in which case the process can converge to choosing two boxes without also converging to the Eells-Jeffrey manifold. Whether or not this happens will depend on the details of an agent’s deliberative dynamics, in particular the strength of the independence dynamics relative to the dynamics governed by Skyrms’ law of motion. This gives rise to a rich set of questions about different types of rational deliberation and their significance for decision theory.
7. Conclusion
We have seen that the reconciliation Eells and Jeffrey had in mind can work if a decision maker acts with integrity. In other cases it may fail, depending on the degree to which evolving metatickles screen off states from acts: if deliberation comes sufficiently close to the Eells-Jeffrey manifold, then it converges to two-boxing; otherwise it does not.
Remaining far off the Eells-Jeffrey manifold—even toward the end of deliberation—leaves the decision maker in an uncomfortable epistemic position. She does not expect rational deliberation to result in a state in which her reasons to act (the metatickle) capture all the information acts give about states: a part of her decision making faculty is outside the agent’s decision theoretic evaluations. She also believes this can be exploited by an external agent who has more information about how she makes decisions than she does herself. So, while the reconciliation through metatickles is imperfect, it does fail in special kinds of situations: those in which the decision maker believes that she is not going to be fully effective as an agent.
The loss of effectiveness is not restricted to evidential decision theory. A sophisticated causal decision maker also has metatickles, raising the question of whether a causal deliberative process reaches the Eells-Jeffrey manifold. If not, the causal decision theorist finds herself in the same disquieting epistemic place as the evidential decision theorist. The causalist, however, cuts through the Gordian knot by making choices relative to her unconditional probabilities of states. Still, in the relevant cases the causal decision theorist does so without believing that nothing but her probabilities and desires determines her decisions. The causalist may choose correctly for the wrong reasons.
Acknowledgements
Many thanks to Arif Ahmed, Brad Armendt, Sara Aronowitz, Richard Bradley, Adam Elga, Daniel Herrmann, Jim Joyce, Saira Khan, Calum McNamara, Gerard Rothfus, Hannah Rubin, Snow Zhang, and Kevin Zollman, as well as two anonymous reviewers for helpful comments.
Special thanks to Melissa Fusco and Brian Skyrms for formative discussions.
Notes
- This is not to say that there are no differences between Aristotelian deliberation and decision theory. While decision theory takes a range of acts as given, Aristotle sketches a backward discovery procedure that reasons from the ends one would like to achieve back to the means; see Karen M. Nielsen, “Deliberation as Inquiry: Aristotle’s Alternative to the Presumption of Open Alternatives,” Philosophical Review 120 (2011), and Agnes Callard, “Aristotle on Deliberation,” in Ruth Chang and Kurt Sylvan (eds.), Routledge Handbook of Practical Reason (Routledge, 2020). ⮭
- Richard C. Jeffrey, The Logic of Decision (Chicago: University of Chicago Press, 1983). ⮭
- The subjunctive causal decision theory of Gibbard and Harper is based on Stalnaker’s theory of conditionals; see Allan Gibbard and William L. Harper, “Counterfactuals and two Kinds of Expected Utility,” in W. L. Harper, R. Stalnaker, and G. Pearce (eds.), Ifs: Conditionals, Beliefs, Decision, Chance, and Time (Dordrecht: Reidel, 1981), and Robert C. Stalnaker, “A Theory of Conditionals,” in N. Rescher (ed.), Studies in Logical Theory. American Philosophical Quarterly Monographs 2 (Oxford: Blackwell, 1968). The theories of Lewis and Skyrms are non-subjunctive; see David Lewis, “Causal Decision Theory,” Australasian Journal of Philosophy 59 (1981), and Brian Skyrms, Pragmatics and Empiricism (New Haven: Yale University Press, 1984). Joyce argues that these theories are effectively equivalent; see James M. Joyce, The Foundations of Causal Decision Theory (Cambridge: Cambridge University Press, 1999). ⮭
- See Arif Ahmed, Evidence, Decision and Causality (Cambridge: Cambridge University Press, 2014), and Caspar Hare and Brian Hedden, “Self-Reinforcing and Self-Frustrating Decisions,” Noûs 50 (2015). ⮭
- Ellery Eells, “Causality, Utility, and Decision,” Synthese 48 (1981), Ellery Eells, Rational Decision and Causality (Cambridge: Cambridge University Press, 1982), Ellery Eells, “Metatickles and the Dynamics of Deliberation,” Theory and Decision 17 (1984). See also Richard C. Jeffrey, “The Logic of Decision Defended,” Synthese 48 (1981). A quite different approach to reconciliation is developed in Huw Price, “Agency and Probabilistic Causality,” The British Journal for the Philosophy of Science 42 (1991). ⮭
- See e.g. Lewis, op. cit., Teddy Seidenfeld, “Comments on Causal Decision Theory,” in PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association, Cambridge University Press (1984), Joyce, The Foundations of Causal Decision Theory, and Ahmed, op. cit.. ⮭
- Brian Skyrms, “Causal Decision Theory,” The Journal of Philosophy 79 (1982) and Skyrms, Pragmatics and Empiricism. ⮭
- See Leonard J. Savage, The Foundations of Statistics (New York: Wiley, 1954). ⮭
- This is not to suggest that Savage’s decision theory is neither causal nor evidential, but only that in Savage’s theory acts are not assigned probabilities. See James M. Joyce, “Levi on Causal Decision Theory and the Possibility of Predicting One’s Own Actions,” Philosophical Studies 110 (2002) for a discussion. ⮭
- Jeffrey, The Logic of Decision. ⮭
- There is a debate over whether probabilities can be meaningfully assigned to acts, i.e. whether deliberation crowds out prediction; see, inter alia, Wolfgang Spohn, “Where Luce and Krantz do Really Generalize Savage’s Decision Model,” Erkenntnis 11 (1977), Isaac Levi, The Covenant of Reason: Rationality and the Commitments of Thought (Cambridge, 1997), Wlodek Rabinowicz, “Does Practical Deliberation Crowd out Self-Prediction?,” Erkenntnis 57 (2002), Alan Hájek, “Deliberation Welcomes Prediction,” Episteme 13 (2016), and Katia Vavova, “Deliberation and Prediction: It’s Complicated,” Episteme 13 (2016). I will set this debate aside here and proceed on the natural assumption that it is possible to assign probabilities to one’s own future acts during deliberation. ⮭
- Lewis, op. cit.. The K-partition approach of Skyrms, Pragmatics and Empiricism is similar. ⮭
- For simplicity, we assume that monetary outcomes fully reflect the decision maker’s preferences. ⮭
- See Eells, Causality, Utility, and Decision, Eells, Rational Decision and Causality, and Eells, Metatickles and the Dynamics of Deliberation. ⮭
- Eells, Rational Decision and Causality, p. 139 ⮭
- Jeffrey, The Logic of Decision Defended, p. 486. ⮭
- See discussions in, e.g., Lewis, op. cit., Paul Horwich, “Decision Theory in the Light of Newcomb’s Problem,” Philosophy of Science 52 (1985), Joyce, The Foundations of Causal Decision Theory, Seidenfeld, op. cit. and Ahmed, op. cit.. ⮭
- To be fair, Eells did discuss a number of possibilities in his more detailed versions of the argument, e.g. his attempt to distinguish between conscious and unconscious beliefs in Eells, Rational Decision and Causality, Chapter 7. ⮭
- See Skyrms, Pragmatics and Empiricism. ⮭
- See James M. Joyce, “Regret and Instability in Causal Decision Theory,” Synthese 187 (2012); on this point, see also Frank Arntzenius, “No Regrets, or: Edith Piaf Revamps Decision Theory,” Erkenntnis 68 (2008) and Greg Lauro and Simon M. Huttegger, “Structural Stability in Causal Decision Theory,” Erkenntnis 87 (2022). The epistemic aspect Joyce alludes to remains largely hidden in Newcomb’s problem. A causal decision theorist may adjust her probabilities for states based on information provided by her act, but this has no effect on causal expected utilities in Newcomb’s problem because choosing one box is worse than choosing two boxes no matter one’s probabilities for states. This issue is discussed in Joyce, The Foundations of Causal Decision Theory and Melissa Fusco, “Epistemic Time Bias in Newcomb’s Problem,” in Arif Ahmed (ed.), Newcomb’s Problem (Cambridge: Cambridge University Press, 2018). ⮭
- Armendt develops an account of rational deliberation for causal decision theory that departs from the full information maxim. A rational decision maker may stop deliberation if she must (due to costs or other constraints). The idealized setting sketched here is a limiting case. See Brad Armendt, “Causal Decision Theory and Decision Instability,” The Journal of Philosophy 116 (2019). ⮭
- See Skyrms, Causal Decision Theory and Skyrms, Pragmatics and Empiricism. In addition to Skyrms’ law of motion, a dynamics has to be defined such that states are always probabilities. We shall assume this throughout the paper. ⮭
- A corresponding class of causal deliberative models leads to choosing two boxes. See Skyrms, Causal Decision Theory. ⮭
- E.g. Joyce, Regret and Instability in Causal Decision Theory. Probability kinematics is also known as Jeffrey conditioning. See Jeffrey, The Logic of Decision. ⮭
- Skyrms, Pragmatics and Empiricism, p. 77 suggests that the conditional probabilities vary continuously in PROB(A2) and in time. Since time doesn’t play a role in his argument, I’ll ignore it here. ⮭
- Jeffrey discusses this in the context of the Prisoner’s Dilemma: “Then in knowing my decision—my preference between ratting and not ratting as deliberation ends—I know nearly as much about his [the other prisoner’s] choice as I will know when I have acted.” See Jeffrey, The Logic of Decision Defended, p. 486. In Eells’ case the assumption is plausible given his original account of the metatickle defense, which assumes that the agent is certain about her beliefs and desirabilities near the time of decision (Eells, Rational Decision and Causality, p. 144). In his response to Skyrms he is more explicit: “At this moment [the moment of choice], it is natural to think that, as a result of the agent’s deliberations, Pr(A2) will be either very close to 1 or very close to 0.” See Eells, Metatickles and the Dynamics of Deliberation, p. 79. ⮭
- Skyrms, Causal Decision Theory, p. 704. Skyrms, Pragmatics and Empiricism shows that there are similar problems for other models of evidential deliberation. ⮭
- Eells, Metatickles and the Dynamics of Deliberation. ⮭
- Aside from this, it is unclear whether urgency to act on its own really does result in two-boxing rather than one-boxing. ⮭
- There is a small caveat concerning the rest point being a global attractor. Under many deliberational dynamics, such as Skyrms’ Bayes dynamics, the boundary is invariant under the dynamics: no initial state on the boundary gives rise to a trajectory in the interior. But even in that setting the rest point attracts almost all initial states, namely those in the interior. See Brian Skyrms, The Dynamics of Rational Deliberation (Princeton: Princeton University Press, 1990) ⮭
- The dynamics on the bottom and top faces follows from the boundary constraints for the other four faces. ⮭
- As in the two-dimensional model, the technical difficulty of working with conditional probabilities given propositions with probability zero can be overcome by considering the dynamics close the the set of states with PROB(A2) = 1 and requiring the dynamics on the set of states with PROB(A2) = 1 to be continuous with what happens close to it. ⮭
- The results continue to hold under a wide range of modifications. For example, neither the Eells-Jeffrey manifold nor the faces of the cube need to be strictly invariant under deliberational dynamics. Similarly, the independence dynamics does not need to operate in exactly the way I stipulated. What is important is that the dynamics approximates these assumptions. ⮭
- Lewis, op. cit., p. 10. ⮭
- One need not think, as Lewis suggests, that full rationality requires self-knowledge. In this case, the point just made still applies. If one wishes to compare decision theories as guides, as I do here, the question of whether rationality requires self-knowledge is beside the point. Being guided by a decision theory requires providing it with, and thus having access to, the inputs it needs to calculate expected utilities. ⮭
- Robert C. Stalnaker, “Knowledge, Belief and Counterfactual Reasoning in Games,” Economics and Philosophy 12 (1996), pp. 140-41. ⮭
- For the present discussion, the decision rule is maximizing expected desirability. In case of ties we assume that the agent has a tie breaking rule. This is irrelevant for Newcomb’s problem, but it is important in decision problems with decision instability. See Gibbard and Harper, op. cit., Andy Egan, “Some Counterexamples to Causal Decision Theory,” The Philosophical Review 116 (2007), Arntzenius, op. cit., and Joyce, Regret and Instability in Causal Decision Theory. ⮭
- If the maximally informed metatickle leaves the agent far from the Eells-Jeffrey manifold, the agent may end up one-boxing. ⮭
- Frank P. Ramsey, “General Propositions and Causality,” in D. H. Mellor (ed.), Philosophical Papers (Cambridge: Cambridge University Press, 1990), p. 145. ⮭
- See, inter alia, Price, Agency and Probabilistic Causality, Huw Price, “The Direction of Causation: Ramsey’s Ultimate Contingency,” Philosophy of Science Association 2 (1993), and Ahmed, op. cit., Chapter 8. Another approach close to Ramsey’s Thesis is developed in Christopher Meek and Clark Glymour, “Conditioning and Intervening,” The British Journal for the Philosophy of Science 45 (1994). Meek and Glymour distinguish between conditioning and intervening within the framework of causal Bayes nets. ⮭
References
Ahmed, Arif Evidence, Decision and Causality. Cambridge: Cambridge University Press, 2014
Armendt, Brad “Causal Decision Theory and Decision Instability” The Journal of Philosophy 116 (2019): 263–277
Arntzenius, Frank “No Regrets, or: Edith Piaf Revamps Decision Theory” Erkenntnis 68 (2008): 277–297
Callard, Agnes “Aristotle on Deliberation” In Ruth Chang and Kurt Sylvan (eds.), Routledge Handbook of Practical Reason. Routledge, 2020: 126–140
Eells, Ellery “Causality, Utility, and Decision” Synthese 48 (1981): 295–329
Eells, Ellery Rational Decision and Causality. Cambridge: Cambridge University Press, 1982
Eells, Ellery “Metatickles and the Dynamics of Deliberation” Theory and Decision 17 (1984): 71–95
Egan, Andy “Some Counterexamples to Causal Decision Theory” The Philosophical Review 116 (2007): 93–114
Fusco, Melissa “Epistemic Time Bias in Newcomb’s Problem” In Arif Ahmed (ed.), Newcomb’s Problem. Cambridge: Cambridge University Press, 2018: 73–95
Gibbard, Allan and William L. Harper “Counterfactuals and two Kinds of Expected Utility” In W. L. Harper, R. Stalnaker, and G. Pearce (eds.), Ifs: Conditionals, Beliefs, Decision, Chance, and Time. Dordrecht: Reidel, 1981: 153–190
Hájek, Alan “Deliberation Welcomes Prediction” Episteme 13 (2016): 507–528
Hare, Caspar and Brian Hedden “Self-Reinforcing and Self-Frustrating Decisions” Noûs 50 (2015): 604–628
Horwich, Paul “Decision Theory in the Light of Newcomb’s Problem” Philosophy of Science 52 (1985): 431–450
Jeffrey, Richard C. “The Logic of Decision Defended” Synthese 48 (1981): 473–492
Jeffrey, Richard C. The Logic of Decision. Chicago: University of Chicago Press, 1983 3rd revised edition
Joyce, James M. The Foundations of Causal Decision Theory. Cambridge: Cambridge University Press, 1999
Joyce, James M. “Levi on Causal Decision Theory and the Possibility of Predicting One’s Own Actions” Philosophical Studies 110 (2002): 69–102
Joyce, James M. “Regret and Instability in Causal Decision Theory” Synthese 187 (2012): 123–145
Lauro, Greg and Simon M. Huttegger “Structural Stability in Causal Decision Theory” Erkenntnis 87 (2022): 603–621
Levi, Isaac The Covenant of Reason: Rationality and the Commitments of Thought. Cambridge, 1997
Lewis, David “Causal Decision Theory” Australasian Journal of Philosophy 59 (1981): 5–30
Meek, Christopher and Clark Glymour “Conditioning and Intervening” The British Journal for the Philosophy of Science 45 (1994): 1001–1021
Nielsen, Karen M. “Deliberation as Inquiry: Aristotle’s Alternative to the Presumption of Open Alternatives” Philosophical Review 120 (2011): 383–421
Price, Huw “Agency and Probabilistic Causality” The British Journal for the Philosophy of Science 42 (1991): 157–176
Price, Huw “The Direction of Causation: Ramsey’s Ultimate Contingency” Philosophy of Science Association 2 (1993): 253–267
Rabinowicz, Wlodek “Does Practical Deliberation Crowd out Self-Prediction?” Erkenntnis 57 (2002): 91–122
Ramsey, Frank P. “General Propositions and Causality” In D. H. Mellor (ed.), Philosophical Papers. Cambridge: Cambridge University Press, 1990: 145–163
Savage, Leonard J. The Foundations of Statistics. New York: Wiley, 1954
Seidenfeld, Teddy “Comments on Causal Decision Theory” In PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association Cambridge University Press. 1984: 201–212
Skyrms, Brian “Causal Decision Theory” The Journal of Philosophy 79(1982): 695–711
Skyrms, Brian Pragmatics and Empiricism. New Haven: Yale University Press, 1984
The Dynamics of Rational Deliberation. Princeton: Princeton University Press, 1990
Spohn, Wolfgang “Where Luce and Krantz do Really Generalize Savage’s Decision Model” Erkenntnis 11 (1977): 113–134
Stalnaker, Robert C. “A Theory of Conditionals” In N. Rescher (ed.), Studies in Logical Theory. American Philosophical Quarterly Monographs 2. Oxford: Blackwell, 1968: 98–112
Stalnaker, Robert C. “Knowledge, Belief and Counterfactual Reasoning in Games” Economics and Philosophy 12 (1996): 133–163
Vavova, Katia “Deliberation and Prediction: It’s Complicated” Episteme 13 (2016): 529–538