1. Introduction
There is much that remains mysterious about Euclid and his seminal work The Elements. Many modern mathematicians think of Euclid as pursuing (or even inventing) something like the modern axiomatic method, albeit crudely. But whether this sort of understanding of Euclid is accurate or anachronistic is a challenging question. The Elements itself offers little guidance on the matter. Even in modern, highly formal mathematical texts the author will typically give some sort of preamble to orient the reader with respect to the goals and methods of what is to follow. Dissappointingly, nothing of this sort happens in The Elements. Euclid simply presents us with a list of definitions, a list of postulates, and a list of so-called ‘common notions’, and then begins his proofs. The definitions, postulates and common notions are not referenced when they are later used—in fact, many definitions are not used in any obvious way anywhere in the text, and many of the proofs appear to rely on principles that are not contained in the definitions, postulates or common notions. As a result, questions about Euclid’s broader goals, and his general conception of mathematics and its methodology, are left completely open. There is consequently something unavoidably speculative about all attempts to place The Elements in a broader philosophical—or even mathematical—framework. It is in this unabashed spirit of speculation that I too shall need to proceed.
Euclid’s five postulates will be one of my main points of interest. They are as follows:1
Postulate 1: Let the following be postulated: to draw a straight line from any point to any point.
Postulate 2: To produce a finite straight line continuously in a straight line.
Postulate 3: To describe a circle with any centre and distance.
Postulate 4: That all right angles are equal to one another.
Postulate 5: That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
What sort of thing are these postulates, and what role are they supposed to play? They are clearly supposed to be basic principles from which the theorems of the Elements can be deduced (on some conception or other of deduction).2 But basic in what sense? In a paper on the nature of mathematical postulates Feferman (2000) quotes the OED as telling us that a postulate is ‘a self-evident proposition requiring no formal demonstration to prove its truth, but received and assented to as soon as mentioned.’ Kline also somewhat controversially suggests:
Because the Greeks sought truths and had decided on deductive proof, they had to obtain postulates that were themselves truths. They did find truths whose truth was self-evident to them… . Plato applied his theory of anamnesis, that we have had direct experience of truth in a period of existence as souls in another world before coming to earth, and we have but to recall this experience to know that these truths included the postulates of geometry. (1972)
In the spirit of these views, are Euclid’s postulates supposed to be a set of self-evident claims on which the discipline of geometry is then based? Or, at the other extreme, do the postulates just represent a more or less arbitrary starting point from which we may begin the mathematical business of proving the theorems of geometry, with no claim that they have any special sort of epistemic status, and no claim that they are obvious in any particular way?
There are reasons, I think, to be unhappy with both of these extremes. While some of Euclid’s postulates could perhaps be regarded as self-evident, it is far from clear that this could be said of Postulate 5 (the so-called ‘Parallel Postulate’). Moreover, in other mathematical works of Euclid—such as his Optics (Burton 1945)—the basic assumptions from which his derivations proceed seem even less immediate. There is thus little historical or textual reason to think that the mathematical practice of the Greeks demanded that mathematics only proceed from something like ‘self-evident’ starting points.3
But to give up on the idea that there is anything epistemically special at all about Euclid’s postulates also seems wrong-headed (or at least, so I shall argue.) There are many different senses, after all, in which a statement may turn out to occupy an epistemically privileged position.
The challenge then is to identify some sense in which, even though Euclid’s postulates fall short of being self-evident truths, they nevertheless represent genuine starting points for the mathematical practice they define. Meeting this challenge will be a large part of the goal of this paper.
Our investigations here will also connect (albeit somewhat loosely) with another puzzling aspect of the Elements. In modern mathematical language, a statement of something like the Pythagorean Theorem might go as follows:
Pythagoras’s Theorem: Let ∆ABC be a right angled triangle with AB the hypotenuse and C the vertex at which the right angle lies. Suppose that the sides CB, CA and AB of the triangle have lengths a, b and c respectively. Then a2 + b2 = c2.
In this statement of the theorem, it is simply presupposed that each leg of the triangle is associated with a unique real number giving its length. The main content of the theorem—that a2 + b2 = c2—is then a claim that a certain mathematical relation holds between these real numbers.
Indeed, in most modern mathematical presentations of Euclidean geometry, it is simply assumed that Euclidean space is a metric space, and thus that all geometric line segments have corresponding lengths given by a real number. This metrical structure then provides us with a criterion for when two line segments have equal lengths, or when one is greater in length than another. The same sort of assumption is typically made of angles—in modern presentations of geometry, it is simply assumed that to each geometrical angle, there corresponds some real number between 0 and 2π giving the magnitude of the angle. This magnitude then similarly provides us with a criterion for the equality or inequality of angles. Likewise for areas, and so on. As in the example of the Pythagorean Theorem given above, modern presentations of geometry then tend to present their theorems as facts about the mathematical relations that hold between these quantities themselves. (Think of theorems such as that the area of a circle is given by A = πr2, or that the magnitudes of the angles of a triangle α, β and γ satisfy α + β + γ = 180°.)
What is interesting about Euclid, however, is that he does not present his theorems in this way. Whenever he can, Euclid states his theorems as facts about the relations that hold between geometrical objects themselves, rather than as facts about the relations that hold between mathematical quantities that may be associated with those geometrical objects. So for example, in Book I Proposition 47 of the Elements, Euclid states Pythagoras’s Theorem as follows:
Pythagoras’s Theorem: In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
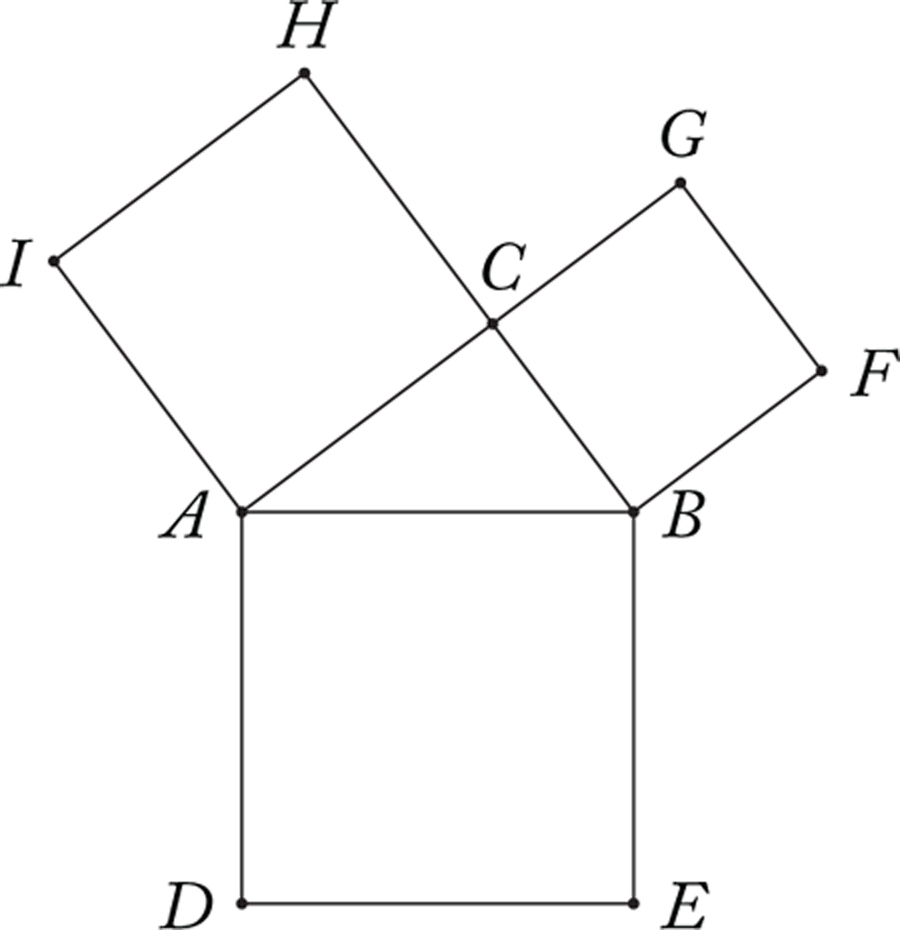
The following sort of figure then accompanies the theorem:
Here, we suppose that CAIH, CBFG and ABED are squares constructed on CA, CB, and AB respectively. In Euclid’s formulation, the Pythagorean Theorem is not first and foremost a theorem connecting three real numbers a, b and c, but rather a theorem connecting three geometric objects, namely, the squares CAIH, CBFG and ABED. An inspection of Euclid’s proof shows that in stating that the square ABED is equal to the squares CAIH and CBFG, Euclid does not mean that there are mathematical quantities (i.e., real numbers) corresponding to the areas of each of these squares such that one of these real numbers is the sum of the other two, but rather something like that the two smaller squares can be decomposed and re-assembled to form the larger square.4 In this way, Euclid’s version of Pythagoras’s Theorem is then a statement with purely geometric content. At no point in the statement or proof of Pythagoras’s Theorem, or any theorem on which it depends, is it assumed that lengths, angles or areas correspond to numerical quantities.5
Why does Euclid present his theorems this way? It is not that the very idea of associating physical magnitudes with numbers was somehow foreign. To the contrary, the Greeks had a well developed set of units of measurement and many sophisticated measuring instruments. In such measurements, quantities were unproblematically associated with geometrical objects in the natural world. Of course, it is certainly true that Euclid did not have the notation to write something as compact as the equation a2 + b2 = c2. But it is difficult to see this as a barrier to viewing geometry as a science that first and foremost tells us the relations that hold between certain sorts of quantities or numbers. Indeed, in the Chinese or Indian ancient mathematical traditions geometrical results were typically presented as relations holding between numerical quantities. (See for example Kangshen, Crossley, & Lun 1999.) It would thus be hard to argue that for some reason or other one should expect early mathematical traditions to present geometrical results in something like the manner of Euclid.
The hypothesis I would like to advance is that the very idea that lengths, angles and areas can be compared is one that Euclid and his contemporaries took not to be given, but rather to require justification. Instead of beginning with a framework in which geometrical objects are associated with mathematical quantities from the start, Euclid deliberately works in a sparser framework in which the science of comparing lengths, angles and areas both needs to be and can be grounded. In fact, I will argue that there is a straightforward way in which Euclid’s five postulates may be seen as grounding such a science of comparisons, and that this leads to an interpretation of Euclid’s postulates as something like conditions for the possibility of comparison of lengths, angles and areas. In this way, Euclid’s postulates, while not ‘self-evident’ (or ever intended to be), are nevertheless epistemologically privileged as conditions for the possibility of a type of science of measurement.6
Quite remarkably, Euclid (and perhaps his contemporaries) also notice that such a science of measurement, appropriately grounded, enables us not only to make specific claims about the equality or inequality of specific lengths, angles or areas, but also general claims about more general geometrical configurations—what I will call ‘general measurements’. While measurements of specific lengths, angles or areas can be done with traditional measuring instruments, general measurements are performed via proofs. For Euclid and his contemporaries then, proof then turns out to be first and foremost a way of making such general measurements, as opposed to a device for producing some sort of certainty about facts that are perhaps already known. This paper will largely be devoted to elaborating and arguing for the plausibility of this set of claims.
I will flesh out most of the details of this in §2 and §3. In §2 I will focus on techniques for comparing specific lengths, areas and angles—something that is not really the main subject of The Elements, though is intimately connected with it—and will show that the Euclid’s postulates may be seen as grounding such techniques in fairly straightforward ways. In §3 I will then turn to the use of these techniques in performing ‘general measurements’, which is indeed the core subject matter of The Elements (or so I shall argue). In §4 I will consider the question of what this tells us about Euclid’s broader conception of mathematics.
As a result of this investigation, we gain a richer understanding of the techniques of Greek mathematics and the motivations behind it. In addition, we gain a better understanding of the origin of proof—why, after all, did Greek mathematicians care to start proving things? What need was satisfied by mathematical proof? We will be in a much better position to address these questions using the results of the present investigations.
2. Comparing the Specific
In this section, we shall focus on the question of how a geometer can compare a pair of lengths, angles or areas that have in some way been given and physically lie before him. This will give us some insight into the status of Euclid’s postulates, as we will see in §2.5. A more complete understanding of the status of Euclid’s postulates that builds on this and more fully addresses the questions posed in the previous section will have to wait until §3 and §4.
2.1. The Comparison of Lengths
In Euclid’s definitions, postulates, and common notions, there is no suggestion that there there is anything intrinsic about line segments (or angles or areas) that allows us to immediately compare them, and say that one is greater than, equal to, or less than another in magnitude. How then over the course of The Elements do we end up being able to make these sorts of comparisons?
Let us begin by focusing on the case of line segments. How would a Euclidean geometer decide of two physical line segments before him which is longer, or whether they are equal in length? Nowhere in The Elements does Euclid specifically pose the problem ‘to decide of two lengths which is the greater, or whether they are the same.’ Nevertheless, techniques for making such comparisons emerge very early in The Elements, and are used repeatedly throughout the text.
When asked how we can compare the lengths of two line segments, perhaps the most natural response is that we can bring a ruler to one of the line segments, mark it, bring the marked ruler to the other line segment, and simply see which (if either) is the greater. A variant of this idea that does not involve marking involves bringing a (non-collapsible) compass to the first segment in such a way that its legs fall on the extremities of the interval, then bringing the compass to the second line segment and doing a comparison. Although there is in a sense nothing wrong with these sorts of solutions, we will first consider a different style of solution that will turn out to be more useful to Euclid, in a sense we will be able to articulate only later in §4.
Consider then the problem of comparing the lengths of two line segments by a traditional straightedge and (collapsible) compass construction. Given only such resources, and given two line segments AB and CD, how can we decide whether the length of AB is equal to the length of CD, and if their lengths are unequal, which is longer?
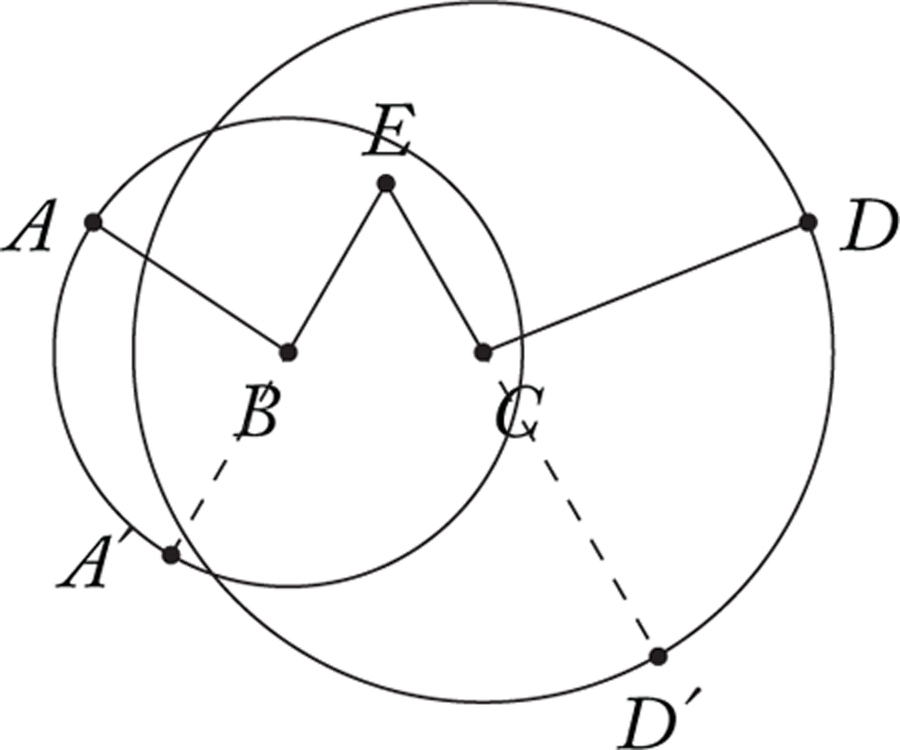
Begin by constructing a point E such that BE and CE are equal in length. This is most easily done by drawing a circle with center B and radius BC, a circle with center C and radius CB, and letting E be one of the intersection points of these two circles. These circles have equal radii. Because EB and EC are also radii of these circles, it follows that EB and EC are equal in length.
As shown below, we then then draw a circle with center B and radius BA, and extend the line segment EB until it meets this circle, calling this point of intersection A’. Then BA’ is also a radius of this circle, and so equal in length to BA. Similarly, we draw a circle with center C and radius CD, and extend the line segment EC until it meets the circle, calling this point of intersection D’. Likewise, CD and CD’ are equal in length. Using this and the fact that EB and EC are equal in length, It follows that AB is equal to (or respectively longer or shorter than) CD in length iff A’E is equal to (or respectively longer or shorter than) D’E in length.7
We have therefore reduced our problem to one of determining the relationship between the lengths of two line segments A’E, D’E that share an endpoint E. This later problem is trivial. Simply draw a circle with center E and radius EA’. If D’ lies inside the circle, then D’E is shorter than A’E, if D’ lies outside the circle, then D’E is longer than A’E, and if D’ lies on the circle, then D’E is equal in length to A’E.
In this way, we can determine the relationship between the lengths of AB and CD with a traditional straightedge and (collapsible) compass construction.
The reader will surely have noted that what has just been described is essentially the mathematical content of Book I, Propositions 1 through 3 of The Elements. That is to say, the very first thing Euclid does in The Elements is to present us with a technique for comparing the length of spatially distinct line segments. It is not merely out of love of equilateral triangles that the very first argument in the Elements shows us how to construct the equilateral triangle EBC given above; it is rather to set the stage for the algorithm just given.
Note also that the algorithm just given relies on nothing more than the ability to connect points (such as B and C) with a line segment, to extend line segments arbitrarily, and to draw circles around a given point with a given radius. That is to say, the algorithm given above uses nothing but Euclid’s Postulates 1 through 3. These facts about the existence of lines and circles are what ground the possibility of comparing lengths in the manner described. In fact, my claim is that the primary function of the postulates in The Elements is just to ground ways of comparing quantities of various kinds in various contexts in precisely this sort of way. (These comparisons will be not just between lengths, but also between angles and areas.) Spelling this argument out fully will occupy the next several sections.
2.2. The Comparison of Angles – I
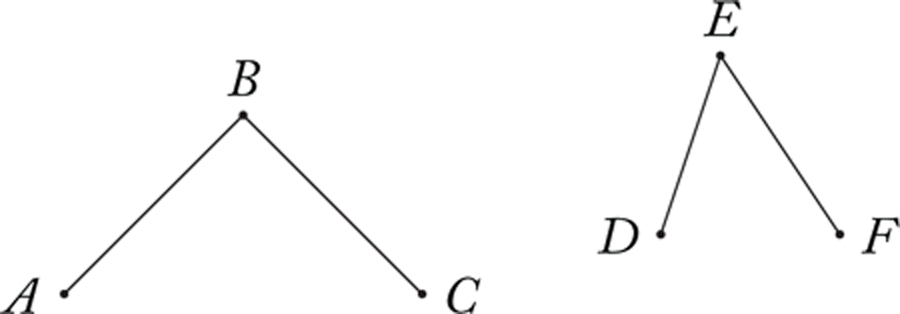
Let us turn to the question of how we can compare the magnitudes of angles. Specifically, given two angles ABC and DEF, how are we to compare them?
We consider two methods for angle comparison—one very general, and the other a method that works only for specific sorts of geometric configurations. The first method piggybacks on our method for comparing lengths—specifically, it reduces the problem of comparing angles to the problem of comparing lengths.
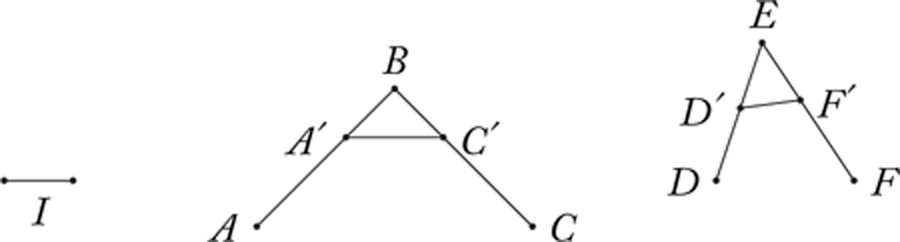
To spell out this method, we begin with an arbitrary line segment I. Along the lines segments BA, BC, ED and EF we cut off line segments equal in length to I, producing line segments BA’, BC’, ED’ and EF’ all equal in length to I. (We extend the line segments AB, BC, DE and EF if necessary to do this.)
The lengths of A’C’ and D’F’ can then be taken as measures of the sizes of the angles ABC and DEF. In particular, the angle ABC is less than, equal to or greater than the angle DEF iff the line segment A’C’ is less than, equal to or greater than the line segment D’F’ in length.8
The process of cutting off line segments equal in length to I may be done by adapting the technique presented earlier for comparing the length of line segments; this is spelt out explicitly in Book I, Proposition 3 of The Elements. The comparison of the line segments A’C’ and D’F’ may also be done using the technique presented in the previous section.
This method for comparing angles is of great importance to Euclid. In particular, in Book I Proposition 23, its main idea is used to solve the problem of constructing on a given line and a given point on that line an angle equal to another given angle. This construction is then used repeatedly in the subsequent books of The Elements.
Interestingly, Euclid does not use this method for comparing angles to define equality of angles. Instead in Book I, Propositions 24 and 25 he justifies this procedure for the comparison of angles in terms of his postulates. While the procedure in question can be carried out using the constructive tools given only in Postulates 1 through 3, justifying the claim that the procedure does what we have claimed it does turns out to rely on Postulates 1 through 3 along with the so-called method of superposition, to be discussed shortly. It does not, however, rely on Postulates 4 or 5.
2.3. The Comparison of Angles – II
While this algorithm gives us a useful way of comparing angles, it is important to realize that it is not the only method for the comparison of angles that Euclid uses. There is no particular reason why Euclid should restrict himself to only one method for comparing angles, and in fact it turns out that a quite different approach to the comparison of angles also turns out to be useful for dealing with a large class of problems in The Elements. We turn to this now.
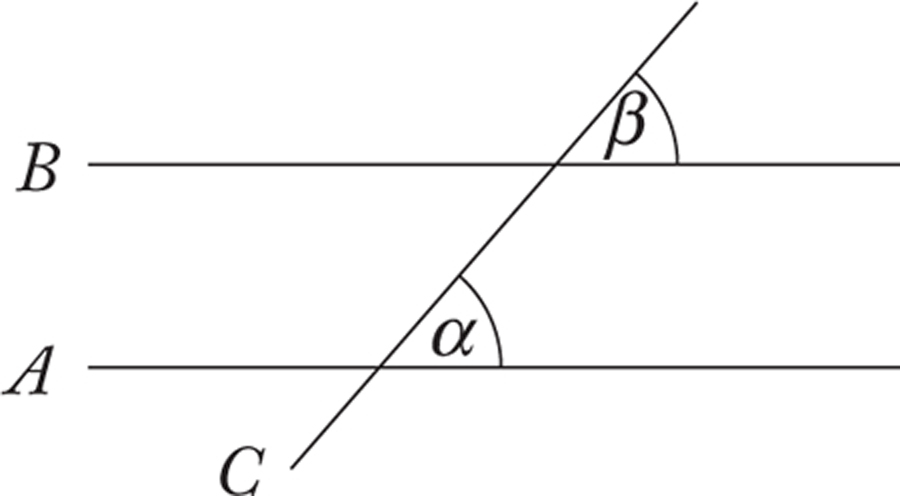
Suppose we have parallel lines A and B with a line C (a transversal) crossing both.9 Suppose the transversal C makes an angle α with the line A, and an angle β with the line B as shown.
In this case, we know that α = β. That ‘corresponding angles’ formed by a transversal cutting parallel lines are equal is perhaps the most fundamental fact about the relationship between angles formed with parallel lines, and provides us with another technique for comparing angles. This equality between angles is central to much of the work of The Elements. It plays an indispensable role in the argument that the sum of the angles of a triangle form two right angles, and much of the theory of triangles and parallelograms in general depends critically on it.
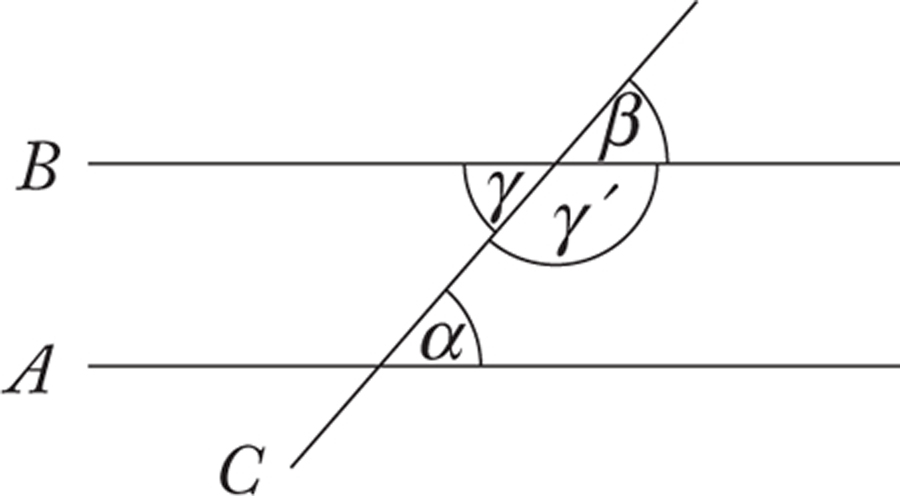
I claim that we may view the equality of corresponding angles as a tool for the comparison of angles in the special case in which these angles are formed by a transversal cutting a pair of parallel lines. It is of course primarily in the context of Euclidean geometry that it makes sense to think of this as a technique for the comparison of angles. In a geometry in which there are multiple lines B and B’ parallel to a given line A, it will not make sense to take corresponding angles to be equal in magnitude. Such an assumption would require us to say, for instance, that the angles β and β’ are equal in the situation depicted below in which B and B’ are distinct parallels to A:
The main problem is of course that angle β is a proper part of the angle β’. That nothing can be equal in magnitude to a proper part of itself is a type of reasoning that Euclid uses repeatedly throughout The Elements, and is captured in Common Notion 5, according to which ‘the whole is greater than the part.’ Thus, the magnitudes angles β and β’ cannot be identified. So for this technique for the comparison of angles to work, it must be the case that if there is a line parallel to a given line through a given point, it is unique. Now, in geometries such as spherical geometry in which parallel lines do not exist, the technique of angle comparison in question will be vacuous, because parallel lines do not exist. Thus, the most natural context in which to consider the technique of angle comparison in question is that of Euclidean geometry.
Of course, Euclid does not simply assume the equality of corresponding angles produced by a transversal cutting parallel lines, but instead argues for it explicitly in Proposition 29 of Book I. Given what has been said thus far, one might expect this argument to depend on the Parallel Postulate (Postulate 5), and indeed it does.
The argument is straightforward. It begins by showing that alternate interior angles produced by a transversal cutting a pair of parallel lines are equal. In the diagram below, consider the angles α and γ. Suppose they are unequal. Without loss of generality, suppose α > γ. Consider then the angle γ’ adjacent to the angle γ as shown. By the Parallel Postulate, α + γ’ is equal in magnitude to the sum of two right angles. It follows that γ + γ’ is less than two right angles, as α > γ. But this is a contradiction, as γ and γ’ form a straight line. Thus α and γ are equal. To show that α and β are equal, it thus suffices to show that γ and β are equal. But that opposite angles are equal is easily shown. For example, both the pair of angles γ and γ’ and the pair of angles γ’ and β form two right angles, and so eliminating the common element γ’ we have that β and γ are equal.
Note that in this argument, in addition to assuming the Parallel Postulate we have also assumed that all straight angles are equal in magnitude. Now, Euclid tends to avoid using the term ‘angle’ to describe straight angles; he typically reserves the term ‘angle’ for what we would call an angle of size < 180°. He does, however, consistently describe straight angles as the ‘sum of two right angles’ (see, for example, Book I, Propositions 13 and 14). So in Euclidean parlance, our assumption that all straight angles are equal in magnitude amounts to the claim that all right angles are equal. This assumption is of course nothing other than Euclid’s Fourth Postulate.10 In this way, the specific method for comparing angles in question presupposes both Postulates 4 and 5.
To sum up, what all this shows is that Postulates 1 through 5 may be viewed as grounding a number of techniques for the comparison of angles. And so in much the same way that Postulates 1 through 3—that is, the existence of lines and circles—serve the purpose of grounding the possibility of comparisons of length, so too these postulates along with the postulates stating the equality of right angles and the existence and uniqueness of parallels serve the purpose of grounding various methods of angle comparison. However, the so-called principle of superposition must also be acknowledged as playing an important (though underappreciated) role here, and it is to this that we now turn.
2.4. The Principle of Superposition and the Comparison of Areas
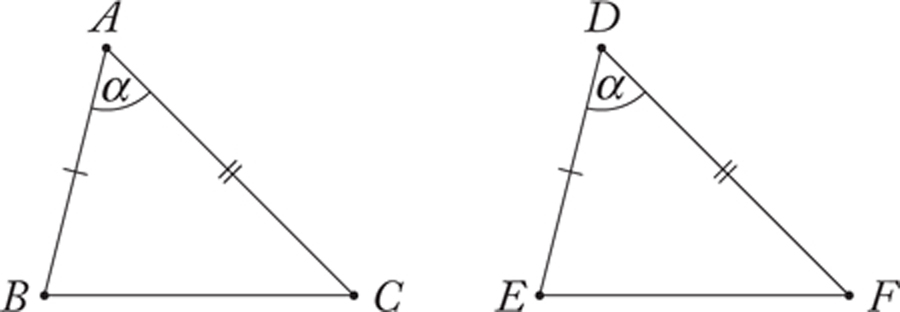
The so-called method of superposition first appears in Book I, Proposition 4. Euclid supposes there that we have two triangles ABC and DEF such that the length of AB is equal to the length of DE, the length of AC is equal to the length of DF, and the angle BAC is equal to the angle EDF:
Euclid’s goal is to prove that the length of BC is equal to the length of EF, and that the remaining corresponding angles are also equal.
Euclid argues that because the length of AB is equal to the length of DE, the length of AC is equal to that of DF, and the angle BAC is equal to the angle EDF, it is possible to superpose the triangle ABC on top of DEF in such a way that A lies on top of D, B lies on top of E, and C lies on top of F.11 If the triangles can be made to coincide in this way, Euclid concludes that in fact all their remaining sides (and angles) must be equal.
How are we to make sense of the ‘superposing’ of one geometric object on top of another in this argument? It is difficult to see any straightforward sense in which Euclid’s postulates justify such a form of argumentation. While this form of argument is not used a great deal in The Elements, the propositions in whose proof it is used—such Book I, Proposition 4—play an indispensible role in the remainder of the text. The net result is that much of the purely geometrical part of The Elements depends in one way or another on this method of proof.
Reactions to the presence of this sort of reasoning in the Elements varies greatly. Russell was famously critical of the method of superposition, saying that ‘it has no logical validity, and strikes every intelligent child as a juggle’ (1938: 405). Others such as Wagner (1983) have been much less hostile. The work of Adams (1994; 2001) carefully discusses a number of historical and conceptual issues that arise with respect to this principle.
There are many complicated issues surrounding this principle, and it is not my goal to discuss them in depth here. My view is that although this principle is not entailed by Euclid’s postulates, it is nevertheless a reasonable principle of geometrical reasoning. I do not know why Euclid did not include some version or other of this principle as a postulate, and will not try to speculate on the matter. Instead, I confine myself to a few remarks on the character and role of this principle in The Elements as it bears on the issues of this paper.
One reason people like Russell have balked at Euclid’s use of the principle of superposition is that, insofar as it is a method that involves moving one geometric object on top of another, it involves the concept of motion. But we have been given no postulates about motions, and Euclid proves no theorems about motions in the Elements. Thus the use of motion in proofs such as that of Book I, Proposition 4 seems conceptually out of place.
However, I do not think that there is any reason to think of the principle of superposition as involving any sort of motion. Rather, it is a principle which says, loosely speaking, that two geometrical objects which agree in sufficiently many respects will agree in all intrinsic respects. For example, in the case of triangles, one has the following principle:
Superposition principle for triangles: Let ABC and DEF be triangles such that AB and DE are equal in length, AC and DF are equal in length, and angle BAC is equal to angle EDF. Then triangles ABC and DEF agree in all their intrinsic geometric properties.
A principle of this sort is enough to prove Proposition 4 of Book I, as we can conclude from the superposition principle that, for example, BC and EF are equal in length. Now, the formulation of a very general principle of superposition applying to a very general class of geometrical objects is a non-trivial task, and so we do not attempt to formulate a fully general principle of superposition here. The important point is simply that whether formulated in a very general way or not, a principle of this sort that says that under certain conditions two geometric objects share all their intrinsic properties does not involve the concept of motion in any way.
It is worth noting that in his formulation of the postulates of geometry in Hilbert (1902), Hilbert has a postulate (Postulate IV, 6) with this rough character, as do Avigad, Dean, and Mumma (2009) in their logical formalization of The Elements. So the idea that we should think of superposition in these terms rather than in terms of motions is not new. It is in these terms that I will think of the principle of superposition in what follows.
As a tool for comparing quantities in The Elements, the principle of superposition plays two roles that we shall now discuss. First, the principle is explicit in the first method of comparison of angles discussed in the previous section. In this method, the equality or inequality of two angles ABC and DEF is reduced to the equality or inequality of the lengths A’C’ and D’F’ of the bases of isosceles triangles having angles ABC and DEF respectively at their vertices, with all other side lengths equal. This method critically depends on the principle of superposition—without it, we could not, for example, conclude that if A’C’ and D’F’ are equal in length, then angles ABC and DEF are equal in magnitude.12
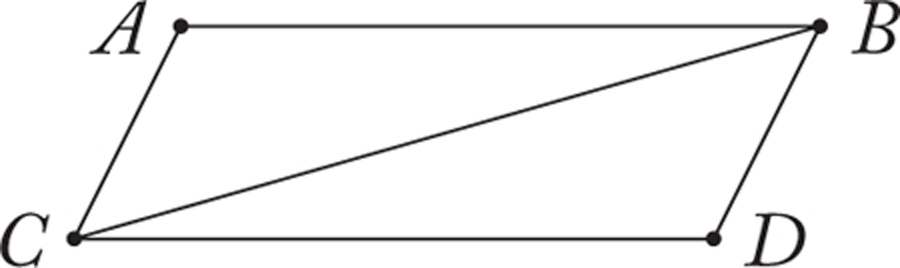
Second, it may be argued that in The Elements the principle of superposition plays a role in the comparison of areas. Euclid’s first theorem about areas is Proposition 34 of Book I, in which he argues (amongst other things) that the diameter of a parallelogram bisects its area. That is, given a parallelogram ABCD:
the areas of triangles ABC and BCD are equal. Euclid proves this by arguing that the respective sides and angles of triangles ABC and BCD are all equal. From this he concludes without further argument that the areas of these triangles must also be the same. But why is this step justified? If we think of the area of a triangle as an intrinsic geometric property of the triangle, then it seems that Euclid must be assuming something like the superposition principle for triangles. Without such an assumption, we would have no right to infer the equality of triangles ABC and BCD. Indeed, essentially all of Euclid’s theorems about areas in The Elements depend on precisely this form of argument in one way or another.
Thus, it can be argued that the principle of superposition (as thus stated) is the main tool for the comparison of areas in The Elements. It must immediately be conceded that there is something speculative about this claim. Euclid does not indicate when he is using the principle of superposition; in fact, he does not explicitly outline or reference any such principle anywhere in The Elements. The principle is rather one which interpreters have brought to The Elements to make sense of its underlying logic—especially the logic of proofs such as that given for Book I Proposition 4. I think that interpreters have been right to do this, but that they have been remiss in leaving the question of the logic of Euclid’s arguments for the equality of areas untouched. Insofar as there is a formulation of the principle of superposition which can serve both roles and could plausibly have been regarded as obvious to Euclid, it makes sense to interpret the principle in that manner. Thus formulated, the principle of superposition may therefore be regarded as a prerequisite not just for certain methods of angle comparison, but also as a prerequisite for Euclid’s methods for the comparison of areas.
2.5. A Conjecture
At this point, I would like to make a conjecture about Euclid’s reason for choosing his five postulates.
The science of metrology is the study of how we measure things, what sorts of measuring instruments may be used for what purposes, and related concerns. The Ancient Greeks even before Euclid were presumably in possession of such a science. There is no reason to think that possession of this science requires the co-existence of a particularly rich idea of mathematical proof. One could potentially develop quite sophisticated tools for measuring areas, volumes, and angles without the idea that associated mathematical generalizations were capable of proof. One could instead develop such a set of tools and techniques proceeding instead with mostly empirical knowledge of the sorts of relationships that hold between numbers, various geometric objects, and so on.
Even absent a rich notion of mathematical proof, one may nevertheless see certain principles as playing a foundational role in metrology, acting as the grounds on which certain fundamental techniques of measurement may be based. I have argued that Euclid’s postulates can be seen as such foundational principles. Indeed, my conjecture is that Euclid chose his five postulates (and perhaps the principle of superposition should be added here) precisely because of their role as foundational principles in the science of metrology; that is to say, precisely because they are basic principles that allow one to compare lengths, angles and areas. Euclid of course did not explicitly give any reasons for choosing his postulates, and so my claim here is highly conjectural. Nevertheless, some support for this conjecture is found in the fact that, as shown in the previous sections, Euclid’s actual techniques for comparing lengths, angles and areas in The Elements all depend on his five postulates (and the principle of superposition) in very direct ways. That Euclid uses his postulates as tools to aid in comparisons is something we find in the text; what goes beyond the text is the conjecture that it is simply with this use in mind that these postulates are chosen. Still, the conjecture seems plausible and so I make it.
Euclid’s choice of his postulates should not be seen as the clever identification of a set of indubitable principles to act as the axiomatic basis of geometrical knowledge, allowing the geometer to dispel skeptical worries about the foundations of his subject. In fact, there is no reason to think that in Euclid’s time there was any sort of skepticism about geometric knowledge that was dispelled by his particular choice of postulates. Nor is there any reason to think that even if there were such worries, Euclid’s particular choice of postulates would have dispelled them. Rather, Euclid’s goal (I conjecture) was to show that beginning with ordinary suppositions that would have been taken for granted by any sort of scientist in possession of at least a primitive science of metrology, one could in fact prove a large set of generalizations about geometrical objects. There is more to be said about this last part of the story, and so it is time to turn to it; with its help we will be able to bring into relief not only the conjecture of this section, but further conjectures still.
3. Comparing the General
3.1. General Measurements
Thus far, we have been talking about measurements of particular geometrical objects—more specifically, judgments in which two physically given and completely determinate lengths, angles or areas are compared. Although the ability to make such judgments is crucial for the possibility of geometry, understanding the nature of these judgments is not Euclid’s goal. Nevertheless, some reflection on the kinds of theorems that actually appear in The Elements shows that the conceptual distance between these sorts of measurements and the kinds of things with which Euclid is actually concerned is perhaps smaller than one might think.
Consider the fact that the sum of the angles in a triangle is 180°. In Euclid’s language, this claim is stated as ‘the sum of the three interior angles of the triangle equals two right angles’, and is part of Book I, Proposition 32. Now, the judgment that for some specific, physically given triangle and some specific, physically given straight angle (or pair of right angles) the sum of the angles in the former is equal to the later is the kind of thing that can be established by the methods of measurement discussed already. Call this a specific measurement. In a specific measurement, two physically given and completely determinate objects are being compared in some way or another.
But establishing that the sum of the angles in a specific triangle is equal to some specific pair of right angles by some sort of specific measurement is not Euclid’s goal in Book I, Proposition 32. His concern instead lies with triangles in general. We interpret this sort of generality in the following way. In the case of a specific measurement, one is interested in a comparison between two completely specified, physically given, and fully determinate objects. What Euclid wants to do, however, is compare two geometrical objects which are only partially specified; namely, the sum of the angles in an arbitrary triangle (with any angles and side lengths, located anywhere in space), and an arbitrary pair of right angles. We do not know anything about the triangle and right angles in question other than that they are triangles and right angles, and in this sense they are only ‘partially specified’ geometrical objects. We think of a comparison between partially specified geometrical objects as in effect infinitely many comparisons between fully specified, physically given and completely determinate geometrical objects compatible with the specification in question. Call this sort of comparison of only partially specified geometrical objects a general measurement.
There is no a priori reason to expect that general measurements should be possible. In some cases, a general measurement will be impossible because the result of the relevant comparison is simply indeterminate. For example, is an arbitrary angle greater than an arbitrary right angle? Here, no general answer is possible—it might be greater, and it might not. In such a case, there is no possibility of a general measurement insofar as we demand that general measurements yield determinate results.
But even in cases in which there is a completely determinate answer to the question of the relationship between two partially given geometrical objects—as occurs, for example, when comparing the sum of the angles of a triangle with two right angles—it might still not be clear how exactly one is supposed to measure something general—that is to say, how to do what amounts to infinitely many specific measurements at once. Certainly, traditional instruments of measurement can offer no help. We cannot, after all, apply a straightedge or compass to a general triangle, but only to a particular one.
The key, however, is to note that the postulates that underlie the possibility of specific measurement—i.e., Euclid’s five postulates along with the principle of superposition—are already claims of a general nature. It will be precisely because of this that general measurements turn out to be possible. Let us consider some examples and see how this works.
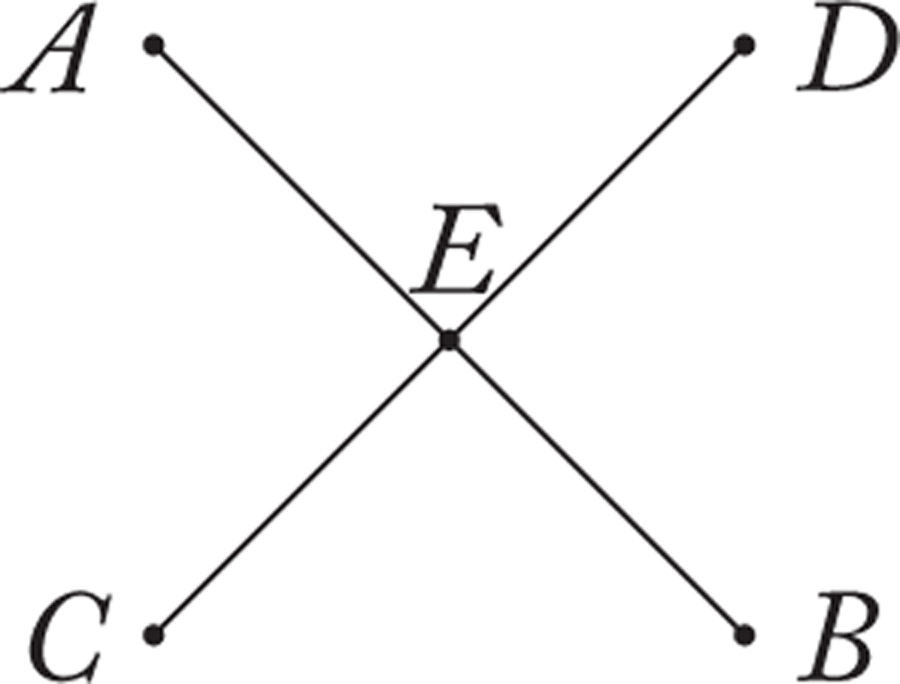
First consider the simple fact that when two lines cross each other, the opposite angles are equal. In terms of the figure above, this means that angles CEA and DEB are equal. This is proved in Book I, Proposition 15. The argument is simple, and we have seen it already. The sum of angles CEA and AED is two right angles, as is the sum of angles AED and DEB. Because all right angles are equal to each other, it follows that the sum of angles CEA and AED is equal to the sum of angles AED and DEB. Eliminating the common element AED, it follows (using the common notions) that angles CEA and DEB are equal.
In this case, it is the generality of the fact that all right angles are equal (Euclid’s Postulate 4) that allows us to compare two opposite angles in the general case in which two lines intersect. In this way, a general measurement involving only a partially specified geometrical configuration is possible.
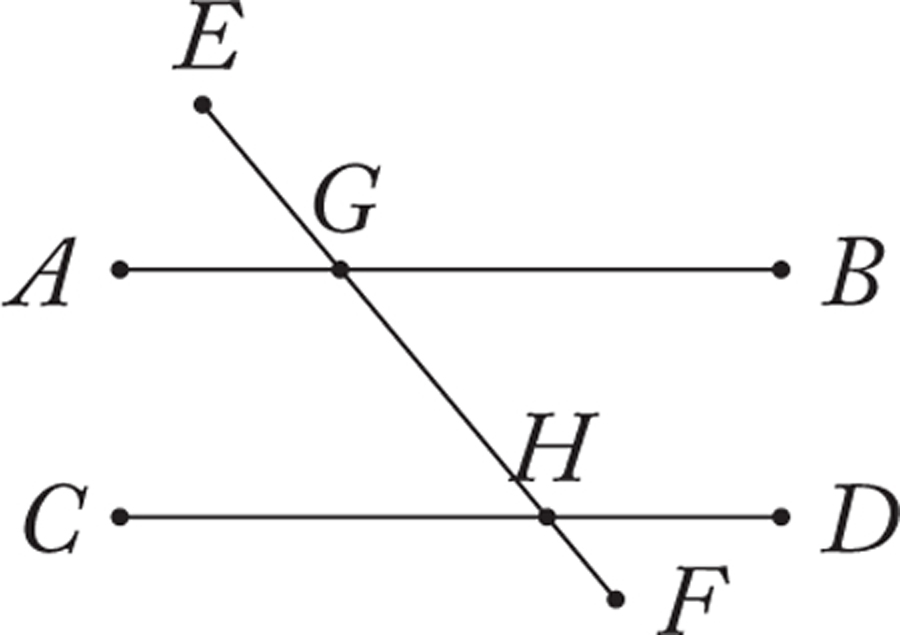
Consider next the fact that when a line crosses two parallel lines, alternate and corresponding angles are equal. In terms of the figure above, this means for example that angles AGH and GHD and CHF are all equal. This is part of the content of Book I, Proposition 29. The argument resembles one we have seen already. If angles AGH and CHF are unequal, then one is greater; suppose it is AGH. With a little work, one then argues that the sum of angles BGH and GHD is less than two right angles. But from Euclid’s Postulate 5, it then follows that the lines through AB and CD meet, and so are not parallel. Thus, angles AGH and CHF cannot be unequal, and so are equal. Because angles GHD and CHF are opposite angles it follows from the previous theorem that they too are equal, and thus all of angles AGH, GHD and CHF are equal. In this case too, it is the generality of Euclid’s postulates—and in particular, the generality of Postulate 5—that allows us to make a general comparison between angles in a geometrical configuration that is only partially specified.
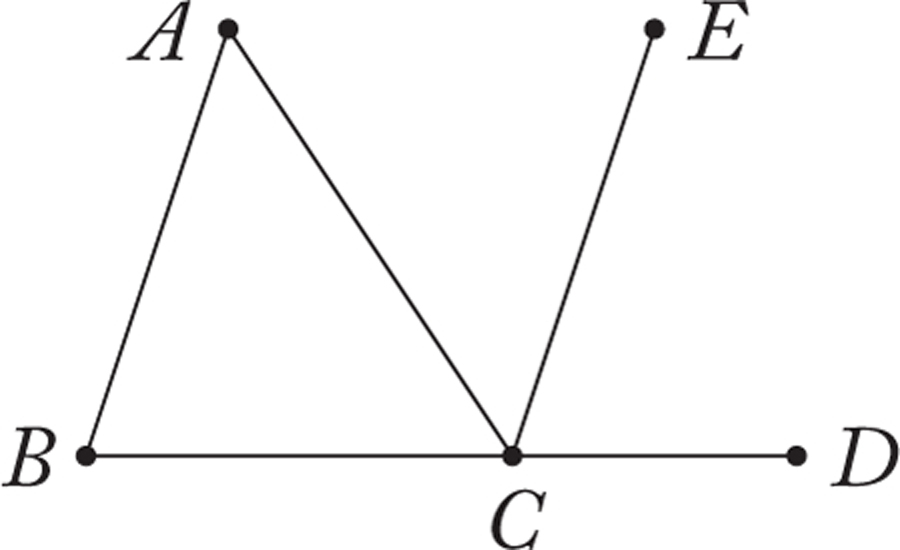
Finally, we consider the fact that the sum of the angles in a triangle is equal to two right angles. Consider the triangle ABC given above. Extend line segment BC through C to a point D, and draw a line CE parallel to BA. Angles ABC and ECD are corresponding angles, and so are equal by the theorem just proved. Angles CAB and ACE are alternate angles, and so are also equal by the theorem just proved. Therefore the sum of the angles ABC, BCA and CAB is equal to the sum of the angles ECD, BCA and ACE, which is equal to two right angles.
What we have here is a more complex general measurement that builds on simpler general measurements to demonstrate a relationship of equality. In this case, it is the generality of the simpler general measurements that make possible the generality of the more complex general measurement of the sum of the angles of an arbitrary triangle.
In sum, the principles of specific measurement themselves already contain sufficient generality to serve as the basis for general measurement. In this way, the gap between specific and general measurement turns out to be quite small; the theoretical basis of the former sufficing to ground the later. Recognizing this is perhaps the crowning accomplishment of Euclid and his contemporaries.
3.2. The Structure of The Elements
It is not just the theorems described above that may be interpreted as general measurements. In fact, a great number of the propositions of Books 1 through 4 of The Elements may be interpreted straightforwardly as general measurements— that is, as arguments showing that in a certain partially specified geometrical configuration, certain lengths, angles or areas are less than, equal to, or greater than certain other lengths, angles or areas. For example, Pythagoras’s Theorem (in the way stated in Book 1 Proposition 47) may be viewed as a general measurement comparing the sum of the areas of the squares on the legs of a right angled triangle with the area of the square on the hypotenuse.
Although many of the propositions of The Elements are straightforward geometrical facts for which proofs are then given, The Elements also contains a good number of constructions—that is, propositions of the form ‘given such-and-such, to construct such-and-such’. So for example, Proposition 1 of Book 1 reads ‘to construct an equilateral triangle on a given finite straight line.’ In the case of constructions, Euclid not only gives the method for constructing the object in question, but also a proof that the construction does indeed do the job it is supposed to do. In such cases, one even has the option of viewing the proof as a general measurement. So for example, in the case of Proposition 1 of Book 1, the claim is that when a triangle is constructed in a given way, all the sides are of equal length. This may be viewed as a general measurement in which the sides of a triangle constructed in a particular way are compared with each other. A great number of the constructions of Books 1 through 4 can be interpreted in a similar way. Of course, it might be a stretch to claim that all the theorems of Books 1 through 4 are naturally viewed as general measurements. For example, to interpret the constructibility of the general pentagon as a general measurement would (perhaps) be a stretch. But this I think does not refute the idea that the development of increasingly sophisticated general measurements is one of the central goals of Books 1 through 4.
Although my main claim concerns the propositions of Books 1 through 4 of The Elements, a few comments on the remaining books will be helpful, at least to make clear what makes Books 1 through 4 distinctive. The subject of Book 5 is the theory of proportions (or ratios); the subject matter here is more algebraic than geometric, and so is not our primary concern. In Book 6, however, the theory of proportions is then put to use in geometry. Consider, for example:
Proposition 1, Book 6: Triangles and parallelograms which are under the same height are to one another as their bases.
This says, for example, that if two triangles have the same height, then the ratio of their areas is the same as the ratio of their bases. This is first and foremost a statement about equality between ratios of areas of lengths, rather than a statement about equality of lengths or areas per se. Can we think of this result as a general measurement? The most natural way to do so is to expand our notion of measurement to include not just claims about equalities or inequalities between lengths, angles and areas, but also claims about equalities or inequalities between ratios of such quantities. Taking this approach, many of the results of Book 6 may also be viewed as general measurements.
Books 7 through 9 of The Elements concern number theory. While some have suggested that Euclid is here ‘geometrizing’ number theory—that is, subsuming number theory under geometry—there is very little textual or mathematical basis for this claim. The theorems in these books do not, for example, depend on Euclid’s original postulates in any non-trivial way, and in fact end up invoking other principles, such as that of mathematical induction. The focus of this paper being geometry, we do not attempt to analyse Euclid’s conception of number theoretic proof here.13
Book 10 concerns the theory of incommensurability. There is both a geometric and a number theoretic character to the results presented there. Nevertheless, the theory of commensurability is only geometric in a superficial way, as Euclid’s original five postulates are also rarely invoked in Book 10. Given that the motivation for a theory of incommensurability and the character of such a theory are very different from that of the more purely geometrical theory developed in the earlier books of The Elements, we do not attempt to subsume Book 10 under the way of thinking about geometric proof being developed here.14
In Books 11 through 13 of The Elements there is a return to more purely geometrical matters, though with a focus on solid (as opposed to plane) geometry. There is much in these chapters that can be interpreted as a theory of general measurements in three dimensions. Nevertheless, there are important differences between the results of these books and the results of earlier books, even beyond the move from two to three dimensions. Consider for example the method of exhaustion, which is developed in Book 12 and is used to derive facts about the areas of circles and other figures by approximating them with polygons. This method invokes surprisingly sophisticated notions of convergence, and presupposes much more than the five postulates of Book 1. In these later books, we see a transition to a more sophisticated, ‘higher’ mathematics, and so the character of many of the proofs there differ in important ways from those of the earlier books of The Elements.
In sum, given our interest in the origins and nature of geometrical proof and the role that Euclid’s five postulates play therein, we focus on the results of Books 1 through 4, though much of our argument can be generalized to cover up through Book 6, and occasional proofs in later books.
3.3. Proofs of General Measurements
Before returning to the general questions with which we began this paper, I will point out a further important way in which the proofs contained in (at least) the first 4 books of The Elements may be interpreted as general measurements.
In the propositions of first 4 books of The Elements, a geometric object is given or constructed, and some relationship of equality or inequality between lengths, angles or areas is stated and then proved. (In the case of book 6, it is some sort of equality or inequality of proportions that needs to be shown, but we focus on the simpler case of the first 4 books.) In the process of proving the result in question, additional lines or circles are often added to the original figure. I claim that these additional lines or circles always serve the purpose of allowing the kinds of comparisons between lengths, angles or areas discussed in §2.
It will be easiest to illustrate this by means of an example. Consider again the proposition that the sum of the angles of a triangle add up to 180°. We have already seen the diagram that accompanies the proof:
Here, in addition to the triangle ABC which is given, two lines are added—BC is extended to BD, and a line CE parallel to BA is drawn. These lines are added precisely in order to allow a comparison between angles BAC and ACE, and angles ABC and ECD, using the kind of reasoning presented in §2. This then allows us to compare the sum of the angles of the triangle with the straight angle BCD. In this way, the addition of lines to the original triangle allows us to reduce the comparison of the sum of the angles of the triangle with two right angles to the much simpler problems of the comparison of angles BAC and ACE, and angles ABC and ECD, which in turn can be performed using the methods of §2.
In fact, Euclid’s general proof-strategy for general measurements is to add lines and circles to a given geometrical configuration in such a way that a general measurement can be reduced to simpler general measurerements. In this way, general measurements can ultimately be reduced to the kind of canonical general measurements implicit in §2. In much the same way that imposing a grid over an object allows us to approximately measure the dimensions of an object, the careful addition of lines and circles is what allows Euclid to perform general measurements of complex geometrical configurations.
In the case of Euclid’s constructions—i.e., propositions in which given some geometrical configuration, some other geometrical configuration must be constructed—typically the various circles and lines involved in the construction itself will be sufficient to then argue that the relevant equalities or inequalities hold between the lines, angles or areas constructed.
Note that in saying that Euclid reduces general measurements to the kind of canonical general measurements implicit in §2, I am not claiming that Euclid reduces general measurements to specific measurements. There are, after all, no specific measurements anywhere in The Elements—Euclid’s geometric claims are always general in nature. The point to be reminded of here is that even the basic postulates underlying the science of specific measurements are of a general nature, and can thus be applied to geometrical configurations that are not fully determinate. In this way, in appropriate situations the techniques for comparison introduced in §2 yield general measurements.
4. On The Nature of Proof In Euclid
4.1. General Reflections
At this point, the ingredients for the story I wish to tell about Euclid’s conception of mathematical proof are all in place. In fact, the story itself should already largely be clear.
I begin with the assumption that the ancient Greeks not only had a wide range of techniques for comparing specific lengths, angles and areas, but also a science of specific measurement, in the sense discussed in §2.5. In particular, I suppose that the Greeks had some sort of understanding of the basic principles that make such techniques of measurement possible in the first place. These principles, I have argued in section §2, can be grounded in Euclid’s five Postulates.
My next main conjecture is that armed with these postulates, Euclid realized that not only can techniques of specific measurement be grounded, but also more general comparisons of lengths, angles, and areas between geometric objects that are only partially specified—I have called these comparisons general measurements. These comparisons are done not with ruler and compass or other instruments, but by reasoning with the basic principles of specific measurement.
It is in this transition from a science of specific measurement to a science of general measurement that the notion of (geometric) proof emerges. Specific measurements are primarily done with measuring instruments, though a genuine science of specific measurement also requires some basic reasoning with the principles that make specific measurement possible in the first place. With general measurement, however, measuring instruments are of no use because the geometric object is never fully given. One cannot apply a straightedge or compass to a general triangle; one can only apply such instruments to a completely determinate and given triangle. Thus, in general measurement the only tool at one’s disposal is reasoning with basic principles. It is not obvious that this will be enough; but the genius of Euclid and his contemporaries lay in recognizing that armed only with this much, a rich theory of general measurement is in fact possible.
In this way, my suggestion is that a large part of The Elements should be viewed as a series of increasingly sophisticated general measurements. Just as one can imagine an increasingly sophisticated series of specific measurements, beginning with measurements of ordinary objects at hand and culminating with the measurement of the height of a distant mountain, the circumference of the earth, or the distance to the moon, so too we should think of The Elements as an increasingly sophisticated series of general measurements starting with simple comparisons and culminating in such things as the comparison of the area of a square on the hypotenuse of a right angled triangle with the areas of the squares on its legs.
On this reading, one of the main motivations behind The Elements is not that of trying to establish geometrical knowledge with some sort of certainty, but rather the developing of increasingly sophisticated techniques for general measurement. Insofar as we think of the modern notion of mathematical proof as directed towards the production of certainty—perhaps certainty that given propositions follow from given postulates—it is not even clear that the best way to think of Euclid’s arguments in The Elements is as instances of proofs in the modern sense. Instead, it seems to me better to think of proof in much of The Elements as the tool with which we perform general measurement. Perhaps it will need to be conceded that in the later books of The Elements the notion of proof becomes more sophisticated, but we will not examine that matter here.
Let us then return to the questions with which we began the paper, though their answers too should largely be clear by now. Our first question was how we should view the status of Euclid’s postulates, and in particular, the five postulates with which The Elements begins. As I have argued, these are basic principles that ground our ordinary techniques for specific measurement. In this capacity, they are not supposed to be self-evident, or even the ‘most familiar’ of principles. They are rather something like conditions for the possibility of specific measurement in the ordinary way in which specific measurements are actually performed.
The next question we posed was why Euclid did not treat lengths, angles and areas as intrinsically associated with real numbers. My answer is that to associate real numbers with lengths, angles and areas is to presuppose that it makes sense to talk about one length, angle, or area as having a definite mathematical relationship to another length, angle or area (such as being equal to, less than, greater than, twice as large as, and so on.) It is part of the job of a science of measurement, however, to justify the claim that such relationships hold in any specific or general setting. As a textbook in the science of measurement, Euclid therefore deliberately refrains from supposing that lengths, angles and areas can be intrinsically measured, instead showing how such comparisons are possible in the first place. Of course, having shown how lengths, angles and areas can be individually compared does not get one all the way to associating such magnitudes with numbers. But it is a necessary step along the way. A more modern account of the notion of real number—one that perhaps tackles the problems of incommesurables—is necessary to close the gap. But that does not contradict the fact that it is out of a need to justify the association of numbers with physical magnitudes that Euclid refrains from doing so. It is therefore not because of a lack of imagination or lack of mathematical technique that Euclid presents his material the way he does, but rather because of the very character of the project in which The Elements is engaged.
4.2. Two Remarks
Although my main argument is complete, a final pair of more tangential remarks will also shed some further light on the issues just raised.
First, it is sometimes suggested that the purely geometrical books of the The Elements should be viewed as textbooks in the art of ruler and (collapsible) compass constructions. It is often said that ruler and collapsible compass constructions played a special role in Greek mathematical culture, and that The Elements is a systematic exploration of what can be done with these tools.15 It is sometimes even suggested that ruler and compass constructions were regarded as the most pure of geometric constructions, or perhaps even had a special religious significance (Seidenberg 1962), and that it was because of this that Greek mathematicians were especially concerned with what could and could not be done with such tools.
There is however very little textual support for the idea that the Greeks around the time of Euclid thought there was something antecedently special about ruler and compass constructions, and that The Elements was some sort of expression of this fact. Euclid certainly does not mention any such thing explicitly. Plato mentions the beauty of ruler and compass constructions in the Philebus, (e.g., 51c, 56c), but other than that there is no mention of ruler and compass constructions in his entire corpus, and what we find here in the Philebus is surely not enough on which to base a case for this sort of interpretation of The Elements. Nor do we find any such support in Aristotle, or in any text roughly contemporaneous with Euclid.16 Moreover, the use of other tools (such as a marked ruler) in the works of Pappus, Appolonius and Archimedes does not seem to have caused any concern that has been recorded.17 Indeed is not until significantly later in antiquity that one finds sustained and fully explicit discussions of ruler and compass constructions. While the mathematicians of antiquity seemed to have preferred ruler and compass constructions when available, nothing more can be inferred from this than a preference for mathematical simplicity.
My suggestion then is that we view The Elements first and foremost as a text in the science of general measurements. Now, insofar as all the constructions in The Elements can be done with ruler and compass, there is a sense in which the The Elements shows us that there is something special about ruler and compass constructions. After all, we have seen in §2 that ruler and compass constructions suffice for the comparison of any two specific lines or angles. That ruler and compass constructions play a special role in the theory of measurement does not entail, however, that it is out of a desire to understand how much can be done with ruler and compass that The Elements was written. To the contrary, my conjecture is that it is out of a desire to understand the possible range of general measurements that The Elements was written, and that ruler and compass just so happen to be sufficient to do everything contained therein.
The second more tangential remark I wish to make concerns the comparison of line segments, and is an issue raised in §2 whose discussion I have deferred until now. Perhaps the most natural method for comparing line segments would be to bring a ruler to one line segment, mark the ends, then bring the ruler to the other line segment and simply compare them. This is what elementary school students are taught to do. Any science of measurement would surely need to include methods of this sort. Yet Euclid opts to base his general measurements on more complicated ways of comparing line segments, such as the straightedge and compass method outlined in §2. Why does he do this, and what are we to make of it?
It is certainly possible to theorize abstractly about the elementary school method of line comparison just described and build a theory of general measurement around it. Perhaps the most well known approach in this rough direction is that of Klein (1893). Klein took the notion of a symmetry (or rigid transformation) of space as fundamental. Klein then used the (continuous) group of symmetries of that space as a way of defining congruence of geometrical objects, by saying that two objects are congruent iff there is a rigid transformation taking one to the other. Using this basic idea, Klein then reduced the study of the geometry of space to a study of the properties of the group of symmetries of that space. If we think of the dragging of a ruler through space as just a continuous sequence of rigid transformations, Klein’s way of doing geometry can be thought of as based on the principles underlying a set of methods of specific measurement, where these methods of specific measurement now include the elementary school method of line comparison (perhaps amongst other methods). Although much can be said about the details of Klein’s approach, this broad outline will suffice for now.
What the work of Klein reinforces is that when someone like Euclid or Klein grounds geometry on the principles underlying various methods of specific measurement, there is no attempt to incorporate the principles underlying every possible method of measurement. Instead, a choice is being made as to which methods of measurement to interrogate. Some of these choices will be more fruitful than others. For Euclid, Klein’s choice was not an option, requiring as it does relatively complicated mathematics, even in the simplest case. Part of the genius of Euclid and his contemporaries lay in choosing a set of techniques of specific measurement whose underlying principles could be used to generate a rich theory of geometry using only fairly elementary argumentation. This aspect of their mathematical genius has, I think, been underappreciated.
Acknowledgements
I am very grateful for discussions with Tom Pashby, Ermioni Prokopaki, Daniel Sutherland and Anubav Vasudevan about the topics of this paper.
Notes
- I work throughout with Heath’s translations, as presented in Heath (1908). ⮭
- For an excellent discussion of deduction in Greek mathematics, see Netz (1999). ⮭
- This is a point Meuller makes in a different context; see Mueller (1969: 294). ⮭
- The claim that in The Elements two figures have the same area in case one can be decomposed and re-assembled into the other is, while not entirely untrue, nevertheless perhaps an over-simplification. Often, Euclid shows that two figures A and B have equal areas by showing that for some other figure C disjoint from A and B, the larger figure A ⋃ C can be decomposed and re-assembled in to B ⋃ C. Additional problems and questions about the nature of areas are also raised by the later books of the Elements. However, the topic of the concept of area as it appears in The Elements, well deserving of a treatment all its own, is not our main concern and so we do not pursue these matters further here. ⮭
- The general point being made here is similar to one of the main points of Seidenberg (1978). ⮭
- There is a further question as to whether Greek views on incommensurables also contributed to the rejection of an a priori identification of lengths, angles, and areas with numbers. A discussion of the views of ancient Greek mathematicians on incommensurables unfortunately lies outside the scope of this paper. It will suffice to note, however, that it is possible for the rejection of an a priori identification of geometrical magnitudes with numbers to have multiple causes. ⮭
- The reasoning here relies on Euclid’s common notions. ⮭
- This is only intended to be a way of comparing angles not greater than 180° in magnitude. ⮭
- By a line parallel to a given line we mean a line which, regardless how far it is extended, does not meet the given line. ⮭
- Concerning this postulate, note that Heath says, ‘this postulate … really serves as an invariable standard by which other (acute and obtuse) angles may be measured… ‘ (1908: Vol. 1, 200). I take this to be consistent with the reading I am offering here. See also Heath (1908: Vol. 1, 201) for other historical examples of this way of treating Postulate 4: ‘Veronese, Ingrami, and Enriques and Amaldi deduce the fact that all right angles are equal from the equivalent fact that all flat angles are equal, which is either itself assumed as a postulate or immediately deduced from some other postulate.’ ⮭
- Perhaps the reasoning is that because AB and DE are equal in length, we should be able to slide the triangle ABC over in such a way that A is laid on top of D and B on top of E. Assuming the triangles are oriented similarly, then because angles BAC and EDF are equal, D (which now co-incides with the newly moved A) and F should lie in the same line as the newly moved C. Because AC and DF are equal in length, it then follows that F and the newly moved C should in fact co-incide. ⮭
- In this regard, it is worth noting that in proving Propositions 24 and 25 in Book I—propositions which in effect justify the method of angle comparison in question—Euclid relies on propositions proved using of the principle of superposition, such as Proposition 4 of Book I. ⮭
- For a rich discussion of Euclid’s approach to number theory, see Mueller (1981). ⮭
- For a thorough discussion of the Greek theory of incommensurability, see Knorr (1975). ⮭
- One finds this idea, for example in Mueller (1981: 16):
However, one also finds voices of dissent. For example, see Heath (1908: Vol. 1, 124):The demonstration that a whole series of constructions can be carried out with straightedge and compass is clearly one of the purposes of the early books of the Elements. Why Euclid chose precisely these means does not seem to be directly ascertainable.
⮭There is of course no foundation for the idea, which has found its way into many textbooks, that “the object of the postulates is to declare that the only instruments the use of which is permitted in geometry are the rule and compass.”
- The availability of searchable versions of a large number of texts of antiquity makes it relatively easy to establish this. ⮭
- For a mathematical and historical discussion of the marked ruler, see Martin (1998: Ch. 9). ⮭
References
Adams, Ernest (1994). On the Method of Superposition. British Journal for the Philosophy of Science, 45(2), 693–708.
Adams, Ernest (2001). Surfaces and Superposition. CSLI Publications.
Avigad, Jeremy, Edward Dean, and John Mumma (2009). A Formal System for Euclid’S Elements. The Review of Symbolic Logic, 2(4), 700–768.
Burton, Harry (1945). The Optics of Euclid. Journal of the Optical Society of America, 35(5), 357–72.
Feferman, Solomon (2000). Does Mathematics Need New Axioms? Bulletin of Symbolic Logic, 6(4), 401–46.
Heath, Thomas (1908). The Thirteen Books of the Elements (Vols. 1–3, 2nd ed.). Cambridge University Press.
Hilbert, David (1902). The Foundations of Geometry. The Open Court Publishing Company.
Kangshen, Shen, John Crossley, and Anthony Lun (1999). Nine Chapters on the Mathematical Art. Oxford University Press.
Klein, Felix (1893). A Comparative Review of Recent Researches in Geometry. Bulletin of the New York Mathematical Society, 2(10), 215–49.
Kline, Morris (1972). Mathematical Thought from Ancient to Modern Times (Vol. 1). Oxford University Press.
Knorr, Wilbur (1975). The Evolution of the Euclidean Elements. Springer Netherlands.
Martin, George (1998). Geometric Constructions. Springer-Verlag.
Mueller, Ian (1969). Euclid’s Elements and the Axiomatic Method. The British Journal for the Philosophy of Science, 20(4), 289–309.
Mueller, Ian (1981). Philosophy of Mathematics and Deductive Structure in Euclid’s Elements. The MIT Press.
Netz, Reviel (1999). The Shaping of Deduction in Greek Mathematics: A Study in Cognitive History. Ideas in Context. Cambridge University Press.
Russell, Bertrand (1938). The Principles of Mathematics (2nd ed.). Cambridge University Press.
Seidenberg, Abraham (1962). The Ritual Origin of Geometry. Archive for History of Exact Sciences, 1(5), 488–527.
Seidenberg, Abraham (1978). The Origin of Mathematics. Archive for History of Exact Sciences, 18(4), 301–42.
Wagner, Robert (1983). Euclid’s Intended Interpretation of Superposition. Historia Mathematica, 10(1), 63–70.