On Mereology and Metricality

Zee R Perry; Z. R. Perry

doi:10.3998/phimp.4121

We represent physical quantities, in science and our everyday practice, using mathematical entities like numbers and vectors.^¹ We use a real number and unit to refer to determinate magnitudes of mass or length (like 2kg, 7.5m etc.), and then appeal to the arithmetical relations between those numbers to explain certain physical facts. I cannot reach the iced coffee on the table because the shortest path between it and me is 3ft long, while my arm is only 2.2ft long, and 2.2 < 3. The scale at the farmer’s market does not tilt because one pan holds a 90g tomato while the other holds two strawberries, of 38g and 52g respectively, and 38 + 52 = 90. The amount of water that spills out of the tub when Archimedes gets in is 3.5-times greater than what spills out when Archimedes Jr. gets in, because their bodies’ volumes are 83.3 and 23.8 cubic decimeters, respectively, and the ratio between 83.3 and 23.8 is 3.5 : 1 (i.e. 83.3 = 3.5 * 23.8).

It seems right to say that, while they provide a convenient way to express these explanations, the mathematical ‘<‘ relation, or the ‘+’ and ‘*’ operations on the real numbers are not really part of the physical explanations of these events.^² They just represent explanatorily relevant features inherent in the physical systems described—i.e. the features of the tomatoes, strawberries, bathtubs, and ancient Greeks involved. A theory of “quantitative structure” is an account of these features, the physical properties and relations really doing the explaining.

People have thought^³ the proper account of quantities requires that we give up on the idea that quantitative structure be intrinsic in this way. They’ve thought that, to the extent predicates like “2π-times as long as” or “three-and-a-half times the volume of” pick out physical relations at all, they only be defined in terms of global structural characteristics of the domains of lengthy or voluminous entities,^⁴ not in terms of how their relata are in themselves.

I will show that this is a mistake. This paper defends a theory of quantitative structure that does justice to the intuition that the physical relations which constitute quantitative structure are intrinsic. I argue that, for some quantities—namely, the members of a special class of quantities I call “properly extensive”—the explanation for why our mathematical representations are faithful comes from their connection to parthood. Let me give an example of what I mean; consider the following two judgments:

(1) x is shorter than y
(2) x is as long as a part of y

(1) is an instance of an ordering relation on lengthy objects, where the ordering relation is part of what constitutes length’s quantitative structure. (2), alternatively expressed as “some part of y has the same length as x”, can be broken down into, on the one hand, a mereological relation – parthood – and, on the other, the relation denoted by a predicate like “as long as” or “same length as”.^⁵

In this paper, I will argue that claims like (1) reduce to claims like (2).

1. Quantitative Structure is Parthood Structure

More precisely, I defend the Mereological-Reductive (or “M-R”) account of quantitative structure, which defines (1) as “(2) and x and y do not have the same length”, and gives a definition—in terms of parthood and the sharing of determinate length properties—for all the relations which constitute length’s quantitative structure.

Many other accounts of quantitative structure introduce a quantity’s ordering relation, like (1), or summation relation (like what’s appealed to in the balance scale example, or discussed, below, in the case of length) as primitive posits.^⁶ Accounts like these, if they want to capture the intuitive connection between (1) and (2), have to posit bridge laws between their primitive relations and the mereological ones. The M-R account avoids this by taking the connection to be definitional. There is a tradeoff, of course. Primitive posits are as adaptable as their axioms allow them to be, and it’s easy to generalize an account that makes use of, e.g., primitive ordering relations to apply to any quantity that’s ordered. In contrast, the M-R account’s definitions of ordering, summation, and metrical ratio relations can only be satisfied by quantities which put the right necessary constraints on the parthood structure of their instances.^⁷

In this section, I give an overview of the M-R account of quantitative structure, and argue that the commonly accepted way quantitative and mereological structure can be related, what is sometimes called “extensiveness” or “additivity”, is too weak to support this account. The M-R definitions, I argue, apply only to the properly extensive quantities, a special sub-class of the extensive quantities which put additional constraints on the possible mereological structure of their instances.

In sections 3 and 4, I present a formal M-R account of the quantity, volume, which takes its proper extensiveness as fundamental and defines the ordering, summation, and metrical relations which constitute its quantitative structure in terms of this connection to mereology.^⁸ The system also serves as a general schema for M-R accounts of other properly extensive quantities, like length, area, temporal duration, etc. In section 2, I argue that no other theory of quantitative structure does justice to the intrinsicality intuition as it applies to the properly extensive quantities, and present a number of other advantages of the account.

1.1 Summation Structure

If the M-R account is going to be able to do all I’ve promised it can, it needs to give definitions of the ordering, summation, and metrical ratio relations that capture the idea that they reflect something intrinsic to their relata. This is easy in the case of length ordering, since (2) is a natural reading of (1) and is also an intrinsic relation.

It’s less obvious how summation or metrical relations should be defined on this account. A common expression of length summation relations involves talking about length properties rather than lengthy objects. We say “x’s length is the sum of y’s and z’s lengths”. The natural expression of the relation between lengthy objects doesn’t use terms like ‘sum’ at all. Rather, it says

(3) x is as long as y and z put together.

(3) has, if anything, more of a mereological ring to it than (1). Indeed, on a literal reading of ‘put together’, we can gloss (3) as: “x has the same length as an object, o, composed out of y and z put together, would”. However, while this reading is a mereological relation, it will not do as an analysis of (3). This is because it requires appeal to o, and in particular o’s length. But o might not be lengthy; that is, y and z might not be put together in the right way for o to have length (if, e.g., they make a ‘T’ shape). Or o might be lengthy but not have the right length (if y and z have some lengthy overlap, o’s length will not be the “sum” of their lengths).

The M-R account defines summation structure in a different way. It analyzes (3) in terms of y and z’s relations to x’s parts, together with the requirement that those parts are put together “in the right way” (a condition which will vary between different quantities):^⁹

(4) x is composed of a segment as long as y and a segment as long as z, put together in the right way.

Here, the M-R account’s analysis goes beyond the intuitive mereological upshot of the summation relation. The M-R account understands both the ordering and the summation relations as specifying (among other things) something about the physical makeup of one of their relata. To say that b is shorter than a, or to say that a is as long as b and c put together, is to say something about a’s internal structure—specifically, whether a has any parts, what the configuration of those parts is relative to each other, and whether they share length properties with b or c. These relations, so defined, are intrinsic to the system composed by their relata. Indeed, they satisfy a stronger condition: since they depend only on the intrinsic properties of each of their relata—i.e. on how each relatum is in itself —they are not just intrinsic but internal relations.

1.2 Constructing Metric Structure

The M-R account, similarly, defines ratio relations like “twice as long as” or “4.6-times the volume of” in terms of mereological relations and the sharing of intrinsic properties. Though our expressions of them appeal to numerical ratios like 2 : 1 or 4.6 : 1, the physical ratio relations should be understood as relations between concrete physical objects, not as relating objects to numbers. If that’s right, then there are an infinitude of distinct, two-place, ratio relations; i.e. “2-times the volume of” and “4.6-times the volume of” are distinct relations between voluminous objects. The M-R account gives a reductive definition, in terms of mereology and the sharing of intrinsic volume properties, for each such relation, by way of a procedure which pairs ratio relations with their mereological analyses.

Figure 1:

Two voluminous entities.

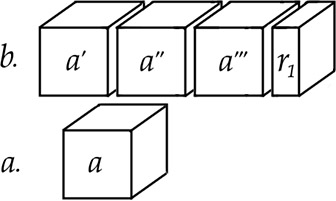
The “ratio procedure”, performed on an ordered pair of voluminous objects, specifies the M-R account’s definition of the ratio relation they stand in. Let me give an example of how this works.^¹⁰ Suppose we want to determine the volume ratio of b to a (how much more voluminous b is than a). We perform the ratio procedure on a and b.

First, we “take a out of b”, where this just means that we partition b into as many non-overlapping copies of a (i.e. parts with the same volume as a) as we can. In this case, that number is 3. Then there is a part of b which is our remainder, r₁, which is smaller than a. For step two, we do the same thing but taking r₁ out of a, which yields 2 non-overlapping copies and another remainder r₂. The third step follows this pattern, taking r₂ out of r₁. r₁ is composed of 2 non-overlapping copies of r₂ with no remainder. Since there’s no remainder, we stop.

This procedure determines the complex mereological property which will be the M-R account’s analysis of the “volume ratio” of b to a (let’s say that b “partitions into” some class of its parts iff no two of the members of that class overlap and b is their fusion):

Figure 2:

Step 1, Taking a out of b.

∃x₁, x₂(b partitions into: 3 parts with the same volume as a, and another part, x₁) ∧ (a partitions into: 2 parts with the same volume as x₁, and another part, x₂) ∧ (x₁ partitions into: 2 parts with the same volume as x₂).

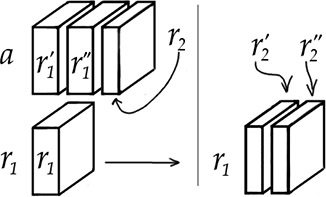
Figure 3:

Step 2 and Step 3

How does this give us the volume ratio between a and b? Taking a out of b tells us approximately how much bigger b is than a. Taking r₁ out of a tells us approximately how much bigger a is than r₁. This, in turn, gives us a better approximation of how much bigger b is than a. Each time we repeat this procedure, we get a better and better approximation. If the procedure terminates, we have a perfect approximation. Indeed, r₂ goes evenly into a and b. From the procedure we can deduce that a is composed of 5 non-overlapping copies of r₂, and b 17 copies. So the ratio of b to a is 17/5, i.e. $b = 175 * a = 3.4 * a$ . Indeed, “b partitions into 17 parts, all with the same volume as r₂, while a partitions into 5 such parts” amounts to the same thing as the definition given above. Why not just use that as the definition for volume ratios, then?

Here’s why: The ratio procedure is not guaranteed to terminate, and if it does not terminate, it cannot output a final remainder (like our r₂). However, there’s another way to determine the ratio between a and b from this procedure that doesn’t require appeal to the final remainder. Recall that the numbers, 〈3, 2, 2〉, output by the procedure, count up certain non-overlapping parts of b, a, and r₁. We can use these to construct what is called a “simple continued fraction”:

175 = 3 + 1 2 + 12

The list of integers output by this procedure is what is sometimes called an “anthyphairetic ratio”.^¹¹ Continued fractions are one way to express this sort of ratio. Even when the ratio procedure does not terminate, it will still output a list of integers that count up the relevant sets of non-overlapping parts of a and b and the various non-final remainders. The only difference is that, when the procedure does not terminate, we get an infinitely long list. This is okay because continued fractions can, in fact, be continued indefinitely, and infinite simple continued fractions also pick out unique real numbers! It’s this formal feature which allows the mereological relations generated by this procedure to serve as the definitions for volume ratio relations.

1.3 Proper Extensiveness

I mentioned before that the M-R account applies only to quantities that put the right constraints on the possible parthood structure of their instances. Here’s what that means: If the M-R definitions of an ordering relation, “LESS-Q”, or summation relation, “Q-SUM”, are to be any good, at the very least the definiens and definiendum must be necessarily coextensive. That is, a quantity, Q, is amenable to the M-R account only if it satisfies:

(5) □(x is LESS-Q than y ↔ x and y have different Q-properties, but x has the same Q property as some part of y)
(6) □(y and z Q-SUM to z ↔ x can be partitioned into two parts that are put together in the right way and which have the same Q-properties as y and z, respectively)

As well as the analogous necessary biconditionals for the ratio relations.

This means that for many (indeed most) quantities, the account cannot get off the ground. An M-R account of temperature, for instance, would get the quantitative relations almost entirely wrong. The ice in the freezer, at 30° Fahrenheit, is less warm than 212°F water boiling on the stove. But this fact about temperature ordering clearly doesn’t mean that the ice in the freezer is as warm as some proper part of the water on the stove!

What about quantities that, unlike temperature, put significant constraints on the mereology of their instances? Additive (also called extensive^¹²) quantities are ones where, intuitively, wholes inherit their Q-properties from the Q-properties of their parts. More precisely, Q is additive just in case: whenever x and y instantiate Q-properties, and are “put together in the right way”, the mereological fusion of x and y instantiates the “sum” of their Q-properties. Being additive is necessary for a quantity to admit of an M-R account of its structure—a quantity is additive just in case it satisfies the right-to-left direction of both (5) and (6)—but it is not sufficient.

Here’s why: Consider the additive quantity, mass. On the standard model of particle physics, there are fundamental particles with different masses, like the electron (approx. 9.19 × 10⁻³¹kg), and the muon (approx. 1.88 × 10⁻²⁸kg). On a straightforward interpretation of this theory, Ellen the electron and Miriam the muon are mereological simples. This is inconsistent with both (5) and (6), since Ellen does not have a part with the same mass as Miriam, yet the standard model is not (and should not be) taken to be inconsistent with mass’s additivity. So, while additive quantities have a very close connection to mereology, a quantity’s being additive is not sufficient to support an M-R account of its structure.

In Perry (2015), I argue that some quantities put stronger constraints on the mereology of their instances than what additivity requires. These quantities I call “properly extensive”^¹³ (recall that the unmodified term ‘extensive’ is equivalent to ‘additive’). The properly extensive quantities comprise a sub-class of the extensive quantities (quantities which are extensive but not properly so I call “merely additive”). Some quantities we classify as additive are, I claim, also properly extensive—specifically length, area, volume, temporal duration, and the invariant relativistic interval. Properly extensive quantities put stronger constraints on the relationship between quantitative structure and mereology than merely additive ones, like charge or mass, do.^¹⁴ Most importantly, properly extensive quantities, intuitively, satisfy (5) and (6).

The connection that properly extensive quantities have to the parthood structure of their instances is what makes them amenable to the M-R account’s definitions of the quantitative relations. This amounts to more than just a restriction on the range of applicability of the account. It tells us how and why the M-R definitions work when they do. That is, the M-R account, on its own, only tells us that our representations of Q are faithful insofar as the structure of the mathematical entities we appeal to mirrors the mereological structure of that quantity’s instances, and the distribution of intrinsic Q-properties over that structure. The proper extensiveness of Q tells us why there’s a necessary correspondence of this sort between the mathematical and the mereological. This is what it means to say that the success of our mathematical representations of these quantities is explained by their connection to parthood.

1.4 Aside: But what about Extended Simples?

Saying volume is properly extensive commits us to significant constraints on the possible physical structure of voluminous entities. Properly extensive quantities are unique in that these mereological constraints can require that a voluminous object have parts of a certain sort. One might wonder whether this puts a claim that length or volume is properly extensive in conflict with certain theses about mereology. In particular, the view that spatially extended mereological simples are possible.^¹⁵ Extended simples are mereologically simple, which just means that they do not have any parts except themselves. However, unlike the mereologically simple massive point particles I mentioned earlier, they are also spatially extended, which is just to say that their length, area, and/or volume is non-zero.

The most commonly discussed kind of extended simple is a mereologically simple physical body that is spatially extended, yet occupies a region composed of smaller sub-regions (“simple body/composite region”). For instance, a 2m spherical hunk of matter, with no proper parts, occupying a 2m spherical region of Euclidean 3-space. Another sort of extended simple^¹⁶ would be one which fully occupies a simple region—i.e. a region with no sub-regions (of non-zero volume). If space turns out to be composed of tiny, discrete “cells”, then a physical particle occupying the smallest possible region will not be a point-sized simple but an extended one (“simple body/simple region”).

Neither of these cases is inconsistent with length, area, or volume’s proper extensiveness, though there are a few steps required to see exactly why that is. Volume, fundamentally, is a property of regions of spacetime and, to the extent that a material object can be said to have a volume, they only have volume derivatively. Material bodies, that is, have the volumes they do in virtue of occupying a region of that volume. The constraints that properly extensive quantities put on the mereology of their instances only apply to the entities which possess volume non-derivatively. If we accept this, then an extended simple body occupying a composite region of non-zero volume is entirely consistent with volume being a properly extensive quantity. So volume’s proper extensiveness is not a threat to the possibility of the “simple body/composite region” type of extended simple.^¹⁷

On the face of it, nothing about the second kind of extended simple (“simple body/simple region”) is inconsistent with the proper extensiveness of volume. I’ve already claimed that volume’s proper extensiveness is compatible with space or spacetime being discrete. However, we can get a problem if we add the requirement that some of these extended simple bodies differ in size (i.e. one simple is more voluminous than the other). This does conflict with volume’s proper extensiveness, since the differences in size between the simples would be grounded in the different volumes of the regions they occupy. But if volume is properly extensive, then no two simple regions could differ in volume! Whenever there’s a simple extended region, R (i.e. a region of non-zero volume with no proper sub-regions), there can exist no regions that are less voluminous than R—since, if there were, then R would have to have a proper part of that volume, and so wouldn’t be simple.

So volume’s proper extensiveness rules out there being two simple regions that differ with respect to their volumes. Extended simple bodies of the “simple body/simple region” type are, therefore, only possible if they are all equivoluminous, since extended simple regions are only possible if they are all equivoluminous. Luckily, it’s generally only the first sort of simple that most fans of extended simples want to allow.^¹⁸ And, of the version of the second type of simple which are discussed at all, it’s largely the version of that simple that’s consistent with length’s proper extensiveness, primarily by those interested in the possibility of certain kinds of discrete spaces.^¹⁹

1.5 The Rest of the Paper

Sections 3 and 4 make good on the promises made in this section. There, I present a formal M-R account of volume which takes the necessary constraints obeyed by properly extensive quantities as axioms.^²⁰ From the assumption of volume’s proper extensiveness, and very little else, we can show that the volume ordering and summation relations, as defined by the M-R account, and the volume ratio relations, whose M-R definitions are generated by the “ratio procedure” (formally defined in section 4.2), are faithfully represented by the arithmetical ordering, summation, and ratio relations on the real numbers. Section 5 concludes and clarifies some issues set aside in the previous sections. Before presenting the formal M-R account of volume, it will be useful to understand how and why its competitors end up committed to quantitative structure, in particular metric structure, being radically extrinsic.

2. The Extrinsicality Worry

The M-R account defines volume metric relations in an intrinsic way. I have claimed that this is the result we should want. That is, insofar as we take quantitative structure to explain (or be part of the explanation for) physical phenomena, we should, thereby, want our account of what that structure is to render it (or the relevant sub-structure) intrinsic to the systems it’s called upon to help explain. Consider, for instance, a cruel twist on the iced coffee scenario from the introduction: On this variant, the straight path from my body to the desk is shorter than my arm, but the ratio of the path’s length to my arm’s is 0.96-to-1. Even though I am close enough to reach the iced coffee, my fingertips can only just brush the sides of the cup, and, so, it remains frustratingly out of my grasp. The M-R account locates the source of the explanatory power of the numerical ratio 0.96-to-1 in the intrinsic properties and mereological structures of the physical entities involved (or the regions they occupy). Other accounts of quantity fail to do justice to the intrinsicality intuition. Let me explain why:

I have mentioned before that most other accounts take ordering and/or summation relations (or an analogue) as primitive, posit some axioms that these relations obey, and use them to ground metric structure.^²¹ These accounts ground metric structure holistically, by appealing to representation and uniqueness theorems. These are theorems that say a given domain (like the set of all that quantity’s instances), over which some relations (the primitive ordering and summation relations) are defined that satisfy certain axioms, can be well represented by some mathematical structure or structures.

These theorems naturally suggest a certain way of defining the length ratio between x and y. Specifically, x and y’s lengths stand in a ratio of n-to-1 just in case they imply that any function from (equivalence classes of same-lengthed) lengthy objects to real numbers, which preserves the ordering and summation of the domain, maps x and y to numbers that, respectively, stand in the mathematical ratio n-to-1. That is,

(7) x is n-times the length of y ↔ For any function, f , from the set of lengthy objects to $ℝ$ , if f is such that (for any lengthy a, b, and c) b is at least as long as a ↔ f (a) ≤ f (b), and c is as long as a and b put together ↔ f (a) + f (b) = f (c), then f (x) = n * f (y). And there exists at least one such function.

A definition based on this biconditional would, clearly, be radically extrinsic. It would make “n-times the length of” dependent on the properties of certain functions from the total domain of lengthy objects to the real numbers. We might hope that the physical facts appealed to in order to prove the representation and uniqueness theorems may be used to give us an intrinsic definition. However, problems arise because representation and uniqueness theorems prove that a domain is homeomorphic to a given mathematical structure by appealing to global properties of a domain. Specifically, in addition to assumptions about and the distribution of ordering and summation relations (or some other sub-metrical analogue) over those domains, they make “structural” assumptions about the domain itself—i.e. that it is well populated, or that it has sufficient variegation in which of that quantity’s magnitudes are instantiated.

Let me give a concrete example. What sorts of definitions would be available to an account based on one of the measurement theoretic systems of Krantz et al. (1971)? Consider the definition we get from Krantz, et. al.’s definition of a function from objects to numbers used to prove a representation theorem about “Archimedean Ordered Local Semigroups”, which means a domain of entities with an ordering relation (Ordered) and summation operation on them such that no lengthy object is infinitely longer than any other (Archimedean), and the “sum” operation ‘○’ needn’t be defined for every pair of objects of the domain (Local Semigroup). It’s plausible that length is such a quantity:^²²

(8) x is n-times longer than $y = d f lim m → ∞ N (x m, y) N (x m, x) = n$

Where $n ∈ ℝ$ , and the term ‘N(x, y)’ denotes the maximum number of objects with the same length as x such that y is longer than the sum of their lengths, and x₁, x₂, x₃, … are an infinite sequence of lengthy objects whose lengths converge on 0m in the limit.

This definition makes appeal to entities whose existence is only ensured by certain “existence and richness” axioms on the domain. Specifically, Krantz, et al. use what they call a “solvability” axiom, which assumes that the domain contains an object that “solves” any “inequalities” between a given pair of its elements. So, if a is shorter than b, there’s some c such that a is as long or longer than b and c put together. This axiom will be required to ensure that each of the smaller and smaller x_i’s exist, and that they converge on 0m. Another existence axiom is required in order to ensure that enough “copies” (i.e. other objects with the same length) of each of the x_i’s exist. Without them, the term N(x, y) isn’t guaranteed to denote the right number. Moreover, while the total domain of lengthy objects is expected to satisfy these axioms, Krantz et al. warn against thinking that this means they’d be satisfied by a subset. They write that “..an axiom such as solvability may be false if attention is restricted just to that subset of objects tested: the solution to some inequality or equation may lie outside that subset. In fact, we may have accepted solvability to begin with because of the fine grainedness of the entire object set.” (Krantz et al., 1971, p. 28, my emphasis).^²³

It’s easy to see, then, how an account that employs “global” structural assumptions which apply over the domain taken as a whole, but not necessarily to a given subset, could fail to give an intrinsic account of metric structure. There is no guarantee that there is enough structure in the subsystem consisting of just x, y, and their parts to recapture metrical ratio relations.

Second-order Extrinsicality Objection

Some, like Mundy (1987), have thought that the problem with these existence and richness assumptions about the domain comes from their contingency. Representation and uniqueness theorems rely on global structural assumptions that are not guaranteed to be satisfied by a given subdomain. But, so the worry goes, its possible that a given subdomain have been all that there is. It seems to me, however, that this contingency is only a symptom of the broader problem of extrinsicality. We think the metric relations between elements of a given sub-domain (of the lengthy objects, say) would have still obtained had that subdomain been all that there is because we think that length metric relations do not depend, for their instantiation, on anything outside their relata. This is an important result, if correct, since most accounts of quantitative structure which successfully avoid the contingency objection still render metric relations radically extrinsic.

For instance, Mundy (1987) posits primitive second-order relations of “ordering” and “summation”, which relate mass^²⁴ properties. He accepts a Platonism about properties according to which these universals, and the primitive second-order quantitative structural relations they stand in, are necessary existents. The first-order comparative mass relations between objects are all grounded in higher-order relations between their properties, which allows Mundy to avoid the contingency objection.

Consider, for instance, his definition of “less massive than”:

(9) x is less massive than y =_{d f} there exist mass universals U₁ and U₂ such that U₁(x) and U₂(y) and U₁[<]U₂ (where [<] is the primitive second-order ordering relation).

No problem there. An instance of the primitive [<] relation doesn’t depend on anything, so its obtaining doesn’t depend on things extrinsic to U₁ and U₂ – or x and y for that matter. If x being less massive than y depends on their intrinsic properties standing in a primitive two-place relations, then “less massive than” is not an extrinsic relation. However, when we move from the ordering relations to metrical relations, things don’t look so good.

(10) x is n-times as massive as y =_df ∃ U₁, U₂ such that…

U₁(x) and U₂(y) and: (1) U₁ and U₂ are part of a domain of mass universals M such that the distribution of the primitive second-order ordering and summation relations over this domain satisfies axioms A₁, A₂, A₃, … ; (2) U₁ and U₂ are such that there’s a function φ, from M to $ℝ$ – where for any universals a, b, c ∈ M, a[<]b iff φ(a) < φ(b), and ab[*]c iff φ(a) + φ(b) = φ(c), and $φ (U 1) φ (U 2) = n$ ).

Where ‘[*]’ is the three-place second-order summation relation over the mass universals. Here this definition, again, just depends on universals and the fundamental ordering and summation relations they stand in. If universals are necessary existents, and if the axioms governing the primitive second-order relations over them are necessary, then this definition avoids any contingency worry we might have. However, this doesn’t help at all with the problem of extrinsicality. The obtaining of a given metric relation between a and b will (in part) depend on universals neither a, b, nor any of their parts instantiate, and on the primitive relations those universals stand in.

Field and Extrinsicality

The only account that comes close to avoiding extrinsicality is Field’s. The part of his account which fares best is the theory of spatial (or spatiotemporal) distance. Intrinsicality is a bit different for a relational quantity like distance. We shouldn’t think of facts about the distance from a to b as needing to be intrinsic to a and b. Rather, we should think of them as a matter of being intrinsic to (the shortest) straight path from a to b. If this is right, then Field’s definition of “the distance from x to y is twice that from z to w” (which we’ll express as ‘xyR₂zw’) in terms of betweenness and congruence does satisfy the intrinsicality condition:

(11) xyR₂zw ↔ ∃u(u is a point ∧ u is between x and y ∧ xuConguy ∧ uyCongzw)

This relation between x, y, z and w is intrinsic to the straight lines xy and zw. It holds in virtue of the existence of a part, u, of xy, and the fundamental congruence relation, ‘Cong’, between zw and some parts of xy. This definition of “R_n” is only available for rational n; irrational metric relations (like “the distance from x to y is π-times the distance from z to w”) are more difficult to define on this account. However, there’s at least some reason to believe that these will be either intrinsic or, at least, not radically extrinsic.^²⁵

Unfortunately, Field’s success does not extend to monadic quantities like length, mass, volume, or temporal duration.^²⁶ Field (1980) describes how to extend his account to apply to scalar quantities: replace the spatiotemporal “betweenness” and “congruence” relations with “SC-betweenness” and “SC-congruence”^²⁷ (‘SC’ for scalar). However, the analogue of Field’s definition schema using these relations does not avoid the extrinsicality problem. That is, the scalar analogue of (11),

(12) xyV₂zw ↔ ∃u(u is a voluminous body ∧ u is SC-between x and y ∧ xuCuy ∧ uyCzw).

is not an intrinsic relation. This is because, while the spatiotemporal relation “between(yxz)” entails that x is a part of physical straight line yz, its scalar analogue “SC-between(yxz)” merely indicates that y ≼ x and x ≼ z where ≼ is that quantity’s ordering relation. With no guarantee that x is part of either y or z, the relation V₂(xy) according to the scalar version of definition 11 will not be intrinsic to x, y, or their fusion. The same will go for an application of this definition schema to other scalar quantities, like mass, temperature, length, or area.^²⁸

Aside: Just how intrinsic is the the M-R account?

One might wonder if the M-R account faces a version of the extrinsicality worry, insofar as it is taken to apply to macroscopic “solid” voluminous material bodies like apples, chairs, people, and automobiles.

Here’s the concern: we ascribe approximate volumes to medium-sized dry goods like tables or swarms of bees based not on the combining the volumes of their miniscule parts (which, on an atomic theory of matter, would be extremely small), but based on the volume of some salient contiguous, simple, table-shaped region (or, rather, a class of very similar regions) throughout which those parts are distributed. But, if the table is composed of only those material parts, then this volume attribution appeals to a region that the table does not occupy.

I will take it as uncontroversial that the volume of a spatial or spatiotemporal region is intrinsic to that region.^²⁹ Whether the volume of a particular hunk of matter occupying that region is intrinsic to that hunk of matter will depend not just on what you think matter is, but also on your preferred definition of intrinsicality.^³⁰

However, I think we can safely set the differences between specific definitions of intrinsicality aside for two reasons: First, the intrinsicality intuition is the intuition that the things playing into our physical explanations be features of, or entities involved in the physical phenomena to be explained. Insofar as the volumes of macroscopic material bodies make a difference in the physical world, it is the approximate volumes we ascribe to them based on the regions they trace out (and not the sum of its microscopic voluminous parts, supposing it has any). And so the M-R account, on which the volume ratio relations between voluminous regions are genuinely intrinsic to those regions, satisfies the spirit of the intrinsicality intuition for medium-sized dry goods insofar as their macroscopically-relevant volumes depend on those regions. Again, this is because whenever the volume of a macroscopic material body is “involved in” a particular physical phenomenon, the volume of the contiguous bounding region it (partly) occupies is thereby also so involved.

Second, the intrinsicality intuition is dialectically important because it distinguishes the M-R account from its competitors: The M-R account satisfies the intuition; its competitors don’t. But, as we’ve now seen, the extant competitors to the M-R account (with the partial exception of Field) don’t merely fall short of satisfying the intrinsicality intuition, they’re views on which volume ratio relations are radically extrinsic. In most cases, volume ratio relations were grounded in holistic structural facts about the global domain of actual voluminous entities (or of all volume properties, in the second-order case). The extrinsicality of these theories isn’t anywhere close a borderline case.^³¹ So, even if what the M-R account achieves falls short of genuine intrinsicality according to the demands of a specific definition, the M-R account still does much much better, in this regard, than any available alternative. This is sufficient for my purposes.

3. A Mereological-Reductive Theory of Volume

In this section and the next, I present a formal M-R account of the quantitative structure of spatial volume,^³² and show how this account generates definitions of the volume ratio relations. The M-R definitions avoid appeal to mathematical entities or to material entities outside of the relata and their parts. I will highlight the importance of volume’s proper extensiveness in this theory, and make it clear how analogous M-R accounts for other properly extensive quantities can be constructed.

3.1 Mereology

This system assumes the axioms of classical extensional mereology (CEM).^³³

(P 1) P x x (P 2) (P x y ∧ P y z) → P x z (P 3) ¬ P y x → ∃ z (P z y ∧ z ≠ y ∧ ¬ O z x) (Sum) ∃ z (z ∈ S) → ∃ x (∀ w (w ∈ S → P w x) ∧ ∀ w (P w x → ∃ y (y ∈ S ∧ O w y))) O x y = d f ∃ z (P z x ∧ P z y) C x y z = d f P x z ∧ P y z ∧ ∀ w (P w z → (O w x ∨ O w y))

‘Pxy’ reads “x is a part of y”. According to this system, parthood is reflexive (P1) and transitive (P2). I also assume the principle of strong supplementation (P3),^³⁴ and unrestricted composition: (Sum) says that for any (non-empty) set of objects, there exists an object, x, which is their mereological sum. The predicates ‘Oxy’ and ‘Cxyz’ are to be read, respectively, as “x overlaps y” and “x and y compose z”.

3.2 Shared Properties

On the M-R account, volume is a determinable quantity associated with a class of fully determinate magnitudes, i.e. intrinsic volume properties. Since each such property is a fully determinate way of having volume, an object can instantiate at most one volume property. Let’s introduce the two-place predicate ‘≈’. x ≈ y just in case x instantiates the same determinate volume property as y. It can be pronounced more simply as: “x has the same volume as y”, or “x is as voluminous as y”. Those who are uncomfortable embracing a realist conception of properties, or who are sympathetic to comparativism^³⁵ about quantities, may accept a variant of my account on which ‘≈’ is not a derived relation, but an unanalyzed primitive two-place predicate.^³⁶ The rest of my presentation will be consistent with either approach (that is, I will not need to make any appeals to volume properties outside of my use of ‘≈’).

Since the determinate volume properties exclude one another, if x instantiates a different volume determinate from y, it follows that x doesn’t instantiate the same volume determinate as y. From this, and the symmetry and transitivity of identity, we can derive:

(≈ Sym) ∀ x ∀ y (x ≈ y → y ≈ x) (≈ Trans) ∀ x ∀ y ∀ z ((x ≈ y ∧ y ≈ z) → x ≈ z)

I will pronounce ‘x ≈ x’ as “x is voluminous” (since x ≈ x just in case x instantiates a determinate volume property). From (≈ Sym) and (≈ Trans) we can derive a limited form of reflexivity: if x bears ≈ to anything, then x is voluminous, i.e.

(≈ Ref) ∀ x (∃ y (x ≈ y) → x ≈ x)

3.3 Combination Principle

Let me introduce the three-place predicate ‘xy ○ z’, which stands for “x and y are put together in the right way and compose z”, or “x and y concatenate to make z”.^³⁷ The definition of ‘○’ differs between different quantities. For voluminous objects, all that is required for a and b to be put together in the right way is for them not to overlap:

a b ○ c = d f ¬ O a b ∧ C a b c

The defined-up ‘○’ predicate can be used to formulate axioms that apply to quantities like length or temporal duration just as well as they apply to volume. That is, while different properly extensive quantities will disagree about what’s required to be “put together in the right way”, they will agree about the overall structure of the axioms. Hence, one could straightforwardly adapt this system to apply to a quantity like length, temporal duration, or the invariant relativistic interval, simply by introducing a different definition for ‘○’.^³⁸

In general, a combination principle encodes the role of ‘○’ or ‘put together in the right way’, however it’s defined, in a broader account of that quantity’s structure. When it comes to the Volume Combination Principle, or (V-Comb), we encode the role of ‘○’ as it’s defined for volume (above) in our account of volume’s quantitative structure. That is (filling in ‘○’s definition): if a and b are voluminous, don’t overlap, and compose c, then c is voluminous.^³⁹

(V-Comb) a ≈ a ∧ b ≈ b ∧ ¬ O a b ∧ C a b c → c ≈ c

3.4 Sub-Metrical Quantitative Structure

The M-R account defines “a is less voluminous than b”, or ‘a ≺ b’, and “a is at least as voluminous as b”, or ‘a ≼ b’ as follows:

(13) a ≼ b =_df ∃x(Pxb ∧ x ≈ a)
(14) a ≺ b =_df a ≼ b ∧ a ≉ b

That is, a is less voluminous than b just in case they differ in volume and a has the same volume as one of b’s parts. The M-R account defines “c is as voluminous as a and b put together” (or “c’s volume is the sum of a and b’s volumes”) as “there exists some x ≈ a and y ≈ b such that xy ○ c”.

3.5 Totality

One reason to choose spatial volume as our example is that the ordering relation on voluminous objects is, plausibly, a total order. That is, if a and b are voluminous but don’t have the same volume, then either a’s volume is greater than b’s or vice versa.

(Totality *) a ≈ a ∧ b ≈ b → (a ≼ b ∨ b ≼ a)

Put another way: for any voluminous a and b, a is either less voluminous than, more voluminous than, or of the same volume as b. (‘a ≼ b ∨ b ≼ a’ is equivalent to ‘a ≺ b ∨ b ≺ a ∨ a ≈ b’). Not all properly extensive quantities satisfy unrestricted totality. While all of them satisfy some form of a totality axiom, for some quantities their ordering is only total within certain sub-domains.^⁴⁰ The M-R account should be, and, indeed, is, applicable to those properly extensive quantities as well.

Expressed in the fundamental, mereological terms of the M-R account, the totality axiom satisfied by volume says:

(Totality) a ≈ a ∧ b ≈ b → ∃ x ((P x b ∧ a ≈ x) ∨ (P x a ∧ b ≈ x))

In prose: If a and b are voluminous, then either a has the same volume as some part of b or vice versa.

3.6 Proper Extensiveness

The axioms (Additivity) and (Prop. Extended) jointly characterize volume’s proper extensiveness. I’ll discuss them in turn.

(Additivity) a ≈ a ∧ b ≈ b ∧ a b ∘ c → ∀ x ∀ y ∀ z (x ≈ c ∧ y z ∘ x → (y ≈ a → z ≈ b))

(Additivity), takes a bit of unpacking. All properly extensive quantities are additive: if a and b concatenate to make c, then c’s volume is the “sum” of a’s and b’s volumes. Importantly, if a and b’s volumes sum to c’s, then c’s volume cannot be the sum of a’s volume and some volume other than b’s (just as 6 + 9 = 15 means that 15 cannot be the sum of 6 and some other number ≠ 9). Here’s how this feature is encoded in the axiom (Additivity): If z is a voluminous object composed of voluminous x and y, put together in the right way, then either x ≈ a and y ≈ b , or vice versa (since a and b’s volumes sum to c’s volume), or neither x nor y share their volumes with a or b.

(Prop . Extended) a ≈ a ∧ P a b ∧ b ≈ d → (a ≈ b ∨ ∃ x ∃ y (x ≈ a ∧ y ≈ y ∧ x y ∘ d))

(Prop. Extended) has two jobs (indeed, my original temptation was to break it into two distinct axioms). If we take the M-R definitions on board, then (Prop. Extended) is equivalent to saying that (1) the ≼ ordering on voluminous objects is transitive, and (2) whenever a is less voluminous than b, b is as voluminous as a and something else put together. If a is one of b’s voluminous parts, then anything with the same volume as b, call it d must have a part with the same volume as a. If a ≈ b, then this part is d itself; otherwise d is composed of a pair of voluminous parts, one of which has the same volume as a.

3.7 Within-object Archimedean assumption

Finally, I’ll introduce an assumption that, while not strictly necessary to obtain all the results we want from this system, greatly simplifies our presentations of the definitions in the next section. It amounts to the stipulation that there can be no voluminous entity which is infinitely more voluminous than some other one. More technically, it says that, if b is some voluminous entity, then b cannot be composed of an infinite set of non-overlapping parts, all with the same volume.

(W-O Archimedean) b ≈ b ∧ P a b → ∀ S (S = {x ∣ P x b ∧ x ≈ a ∧ ∀ y ≠ x (y ∈ S → ¬ O x y)} → S is finite)

One interesting consequence of this Archimedean assumption is that there cannot be a “zero magnitude” of volume. If by “b has zero volume” we mean that ∀a∀c(ab ○ c → c ≈ a), then the Within-Object Archimedean assumption entails that any such b must not be voluminous (i.e. b ≉ b).^⁴¹ This assumption, therefore, implies that points of space, one-dimensional lines, or two-dimensional planes in space are quite literally volume-less—they do not instantiate a volume magnitude. This doesn’t mean that we deny that these entities exist; it just means we deny that such entities are voluminous (and so aren’t picked out by phrases like “so-and-so’s voluminous parts”). I could have accepted a weakened Archimedean assumption that allows for a zero magnitude of volume, but it would add unnecessary complexity while making no difference to what the system can prove.^⁴² I discuss a more substantive way we might weaken (W-O Archimedean) in section 5.1.

4. The M-R account of Volume’s Metric Structure

This section I define a general procedure which, given a voluminous pair, a and b, determines the M-R account’s definition of the volume ratio relation that they stand in—i.e. the relation we describe with “the volume ratio of a to b is 1-to-n” or “b is n-times the volume of a” (for some real number, n). Neither the procedure, nor the definitions it generates, will require quantification over anything other than a, b, and their parts, and they will need to appeal only to mereological relations and/or ‘≈’.

4.1 Definition of the “taking out” procedure

The first step will be to define a different procedure, which I call “taking x out of y” for some voluminous x and y, which tells you how many “copies” of x can “fit inside” y, and whether there’s some remainder. The ratio procedure, we shall see, is defined in terms of repeated applications of this procedure.

To “take x out of y” is to determine the maximum number of non-overlapping proper parts y can be partitioned into such that all (except, perhaps, one) of those parts bear ≈ to x. That is, whenever we take x out of y, for x ≉ y, the procedure outputs a pair of entities: A part, r, of y such that r ≼ x, which we’ll call the “remainder”. The second is an integer (we’ll call it the “count”), which is the cardinality of a particular set, S, such that (1) every member of S bears ≈ to x, (2) no member of S overlaps any other member, (3) y is the mereological sum of all the members of S ∪ {r}.

We take a out of b, where a ≈ a and b ≈ b, as follows: If b ≺ a, then there are no parts of b which bear ≈ to a. The output of this procedure is the integer 0, and the remainder is b. If a ≈ b, then the output of this procedure is the integer 1 and there is no remainder. b ≈ a so b is the fusion of 1 copy of a without remainder. The third case, a ≺ b, is the more interesting one:

a ≺ b. So there exists a part, $a 0 ′$ , of b, such that $a ≈ a 0 ′$ . By (Prop. Extended), since a ≉ b, there exists some x such that $a 0 ′ ∘ x = b$ – Call it “d₁”. By (Totality), either d₁ ≼ a or a ≼ d₁. If d₁ ≼ a, stop. d₁ is the “remainder” of this procedure, and the “count” is 1.

If it’s not the case that d₁ ≼ a, then a ≺ d₁. So there exists a part, $a 1 ′$ , of d₁ such that $a ≈ a 1 ′$ . By (Prop. Extended), since a ≉ d₁, there exists some x such that $a 1 ′ ∘ x = d 1$ – Call it “d₂”. By (Totality), either d₂ ≼ a or a ≼ d₂. If d₂ ≼ a, stop. d₂ is the “remainder” of this procedure, and the “count” is 2.

Continue this procedure for every d_n arrived at in this way. I.e.:

If d_n ≼ a, then stop. d_n is the “remainder” of this procedure, and the “count” is n.

If it’s not the case that d_n ≼ a, then a ≺ d_n. So there exists a part, $a n ′$ , of d_n such that $a ≈ a n ′$ . By (Prop. Extended), since a ≉ d_n, there exists some x such that $a n ′ ∘ x = d n$ – Call it “d_n+1”. By (Totality), either d_n+1 ≼ a or a ≼ d_n+1. If d_n+1 ≼ a, stop. d_n+1 is the “remainder” of this procedure, and the “count” is n + 1.

From this definition, it’s easy to see that taking a out of b has a defined output for any voluminous a and b.^⁴³ This procedure is unique up to the volume of the remainder, and taking x out of y, where x ≈ a and y ≈ b, has the same output (up to the volume of the remainder) as taking a out of b.

When d_n ≈ a, then a “goes evenly into” b—i.e. b can be partitioned into n + 1-many non-overlapping parts, all ≈ a. This brings us to our first Lemma, which says that whenever there is a minimal element,^⁴⁴ u, every voluminous entity is the fusion of k non-overlapping parts all ≈ u, where k is some integer.

Lemma 1. If there exists a minimal element, call it u, – that is, if ∃u∀x(x ≈ x → u ≼ x) – then, for all voluminous b, the remainder d_n left after we take u out of b bears ≈ to u.

Proof. Since d_n is part of the output of taking u out of b, it must be that this procedure terminated with d_n. Hence, by the definition of the procedure, d_n ≼ u. But, by the minimality of u, u ≼ d_n. Hence, by the definition of ≼, u ≈ d_n. □

4.2 Volume Ratio

We use the procedure for “taking x out of y” to define the volume ratio relations—i.e. those designated by statements like “b is n-times the volume of a” for some $n ∈ ℝ$ and voluminous pair a, b. We will define a “ratio procedure” which, as I mentioned before, will consist of repeated application of the taking out procedure: first taking a out of b and then, if there’s a remainder, taking that remainder out of a, and so on. Each application of the taking out procedure gets us a better and better approximation of the ratio of a to b.

After defining this procedure I show how it allows us to generate the M-R account’s definitions of volume ratio relations, and I’ll argue that the relations picked out by this procedure are ratio relations properly-so-called. The relations themselves will not require appeal to, or quantification over, numbers or other mathematical objects. The M-R definition will make use of nonnegative integers, but only in the case where they serve to count the members of some well specified, finite class of voluminous entities.

4.2.1 The Ratio Procedure

This procedure consists of repeated applications of the “taking out” procedure. We construct a list of integers K_(a,b) = 〈k₀, k₁, k₂, …, k_i, …〉, which need not be a finite list. Each successive entry, k_i, in the list K(x, y) is determined by the “count” output by each application of this procedure, as defined above. The “remainder” output by the i-th “taking out” procedure is used to indicate whether the list should continue after its i-th member, and, if it should, then that remainder also serves as one of the inputs for the next application of that procedure.

We want to find the volume ratio between a ≈ a and b ≈ b. To do this, we perform the ratio procedure on the ordered pair 〈a, b〉, which generates an ordered list, K(a, b) = 〈k₀, k₁, k₂, …, k_i, …〉 (where $k 1, k 2, …, k i, … ∈ ℤ +$ and $k 0 ∈ ℤ + ∪ {0}$ ), as follows:

0. If a ≈ b, then taking a out of b yields a count of 1 and no remainder. In that case set k₀ = 1 and stop. k₀ is K(a, b)’s first and final entry. If a ≉ b, proceed to step 1.

1. Take a out of b. This procedure will output a count, $f ∈ ℤ$ , and a remainder, call it ‘r₁’. By the definition of this procedure, r₁ ≼ a, if it exists (since, if not, the procedure would not terminate at r₁).

1-(i): If r₁ ≈ a, then set k₀ = f + 1 and stop. k₀ is K(a, b)’s first and final entry.

1-(ii): If r₁ ≉ a then r₁ ≺ a. In that case, set k₀ = f and proceed to step 2.

2. Take r₁ out of a. This procedure will output a count, $g ∈ ℤ$ , and a remainder, call it ‘r₂’. By the definition of this procedure, r₂ ≼ r₁.

2-(i): If r₂ ≈ r₁, then set k₁ = g + 1 and stop. k₁ is K(a, b)’s second and final entry.

2-(ii): If r₂ ≉ r₁ then r₂ ≺ r₁. In that case, set k₁ = g, and proceed to step 3.

In the general case, the N-th step of the construction of K(a, b) is:

N. Take r_n−1 out of r_n−2. This procedure will output a count, $h ∈ ℤ$ , and a remainder, r_n. By the definition of this procedure, r_n ≼ r_n−1.

N-(i): If r_n ≈ r_n−1, then set k_n−1 = h + 1 and stop. k_n−1 is K(a, b)’s n-th and final entry.

N-(ii): If r_n ≉ r_n−1 then r_n ≺ r_n−1. In that case, set k_n−1 = h, and proceed to step N + 1.

There is no guarantee that the ratio procedure will end for any given a and b. However, this procedure is explicitly defined and so can be used to generate a determinate ordered list, K(a, b), of integers. The list K(a, b) is, therefore, defined for any voluminous a and b. In the cases where this procedure does terminate, it also outputs a “final remainder” r_final.

4.2.2 Significance

Observe that, in cases where this procedure terminates, we have a perfect approximation. That is, a and b are both fusions of some integer number of non-overlapping parts all ≈ r_final. Let’s call these integers p and q, respectively. This means that we can characterize how much more voluminous b is than a by comparing how many different “copies” of r_final can “fit” in each. That is, the ratio of b to a is represented by $q p$ _.

Let ‘Vrat:n (x, y)’ be the two-place relation we attribute to x and y when we say “x is n-times as voluminous as y”. We now have a way to determine the ratio between b and a when the ratio procedure for a and b terminates: where p and q are the integers arrived at according to the process described in the last paragraph, then b is $q p$ -times as voluminous as y, i.e. Vrat: $q p$ (b,a).

There is another way to arrive at $q p$ using the list, K(a, b), which doesn’t appeal to r_final. Recall that K(a, b) = 〈k₀, k₁, k₂, …, k_n〉, where each k_i is a non-negative integer (and is non-zero for i ≥ 1). We can take these integers and use them to construct what is called a “simple continued fraction” of the form:

k 0 + 1 k 1 + 1 k 2 + 1 k 3 + ⋱ + 1 k n

We can write this more compactly as

k 0 + 1 k 1 + 1 k 2 + 1 k 3 + … 1 k n

For a ≼ b where the ratio procedure for a and b terminates, and K(a, b) = 〈k₀, k₁, k₂, …, k_n〉,

q p = k 0 + 1 k 1 + 1 k 2 + 1 k 3 + … 1 k n

So the list K(a, b), in cases where the ratio procedure for a and b terminates, can be used to characterize the ratio between a and b just as well as the remainder r_final. That is, it can also allow us to determine that Vrat: $q p$ (b, a). This is good, because in the cases where the ratio procedure for a and b doesn’t terminate, we do not have a final remainder, but we do have a (non-terminating) list K(a, b).

In the non-terminating case, we can still use K(a, b) to determine the ratio between a and b, despite the fact that K(a, b) is an infinite list. In the cases where K(a, b) is non-terminating, i.e. K(a, b) = 〈k₀, k₁, k₂, …〉, then we will be able to construct what is called an “infinite simple continued fraction”.

k 0 + 1 k 1 + 1 k 2 + 1 k 3 + …

Infinite simple continued fractions, it turns out, always converge on particular real numbers. In fact, one very cool feature of continued fractions is that, defined as I have done so, every positive real number can be uniquely expressed as a simple continued fraction.^⁴⁵

Each step of the ratio procedure gives us closer and closer approximations to the ratio between a and b. Since, in this case, it does not terminate, the ratio arrived at is the limit of this procedure. The number $r ∈ ℝ$ on which each successive step of these fractions converge is the analogue of our $q p$ in the terminating case. This means that, when K(a, b) = 〈k₀, k₁, k₂, …〉:

r = k 0 + 1 k 1 + 1 k 2 + 1 k 3 + …

4.3 Volume Ratio Relations

We can now determine the general definition schema for the volume ratio relations. Recall that, b “partitions into” some class of its parts iff they are all voluminous, none of the members of that class overlap, and b is their fusion. The schema is as follows:

Vrat:n(b, a) =_df ∃r₁, r₂, … ((b partitions into: k₀ parts which bear ≈ to a, and another part, r₁) ∧ (a partitions into: k₁ parts which bear ≈ to r₁, and another part, r₂) ∧ (r₁ partitions into: k₂ parts which bear ≈ to r₂) ∧ …)

The right side of this definition is precisely the sufficient condition for the ratio procedure on 〈a, b〉 to output the particular list of integers K(a, b) = 〈k₀, k₁, k₂, …〉. This definition only involves appeal to a, b and their parts, and, beyond the mereological relations, only appeals to ‘≈’, i.e. “instantiates the same determinate volume property as”. Therefore, the volume ratio relations are intrinsic. Since every positive real number can be uniquely picked out by the simple continued fractions generated from a list K(a, b), this definition allows us to associate ordered pairs of voluminous objects with a unique real number which characterizes their volume ratio. This schema is a formalized and mereologized version of the “anthyphairetic ratio” between some pair of objects, and the ratio procedure is closely related to the process of anthyphairesis.^⁴⁶

4.4 Representation Theorem

I have argued that we can, simply by counting up the right sets of their parts, match each ordered pair of voluminous objects to a unique real number. I’ve also suggested that there’s good reason to think these numbers correctly characterize the physical volume ratio between that pair. The usual punch-line to an account of metric structure involves proving representation and uniqueness theorems. The M-R account of volume’s metric structure, however, does not need to appeal to result of such a theorem to establish that there are volume ratio relations. Representation and uniqueness theorems are not necessary to give an account of the quantitative relations we appealed to in the explanations at the beginning of this paper.

It would be possible to prove representation and uniqueness theorems about this system, but not as part of its account of volume’s metrical structure. Rather, they would show that the physical volume ratio relations I characterize above imply that these relations can be faithfully represented by the right mathematical ratios. As such, we will not need to prove the usual sort of theorem, that starts with only the ordering and summation relations over the domain of voluminous objects, and gets to the ratio relations by showing that functions from the domain to the real numbers which preserve ordering and summation all agree about certain metric facts.

We, on the other hand, can appeal directly to the volume ratio relations, whose physical definitions are fixed by the ratio procedure, and consider whether mappings from objects to numbers preserve volume’s ratio structure.^⁴⁷ As such, the M-R account grounds metric structure in a thoroughly unit-free way. That is, we do not need to specify a particular function, φ, and some arbitrary voluminous object, u, to serve as the “unit” such that the image of any other voluminous object is defined in terms of the end result of the ratio procedure u and that object. Rather, we can express a simple rule which any function φ will satisfy just in case it faithfully represents/preserves volume’s metric structure:

(RULE): If taking a out of b yields the count $k ∈ ℤ$ and the remainder c, then φ(b) = k * φ(a) + φ(c)

What (RULE) does is show a correspondence between certain basic numerical relations and certain mereological ones. This is important because the definition of the ratio procedure for a given a and b is defined entirely in terms of repeated applications of the “taking out” procedure for various pairs of a’s and b’s parts. What this means is that the very ratio procedure defined in the previous section, combined with (RULE), will be able to provide a full specification of the numerical ratio between the numbers that a function must assign to a given voluminous pair, which is provably identical to the number which characterizes the volume ratio between that pair.

That is, this rule, while simple in expression, turns out to allow us to prove what I call the Direct Ratio Theorem for volume:

Direct Ratio Theorem. Every function $φ : V ↦ ℝ +$ satisfies (RULE) if and only if:

For all a, b ∈ V, Vrat:n (b, a) iff φ(b) = n * φ(a).

Moreover, for any pair of functions φ and φ′ which both satisfy (RULE), there exists some $m ∈ ℝ +$ such that, for all x ∈ V:

φ (x) = m * φ ′ (x)

Where m is such that, if there exists some u, v ∈ V where φ(v) = φ′(u), then Vrat:m (u, v).

Rather than bothering with ordering or summation structure, this theorem concerns ratio structure directly. The proof of this theorem requires no postulation of an arbitrary unit. It directly concerns the feature which all such functions must have if they are to preserve the ratio structure of the voluminous entities. I maintain (though there is not enough room to formally demonstrate it here) that the system presented in this section is rich enough to prove the Direct Ratio Theorem.^⁴⁸

5. Conclusion

We want to understand what it is about the physical world that our mathematical representations pick out, and what it is about the world in virtue of which these representations are reliable. This is useful not just to our understanding of scientific practice, but also to a deeper understanding of the physical “quantitative structure” that we often engage with only via a mathematical surrogate. I’ve argued that, for properly extensive quantities, we can give a Mereological-Reductive account of their quantitative structure. This account is necessary, and gives reductive definitions of the relations which constitute that structure according to which those relations are intrinsic.

Here I’ll clarify some points set aside during presentation of the formal M-R account for volume, then conclude with a discussion of the quantities left out by the M-R account. I outline how the view established in this paper can help us make strides towards an account of their quantitative structure.

5.1 Archimedean Assumption

One might object that this account does rely on a contingent assumption about the structure of the domain after all, since I assume that the world is Archimedean. However, there are two reasons this assumption is acceptable. The first is that the “Within-object Archimedean property” is still an intrinsic assumption. It says, roughly, that for any two voluminous a and b, there is always a finite number of non-overlapping copies of a that “fit” in b, and vice-versa. This basically amounts to the assumption that there are no pairs of voluminous objects that stand in what we might describe as an “infinite ratio”. Since the focus of this paper is on metricality, it makes sense to simplify things for ourselves and rule this out.

However, this Archimedean assumption is not one that this system genuinely needs, even though it’s a reasonable assumption to make about the actual world. That is, if we were to drop this assumption, we could still recapture many of the results of the view. The sort of “ratio” relations we would be able to define in the non-Archimedean case would correspond to something over and above what we think of as ordinary metric structure. The right representational tool would likely be some sub-structure of the surreal numbers. I think the M-R account could be extended in this way, though I won’t argue for this in detail.

The way to go about it, I think, would be to define an equivalence relation over the quantities, such that each equivalence class contains all and only quantities which bear finite ratios to one another. We could, for instance, do this by way of something like the taking out procedure: for every x ≈ x and y ≈ y, x and y are “finitely comparable” iff there exists an $n ∈ ℝ +$ such that either x ≼ y and y can be partitioned into, at most, n non-overlapping copies with the same volume as x, or y ≼ x and x can be partitioned into, at most, n non-overlapping copies with the same volume as y.

The Within-object Archimedean assumption will hold within each equivalence class carved out by this relation, and so the M-R account, unmodified, will apply to them. Ratios within equivalence classes, then, will be finite and defined in the normal way. Ratios between voluminous entities which are not finitely comparable would be infinite. We could just define “infinite ratio” to be the failure of finite comparability. Via the ordering we could define two kinds of infinite ratios (intuitively “infinitely-many-times more voluminous than” and “infinitely-many-times less voluminous than”). It’s not clear if much else would need to be done to accommodate the non-Archimedean case, but my guess is that the M-R account of volume’s quantitative structure has the resources to capture it.

5.2 Totality

Volume is a properly extensive quantity whose ordering satisfies an unrestricted totality condition. I mentioned above that there are quantities which do not satisfy totality. Consider, for instance, the case of the invariant relativistic interval, “I”, in special relativity. If we understand the interval as measuring something like the spatiotemporal “length” of a path through Minkowski space time, then the quantitative ordering relation is not total over the domain of all spatiotemporal paths. No space-like path, i.e. a path composed of events which are each at space-like separation from all of the others, is either shorter or longer than any time-like trajectory connecting two time-like separated events.^⁴⁹ On the various ways I is represented, numerically, space-like paths are assigned negative (or imaginary) numbers, while time-like ones are assigned positive (or just real) numbers.

The ordering relation does apply, however, within each sub-domain (i.e. of all the time-like trajectories, or of all the space-like paths) and, indeed, the relation is total. So, in these cases, while I is, plausibly, a properly extensive quantity that does not satisfy (Totality) in general, there are analogues of the axiom which are satisfied by certain sub-domains. Within those sub-domains, ratio relations will be definable and faithfully representable with the right mathematical structure. These ratio relations will remain silent on the relationship between a time-like trajectory and a space-like path (since the ratio procedure for such a pair will be unperformable), but, in such a case, that’s exactly what we want.^⁵⁰

5.3 Beyond Properly Extensive Quantities

From the start (see the discussion at the start of Section 1) I have made it clear that, on the whole, the alternate theories of quantity in the literature are more general than the M-R account, in that they apply to more quantities. The M-R account has many advantages, but these advantages only extend as far as the properly extensive quantities.

Moreover, there’s no prospect to tweak the M-R account to generalize it, since the view crucially depends on a mereological feature that quantities like mass or temperature do not have. One might read this as a (perhaps defeasible) disadvantage of my account. I think this would be a mistake. Generality is a good-making feature of a theory insofar as we want to give a unified account rather than a disjunctive one. But a unified account is valuable only to the extent that it does not paper over metaphysically important distinctions.

For the M-R account, the restriction to properly extensive quantities is not a handicap of the view; it’s an explanation of what it is about these quantities that grounds their physical quantitative structure, and of what about them makes it such that this structure is faithfully represented by a given bit of mathematics. Losing the restriction to properly extensive quantities means losing the explanatory strength of the M-R account. The M-R account tells us about how the metrical structure of certain quantities is grounded in the kinds of things they are. That it does not extend to other kinds of quantitative properties, whose relationship with the physical world is different, merely shows that the explanation the M-R account provides really does turn on the characteristics I identify (namely, the proper extensiveness of these quantities).

Moreover, I think the M-R account may help us make strides in the direction of an account of the structure of non–properly extensive quantities (i.e. merely additive or intensive quantities) as well. The reason for such hope is that physical quantities do not exist in isolation, they influence, interact with, and depend on other aspects of the physical world and other physical quantities. As such, there’s prima facie justification for a “hierarchical” theory of quantity, on which the metric structure of one quantity may be grounded in/defined in terms of the metric structure of another quantity (spatial length or volume, perhaps), which is already established via independent means (e.g., by the M-R account presented here).

Burgess (1984) and (1991) demonstrates that such a theory is formally viable, by developing an account of Newtonian mechanics which generates the ratio structure of mass (and others scalars) from the distance ratios between collinear points, which is defined independently. Indeed, we may take a cue from Mach (1893) and consider whether there are genuinely physical connections^⁵¹ between the quantities, like dynamical behavior, which might give us a means to ground the quantitative structure of one in the structure of the other. That is, just as Mach attempted to define mass in terms of acceleration (or tendencies to acceleration), we might take mass ratios as determined by acceleration ratios (which, in turn, are grounded in the structure of properly extensive quantities like length or temporal duration). This would allow us to give a hierarchical account of mass’s metric structure in terms of the metric structure of properly extensive quantities.^⁵²

Notes

The number of philosophers who have contributed to this paper in some form is too great to list anywhere, let alone here. I am most indebted to Tim Maudlin who, along with Hartry Field, Cian Dorr, and Shamik Dasgupta, supervised the dissertation in which early versions of this view were defended. I am indebted to audiences at NYU, Boston University, Yale, New College of the Humanities, CU Boulder, and the University of Birmingham. I have also benefited from discussions of these issues with, among many others, Claudio Calosi, Erica Shumener, Marco Dees, Eddy Chen, Niels Martens, Trevor Teitel, Maegan Fairchild, Heather Demarest. During the work on this paper, I have been the recipient of support from the Andrew W. Mellon foundation at Rutgers, the Center for the Study of Origins at CU Boulder, the Early Career Research Fellowship at the Australian National Universty, and the SQuaRed-Ex (Scientific Quantitativeness, Reduced and Explained) Project, accepted through the 2022 Marie Slodowska-Curie Action (HORIZON-MSCA-2021 Project No. 101067459) and financed by UKRI grant guarantee (Grant Ref: EP/X022625/1). ⮭
This is not entirely uncontroversial. Some have tried to defend more so-phisticated versions of the claim that mathematical objects directly explain physical facts involving quantities, most recently Knowles (2015). ⮭
Most notably Hölder (1901), Krantz et al. (1971), and Arntzenius and Dorr (2012), as well as Mundy (1987) and Eddon (2013). I will also argue that, despite initial appearances to the contrary, this is a commitment of Field (1980) and (1984) for most quantities. ⮭
Or, in the case of second-order theories of quantity like Mundy (1987), the total domain of determinate length or volume properties. ⮭
On the reading I’m interested in here, “x has the same length as y” means simply that x and y instantiate the same (i.e. numerically identical) length property. There are other readings, on which “same length as” is a fundamentally two-place relation that constitutes another part of length’s quantitative structure. I discuss this alternative in section 3.2. ⮭
E.g. Mundy, Eddon, Bigelow and Pargetter, and (arguably) Russell posit primitive second-order relations, while accounts based on Hölder or Krantz et al. posit primitive ordering relations between, and concatenation operations on, physical objects. (Mundy, 1987), (Eddon, 2013), (Bigelow et al., 1988), (Krantz et al., 1971), (Hölder, 1901), (Russell, 1903). ⮭
That is, the fact that the M-R account does not apply to all quantities is an unavoidable consequence of its being a genuinely reductive account of quantity. A theory of physical quantities which ground their structure in the role those quantities play in the physical world cannot give the same explanatory story for two quantities with wildly different physical roles. In Section 5.3, I elaborate on why I think the restricted domain of applicability of the M-R account constitutes an explanatory advantage. ⮭
In what follows, I’m assuming that some mereological relations are either metaphysically fundamental or, if derivative, are not dependent on properly extensive physical quantities. This means the M-R account is incompatible with the “Spatial Approach” of Markosian (2014) on which all mereological relationships (between physical objects) are determined by their spatial properties and relations. The M-R account is also likely incompatible with “workings parts” views, proposed by Mellor (2008) and further defended by Williams (2008), on which the parthood relation depends on a spatially-defined “containment” condition as well as the right kind of causal relationship. Many thanks to an anonymous reviewer for pressing me on this. I discuss some of the other nuances of intrinsicality and the M-R account at the end of section 2. ⮭
Two lengthy objects are “put together in the right way”, intuitively, when they are laid end-to-end. For other quantities, being put together in the right way will amount to something different. Volume, for instance, is simpler than length in this regard; two voluminous entities are “put together in the right way” just in case they don’t overlap (or have a “volume-less overlap”, where this means either their overlap instantiates 0m³, or it’s not voluminous at all). I discuss this further in section 3.3. ⮭
In section 4.2, I formally define this procedure and show how the axioms of my account of properly extensive quantities entail that it always have a well-defined output. ⮭
The ratio procedure, as defined in section 4.2, is closely related to the process of anthyphairesis, a term derived from the Greek for “reciprocal subtraction”. Cf. (Fowler, 1987). ⮭
The IUPAC (The International Union of Pure and Applied Chemistry) “Green Book”—part of a series of manuals meant to “provide a readable compilation of widely used terms and symbols” and promote “good practice of scientific language”—defines extensiveness as follows: “A quantity that is additive for independent, noninteracting subsystems is called extensive”. p.6. There has been little discussion in the philosophical literature about additiveity itself. To the extent it has been discussed by contemporary philosophers, they have followed scientific practice, cf. (Busse, 2009), (Johansson, 1996), and (McQueen, 2015). ⮭
There is some reason to suspect that something like what I call “proper extensiveness” is what Meinong (1896) calls “divisible quantities” (‘Teilbare Größen’). However, there is also evidence that this term was used by Meinong to indicate infinite divisibility rather than a correspondence between quantitative structure and mereological structure. Instances of properly extensive quantities are not necessarily infinitely divisible (as Lemma 1, in section 4.1, below, shows). Russell (1903) uses the term in a completely different way. He treats divisibility as a quantity itself, where short lines are less divisible than longer ones, which are less divisible still than two-dimensional regions, and so on. His (1903) is also the first place I have found advocating that the term ‘extensive’ not be taken to entail divisibility. ⮭
The ‘properly’ modifier is meant to suggest, as I think is true, that this feature better characterizes the intuitive notion of extension, being extended, or measure of extent than the currently accepted sense of ‘extensive’ in terms of additivity. I won’t offer a defense of this claim here. ⮭
See Markosian (1998), McDaniel (2007), Simons (2004) for defense of, and McDaniel (2003), Spencer (2010) for discussion of arguments against, the possibility of extended simples. ⮭
Cf. Braddon-Mitchell and Miller (2006). ⮭
Things become more complicated, however, if you combine this conception of an extended simple with a super substantivalist ontology, on which physical objects are literally identical to the regions of space/spacetime they “occupy”. A region containing some matter, on this view, is just a region with the intrinsic, fundamental, and monadic “filled with matter” property. This isn’t the only way to be a supersubstantivalist. There are other, more restrictive, versions which only allow parts of spacetime to instantiate geometric properties. Cf. Skow (2005), Sklar (1974), and Sider (2001) for discussion. Regardless, most supersubstantivalists take it as given that the mereology of objects and the mereology of the regions they occupy must be the same. If the mereology of bodies must match the mereology of the regions they occupy, then volume’s proper extensiveness would rule out supersubstantival extended simples occupying differently-sized, spatially extended regions (supposing that we interpret ‘simple’ in the ordinary way). ⮭
Cf. McDaniel (2009), as well as the papers mentioned in note 15 (with the exception of Spencer (2010)). ⮭
A borderline exception to this comes from Tognazzini (2006). Tognazzini claims that, other things being equal, our definition of ‘mereological simple’ should leave open that, if it’s possible that there be material entities which occupy different-volumed simple regions, such entities would still be mereologically simple. However, Tognazzini’s carefulness shouldn’t be taken to clash with volume’s proper extensiveness. It’s philosophical best practices to, other things being equal, propose definitions of key notions that are maximally agnostic as to other philosophical views. This is a worthwhile strategy for any philosophical investigation, but such agnosticism is not meant to preclude us eventually accepting a positive theory which is more restrictive about what’s possible. ⮭
The conditions I give for properly extensive quantities in Perry (2015) make use of primitive ordering and summation relations between Q-properties. The M-R account has no such relations at the fundamental level. As such, if we want to take volume’s proper extensiveness as fundamental, we need to express the constraints it puts on the parts of voluminous objects a different way. (Note that (5) and (6) will be of no help here. Once we plug in the M-R definitions for ‘LESS-Q’ and ‘Q-SUM’, they become instances of the trivial ‘□(P ↔ P)’). In section 3.6, I show that we can articulate these constraints in terms of the fundamental posits of the M-R account—viz. mereological relations and the sharing of intrinsic determinate length/volume properties. ⮭
This is a sensible approach, since there’s little prospect in taking metric structure as primitive in any economical way. “n-times the volume of” and “m-times the volume of”, if construed as two-place relations between voluminous entities (i.e. not as relations between a pair of voluminous entities and a number), are substantively different relations, and we would have to posit distinct axioms for each and every such ratio relation if we were to take them as primitive. ⮭
Krantz et al. say that length is an “extensive structure”, which are a specific kind of Archimedean ordered local semigroup. An extensive structure is such that the ordering relation is transitive and total, and the summation operation is associative, commutative, and (regarding the length ordering) monotonic. We will not need to consider these axioms in detail, since they are not the source of the account’s troublesome extrinsicality. ⮭
I think that there’s a kernel of a good definition here. That is, I expect Krantz et al.’s definition could be modified to give one equivalent to the version I defend in section 4. Imagine a variant of Krantz et al.’s account that adds the assumption that length is properly extensive, call it “K + PE” (for “Krantz plus proper extensiveness”). One (though certainly not the only) way to achieve this would be by adding the mereological axioms I present in section 3.6. The definition of length ratio relations on K + PE is the same, except that the limit involved in (8) is replaced with:

$lim m → ∞ N * (a m, y) N * (b m, x) .$

Where a₁, a₂, a₃, … are a sequence of parts of y whose lengths approach 0m in the limit, and likewise for b₁, b₂, b₃, … and x, and every a_n is as long as b_m if n = m. And the term ‘N^*(x, y)’ is the equivalent of ‘N(x, y)’ when you restrict your quantifiers to only y and y’s parts. The K + PE does not need to rely on independent existence and richness assumptions about the domain. The existence of enough copies of each member of each sequence (the various a_i’s and b_i’s) are guaranteed by length’s proper extensiveness. Since the constraints of proper extensiveness can be understood entirely in terms of x and y’s parts, length ratio relations are intrinsic according to K + PE. However, while K + PE improves on the original in some respects, it also comes with some added disadvantages. Specifically, many of K + PE’s axioms and primitive posits are redundant. That is, proper extensiveness plus the totality of the length ordering entails all the necessary axioms of the M-R account of length (just as it would for the M-R account of volume). I argue that the M-R account for quantities like length can adequately define these metric relations (I show it for volume, below). If this is right, then we can give an adequate account of quantitative structure using only a few of K + PE’s axioms and only one of its two primitive relations (viz. length ordering). If we are interested in using proper extensiveness to give an intrinsic account in the spirit of Krantz et al.’s definition in the text, we would be much better off accepting the M-R account than we would K + PE. The M-R account is entailed by a proper subset of K + PE’s axioms, and employs no primitive quantitative relations. ⮭
A key feature of Mundy’s second-order account is its generality, the account applies in the exact same way to any quantities which share the same structure (the so-called “unsigned scalar quantities”, like length, volume, temperature (in Kelvin), etc.). ⮭
There’s a way to get closer to a general account of ratios, though it falls short of a definition. Field (1980) describes the comparison of products, | x * y| < |z * w|, which amounts to the comparison of ratios $x z < w y$ (where x, y, w, and z are either spatiotemporal distances or intervals of difference according to some scalar quantity). ⮭
The proponent of Field’s account would likely claim that the spatiotemporal scalars (length, volume, temporal duration) can be grounded in the right kind of distance facts. However, this does not yet guarantee that this grounding story will equip us with an intrinsic definition of these quantity’s metric relations. Moreover, Maudlin (1993) has argued that, even in spaces where there are points, there’s good reason to not take distance to be a fundamental quantity (though some doubt about these arguments have been expressed by Dees (2015)). Even putting those issues aside, if it turns out that space is gunky, and lacks points, it would be very implausible that distance is the fundamental spatiotemporal quantity. ⮭
If congruence is analyzed as the sharing of intrinsic properties, then positing a distinct “SC-congruence” will be unnecessary. Cf. section 3.2 ⮭
However, see note 26 ⮭
It’s certainly intrinsic according to the definition employed in Lewis (1983b): “Px is an intrinsic property just in case it supervenes on the fundamental properties x and its parts instantiate, as well as the fundamental relations that hold among x’s parts.”, as well as the stricter variant employed by Skow (2007) “Px is an intrinsic property just in case every quantifier in its analysis (in fundamental terms) is restricted to x and x’s parts.”. It’s seems similarly plausible that the volume of a region counts as ‘intrinsic’ on the “property compatible with being the only thing in the world” (cf. Kim (1982)), as well as the “non-disjunctive property necessarily shared by any duplicate” (cf. Lewis (1983a) and Langton and Lewis (1998)) definitions of the term, but I won’t argue for that here. ⮭
Regarding the nature of matter, see my discussion of extended simples and supersubstantivalism in section 1.4. Regarding accounts of intrinsicality, see note 29. ⮭
And the radical extrinsicality of this story is the same regardless of whether the global domain of voluminous entities consists of only spatiotemporal regions, or only voluminous bits of matter, or both. ⮭
I discuss some of the complications involved with spatio-temporal (as opposed to purely spatial or purely temporal) quantities in section 5.2. ⮭
I’m reasonably confident that it’s possible to get everything we want from my system using, instead of CEM, a weaker mereology that Varzi (2014) calls “minimal mereology” (MM). MM replaces (P3) with weak supplementation—’∀x∀y(PPxy → ∃z(PPzy ∧ ¬Ozx))’. Where ‘PPxy’ stands for “x is a proper part of y”, i.e. ‘Pxy ∧ x ≠ y’. The reason for this is that the other axioms in this system will ensure that voluminous objects are guaranteed to satisfy something equivalent to a restriction of (P3) (even if other objects don’t). It would also not be difficult to get most of the results we need, including all of the definitions of volume ratio relations, using a restricted composition rule (limiting fusions to, say, contiguous spatial regions). Thanks to Achille Varzi for extremely helpful discussion and advice regarding this issue. ⮭
The antisymmetry of parthood—i.e. ∀x∀y((Pxy ∧ Pyx) → x = y)—follows these axioms. ⮭
Comparativism, in the case of volume, is the view that the determinate magnitudes associated with the quantity are comparative volume relations rather than monadic volume properties. Russell (1903) distinguishes between the “relative” view (comparativism) and the “absolute” view (the view that a quantity’s determinate magnitudes are monadic properties). Comparativism about quantity (in particular, mass) has been recently defended by Dasgupta (2013). ⮭
The comparativist variant retains many of the advantages of my preferred view, with two notable exceptions: (1) the variant theory cannot derive (≈ Sym) and (≈ Trans), so has to take them as additional brute axioms; (2) Volume’s ordering, summation, and ratio relations—which are all defined, partially, in terms of ‘≈’—will not be internal relations. Internal relations, recall, are those which depend solely on the intrinsic properties of their relata. The quantitative volume relations on this variant will be intrinsic to the system composed by their relata (since they depend on the distribution of the primitive two-place ‘≈’ relation over that system), but they will not be internal, since ‘≈’, on this variant, is no longer defined in terms of sharing intrinsic properties. However, given her aversion to intrinsic volume properties in general, the comparativist is unlikely to see (2) as a great loss. I should note, problem (1) here is a much more limited version of the “conspiracy of comparative relations” problem recently discussed by Martens (2022). Likewise, Armstrong (1988) raises (1) as an objection to the comparativist position defended by Bigelow et al. (1988). ⮭
I will sometimes write this as ‘○abc’, ‘○(a, b, c)’, or ‘a ○ b = c’. The ‘=‘ in the latter formulation should not be interpreted as the identity relation. ⮭
As well as adopting the appropriately restricted variant of the totality assumption discussed in section 3.5, below. ⮭
In the general case, the combination principle is this:

$(Comb) a ≈ a ∧ b ≈ b ∧ (a, b) ∘ (c) → c ≈ c$

⮭
One such case is the invariant relativistic interval. I discuss how the totality axiom would be restricted for quantities of this sort in section 5.2. ⮭
Why? Make the weakest version of the claim that b ≈ b has zero volume,i.e. that, for some a and c, ab ○ c and a ≈ c. From this supposition, it’s easy to construct an infinite set of non-overlapping parts of c all with the same volume as b: By (Prop. Extended), since b ≺ c, and c ≈ a, it follows that there exist some b′ ≈ b and x ≈ x such that xb′ ∘ a. By (Additivity), since c ≈ a and xb′ ∘ a, it follows that x ≈ a. But this is the very position we started out in! That is, from the assumption that c can be divided into two, non-overlapping, voluminous parts, a and b, where a ≈ c, it follows that a can be divided into two non-overlapping, voluminous parts, x and b′, where b ≈ b′ and x ≈ a. This means we can repeat this process indefinitely, applying (Prop. Extended) and then (Additivity) in the same way to get infinitely many parts all as voluminous as b. ⮭
This would amount to adding an exception just for the zero magnitude: e.g. we replace (W-O Archimedean) with a disjunction stating (roughly) that, for every voluminous a and b such that Pab, either the set S (as defined in the original axiom) is finite or a is such that, for all voluminous x, if xa ○ y then x ≈ y. If we were to add this exception, no change would be required to the expression of any of the axioms. However, the definitions of the two procedures in the next section will require the addition of a “& so-and-so is not a zero-volume” qualifier at certain key steps. Cf. (Balashov, 1999) for some considerations for and against positing a zero magnitude. ⮭
Proof: Suppose a ≈ a and b ≈ b. By (Totality), either a ≺ b, a ≈ b, or b ≺ a. In the latter two cases, the result is trivial. In the case where a ≺ b, if the procedure terminates at the n’th step, then (by the definition of the procedure) b can be partitioned into n + 1 many non-overlapping parts, n of which bear ≈ to a, and one we’ll call “dn”. In that case n is the count and dn the remainder output by this procedure. So, for a ≺ b, taking a out of b can fail to have an output only if there’s no step at which the procedure terminates. However, if the procedure never terminates, then there exists a set, S, of non-overlapping parts of b such that ∀x(x ∈ S → x ≈ a) which is infinite. However, this is ruled out by the Within-object Archimedean axiom. So the procedure will eventually terminate. ⮭
Fun fact: We don’t actually need to make a global claim to establish that there exists a minimal element. Because volume is properly extensive, it will suffice to show that there exists some voluminous entity which lacks any parts with different volume. I.e.: ∃u(u ≈ u ∧ ¬∃x(P(x, u) ∧ x ≈ x ∧ x ≉ u)) alternatively ∃u(u ≈ u ∧ ∀x(P(x, u) → (x ≈ x → x ≈ u))). ⮭
See, e.g., Chrystal (1886) for proofs that any real can be expressed as a continued fraction, and that simple continued fraction expressions of positive real numbers are unique. ⮭
Also called “antenaresis” or the Euclidean algorithm. The term ‘anthyphairesis’ as the name of the process of reciprocal subtraction is from the Greek ‘anthuphairein’ Cf. (Fowler, 1987, chap. 2). ⮭
There is also a practical reason to move away from a representation theorem couched in terms of ordering and summation, which stems from the way I define volume ratios (viz. via a procedure which links voluminous pairs up to real numbers via continued fractions). The problem is this: Continued fractions are not amenable to even very simple arithmetic operations. As such, if we wanted to use the account of metricality to define a function from objects to numbers and then show that this function preserved ordering and summation structure, the proof would require an inordinate amount of complexity. Specifically, the problem is with summation structure. Continued fractions do not like being added to one another. Seriously, they hate it. Nobody even knew whether you could do it directly until someone came up with an algorithm for doing it simple enough to be performed (by a computer anyway) in 1972, and it is still extremely complicated. (That someone is R.W. Gosper in: Gosper (1972). “Continued fraction arithmetic.” HAKMEM Item 101B, MIT Artificial Intelligence Memo.) ⮭
In many ways, the previous section could be construed as a sketch of the relevant steps of that proof. Specifically, demonstrating that the taking-out procedure can be performed for any pair of voluminous entities, and that the results of this procedure—an integer “count” and a voluminous object “remainder”—represent the number of times one volume can be “subtracted” from the other until the remainder too small to subtract from anymore. If we assign numbers to voluminous entities in accordance to (Rule), then whatever number we assign to a, φ(a), must be such that the number assigned to b, φ(b), is equal to the sum of k multiplied by φ(a) and φ(c) where k is the count and c the remainder. The ratio procedure, as we’ve defined it, corresponds to the process of repeated “reciprocal sub-traction” used to determine anthyphairetic ratios. As I sketch in Section 4.2.2, above, the sequence of counts will uniquely pick out a simple continued fraction. Since the simple continued fraction expressions of positive real numbers is unique, see Chrystal (1886), then this means the ratio procedure performed on a given pair, a and b, will uniquely pick out a specific ratio (viz. the ratio between that number and 1). If we assign numbers to voluminous bodies in accordance with (RULE), then the “subtraction” here lines up with arithmetical subtraction, and applying the taking-out procedure reciprocally, subtracting the previous remainder from the previous body being “subtracted”, and so on, will mean that that same simple continued fraction generated by this procedure will determine the arithmetical ratio between φ(a) and φ(b), see Fowler (1987). Therefore, so the argument goes, any function from objects to numbers that satisfies (RULE) will map any voluminous pair to numbers whose arithmetical ratio is the same as that pair’s volume ratio. I think this can be shown more rigorously than even what I’ve presented in this paper so far. However, to prove this with full generality, we would also need to show that the taking-out procedure really is unique up to the volume of the remainder, and that there will always exist mappings from voluminous objects to numbers that satisfy (RULE), no matter how volume properties are distributed, and so on. Such a proof would require quite some space, and hanc marginis exiguitas non caperet. ⮭
Indeed, even a classical version of spatiotemporal length would obey similar restrictions. In the classical space-time, paths which cross simultaneity slices (without doubling back) would have a spatiotemporal length measurable in units like seconds or years, while paths wholly contained within a slice have spatiotemporal length measured in meters, or feet. Within each of these domains the ordering is total, but there are no ordering relations between members of either domain—a 5 meter path is neither longer nor shorter than a 12 second one. ⮭
The set of light-like trajectories pose an independent difficulty, since, on most numerical representations of I, every such path is assigned I= 0, despite the fact that, in a very real sense, proper sub-intervals of these paths are genuinely “shorter” than the paths of which they are a part (even though there are no length ordering facts about any light-like trajectories that don’t completely overlap). I think there are things to be said here, and an account of quantitative structure in terms of mereology will contribute greatly to our understanding of these issues, but a discussion of that here would take us too far afield. ⮭
Unlike, e.g., Burgess’s cross-quantity “stands in the same ratio as” relation, Q_s, which does not purport to have any physical significance beyond it being necessary for Burgess’s synthetic equivalent (in the relevant sense) to a physical theory formulated using mathematical structures like the real numbers. ⮭
Recently, Field has expressed confidence that a view of this sort may allow his theory to extend to point-masses, which his original system could not accommodate. Cf. the preface of Field (2016), as well as my discussion of Field’s position at the end of Section 2, above. ⮭

References

D. M. Armstrong. Are quantities relations? a reply to bigelow and pargetter. Philosophical Studies, 54(3):305–316, 1988.

Frank Arntzenius and Cian Dorr. Space, Time, and Stuff, chapter Calculus as Geometry. Oxford University Press, 2012.

Yuri Balashov. Zero-value physical quantities. Synthese, 119(3):253–286, 1999.

J. Bigelow, R. Pargetter, and D. M. Armstrong. Quantities. Philosophical Studies, 54(3):287–316, 1988. ISSN 0031–8116.

David Braddon-Mitchell and Kristie Miller. The physics of extended simples. Analysis, 66(3):222–226, 2006.

John P. Burgess. Synthetic mechanics. Journal of Philosophical Logic, 13 (4):379–395, 1984.

John P. Burgess. Synthetic mechanics revisited. Journal of Philosophical Logic, 20(2):121–130, 1991.

Ralf Busse. Humean supervenience, vectorial fields, and the spinning sphere. Dialectica, 63(4):449–489, 2009.

G. Chrystal. Algebra: An Elementary Text Book for the Higher Classes of Secondary Schools and for Colleges. Part II. A. and C. Black., London, (revised edition, 1900) edition, 1886.

Shamik Dasgupta. Absolutism vs comparativism about quantity. Oxford Studies in Metaphysics, 8, 2013.

Marco Dees. Maudlin on the Triangle Inequality. Thought: A Journal of Philosophy, 4(2):124–130, 2015.

Maya Eddon. Fundamental properties of fundamental properties. In Karen Bennett and Dean Zimmerman, editors, Oxford Studies in Metaphysics, Volume 8, volume 8, pages 78–104. Oxford University Press, 2013.

Hartry Field. Science Without Numbers. Princeton University Press, 1980. Hartry Field. Can we dispense with space-time? PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association, 1984:33–90, 1984.

Hartry Field. Science Without Numbers. Oxford University Press, 2nd ed. edition, 2016.

D. H. Fowler. The Mathematics of Plato’s Academy: A New Reconstruction. Clarendon Press, Oxford, 1987.

R. W. Gosper. Continued fraction arithmetic. Artificial Intelligence Memo HAKMEM Item 101B, MIT, 1972.

Otto Hölder. Die axiome der quantität und die lehre vom mass (part 1). Journal of Mathematical Psychology, 40(23):235–252, 1901. trans. Joel Michell and Catherine Ernst (1996).

I. Johansson. Physical addition. Nijhoff International Philosophy Series, 53:277–288, 1996. URL http://hem.passagen.se/ijohansson/ontology3.pdf.http://hem.passagen.se/ijohansson/ontology3.pdf

Jaegwon Kim. Psychophysical supervenience. Philosophical Studies, 41 (January):51–70, 1982. doi: 10.1007/BF00353523.10.1007/BF00353523

Robert Knowles. Heavy Duty Platonism. Erkenntnis, pages 1–16, 2015. ISSN 0165–0106. doi: 10.1007/s10670-015-9723-4. URL http://dx.doi.org/10.1007/s10670-015-9723-4.10.1007/s10670-015-9723-4 http://dx.doi.org/10.1007/s10670-015-9723-4

David Krantz, Duncan Luce, Patrick Suppes, and Amos Tversky. Foundations of Measurement, Vol. I: Additive and Polynomial Representations. New York Academic Press, 1971.

Rae Langton and David Lewis. Defining ‘intrinsic’. Philosophy and Phenomenological Research, 58(2):333–345, 1998.

David Lewis. Extrinsic properties. Philosophical Studies, 44(2):197–200, 1983a.

David Lewis. New work for a theory of universals. Australasian Journal of Philosophy, 61(December):343–377, 1983b.

Ernst Mach. The Science of Mechanics: A Critical and Historical Exposition of Its Principles. The works of Ernst Mach. McCormack, T.J. (trans.), Open court Publishing Company, 1893. URL https://books.google.com/books?id=4OE2AAAAMAAJ.https://books.google.com/books?id=4OE2AAAAMAAJ

Ned Markosian. Simples. Australasian Journal of Philosophy, 76(2):213–228, 1998.

Ned Markosian. A spatial approach to mereology. In Shieva Kein-schmidt, editor, Mereology and Location. Oxford University Press, 2014. Niels C. M. Martens. Machian comparativism about mass. British Journal for the Philosophy of Science, 73(2):325–349, 2022. doi: 10.1093/bjps/axz013.10.1093/bjps/axz013

Tim Maudlin. Buckets of water and waves of space: Why spacetime is probably a substance. Philosophy of Science, 60(2):183–203, 1993.

Kris McDaniel. Against maxcon simples. Australasian Journal of Philosophy, 81(2):265–275, 2003.

Kris McDaniel. Extended simples. Philosophical Studies, 133(1):131–141, 2007.

Kris McDaniel. Extended simples and qualitative heterogeneity. Philosophical Quarterly, 59(235):325–331, 2009.

Kelvin J. McQueen. Mass Additivity and a Priori Entailment. Synthese, 192(5):1373–1392, 2015. doi: 10.1007/s11229-014-0627-7.10.1007/s11229-014-0627-7

A. Meinong. Über die Bedeutung des Weberschen Gesetzes: Beiträge zur Psychologie des Vergleichens und Messens. Leopold Voss, 1896.

D. H. Mellor. Micro-composition. Royal Institute of Philosophy Supplement, 62:65–80, 2008. doi: 10.1017/S1358246108000581.10.1017/S1358246108000581

Brent Mundy. The metaphysics of quantity. Philosophical Studies, 51(1): 29–54, 1987.

Zee R. Perry. Properly Extensive Quantities. Philosophy of Science, 82: 833–844, December 2015.

Bertrand Russell. Principles of Mathematics. Routledge, 1903.

Theodore Sider. Four Dimensionalism: An Ontology of Persistence and Time. Oxford University Press, 2001.

Peter Simons. Extended simples. The Monist, 87(3):371–85, 2004.

Lawrence Sklar. Space, Time and Spacetime. University of California Press, 1974.

Bradford Skow. Once Upon a Spacetime. PhD thesis, New York University, 2005.

Bradford Skow. Are shapes intrinsic? Philosophical Studies, 133(1):111–130, 2007. doi: 10.1007/s11098-006-9009-4.10.1007/s11098-006-9009-4

Joshua Spencer. A tale of two simples. Philosophical Studies, 148(2): 167–181, 2010.

Neal A. Tognazzini. Simples and the possibility of discrete space. Australasian Journal of Philosophy, 84(1):117–128, 2006.

Achille C. Varzi. Formal Theories of Parthood. In Claudio Calosi and Pierluigi Graziani, editors, Mereology and the Sciences: Parts and Wholes in the Contemporary Scientific Context, pages 359–370. Springer-Verlag, 2014.

Robert Williams. Working parts: Reply to mellor. Royal Institute of Philosophy Supplement, 62:81–106, 2008. doi: 10.1017/S1358246108000593.10.1017/S1358246108000593