Medium Independence and the Failure of the Mechanistic Account of Computation

1. Elements of an Account of Computation

Different authors have presented different desiderata for an account of computation; most disagreement is not about what is desired, but which account of computation gets us what we want. In order to motivate further discussion, I will mention just a few reasonable and (mostly) uncontroversial criteria, which will then serve as points of departure for further discussion.

Let us start by accepting that not everything is computational, and that there is some fact of the matter about whether something is computational or not.³ Not everyone agrees with these assumptions, of course: Putnam (1988) argues for the view that everything is a computer (i.e., pancomputationalism), and Dennett (2008) argues that everything can be viewed as a computer if one so chooses (i.e., computational perspectivalism). These views will not be considered here; they are nonstarters if (like me) you take computational explanation seriously.

Briefly, computational explanation is the practice of explaining a phenomenon by appealing to the computations some system (literally) performs (Piccinini 2007). Nearly everything can be simulated computationally: for virtually all sciences S, one can find a journal, department, or lab doing work in “computational S”, which very often means developing and running computational simulations of the phenomena studied in S.⁴ In contrast, a small number of things can be explained via their ability to literally perform computations. Computer simulations of weather systems, galaxies, and rock strata erosion patterns are matters of course in contemporary science, but scientists do not describe these systems as doing what they do in terms of the computations those systems literally perform. On the other hand, scientists do explain neural systems and psychological systems in terms of the computations those systems perform. Without rejecting pancomputationalism and computational perspectivalism, these distinctions do not get off the ground. So, let’s assume that some things compute, some do not, and how to determine which is which is something we require of an account of computation.

One might wonder: is it really not clear what makes something computational or not? The computer industry surely knows what a computational system is, plus there is an entire discipline known as “theoretical computer science.” True on both counts! But this is not enough. Let us start with the second point. The theory of computation is wholly mathematical, and as such has nothing to say about physical objects at all, let alone which ones compute. What the theory of computation does tell us is that, once we have decided—via independent means— that something is a physical implementation of a certain automaton (e.g., a restricted Turing Machine,⁵ a finite-state machine, or a pushdown automata), there are certain limitations to what that system can do qua physically-implemented automaton. In other words, if you give me what has already been determined to be a physically-realized automaton (including a specification of which physical states correspond to computational states), then I may be able to use the theory of computation to tell you some things about that physical system qua computational system. But I cannot use the theory of computation to tell you whether a given physical system is a computer in the first place. That is simply not the purview of the theory of computation.

An analogy may help. One might wonder how many clouds are in a particular part of the sky, or if there is a prime number of individual stones in some part of a metamorphic rock layer. Why can’t we simply appeal to the part of mathematics that deals with numbers (i.e., number theory) to provide answers to these questions? Simply put, questions about how to count certain physical things (if they can be counted at all) are not the purview of number theory, because they are not mathematical questions. Once we have decided—by independent means—what to count and how to count them, then we can deploy the resources of number theory. On their own, however, mathematical theories—including the theory of computation—have nothing to say (and cannot have anything to say) about things in the physical world.

The second problem is this: what we know about artifactual computational systems is not much help in determining which natural systems (if any) are computational. In principle, computational systems can be made of all kinds of physical media; there is no in-principle barrier to a neural computational system. However, the computational systems we create are computational precisely because we have designed and created them as such. Again, if we are to take computational explanation seriously, then we need a principled way to determine which natural systems legitimately, literally compute. As before, we cannot look to the mathematical theory of computation; yet we also cannot look to the engineering and design practices that go into constructing computers. It is also not the purview of these practices to tell us what does and does not compute.

Hence, we find ourselves in need of a philosophical account of computation. Which systems are computational cannot be read off the mathematical theory of computation. And if there are natural computational systems—systems that we have not explicitly created and designed to be computers—computer engineering is no help in determining which these are. A satisfactory account of computation should provide criteria that can be used to make judgments about which natural systems are computational, while also explaining what makes artificial systems computational.

Now that the stage has been set, let us evaluate what I take to be one of the most well-developed accounts of computation on the market today: Piccinini’s mechanistic account of computation. Although this account tackles the problems mentioned above head-on, it fails to solve those problems. To be clear, many good things can be said about this account, and there is much I agree with. However, disagreement is where much of the research happens in philosophy, so let’s get to it.

2. Unpacking the Mechanistic Account

The crux of the mechanistic account of computation (again, MAC) is that computation essentially involves the processing of vehicles in a medium-independent way, dispensing entirely with the need for representations. Although computations may involve representations, we can understand computation qua computation without referring to representations whatsoever. Thus, according to the MAC, the representations or representational capacities of a system are irrelevant to whether or not it is computational.

To evaluate the MAC, we must examine the individual elements of the account, which is what I will do in this section. Along the way, I will point out its problematic aspects. Before this, a bit of context is in order. The “mechanistic” aspect of the MAC comes from the neo-mechanistic framework developed in works such as Bechtel and Abrahamsen (2005), Glennan (2002), Machamer, Darden, and Craver (2000), and subsequently widely adopted in contemporary philosophy of science. The development and refinement of the mechanistic view of scientific explanation is easily one of the most important things to happen in the philosophy of science in the last few decades. The briefest of overviews is enough for what follows.

Consider all of the the various phenomena that are candidates for scientific study. According to the mechanistic view, one subset of these things are explained by appealing to their underlying mechanisms, where a mechanism is a set of entities organized in a particular way such that their activities give rise to a phenomenon.⁶ For many sciences, especially the biological sciences, the discovery and articulation of mechanisms plays an essential role in scientific explanation.

One subset of the mechanisms consists of those that have functions. This is particularly important for understanding the MAC. All mechanisms have functions in the thin sense of having a causal-role function (Cummins 1975). After all, mechanisms do things in particular ways. But not all mechanisms have a teleological function: a purposeful function (roughly speaking). For example, one might be interested in the mechanism responsible for eye color in humans. Explaining why certain irises are green might involve appealing to the pigment found in the stroma of the iris, or the particular alleles responsible for iris coloration. This would involve a story about the causal-role functions of the various entities and activities that give rise to the green color of the iris. However, given that there is no purpose to having green eyes (or any other eye color), the green color of the iris has no teleological function. The mechanisms involved in eye color have functions only in the sense that they simply play various causal roles. In contrast, the mechanisms involved in the beating of the human heart have functions in the sense that the heart’s beating has a purpose: to pump blood.⁷

One subset of the mechanisms with functions consists of those that perform computations (according to the MAC). The general idea is that certain teleological functional mechanisms operate on “vehicles” in a “medium-independent” way (the scare-quoted terms will be defined shortly). This particular kind of processing on these particular kinds of vehicles is all that’s required for something to compute: no further requirement about the presence of information, representations, or algorithms is needed.

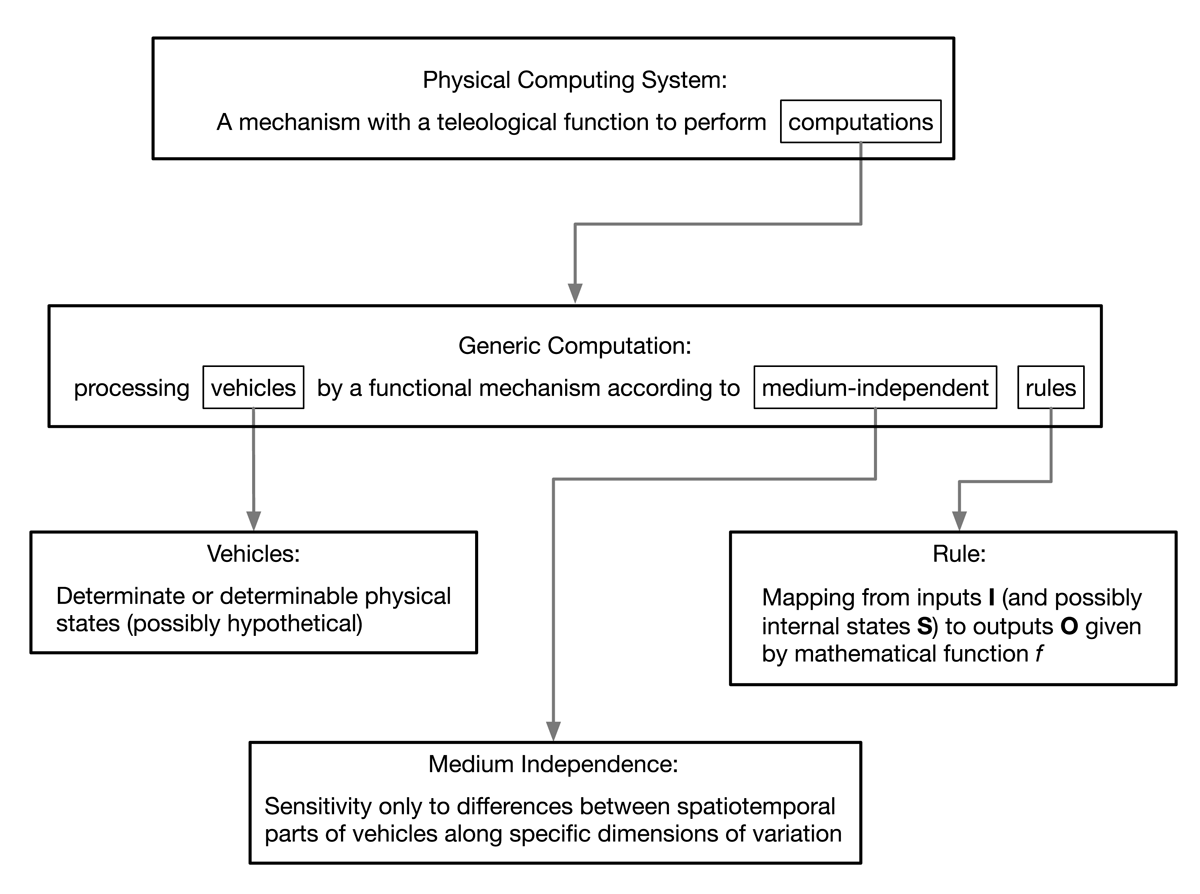
We can now turn to the precise formulation of the account. The centerpiece of the MAC is an account of physical computing systems; the official specification (slightly condensed) is given in Figure 1, adapted from Piccinini (2015: 120–21). Elements that will be further analyzed are boxed, with arrows to Piccinini’s initial characterization of each.

Two quick examples will help illustrate the way that the MAC is supposed to work. First, consider a basic calculator. Why does this count as a physical computing system? Well, a calculator is a mechanism, and it has teleological functions. One of those teleological functions is to perform calculations. Are calculations instances of generic computation? Yes, because there are mappings from inputs to outputs via internal states that follow a rule, sensitive only to differences between voltage levels in circuit elements. So how does it perform these computations? In a typical electronic calculator, this is done⁸ by appealing to the Boolean operations performed on circuits with binary values. At this level, the functional mechanism is only sensitive to differences between two voltage levels of the circuits, and follows rules that map inputs (and internal states) to outputs.

Figure 1

Figure 1

Elements of MAC.

A second example is neural firing. When a neuron’s voltage rises above a certain threshold (due to, for example, input from other neurons, or experimental intervention), it will generate a spike, or action potential. Neural spikes are the basis of much communication between neurons: when a spike reaches the end of a neuron, it causes neurotransmitters to be released, which in turn serve to generate electrical inputs to subsequent “downstream” neurons. Why does this count as a physical computing system? Well, a neuron is a mechanism, and it has teleological functions. One of those teleological functions is (we assume) to transmit spikes. Is spike transmission an instance of generic computation? Yes, according to the MAC, because spike transmission is only a matter of the right kinds of change in voltage levels, neurotransmitter release is a response to these voltage changes, and so on. Thus, the relevant functional mechanism is only sensitive to voltage differences, and it follows rules that map inputs (and internal states) to outputs.

This is how it is supposed to work. Unfortunately, it does not. Either too many things end up being counted as computational, or we cannot characterize neural systems (or any other natural system) as computational by appealing to the MAC. To see why, we need to go through the details of the MAC more carefully. Let’s start from the bottom and work our way up.

2.1 Rules

According to the MAC, a rule is simply “a map from inputs (and possibly internal states) to outputs” (Piccinini 2015: 121). Importantly, the mapping need not be explicitly represented by the system (either as an algorithm to be followed, or as a set of ordered input-output pairs). However, “it may be given by specifying the relation that ought to obtain between inputs (and possibly internal states) and outputs,” and “it can be defined in terms of any appropriate kind of vehicle” (Piccinini 2015: 122). This is a very broad construal of what counts as a rule, applying to every system that we would generally count as computational, as well as many others.

Figure 2

Figure 2

An impact rotor sprinkler.

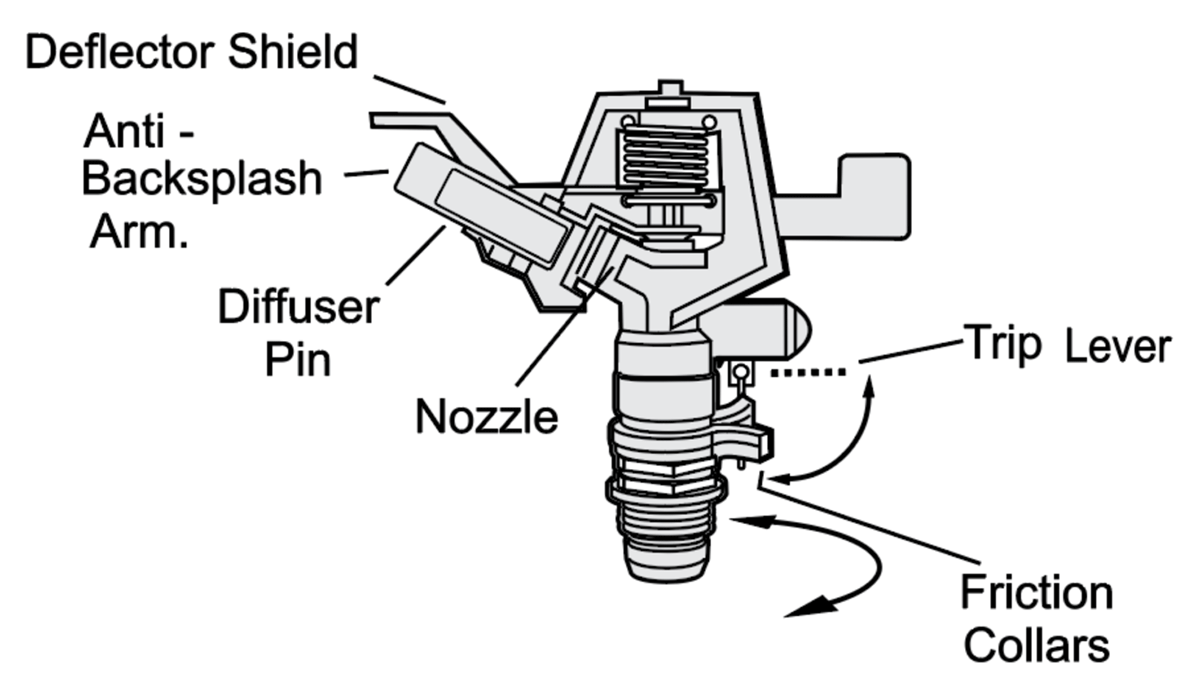
For example, consider the impact rotor sprinkler shown in Figure 2, commonly used to water lawns. This device follows rules in Piccinini’s sense. In particular, it maps inputs and internal states to outputs. The input is liquid at a certain pressure, the internal state is the current position of the nozzle, and the output is liquid at a certain pressure and velocity. The output of this particular sprinkler is (approximately) a periodic step function (in angular degrees) for a given input pressure. Thus, the sprinkler unambiguously satisfies the MAC construal of a rule. Furthermore, it is defined in terms of a kind of vehicle, namely, fluids of a certain viscosity, usually water.⁹ The fact that the sprinkler follows a rule (as do many other things) should not surprising, nor concerning to the MAC, given such a broad conception of what counts as a rule.

Now, there is a subtle problem in the MAC regarding vehicles. Despite how broadly rules are construed, it seems that they must nevertheless be defined in terms of physical quantities or physical properties. It will not do for a rule to be given in terms of unit-free abstractions, such as “low” or “high,” or symbols (even uninterpreted ones) such as “1” and “0.” Rather, the rules have to be defined on something physical, like “five volts” or “in the range of 4.5 and 5.5 volts.” Why? Because rules that are not specified in such a way cannot be processed by a physical, functional mechanism. To do so, we would need an additional ingredient in the MAC, namely, a mapping from the abstract rules to the physically-specified rules (or from abstractly-specified vehicles to physically-specified vehicles), and that additional ingredient is not on offer (and for good reason, given the attention to physical computation). Now, Piccinini does acknowledge that rules specified by non-physical digits or symbols can be understood as abstractions from physical properties, and this move is unproblematic. An example would be specifying that the abstract rule “change a 1 to a 0” can be understood as the concrete rule “change a voltage in the range of 4.5–5.5 V to a voltage in the range of -0.5–0.5 V.”

Despite Piccinini’s claim to the contrary, this elision is quite problematic, which we will see in more detail soon. For now, note that when it comes to natural systems, we want to know whether a system computes, and the MAC is supposed to help us decide. One desideratum of the MAC is “objectivity”: as characterized by the MAC, whether a system computes or not is supposed to be as objective a matter as the sound a heart makes (Piccinini 2015: 141). As such, although we can say that a system designed and built to be a computer may have rules that are “defined” according to abstract vehicles, such as “high” versus “low,” there are no such definitions when it comes to natural systems. We can, of course, ascribe or stipulate mappings between abstractions and physical states however we want; but that is not the road to objectivity.¹⁰ This point becomes clearest when we consider medium-independence.

2.3 A Dilemma

Here is where the MAC faces a dilemma. Recall that the heart of the MAC is the “processing of vehicles by a functional mechanism according to medium-independent rules.” When we carefully look at the relationship between rules and medium-independence, it becomes unclear which is prior.

On one hand, it might work like this. Suppose we determine that a system is governed by rules; given the liberal construal of rules on the MAC, this is an easy step. Next, we discover that those rules display the right kind of sensitivity (i.e., sensitivity with respect to the relevant vehicles). From this, we are to infer that those rules are, in fact, medium-independent. This seems to be the right way to characterize natural systems as computational.

On the other hand, it might work like this. Suppose we already have rules that are defined in a medium-independent way, as is the case with the rules characterizing various abstract automata. From this, it follows that the rules governing the physical system must have the right kind of sensitivity (again, with respect to the relevant vehicles). This seems to be the right way to characterize artificial systems as computational

Unfortunately, for the MAC to apply to all physical computational systems (as it purports to do), we have to choose which way to understand the relationship between medium-independence and the relevant rules. In short: do the rules give us medium-independence, or does medium-independence give us the rules? Unfortunately, neither option is appealing. On the first option, too many things end up being characterized as computation, by the MAC’s own lights. But on the second option, natural systems can never be characterized as computational by the MAC.

This is a subtle point, and one that goes unrecognized in the exegesis of the MAC. We will go through each prong of this dilemma in more detail, walking through an example of the problem for each. For convenience, let us give labels to each prong of the dilemma:

Rules-First From the observed sensitivity of the rules governing a physical system, infer medium-independence.

MI-First Medium-independence is provided by definition, implying that rules must have sensitivity of the right kind as they apply to the physical system.

Let us start with Rules-First. We saw in the previous section some attempts to justify the claim that neural spikes are medium-independent, and that neural systems are thus computational. Now, neural systems do not come with definitions of the rules they follow (neuroscience would be so much easier if they did), much less definitions that dictate that those rules are medium-independent. The rules followed by the system are determined by empirical investigation, and then we can infer medium-independence if the rules have the right kind of sensitivity. This is the idea suggested in the quotations above from Piccinini and Bahar (2013: 462), which just is Rules-First. So far, so good.

Figure 3

Figure 3

A cylinder lock.

Consider now a cylinder lock, illustrated in Figure 3. These locks work by preventing the cylinder from turning (i.e., being locked) unless all of the pins are in a particular alignment. What puts them in that alignment is the pattern of different heights of a key. The right heights, in the right order, move the pins so that they are in line with the cylinder, allowing it to turn, which allows the lock to open (or to be locked if it is already open). We can take the input to be a pattern of heights, the internal state to be the setting of the pins, and the output to be a binary, lock-or-unlock state.¹² We have rules; are the vehicles medium-independent?

Yes, clearly, because the rule from inputs to outputs is sensitive only to differences in key-height, and not to any other property (remember the broad construal of “rule”). Keys can be made of different materials, with different colors, with different temperatures…all that matters is the sequence of heights.¹³ Key-heights are definitely vehicles (i.e., physical states), and cylinder locks have the teleological function to process these vehicles. Putting it all together, cylinder locks are mechanisms with the teleological function to process these vehicles according to this medium-independent rule. Therefore, cylinder locks are physical computing systems.

An immediate objection might be that locks do not have the teleological function to perform computations, so obviously they are not computational! This is true in an everyday sense (which is why it’s being used as a counterexample), but not according to the MAC. Remember, the MAC does not simply stop at saying that physical computing systems are those systems with the function of computing—to do no more than that would be rather vacuous. Instead, the MAC goes on to precisely specify what computation is, and say that physical computing systems are the systems that have the function to do that. Thus, the reply to this objection is simply to note that when we follow the MAC’s specification of computation, it turns out that cylinder locks do have the function of computing.

Now, if cylinder locks process medium-independent vehicles, so do very many other artifacts and natural systems. Not all of them, to be sure, but many, including gear-shifting mechanisms on bicycles, elevators, torque wrenches, pistols, and the sprinkler mentioned earlier. In each case, there is a rule that is sensitive only to differences between spatiotemporal parts of vehicles along specific dimensions of variation; this is enough for medium-independence, and it follows that the system is computational. This characterization does allow that digital computers and neural systems are also computational, but that is not very interesting if so many other things are, too. By Piccinini’s own lights (Piccinini 2015: 145), this is not an acceptable result: the MAC should not count the wrong things as computing, and this is a lot of wrong things.

The way to escape this result is to go with the other prong of the dilemma: MI-First. Piccinini mentions rules that are “defined” by a computation at various points in the discussion of the MAC, which we saw above. This works perfectly when trying to correctly capture artificial physical computing systems, such as digital computers. In these cases, we need not rely only on empirical investigation to know what the relevant rules are. We know what they are by the definition of those rules; following those rules is the raison d’être of such systems in the first place. By definition, the rules given in computational descriptions make no reference to anything physical at all:¹⁴ insofar as computational descriptions are taken to be abstract automata, they cannot refer to anything physical, or else they would not be abstract automata. Because digital computers are implementations of abstract automata, and the rules are medium-independent by definition, we know that any implementation must use rules with only a certain kind of sensitivity with respect to the vehicles being processed. And here we have MI-First.

The problem is one we already saw: natural systems do not come with definitions of the rules they follow, let alone whether those rules are medium-independent. Neural systems do what they do, and through extraordinary amounts of scientific work, we have a variety of ways to characterize the voltage changes in various parts of different neurons; those characterizations show how neural spikes are rapid changes in voltage, how patterns of neural spikes are produced, and so on. But at no point do we discover a rule, equation, or anything else with a definition attached, such that neuron process medium-independent vehicles because of that definition. Of course, we do characterize neural activity with equations and the like, but those equations are not defined in such a way that demands medium-independence (unlike the case of digital computers). It seems that there is no way a natural system could ever count as a physical computing system, because natural systems never come with rules that have definitions, and are thus never medium-independent.

Of course, we can simply stipulate that a neural system is behaving in a way that corresponds to a medium-independent rule. But that was not the point of the MAC. We were supposed to be able to use the MAC to decide if those behaviors are, in fact, medium-independent, and thus whether the system literally computes (at least on the MI-First interpretation of this part of the MAC). If we can simply stipulate medium independence, then the hard work is done: where we stipulate medium independence, computations are being performed; when we do not, they are not. But then the MAC has not done the job is was supposed to do: we are simply giving computational descriptions, and not determining whether physical systems literally perform computations.

The point here is subtle, and worth repeating. Remember, we are not just trying to use the MAC to justify why a system that we have already decided, via independent reasons (including mere stipulation), is computational. Rather, the MAC is meant to provide criteria that allow us to make the determination that a system is (or is not) computational in the first place. Moreover, we are not trying to determine whether a system can be given a mere computational description, but whether a system literally computes. Very many systems that do not literally perform computations can be given computational descriptions, a point to which Piccinini (and all other parties to these discussions) agree.

In the end, neither Rules-First nor MI-First is acceptable. On Rules-First, too many things count as a computational; on MI-First, natural systems can never count as computational. Given the centrality of medium-independence to the MAC, it is unclear how the MAC can be salvaged from this dilemma.

3. Objections and Replies

How might the proponent of the mechanistic account of computation reply to these examples, and perhaps try to amend the account? Let us look at several options that are not on the table. First, the account is supposed to be general enough that it includes digital computation, analog computation, and possibly other, sui generis species of computation. In order to maintain this generality, we cannot add restrictions on the kinds of vehicles that are allowable. One might think, for example, that a sprinkler does not compute because the fluids that are “processed” by a sprinkler are neither discrete nor digital,¹⁵ but continuous. But continuous vehicles are explicitly allowed on the MAC in order to accompany “analog” computers.¹⁶ So we cannot restrict vehicles in this way.

Second, it might seem that we would want to restrict computational systems to those that explicitly follow rules, rather than merely act in accordance with them. However, that would exclude many natural systems that we might want to count as computational—another desideratum of any reasonable account of computation. Neural systems, for example, may well act in accordance with rules, even though these rules are not explicitly represented “in” the neurons.¹⁷ Furthermore, many examples of both digital and analog computers are not stored-program computers, but in a sense “hard-wired” to do what they do, and thus fall on the side of being rule governed rather than rule following. Nevertheless, these are paradigmatic computational systems. We cannot use rule following versus governance as a mark of the computational.

Third, we cannot lift the restriction that computational systems are only those systems that have a particular function (namely, the function of computing). Again, as Piccinini rightly notes, we can give a computational description of virtually anything we want; hence the utility of computational simulations of, say, hurricanes and galaxies. However, the fact that a system can be computationally described or simulated does not warrant any claims about the simulated system literally performing computations. Hurricanes and galaxies do not have the function of computing, so they are not supposed to count as computers. Without the restriction that a system has the function of computing—and not just that the system is computationally describable—too many things will count as computational.

The only thing left is to object to the claim that the rules that things like sprinklers and cylinder locks follow (and the vehicles they operate on) really count as medium-independent. Note first that there is something right about the importance of medium-independence to computation: it is true that computation is, in some sense, medium-independent.¹⁸ A single computational system can be implemented in many different physical media. Conversely, there is something right about the incompatibility of medium-dependence and computation: it is true that the specification of a particular chemical reaction is medium-dependent, and no reasonable account of computation should count the burning of methane (CH₄ + 2 O₂ → CO₂ + 2 H₂O) as a computation. So, perhaps the MAC proponent can argue that the movement of a fluid is not an instance of the medium-independent processing of a medium-independent vehicle, as would be required if the sprinkler is indeed a physical computing system.

But here’s the problem. Medium-independence is a property of computation when it comes to computer science and mathematics, because the way that computation is characterized in these fields is necessarily abstract. The subject matter of theoretical computer science includes only abstract mathematical entities, such as Turing Machines and various other automata. Furthermore, the various results of theoretical computer science are similarly abstract. That the time complexity of a particular algorithm is O(N log (N)) tells us nothing about the actual time that the algorithm will take. Rather, this tells us it will take a certain number of abstract “steps” as a function of the size of the input, where steps are understood as a series of individual members of a set. Of course, we can use this information to determine the time an algorithm will take to run relative to the actual amount of time a single step takes.¹⁹ Nevertheless, entire theory of computation is simply a branch of mathematics, and like all mathematics, it is devoid of physical content.

However, when we move to a physical computing systems, it is difficult to see how to rule out certain physical processes (like the sprinkler and cylinder lock) while ruling in certain other physical processes (like neural systems and digital computers) according to the MAC’s characterization of medium-independence. A genuine physical computing system is always dependent on some particular medium in some particular way. Abstract automata are not dependent on any physical media whatsoever, and so are completely medium independent; we but when we move to physical systems, we have to weaken what medium-independence could mean. That, of course, is precisely what Piccinini’s account of medium-independence attempts to do: medium-independence is a matter of dependence on some (but not all) spatiotemporal—that is, physical—properties. The unintended consequence is that very many things count as medium-independent, as we have seen in the Rules-First prong of the dilemma above. We can, of course, simply stipulate that some processes are medium-independent and others are not, perhaps because of independently-given definitions of computation. However, we then get the result of the MI-First prong of the dilemma.

Here is yet another way to put this point. The MAC needs to be able to characterize neural systems as computational, but characterize cylinder locks as non-computational. In order to do that, the vehicles processed by neural systems need to be medium-independent, but the vehicles processed by cylinder locks need to be medium-dependent. But remember: medium-independence just requires that not all of the properties of the vehicles are relevant to their processing: for neural systems (by hypothesis), the relevant property is voltage, but not color, temperature, etc. However, this is also true of the cylinder locks: the relevant property is height, but not color, temperature, etc. There is no criterion by which we can say the one system does, but the other does not, use medium-independent vehicles.

A more interesting example (at least given the extant dialectic of what does and does not count as a computing system) is the Watt governor, made famous by van Gelder (1995). According to the MAC, this device is an example of something that is not computational, but simply a control system. The reason given is (again) puzzling, because it has to do at least in part with transduction: “a system may exert feedback control functions without ever transducing the signals into an internal medium solely devoted to computing—that is, without any medium-independent processing” (Piccinini & Bahar 2013: 458).

We will set aside the issue of transduction for now, because that is not part of the official, explicated version of the MAC.²⁰ Does the Watt governor follow rules in the generic sense of the mechanistic account of computation? Yes, and that much is easy, as we have seen. Are the vehicles medium-independent? Yes, because the rule that maps inputs to outputs only has to do with the rotational speed or angle of the different components of the mechanism, and not their temperature, color, or chemical composition. If the claim that neural systems are medium-independent is justified by appealing to the Hodgkin-Huxley equations describing voltage change (where it is, specifically, voltage that is supposed to be the medium-independent vehicle), then the claim that the Watt governor is medium-independent must also be justified by appealing to the equations describing its angle and rotation (where it is, specifically, angle and rotation that are the medium-independent vehicles).

Perhaps another way to defend the MAC is to focus on the function of the mechanism in question. The work of restricting which rules count is, it seems, supposed to be done by the requirement that the system in question has a particular function. Raindrops collected in a pothole may also follow a medium-independent rule, but there is no computation in sight because potholes collecting rain do not have teleological functions.²¹

Unfortunately for the MAC, however, the sprinkler and the Watt governor do have the function of processing their (according to the MAC) medium-independent vehicles according to rules. Although rule-following is easy, satisfying the functional requirement is more difficult, because many physical processes are not the result of the action of a functional mechanism. However, many functional mechanisms act on vehicles in such a way that only some spatiotemporal properties of those vehicles (and not others) are relevant to the input-output behavior of the mechanism. Again, it would be too much to say that everything does (e.g., specific chemical reactions are probably counterexamples). But many functional mechanisms are medium-independent in just the way the MAC requires (e.g., torque wrenches, lamps, sprinklers, cylinder locks, and a whole host of other artifacts), and thus count as physical computing systems.

Finally, a proponent of the MAC might argue that some physical computational systems (or at least some programs), such as compilers, parsers, and sorters, do not process representations.²² Given that accounts of computation that rely on representations cannot accommodate these clear (and core) examples of computation, we ought to adopt the MAC. However, upon closer inspection, these programs must process representations, or else they would not be compilers, parsers, or sorters.

Consider a compiler. At a very abstract level, compilers simply take a set of strings as input and produce as output another set of strings (this is what all software does, considered abstractly enough). More concretely, however, compilers take code written in a high-level language and produce assembly code: crucially, however, those strings are representations. An input string, such as

printf(“Hello, world!\n”);

represents an instruction in the high-level programming language C; the corresponding lines of assembly code produced as output represent instructions for the relevant instruction set architecture. If the input and output did not represent instructions, then this would simply not be a compiler.²³

Now one might worry that these are not representations of the right type, because they represent states or commands internal to a particular computing system, rather than something external. Considered very loosely, even abstract automata have states that “represent,” because they must refer to other states within the system, and the MAC allows for this minimal type of representation. But this would be a misunderstanding of how compilers (and similar programs) work. A compiler running on computer A can take as input code written on computer B, and produce assembly code for computer C. There is nothing that requires the input to represent anything internal to the system itself. The output must refer to states and instructions in some type of system, but nothing requires that those states and instructions are the very ones on which a compiler is running. The compiler that takes the C++ string above as input certainly does not, itself, need to have the command to print the string “Hello, world!”

Space prohibits further elaboration, but similar points can be made about parsers and sorters as well. In the main, however, even if we assume that there are a few cases that the MAC correctly classifies where other accounts fail, there are still many other cases (torque wrenches, sprinklers, cylinder locks, etc.) that the MAC fails where others get it right. Until the latter problems are solved, this is not a point at which the MAC’s benefits outweigh its drawbacks.

4. Sketching a Way Forward

It may well be that a successful philosophical account of computation counts—or does not count—certain things as computational systems in unintuitive ways. If the account is otherwise satisfactory, then the occasional clash with intuition is the price we pay for progress. However, the price to pay for adopting the MAC is much too high, because of the dilemma mentioned in Section 2.3. My own view is that the orthodoxy is largely correct, but needs some additional work. In short, a version of the orthodox view—that representation is necessary for computation—allows us to articulate exactly why the sprinkler is not a physical computing system: it is not a computing system because it does not process representations. However, in the right context, this kind of mechanism could be a computing system, if its vehicles were, in fact, representations. Moreover, Piccinini is correct to focus on mechanisms; we simply need to couple a version of the mechanistic view with a version of the orthodox view. Fully developing this account will have to wait for another day, and Shagrir (2022) has offered an excellent defense of a version of the orthodox view in light of challenges from competitors (including Piccinini). Here I will mention a few of my own points that I hope to develop in future work.

What unifies physical computing systems of all kinds is that they are mechanisms: Piccinini has done the field a great service by articulating this point. Although we cannot characterize computational systems correctly without appealing to representations, we can couple the mechanistic view with a version of a semantic view to yield what I will call (for now) the representational view. On this view, physical computing systems are those systems with mechanisms that process physical representations, where the mechanism is sensitive only to the properties of the representations that are responsible for doing the representing. In digital computers, for example, it is the voltage of circuit elements that does the representing, so the mechanism doing the processing must be only sensitive to voltage (and not temperature, color, mass, etc.). In a neural system, the mechanism must be sensitive only to whatever the relevant property happens to be (e.g., voltage change).

This view will face many of the challenges that semantic views face. One challenge is to provide a satisfactory account of representation, given the heavy lifting that representation does in the account. On the other hand, some version of the semantic view of computation is the one that many psychologists, neuroscientists, and other cognitive scientists take as a starting point. For example, von Eckardt (1993) takes the manipulation of representations to be one of the basic capacities of computation as understood by cognitive science. Koch (1999: 1) states that, when the brain computes, he means that it “takes the incoming sensory data, encodes them into various biophysical variables, such as the membrane potential or neuronal firing rates, and subsequently performs a very large number of ill-specified operations, frequently termed computations, on these variables to extract relevant features from the input.” Perhaps one can interpret the encoding of data in such a way that it does not result in a representation, but I do not see how. A final example is London and Häusser (2005: 504), who state “Brains compute. This means that they process information, creating abstract representations of physical entities and performing operations on this information in order to execute tasks.” Obviously the fact that a variety of researchers endorse a representational view is not a knock-down reason to accept it. But in the absence of a compelling reason to adopt an alternative view, it is prima facie evidence in its favor.

Another challenge is that some things that are supposed to be examples of computational systems do not appear to traffic in representations at all. We mentioned compilers and parsers above, but those are not good examples. Better examples include the many computable functions defined with respect only to an alphabet that has no associated representation; showing that a given function is computable using such an alphabet, relative to some particular type of automaton, is standard fare in virtually every computability theory textbook. As such, there are many abstract automata that do nothing more than turn a meaningless (but well-defined) string of symbols into some other meaningless (but well-defined) string of symbols. If such a system is physically implemented, mechanistic accounts would count it as computational, whereas semantic accounts would not. In fact, Piccinini uses the Turing Machine as a paradigm example of a computational system. The vast majority of Turing Machines do not traffic in anything representational; they simply compute a computable function. Although classifying Turing Machines as computational seems to be a point in favor of the MAC (and against semantic views, which do not classify them as such), this is a mistake, due to a subtle confusion between computability and (physical) computation.

There is enough to say about this point to fill at least another essay; a sketch will have to do for now. To put it simply, my own solution, as well as that offered by Shagrir (2022), is to bite the bullet and claim that not everything that is a physical implementation of an abstract automaton (such as a Turing Machine) is a computational system. Rather, only those physical systems that process representations are candidates for computational systems (and only those systems that process representations in the right way actually are computational systems). Moreover, it is simply a category mistake to think that Turing Machines themselves are computational systems; Turing Machines (and all other abstract automata) are abstract mathematical objects that cannot do anything at all, let alone compute. Setting that aside, physically implementing an abstract automaton does not guarantee that you get a computational system: for that, you need the system to traffic in representations, too (Shagrir 2022).

In brief, the reason for this is that I take it to be a conceptual fact about computation that every computation is a computation of something, where the “of something” is defined in terms of representations and how they are processed. Historically, this is what was meant by computation as performed by human computers, the very people whose activity the Turing Machine was meant to model. Interestingly, the Turing Machine does many things which are “computable,” but, if done by a human, would never have counted as computations (or the result of computations). For example, although a person could systematically manipulate meaningless strings of meaningless symbols into different meaningless strings of meaningless symbols—similar to how many computable functions are defined—there is nothing that this activity would be a computation of. A person engaged in this activity would not be computing anything at all. Computing machines—both digital and analog, from abaci and the Antikythera mechanism to contemporary digital computers—were explicitly created to manipulate representations. Using a computing machine just meant using a machine to manipulate representations in ways that are faster and more accurate than what a person could do alone.

As it turned out, studying Turing’s mathematical model of what a human computer could do (as well as other models of computation, such as the work of Church [1936], Post [1936], and many others) became quite interesting in its own right as a branch of mathematics. In a real sense, the class of things that a Turing Machine could “compute” (i.e., the computable functions) outstrips the class of things that would count as performing a computation were a human to do them. In short, there are many computable functions that, if physically implemented, would not be computations. This is not as absurd as it sounds, given that “computable” is a mathematical predicate, applicable to certain mathematical functions, and “computation” is an activity that existed long before any particular mathematical model of that activity, including Turing Machines or any other automata. Again, however, the full view must wait for another time.

At the same time, certain types of computation, such as analog computation, are simply not amenable to analysis via Turing Machine (or other abstract automata). The MAC is intended to capture analog computation, but fails to do so. Like most discussions of analog computation, Piccinini (2015) takes analog computers to be distinguished by their use of continuous variables; however, analog computers often used discrete variables, yet were distinct from digital computers (Maley, 2023). The right way to characterize analog computers is via their use of analog representation; a distinction between continuous and discrete is not sufficient (Maley 2011). Of course, appealing to representational types is not an option for the MAC. But for the representational account sketched here, this is quite straightforward.

Even worse for the MAC is that many analog computing elements are functionally identical to other mechanical and electronic components in non-computing systems, but are distinguished by the fact that in one context they manipulate representations, and in another they do not. For example, differential gears have been used in virtually all automobiles for more than a century, as well as in many industrial contexts. In cars and trucks, these gears allow drive wheels on opposite sides of the vehicle to rotate at different speeds while the vehicle turns. But in mechanical analog computers, these devices were used to perform arithmetic operations on variables.

The MAC does not have the resources to correctly characterize this part of a mechanical analog computer while not simultaneously counting all mechanical differential gears as computing, unless we have already independently stipulated that one is a computer and one is not (i.e., the MI-First prong of the dilemma). Just as with the example of the cylinder lock, this device is a mechanism that is sensitive to only one property of its vehicles (thus medium-independent), operating according to a rule, and it has the function of doing exactly that. Similarly for analog computers. The only difference is that in analog computers, the rotation represents the value of a variable, but in other applications, the rotation does not represent anything at all. Again, this is a simple matter to capture on the representational account.

More generally, the representational account classifies types of computation according to types of representation. Digital computers are digital because they use digital representations; analog because they use analog; and perhaps other types of computers are something else entirely because they use entirely different types of representation.

Now, one might worry, as articulated in Piccinini (2004: 377), that accounts of computation that rely on representations must have a non-representational way of individuating computational states. The concern is that without such a non-representational individuation procedure, there is a circularity: the contents of mental representations are explained by computational relations among those representations, but computational relations are individuated by the contents of computational states.²⁴ However, Shagrir (2022: 197) notes that this circularity is only a problem if the contents of computational states are individuated the same across all computational systems, and one need not be committed to that view. Shagrir and I agree on the general point that we should be pluralists about semantic content or representation: neuroscientists may have one view of what counts as a representation and what gives them their content, computer scientists another, psychologists another, and so on. Even researchers within those fields may have differing standards, depending on their interests.

Although the MAC does not work as an account of physical computation, it succeeds insofar as it points out the necessity of functional mechanisms for such an account. What unifies computation in natural and artificial systems, and in digital and analog systems, is the presence of mechanisms. However, without appealing to the manipulation of representations, the MAC counts as computational very many things that it should not. The way to fix the account may be to marry the MAC with some kind of semantic account of computation, along the lines of that developed by Shagrir (2022). Developing this representational account of computation, only briefly sketched here, is a task for future work.

5. Conclusion

The mechanistic account of computation fails as a unified philosophical account of computation because of a dilemma having to do with medium-independence at the heart of the account. Either too many things (by the MAC’s own lights) are characterized as computational, or it cannot count natural systems as computational without some separate, independent attribution of (and justification for) medium-independence already in place. Nevertheless, the mechanistic account of computation makes significant progress toward articulating an important and necessary feature of physical computational systems; namely, the presence of the right kind of mechanism. By coupling this part of the mechanistic account with a version of a semantic account, we can develop a new account of physical computation that prioritizes physical representations. But that story is a longer one to tell, and must wait for another day.