The annual Forbes magazine’s lists of the wealthiest individuals in the world are a widely used source of data about the dynamics of wealth concentration. Together with other similar compilations (such as those published by Bloomberg, Hurun Rich List in China, Manager Magazin in Germany, and Wprost in Poland), they offer a window onto the forces contributing to the concentration of top-end wealth, including the effects of macro-economic shocks, political and market factors, globalization, and technology (for example, see Freund & Oliver, 2016). They complement the estimates of global and national wealth concentration published annually by Credit Suisse Bank and those published by the World Inequality Database (WID). The WID data and Credit Suisse global wealth reports provide annual estimates of concentration of wealth by country and globally.
Both sources enable analysis of the dynamics of wealth accumulation. The Forbes lists, moreover, permit examination of the distribution of top-end wealth at any one time, albeit for a very small segment of the wealthiest. The wealthiest 400 individuals in the United States, for example, represent approximately 0.00025% of families, or one in 200,000, although they own around 3.2% of aggregate wealth.1 Combining the two sources allows comparison between the dynamics of wealth accumulation of the very wealthiest and the growth of wealth for the top 1% or top decile and analysis of the relationship between macro-level and micro-level wealth accumulation. Because the Forbes lists provide estimates of the net wealth of each individual listed, we analyze the distribution of top-end wealth. Specifically, we can measure how closely the function approximates a pure Pareto curve. This is useful because variations in the shape of the distribution—called the “signature” of the curve—reveal differences in the processes by which wealth is generated and dissipated.
The goal of this paper is to assess the degree to which political–institutional forces as opposed to market forces shape the process of wealth accumulation. I exploit variation across countries and over time to explore factors associated with aggregate and individual wealth accumulation.
Aggregate and Individual Wealth Accumulation
Because estimates of wealth shares tell us only the total value of total household wealth held by all individuals (or families) exceeding some threshold relative to national wealth—such as the share of total wealth owned by the wealthiest 1% of the population—they cannot say anything about the composition of that group or changes from year to year. They do not indicate the degree of stability or turnover from one year to the next. Moreover, the threshold rises or falls from year to year as the number of people with high wealth increases or decreases. For example, the cutoff point to qualify for the top 1% of wealth in the Saez–Zucman dataset has risen from $1.9 million in 1982 to $3.8 million in 2012 in constant 2010 USD (Saez & Zucman, 2016).2 In the case of the Forbes lists, different thresholds are used—top 400, top 200, or top 100; or all those whose wealth in a given year exceeds US$1 billion.
Even if turnover on the lists from year to year is high, so long as the value of total assets held by those in a given top share increases relative to the aggregate national wealth, the top share will increase. Moreover, if the income thrown off by those assets enables the wealthiest to invest a fixed or rising share portion of the income in more income-generating wealth, their wealth will increase (Stiglitz, 2015).3 Thomas Piketty has demonstrated that the return on wealth can exceed the rate of growth of national income over long periods of time (r > g, in his well-known inequality), driving an increase in the share of capital income in total income over time, in turn leading to a concentration of wealth in fewer hands unless significant wealth destruction or taxation impedes the process (Piketty, 2014).
However, it is of interest to determine how much the composition of a particular group of the wealthiest represents a stable continuity of wealth in particular families (dynastic wealth), as opposed to the entry of new innovative entrepreneurs. How many billionaires are self-made, and how many have inherited their wealth? How many individuals fall off the list from year to year? In general, we assume that higher turnover reflects a more dynamic economy, producing concomitant benefits to the economy as a whole as enterprising individuals take risks to exploit improvements in technologies in production in a competitive market economy. The rents accruing to an entrepreneur whose innovation yields first-mover advantages are generally considered to enhance social welfare. (Often they are called “Schumpeterian” or innovation rent, cf. Jones & Kim, 2018; Mankiw, 2013). On the other hand, continuity of the composition of the wealthiest may reflect a stable oligarchy based on control of land or natural resources. We care, therefore, about the relative balance between accumulation and dissipation of wealth, something only discernible by analyzing the composition of lists from year to year.
Even without making assumptions about how much income represents returns to labor and how much returns to capital, we use the lists to relate the following three processes: the overall growth of household wealth; the growth of wealth concentration; and the growth of wealth of the very wealthiest. Overall, wealth concentration is represented by figures on the top shares, i.e., the share of total wealth held by the top decile, top 5%, top 1%, top 0.1%, and so on, of all privately held wealth. These figures are reported in the WID project (wid.world) associated with Thomas Piketty and his collaborators as well as by the annual Global Wealth Report figures published by the Credit Suisse Bank.4 The question is: how is the growth of the total wealth of the wealthiest reported in the rich lists related to the concentration of wealth among the top decile or some other segment? If wealth increases proportionally to the size of wealth, then we would expect that the mean wealth at the top would grow faster than the mean wealth in the country.
This turns out to be the case. For the five countries that have the largest number of Forbes’ billionaires in 2021—the United States, China (including Hong Kong), Germany, Russia, and India, the average annual rate of growth for the wealthiest exceeds the average rate of growth in the country by a multiple of 2.5—3.5 times, except in India, where the total wealth of the top forty has grown more slowly than has average wealth in the country. Table 1 shows the results, as well as the WID estimates, for top-end and bottom-half wealth shares using WID, Forbes, and Hurun data.
| Country | CAGR mean wealth | CAGR Forbes wealthiest | Ratio of top share to mean wealth growth | Bottom-half wealth share | Top 1% wealth share | Ratio of top-to-bottom shares |
|---|---|---|---|---|---|---|
| US | 2.43% | 5.79% | 2.38 | 1.51% | 34.87% | 23.9 |
| China | 8.02% | 27.58% | 3.44 | 6.32% | 30.96% | 4.9 |
| India | 4.98% | 0.33 | 0.24 | 5.93% | 33% | 5.56 |
| Germany | 1.82% | 4.5% | 2.47 | 1.825% | 29.68% | 8.86 |
| Russia | 3.19% | 7.22% | 2.27 | 3.19% | 47.73% | 15.25 |
Notes: India is in top forty, 2007–2021; Germany is in top forty-two, 2000–2022; Russia is in top 100, 2004–2020; US is in top 100, 2000–2021; China is in top 100 (Hurun), 2004–2020.
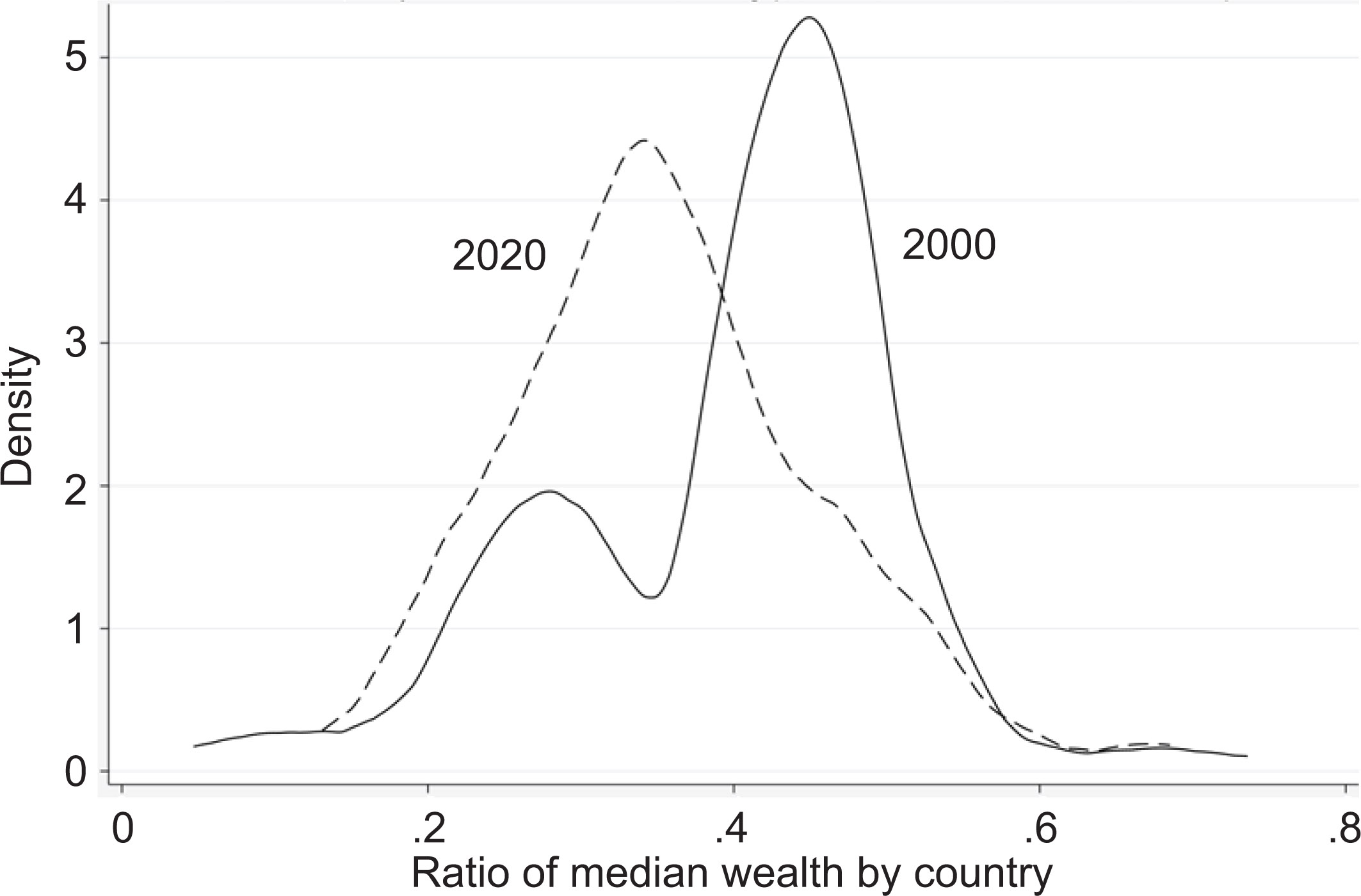
These five countries are chosen because according to the 2021 Forbes list, their citizens comprise the largest share of billionaires globally. However, the concentration of wealth within countries is a global phenomenon. According to the Credit Suisse Global Wealth data books, for the 176 countries for which they collect data, both mean and median wealth per adult rose at a compound average annual rate of about 5.5% from 2000 to 2020. Meanwhile, because mean wealth per adult is so much higher, the overall ratio of median per adult wealth to mean fell from 39.7 to 34.8.
Figure 1 indicates the distribution of countries by the median: mean ratio, comparing 2000 and 2020. In 2000, the most frequent pattern in countries was for the median adult’s wealth to range between 40% and 50% of the mean. By 2020, in the great majority of countries, median wealth was less than 40% of the mean. This means that in more and more countries, wealth became more concentrated.
Source: https://www.credit-suisse.com/about-us/en/reports-research/global-wealth-report.html
Across the world’s countries, median per capita wealth has fallen behind mean wealth as global wealth has grown more concentrated over the past 20 years, both within and between countries. If we take countries as units, the Gini index for wealth per capita fell slightly, from seventy-five in 2000 to seventy in 2020, and the median: mean ratio of wealth rose slightly. However, the greatest increase in wealth inequality has occurred within countries. This is observed in the fact that the gap between mean and median wealth grew in many more countries as wealth accumulated more quickly at the top within countries than between them.
How does this compare with increase in the wealth of the Forbes’ wealthiest individuals? Comparing the 400 wealthiest on the global lists in 2004 and 2020, the compound average growth rate (CAGR) for the total wealth of the group (and for the average wealth of each member) was 9.5%. Even discounting for inflation, the wealthiest saw a far greater increase in their net wealth than did their countries as a whole.5
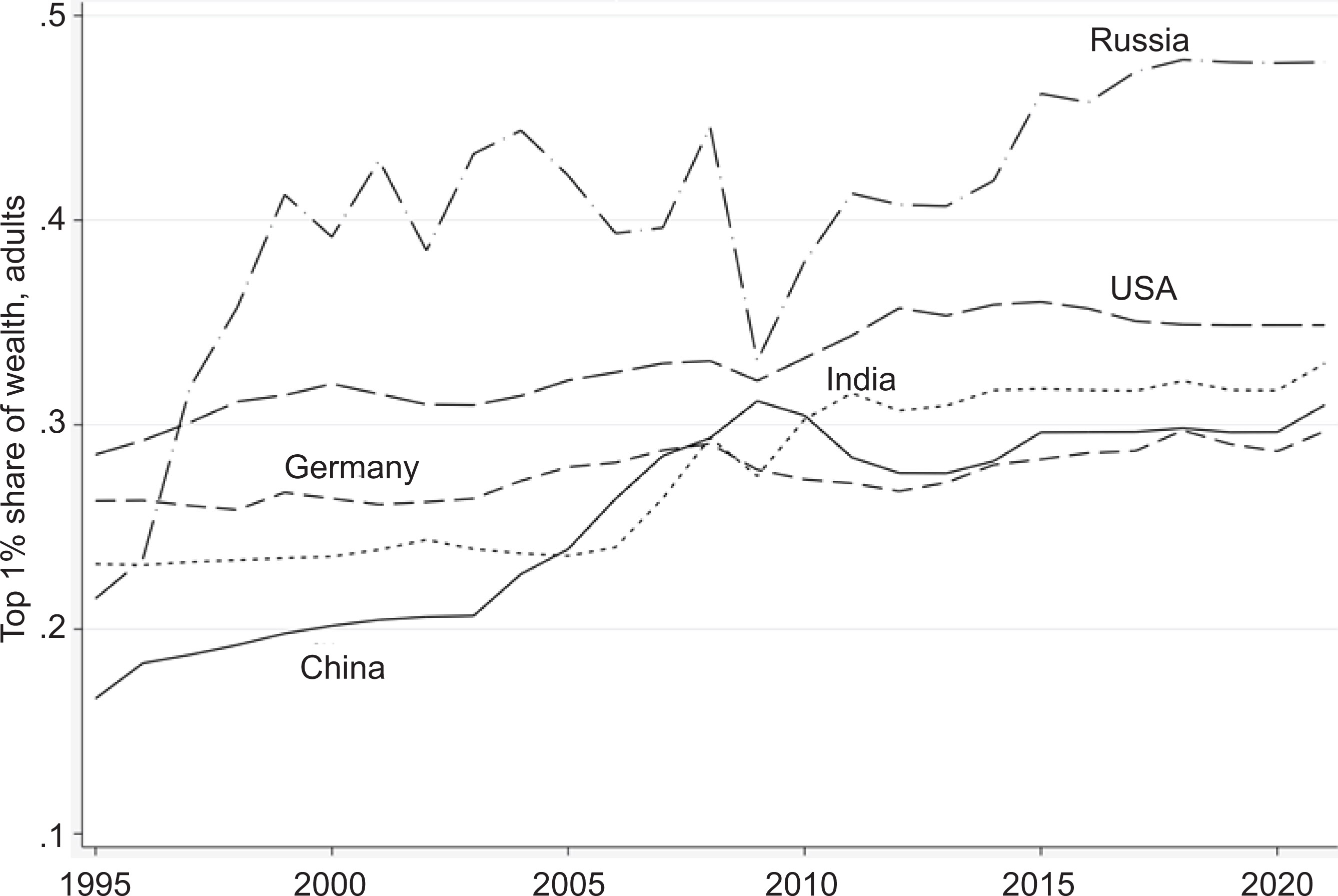
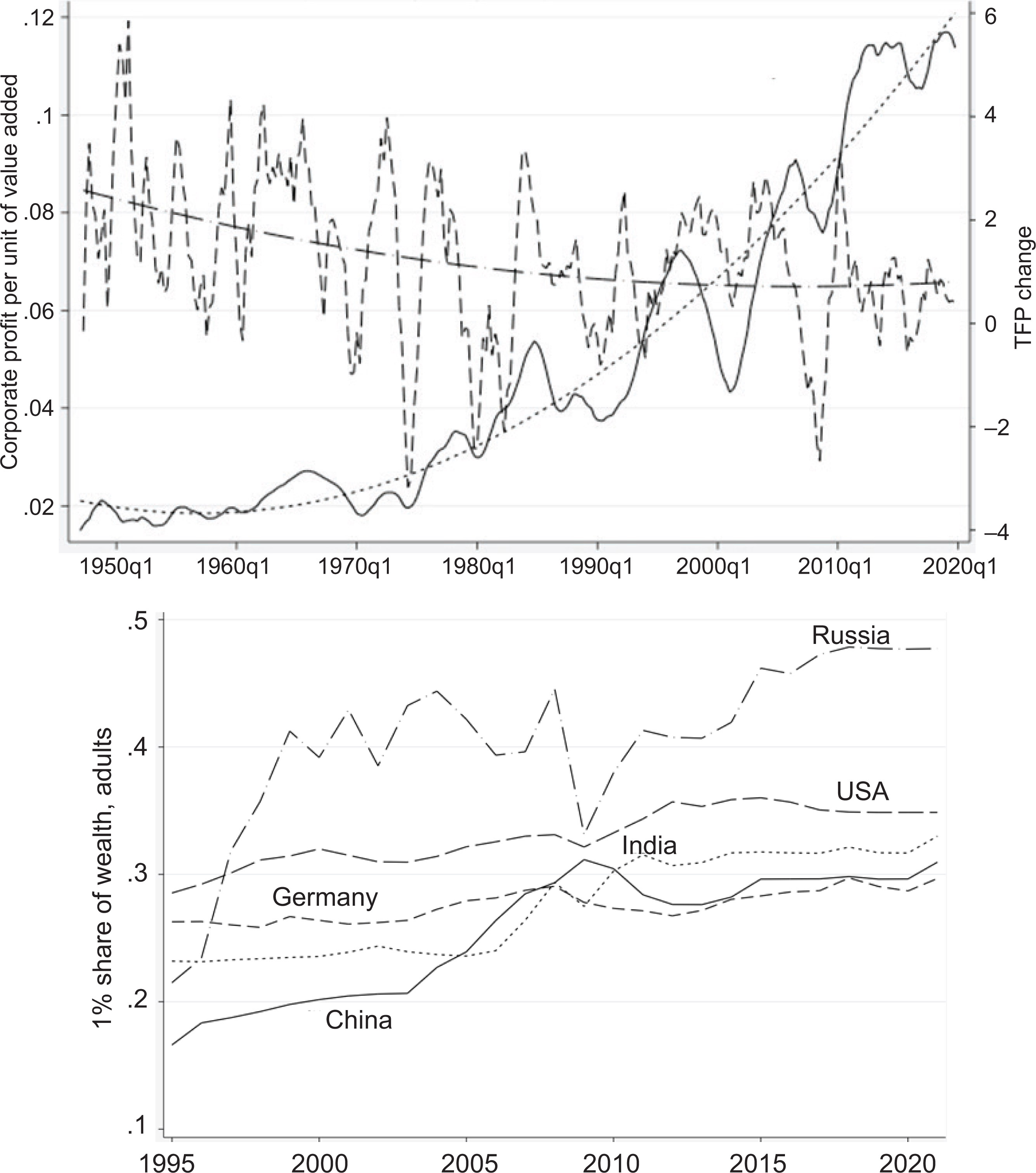
Differences in policies and institutions account for the significant differences in the growth trajectories of wealth distribution. Compare the WID world wealth distribution data for the years 1995–2021 for the United States, European Union (EU), Germany, the United Kingdom, France, Canada, Russia, and China. These countries are chosen to represent market-oriented economies and two transition countries, all exposed to similar trends in world economic technology change and product markets. Figure 2 shows change in the share of wealth held by the top 1% of individuals. Over this period, Russia, China, and the United States experienced a significant increase in the top 1% share. Meanwhile the EU as a whole, Canada and the United Kingdom saw little change, whereas France’s top and bottom shares were slightly more volatile.
Individual-level analysis of the continuity of wealth among those listed in the Forbes’ global wealthiest lists confirms that the greater an individual’s net worth in a given year, the more likely the individual is to realize an increase in net worth in the following year. Table 2 presents the results of a simple panel regression in which the individual–year is taken as the unit of observation. A given individual’s wealth in a given year is modeled as a function of the same individual’s wealth in the prior year and the passage of time. The individual wealth in a given year is the dependent variable; the one-year lagged value of wealth and time is on the right-hand side. Fixed effects are used to hold constant the characteristics of each individual. The coefficients for the lagged variable’s effect are given in bold-face.
| Worth_ | Coef. | St. Err. | t–value | p–value | 95% Conf | Interval | Sig |
|---|---|---|---|---|---|---|---|
| Full list (N = 1,278) | |||||||
| Year | 0.121 | 0.02 | 6.13 | 0 | 0.083 | 0.16 | *** |
| L | 0.921 | 0.014 | 66.00 | 0 | 0.894 | 0.949 | *** |
| Constant | –242.831 | 39.812 | –6.10 | 0 | –320.883 | –164.779 | *** |
| Mean dependent var | 9.668 | SD–dependent var | 10.959 | ||||
| R2 | 0.583 | Number of obs | 5,318 | ||||
| F-test | 3105.142 | Prob > F | 0.000 | ||||
| Akaike crit. (AIC) | 29520.569 | Bayesian crit. (BIC) | 29540.305 | ||||
| Top 100 | |||||||
| Year | 0.313 | 0.073 | 4.29 | 0 | 0.17 | 0.457 | *** |
| L | 0.943 | 0.031 | 30.44 | 0 | 0.882 | 1.004 | *** |
| Constant | –627.108 | 146.717 | –4.27 | 0 | –914.983 | –339.233 | *** |
| Mean dependent var | 20.993 | SD-dependent var | 16.626 | ||||
| R2 | 0.612 | Number of obs | 1,329 | ||||
| F–test | 872.642 | Prob > F | 0.000 | ||||
| Akaike crit. (AIC) | 8756.600 | Bayesian crit. (BIC) | 8772.176 | ||||
| Top 101–200 | |||||||
| Year | 0.364 | 0.028 | 13.19 | 0 | 0.31 | 0.418 | *** |
| L | 0.232 | 0.044 | 5.23 | 0 | 0.145 | 0.32 | *** |
| Constant | –726.497 | 55.283 | –13.14 | 0 | –835.052 | –617.942 | *** |
| Mean-dependent var | 7.469 | SD-dependent var | 2.667 | ||||
| R2 | 0.550 | Number of obs | 957 | ||||
| F–test | 396.319 | Prob > F | 0.000 | ||||
| Akaike crit. (AIC) | 2913.817 | Bayesian crit. (BIC) | 2928.408 | ||||
| Top 201–300 | |||||||
| Year | 0.36 | 0.021 | 17.11 | 0 | 0.318 | 0.401 | *** |
| L | –0.133 | 0.057 | –2.36 | 0.019 | –0.245 | –0.022 | *** |
| Constant | –718.105 | 42.097 | –17.06 | 0 | –800.869 | –635.342 | *** |
| Mean–dependent var | 4.783 | SD-dependent var | 1.579 | ||||
| R2 | 0.613 | Number of obs | 731 | ||||
| F–test | 312.276 | Prob > F | 0.000 | ||||
| Akaike crit. (AIC) | 877.044 | Bayesian crit. (BIC) | 890.827 | ||||
| Top 301–400 | |||||||
| Year | 0.309 | 0.023 | 13.17 | 0 | 0.263 | 0.355 | *** |
| L | –0.122 | 0.08 | –1.53 | 0.127 | –0.279 | 0.035 | |
| Constant | –618.058 | 47.01 | –13.15 | 0 | –710.675 | –525.441 | *** |
| Mean-dependent var | 3.682 | SD-dependent var | 1.317 | ||||
| R2 | 0.680 | Number of obs | 550 | ||||
| F-test | 248.567 | Prob > F | 0.000 | ||||
| Akaike crit. (AIC) | 259.086 | Bayesian crit. (BIC) | 272.016 | ||||
***p < 0.01,
**p < 0.05,
*p < 0.1.
The results are striking. Overall, continuity in the levels of wealth from year to year is extremely high (the regression coefficient for the entire set of unique individuals is 0.921). However, for the top 100 individuals, the coefficient is much stronger than for individuals at lower ranks. It is 0.943 for the top 100 individuals, falling to 0.232 for the next 100, and turning negative for the bottom two groups of 100. In other words, having greater wealth in a given year increases the likelihood of increasing it in the next year. This finding further indicates that wealth accumulates at a rate proportional to the level of wealth.
The Distribution of Wealth at the Top
The Forbes lists permit us to analyze the distribution of wealth at the individual level (something that wealth shares data do not allow). Economists since Vilfredo Pareto have discovered that in many cases, top-end wealth distribution follows a distinctive power law pattern; since then, one generally referred to as the “Pareto distribution.” In the Pareto distribution, the slope of the curve relating the log of the rank of the wealth of the wealthiest to the log of the wealth is close to 1. This coefficient is commonly referred to as α. The α coefficient is interpreted as an inverse measure of the concentration of wealth (or incomes) at the top-end of the distribution. That is, the higher the rank, the smaller the number of people with wealth at that level. Therefore, the smaller the value of α, the steeper the slope or gradient of inequality at the top and the more quickly the cumulative distribution of frequencies reaches 1.
An enormous amount of research since Pareto has gone into discovering how many real-world economies follow this pattern. The consensus appears to be that a surprisingly large number of economies do show a Pareto distribution for incomes and wealth above a certain threshold; below that threshold, the Pareto distribution breaks down. The particular threshold varies by time and place and, in some cases, at different levels of the distribution at the top. Moreover, contrary to Pareto’s conclusion, the Pareto coefficient itself is different in different societies at different times, and sometimes even for different segments of the top-end of the distribution in the same society. Nevertheless, Pareto’s discovery has continued to puzzle economists ever since: many of the processes that generate income and wealth inequality are linear and additive, but they yield a multiplicative effect. Then, why do we observe such extreme inequality of incomes at the very top for people who are alike with respect to levels of education, experience, social connections, talent, and other measurable attributes? There is still no good answer to this question, but there has been no shortage of ingenious efforts to devise models to explain it that are consistent with neo-classical assumptions about how labor markets work (cf. Armour, Burkhauser & Larrimore, 2016; Atkinson, 2017; Atkinson, Piketty, & Saez, 2011; Brzezinski, 2014; Price & Edwards, 2020; Gabaix, 1999; Krugman, 1996; Strogatz, 2009).
Pareto distributions are used to describe the structure of inequality among a group of high-wealth individuals at a given point in time. However, any given distribution is the outcome of a process of continuous accumulation and dissipation of wealth. What type of process could explain the pattern of distribution of wealth observed in the rich lists?
One model that describes a related process is attributed to Udny Yule, who analyzed growth in a number of biological species and genera over time (Newman, 2005). In Yule’s model, growth is proportional to some characteristics of each member of a set of members, such as the number of species in a genus and the number of genera, the wealth of individuals in a population, the size of population in cities (the number of citations to a published article), and many other phenomena in natural and social worlds. Applied to growth and distribution of income and wealth, the model would assume that at some given time there is a set of families with a given distribution of income and wealth. Over time, inequality of incomes among them increases, for several reasons. First, levels of earnings diverge. Those with higher earnings realize higher income growth. That is, the growth of income is proportional to the size of income, much in the way that published articles with more citations tend to attract still more citations, and a populous city tends to attract more new residents. Why should growth of earnings be proportional to level of earnings? Both market-related changes (e.g., globalization and skill-biased technological change) and political changes (such as weakening of workers’ bargaining power) play a part. Second, structure of the labor market changes. Fewer families occupy the middle range of earning levels because more families live below the middle range or above it. Third, there is a recursive relation between income and wealth: those with higher incomes invest a greater share of their income in assets that in turn yield more income. In addition, investors with more capital have more opportunity to realize higher rates of return. At the same time, some of the individuals who had extremely high levels of income or wealth fall out of the group; some suffer severe market losses or political misfortune, others divide their estates among multiple heirs or donate everything to worthy causes. The rate of growth or decline in the share of income and wealth of the top group is governed by the ratio of the rate of gains to the rate of losses among those in the group, that is, the ratio of accumulation to dissipation.
Therefore, unless strong competition or government tax policies restrain the rate of wealth accumulation, income and wealth form a recursive relationship. We illustrate this point as follows:
At any given time, there is a set of individuals with a given distribution of income and wealth. If over time, inequality of income among them increases, wealth also increases, because those with higher incomes tend to save, and invest, a higher share of their income. Since some wealth throws off income, a portion of which is reinvested in income-producing wealth, and since more high-yielding investments are available to those with more to invest, the recursive relationship between wealth and income acts as an accelerant to the accumulation of wealth. So long as the wealth is accumulated at a rate higher than the rate at which it is dissipated, the concentration of wealth will rise (Piketty, 2014).6
In the real world of economic inequality, the rich are hardly passive vessels of the fate of the marketplace. Not only do they save a higher share of their incomes, they also intervene actively to create favorable conditions for the accumulation of income and wealth. Both create a recursive relation between income and wealth. Those with greater income and wealth have greater influence over regulatory and tax policy and deploy it to obtain higher incomes from both labor and capital. For example, in the United States, tax policy has become more favorable to capital income since the late 1970s to the point where for those at the very top, the income tax system is in fact regressive (Saez & Zucman, 2019). Therefore, as those with the highest incomes derive an increasing share of their incomes from investments, they are in turn able to invest a higher share of that income to generate yet more investment income. They also reproduce their material and social advantages across generations (Collins, 2021). Then the proportional growth of income and wealth at the top represents a combination of exponentials. Accumulation of income and wealth at the top outpaces its dissipation.
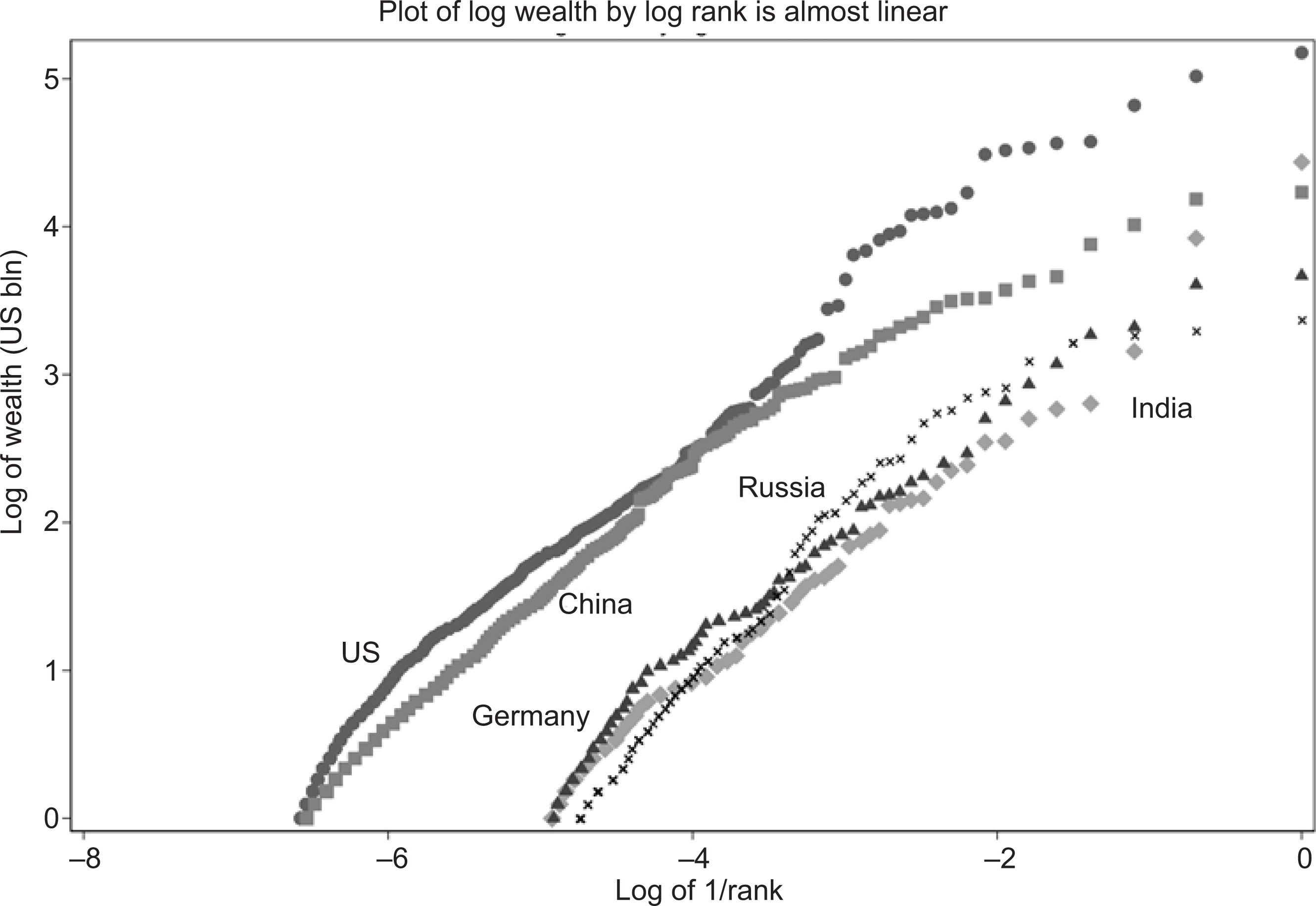
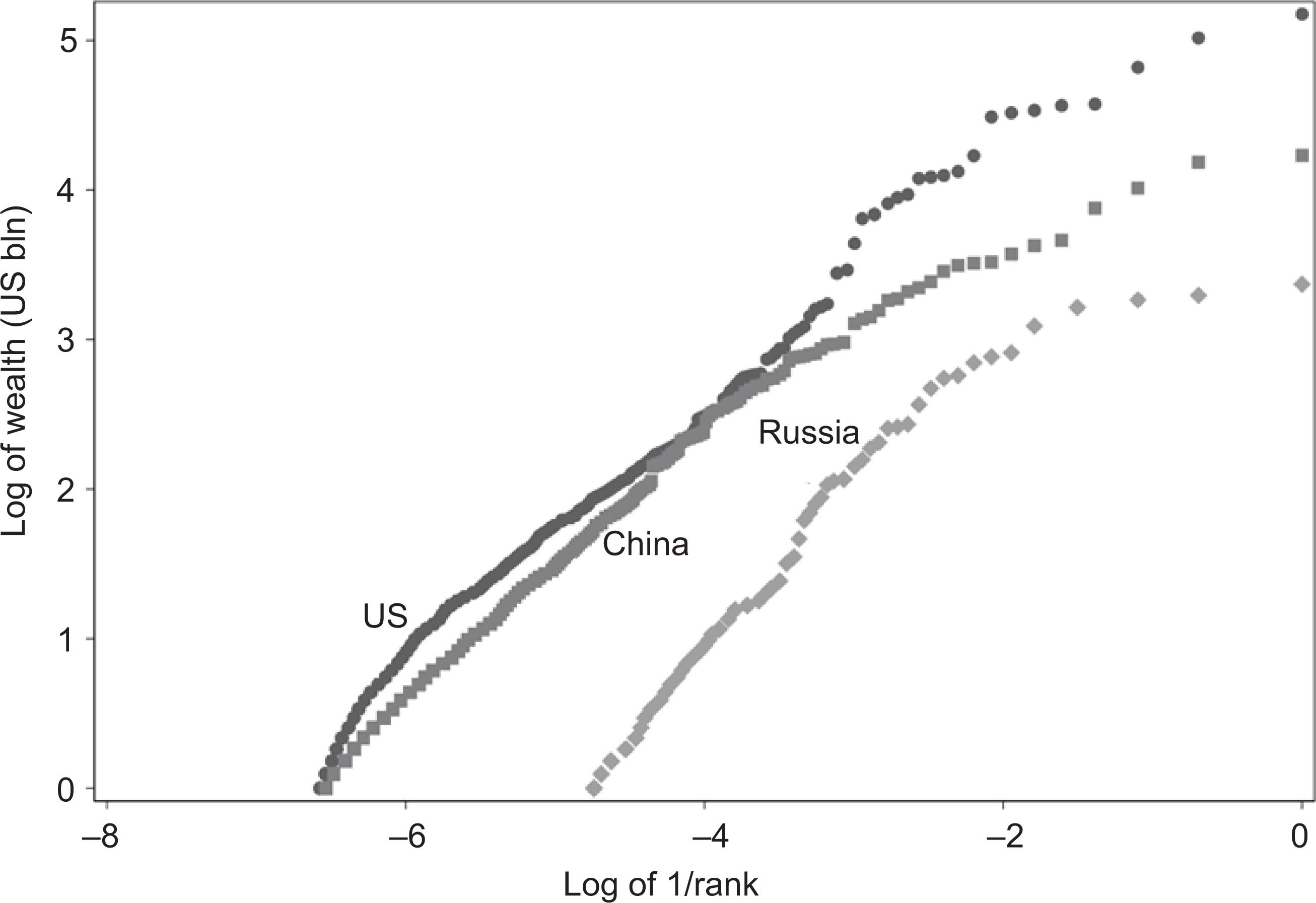
As Pareto discovered, the relationship of the natural log of wealth at the top and that of the log of the rank (taking the inverse of rank so that the wealthiest are at the right) is almost a straight line. The coefficients differ slightly across countries and the intercepts differ according to the wealth of the particular set of billionaires. Selecting the members of the Forbes’ global list for 2021 who are listed as citizens of the five countries, whose citizens comprise at least 4% of the total—the United States, China (including Hong Kong), India, Germany, and Russia—we compare the slopes of the distributions of their wealthiest citizens. The plots are shown in Figure 3.
All five signatures are nearly straight-line curves. The linear regression coefficients (α) for all range from 0.83 to 0.967. However, some deviations are observed from the straight line. If we focus on the United States, Russia, and China, we observe that the curves bend slightly downward in the case of Russia and China, but not in the United States. This suggests that the inequalities at the very top are less pronounced in Russia and China than in the United States (Figure 4).
It bears remembering that the log scale truncates differences between actual levels of wealth. A one-point higher value on the log scale means a person is 2.7 times wealthier than a person with a logged wealth value one point lower. As observed by Pareto, the distribution of top-end wealth has a very similar structure across the world.
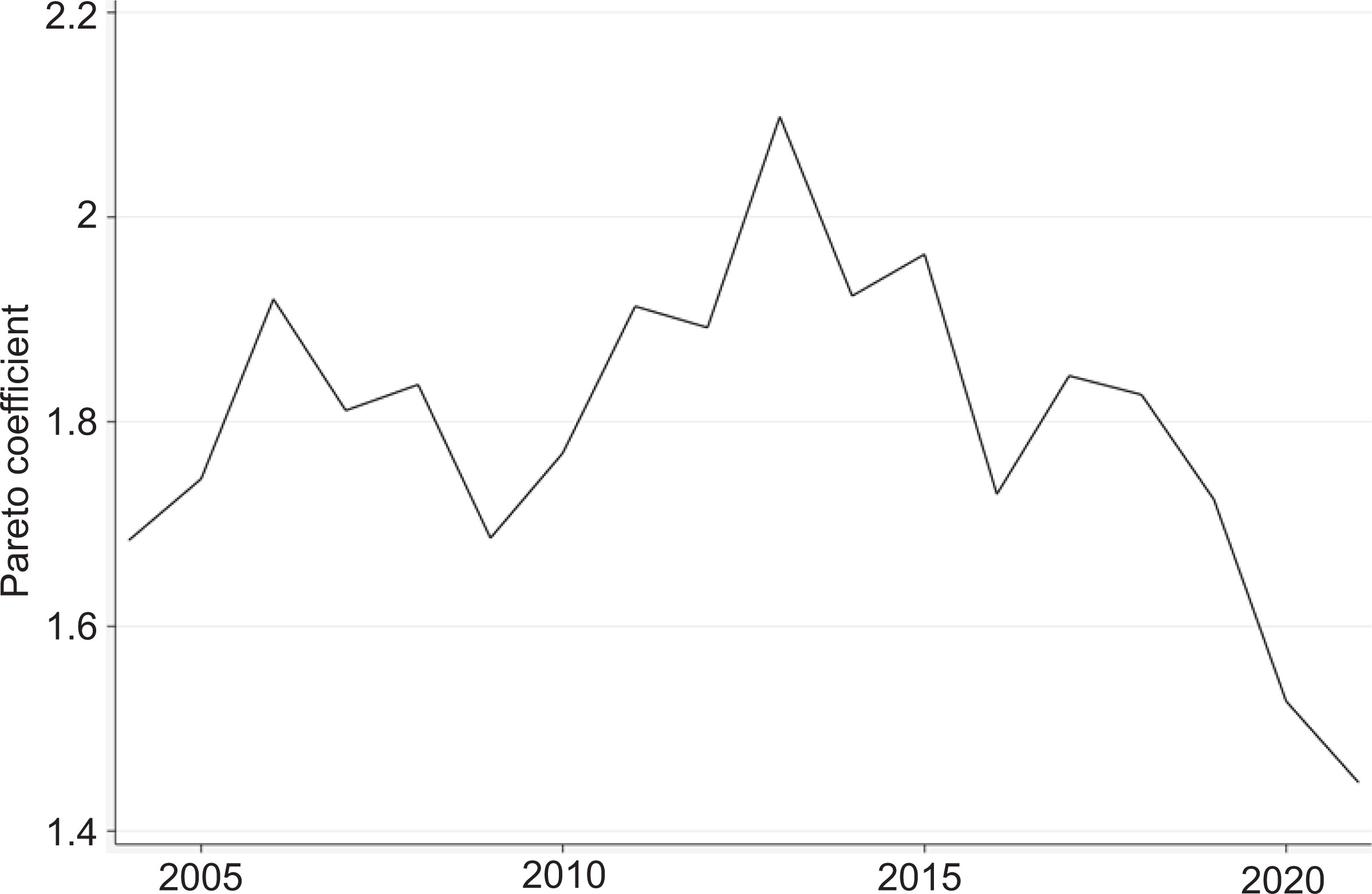
On the other hand, even for the Forbes’ global top 100 individuals, there is some tendency toward greater concentration of wealth since 2013, and especially after the COVID pandemic drove asset prices for digital commerce companies upward. Figure 3 shows changes in the Pareto (α) coefficients over time for those on the Forbes’ global 100. The fact that α has fallen below 1.5 for the global wealthiest over the last decade shows that the concentration of wealth at the top has become significantly greater. Figure 5 displays the trend.
The data indicate that for the top 100 individuals, the last decade has witnessed a significant increase in concentration of wealth. These trends support the supposition that the processes generating accumulation of wealth nationally foster higher rates of wealth accumulation for the wealthiest. At the same time, we have seen significant variation across countries in the degree to which the growth of wealth in the country is accompanied by increase in top-end wealth shares. Without attempting a complete explanation of this variation, we can point to the policies and institutions that foster faster top-end wealth accumulation.
Political versus Market Factors in Wealth Accumulation
Trends in the accumulation of top-end wealth shed light on the forces shaping economic growth and distribution more generally in the economy. Some economists who analyze wealth inequality assume that market forces are decisive in shaping wealth formation. For example, some have proposed models based on heroic assumptions about “returns to talent” or “matching” between talent and super-star firms (Gabaix, 2009; Gabaix & Landier, 2008; Jones, 2015; Jones & Kim, 2018). Others argue that differential levels of “human capital” underlie inequality, reconciling the data on actual inequality with the human capital theory by including qualities such as reputation, “rent-extraction ability,” and social networks under the broad rubric of human capital (Smith, Yagan, Zidar, & Zwick, 2019). Under such a loose definition, however, any political influence, corruption, or cronyism by elites that goes unpunished could be classified as human capital. Alternatively, often the share of self-made billionaires as opposed to those who inherited their wealth is used as a proxy for the degree to which entrepreneurship accounts for wealth formation (cf. Lane, 2021; Treisman, 2016).7 The fallacy here is that in some cases, manipulation of tax and regulatory rules, political favoritism, or corruption could also underlie the rise of self-made billionaires.
Others find it implausible that market competition can fully explain the Pareto nature of the distribution of returns to wealth. For example, because the wealthiest are better positioned than others to hide and to underreport their wealth (since more of their income lacks third-party documentation), non-market forces can account for wealth accumulation (Johns & Slemrod, 2010). Moreover, in the United States, in recent decades, the rate of audits of the richest taxpayers has declined, while that of the poor has risen (Bloomquist, 2019). The wealthy have also been able to influence federal and state-level rules on disclosure of assets. For example, a number of billionaires from around the world, some with histories of money-laundering and influence-peddling, have created legal instruments in the US state of Wyoming that are shielded from oversight (Cenziper & Fitzgibbon, 2021). Gabriel Zucman estimates that some 8% of the world’s wealth is sheltered in such offshore accounts. In the case of Russia, the amount of wealth hidden in such tax havens equals approximately half of total personal wealth (Zucman, 2019).
A number of studies have demonstrated that one reason for the exponential nature of the growth of wealth at the top is that investment assets for the wealthiest experience higher returns than those for the less-wealthy, even adjusted for risk. For this reason, it is incorrect to assume the same risk-adjusted rate of return on capital for all classes of investors (Acemoglu & Robinson, 2015). Abundant empirical study confirms that the wealthy do receive higher average returns on capital, even adjusted for risk (Saez & Zucman, 2020). As Schulz and Milakovic point out, whether the wealthier are wealthier because they obtain higher returns on their wealth, or whether they receive higher returns because they are wealthier, are observationally equivalent (Schulz & Milakovic, 2021). However, the data are consistent with a finding that the rates at which wealth increases rise with levels of wealth, much as income growth tends to increase in proportion to the level of income (Schulz & Milakovic, 2021). The evidence supports a conclusion that the rules governing the operation of capital markets favor those with the greatest wealth. Not only do the wealthy individuals press for the conversion of public to private wealth, they also manipulate capital markets so as to shift market risk to the public. Formal and informal rules against allowing financial institutions that are too “systemically important” to fail amount to implicit subsidies that allow them to realize higher profits from lending operations than those facing full market risk (International Monetary Fund [IMF], 2014). Similar relationships between financial structures and government have been identified in markets for housing, urban infrastructure, and student loans, all of which are poorly monitored regulated monopolies (Frame et al., 2015; Frank, 2015; McDonald, 2012; Michel, 2020; Reiss, 2009). In each case, policymakers’ efforts to serve public interests by creating incentives for private investment allowed financial institutions to realize higher returns by evading oversight and shifting losses to the public treasury. The alliance of the financial industry with sympathetic government policymakers resulted in the weakening of both market competition and government regulation. As a general rule, we can postulate that the more concentrated is ownership of wealth, the more wealth holders can concentrate their influence over policymaking in order to create the most favorable institutional environment for rent seeking (Achen & Bartels, 2016; Bartels, 2008; Hacker & Pierson, 2010, 2020; Hertel-Fernandex, 2019; McCarty, Poole, & Rosenthal, 2016; Page & Gilens, 2018; Schlozman et al., 2018).
The rising concentration of wealth in a society not only enables the wealthy to exert greater power over policymakers but it also increases the share of capital income in their total income and, with it, the total share of capital income in a society relative to labor income (Piketty, 2014). Thomas Piketty argues that this is a general tendency unless it is disrupted by exogenous events, such as wars, revolutions, or major political reform (Piketty, 2022). Whether the share of capital income is rising can only be determined on the basis of assumptions about how sources of income are classified, since many types of income can be treated as either capital or labor income, depending on how it is defined (Piketty, Saez, & Zucman, 2018, 2021; Saez, 2019; Smith, Zidar, & Zwick, 2021) For example, owners of closely held businesses treat business income as personal income, paying the (usually lower) personal income tax rate on it. How much of their income should be treated in national income accounts as labor income and how much as a return on capital requires assumptions. For example, in the case of the owners of large automobile distributorships, who comprise a high share of the top 1% of incomes in the United States, how much of their income reflects their skills as managers and salespeople, and how much is a return on the capital stock of their inventory?
How would we adjudicate between market-based and political explanations for the observed patterns of wealth accumulation? One way is to examine the relationship between the market power of firms and the growth of profits, incomes, and wealth. Market power measures a firm’s ability to influence prices. Low competition-monopoly in the extreme case—and government-granted privileges confer market power on a firm. Market power enables a firm to generate profits beyond the level that would occur in the presence of full competition. When those profits are returned as income to the owners of the capital or to senior executives, income inequality rises unless and until competitive forces dissipate the profits. Income inequality as results in higher wealth inequality described above.
Market power has become a significant part of corporate value in the United States. For example, the level of Tobin’s Q—which measures the ratio between companies’ market value and their net worth in replacement terms—has risen. Many economists regard Tobin’s Q as a valid measure of market power (Salinger, 1984).8 The theory behind the measure is that in a fully competitive market, shareholders are compensated for risk by the expectation of a sufficient future stream of profits. In a competitive marketplace, if Tobin’s Q for a firm stays above 1 for a long time, competitors should be able to enter the market and capture a share of the available profits. However, Tobin’s Q for nonfinancial American corporations overall has been well above 1 for most of the period since the early 1980s; it has tracked corporate profits, rather than productivity. The increase in profitability has not been driven by an increase in productivity (Grullon, Larkin, & Michaely, 2017). Instead, it has produced an enormous increase in rent-extraction by owners and managers of firms (Comanor & Smiley, 1975; De Loecker & Eeckhout, 2017; Furman & Orszag, 2015; Gans et al., 2017; Grullon et al., 2017; Khan & Vaheesan, 2017).
In any economy, the decoupling of profitability from productivity is a strong indication that corporations are extracting rents through market power. In an economy where firms exercise market power, profits are likely to reflect no greater efficiency or innovation but rather the ability to prevent competitors from eating away profit margins. In a fully competitive market, producers cannot charge markups above marginal cost. Open entry into and out of the marketplace means that profits are realized through gains in efficiency or innovation. For that reason, economists tend to operate on the assumption that profits measure productivity at the firm level, just as they believe wages are set at the rate of the value of a marginal unit of labor to revenue. These assumptions, however, fall apart in an economy where the wealthy influence the rules of the market.
Market power allows firms to extract rents in several ways, apart from raising prices above the competitive level. They may be able to reduce costs by shifting risk to taxpayers or reducing borrowing costs (e.g., by winning government guarantees of a bailout in case of a liquidity crisis). If they have market power vis-à-vis labor, they can set wages below marginal product. As Louis Brandeis observed as early as in 1913, higher efficiency normally yields higher net earnings. However, we cannot assume that higher earnings are a reflection of higher efficiency: they may result from market power (Brandeis, 1913). Therefore, when we observe that firm profits grow while productivity falls, we can infer that firms possess market power and are using it to extract rents. This has been the case in the United States following the liberalization of the late 1970s and early 1980s. It is still more pronounced in countries such as Russia and China.
For example, Figures 6 and 7 indicate that the profit rate for business—in this case, nonfinancial business corporations- has risen significantly since the late 1970s, while the growth rate of total factor productivity has declined slowly.
Source: TFP: San Francisco Federal Reserve: Utilization-adjusted quarterly-TFP series for the U.S. Business Sector and WID World. Adults, equal split. John G. Fernald, A quarterly, Utilization-Adjusted Series on Total Factor Productivity. FRBSF Working Paper 2012–2019 (updated March 2014). https:www.frbsf.org/economic-research/indicators-data/total-factor-productivity-tfp/ and Profits: FRED St. Louis: After-tax profit per unit of real gross value added of nonfinancial corporate business (A466RD3Q052SBEA). https://fred.stlouisfed.org/series/A466RD3Q052SBEA.
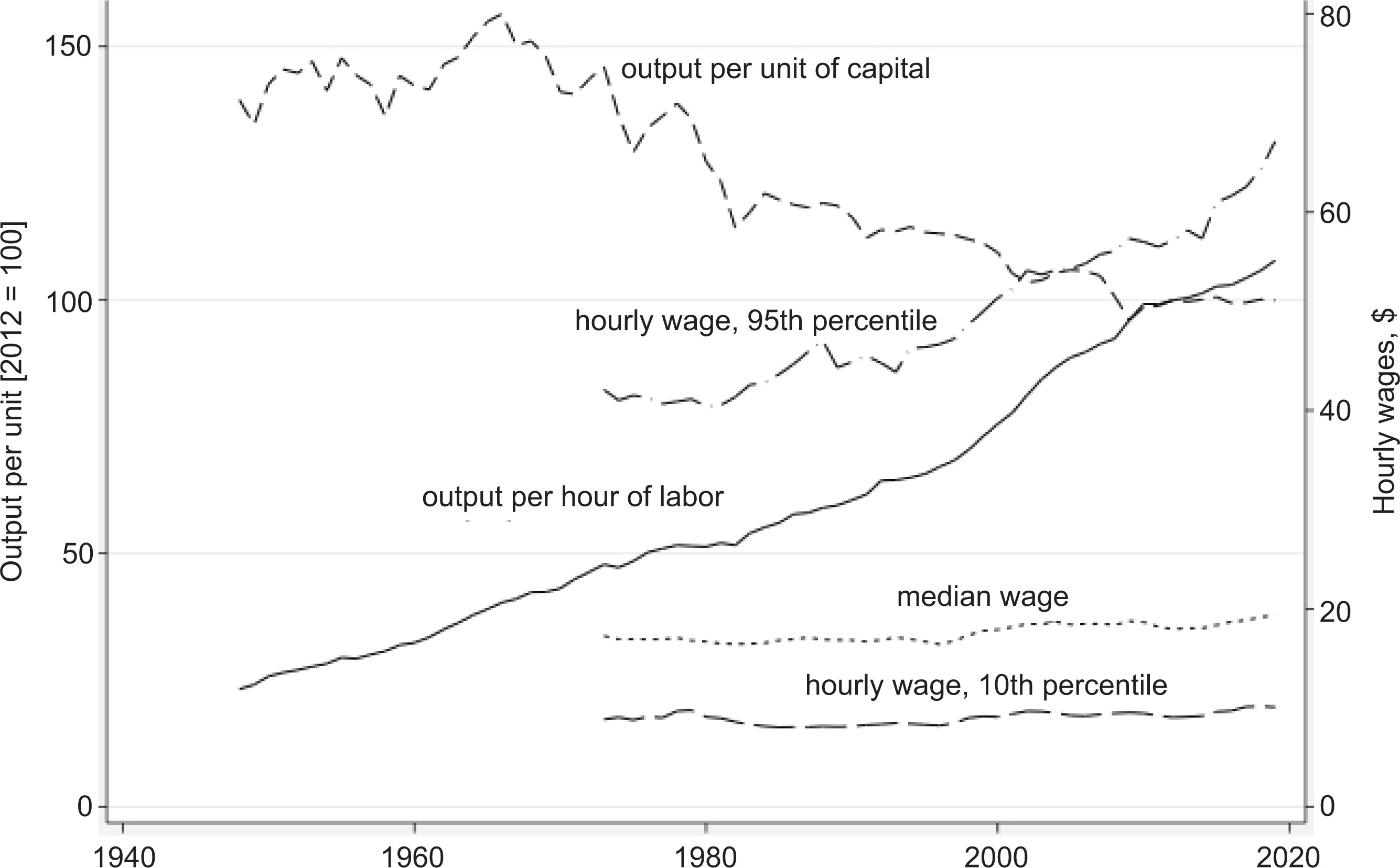
Source: BLS multifactor productivity series (https//www.bls.gov/mfp); EPI wage data library (https//www.epi.org/data/#?subject=wage.percentiles)
Total factor productivity refers to the part of output growth that is not explained by adding more units of capital and labor; it is often interpreted as ability to make better use of existing technology. When we break out capital and labor productivity separately, we find that output per unit of capital has declined whereas that of labor has risen. However, all the gains have gone to the very top percentiles of the income distribution, as indicated in Figure 7.
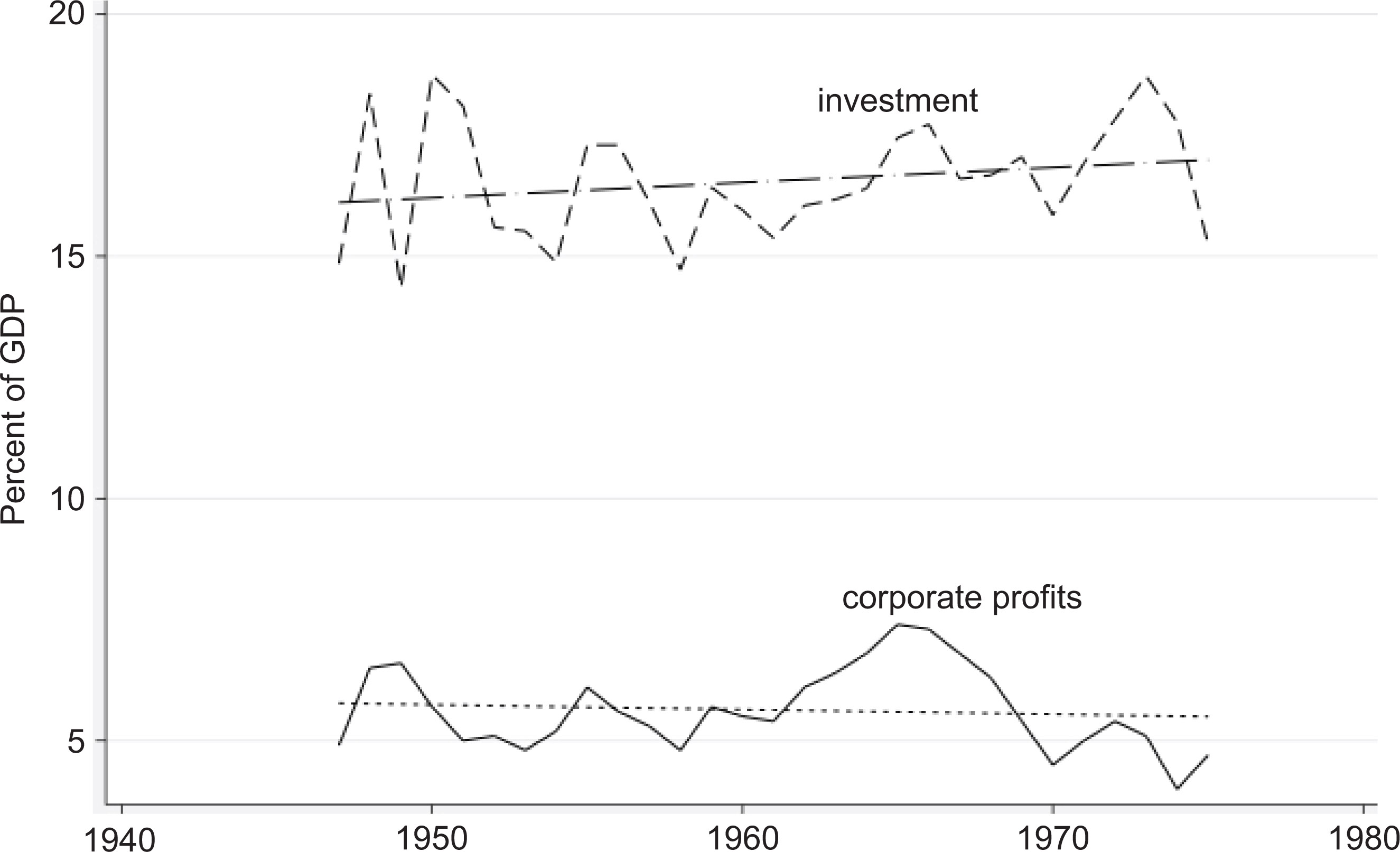
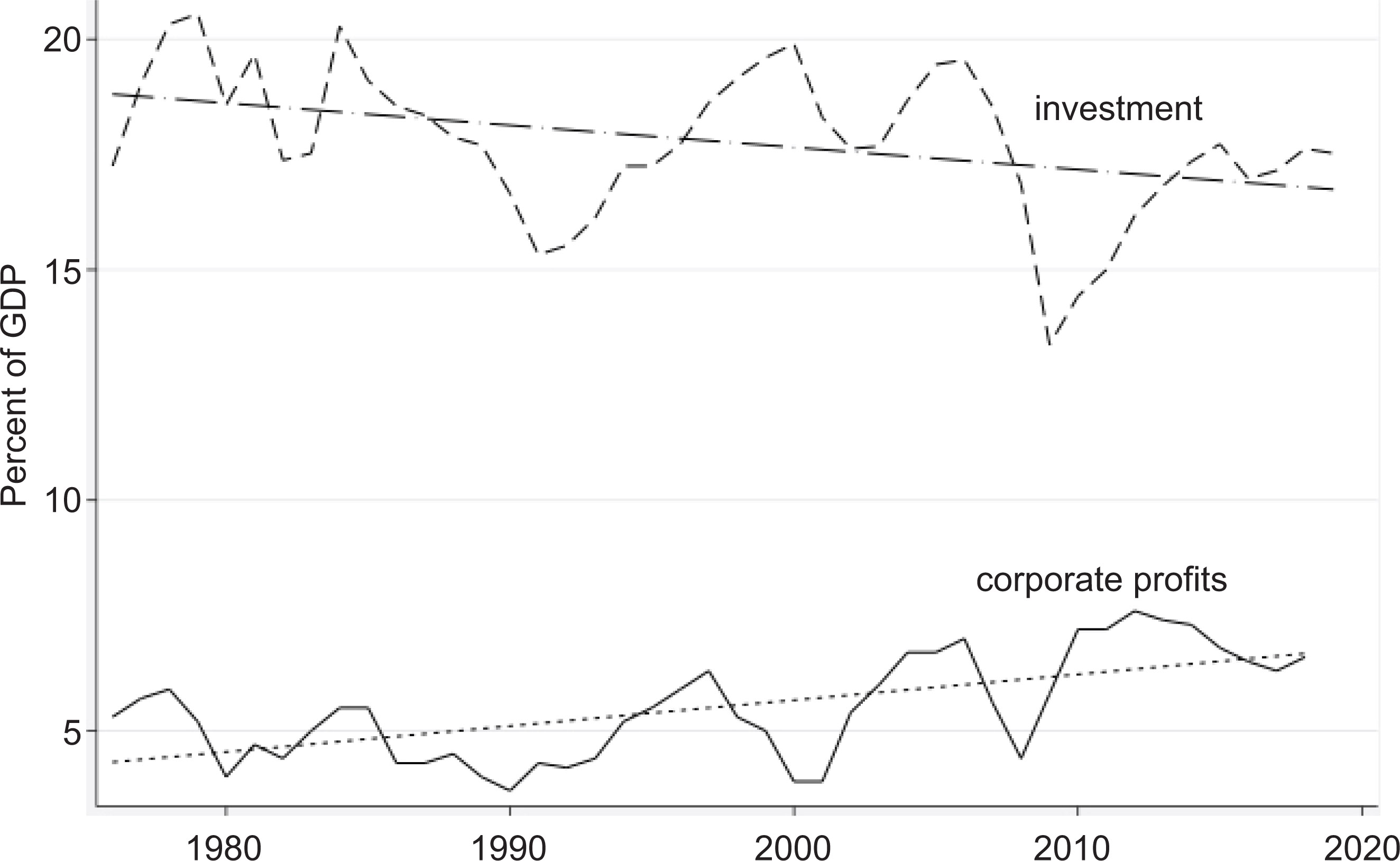
Similarly, after the late 1970s, the relationship between investment and profits as shares of gross domestic product (GDP) has shifted. Before the late 1970s, profit as a share of GDP was slowly declining whereas that of investment was rising. After the late 1970s, the trends were reversed. Profits as a share of GDP began rising whereas that of investment declined (Figures 8 and 9).
Source: FRED St. Louis, After-tax corporate profits, domestic industries as share of GDP; Gross private domestic investment as share of GDP (https://fred.stlouisfed.org).
Source: FRED St. Louis, After-tax corporate profits, domestic industries as share of GDP; Gross private domestic investment as share of GDP (https://fred.stlouisfed.org).
Economists debate about the scale of market power exercised by firms in the United States (Basu, 2019; De Loecker, Eeckhout, & Mongey, 2021; Traina, 2018). This is not the place to settle the question. Two points will suffice here. First, where and for whatever reason it exists, greater market power enables firms to realize higher profits than would be possible under conditions of perfect competition. Among the conditions that enable firms to exercise market power are restrictions on competition. These may result from a first-mover innovation, but they also often reflect favorable treatment by government-tax breaks, favorable regulation, exclusive access to particular markets, and the like. Under such conditions, profitability is a poor gauge of productivity; indeed, the degree of the wedge between productivity and profitability can be taken as a measure of the level of advantage that allows firms to realize higher profits without increasing efficiency or productivity. Second, the distribution of those profits affects not only the aggregate returns to capital and labor but also shapes how those returns are distributed among the owners of capital, the executives of the firms, and the rest of the firm’s employees. Under current accounting rules in the United States, a firm may treat the salaries of all managers as part of its “selling and general administrative” costs, that is, overhead costs; which are treated as deductible expenses under tax law and as reducing net profits. Firms report two types of operating expenses, “cost of goods sold” (COGS) and “selling and general administration” (SGA) costs. COGS are considered variable costs whereas SGA (overhead) is treated as fixed costs. Generally, wages of employees are recorded as part of COGS along with most intermediate goods whereas the salaries of executives, along with marketing expenses, are treated as fixed costs (i.e., they do not vary with the level of output in the short run). If compensation to executives rises relative to compensation to workers, regardless of the output elasticity of their contributions to value-added, and if market power enables firms to increase both profits and compensation to executives and owners, then the salary of the highest-paid managers and the returns to the owners will rise more quickly than that of lower-paid workers. In effect, compensation can rise for executives at the expense of increase in salaries of workers, a pattern consistent with the data. The cumulative effect of these labor market income differentials would in turn enable the accumulation of top-end wealth through the recursive process discussed above. The accumulation of individual-level wealth that we have observed is consistent with this conjecture.
As we know, a large portion of top-end income gains is capitalized as wealth, and the higher the income, the higher the share of the income that is converted to wealth. Moreover, the greater the level of wealth, the higher the rate of return available to it. The cumulative nature of wealth in turn becomes a major driver of income inequality, both within and across generations. Although asset values may rise and fall, wealth accumulates because of the higher incomes and investment rates of the wealthy. Since upward swings in the profit share of GDP drive concentration of top-end income upward, as incomes and wealth rise at the top, wealth accumulation enables the return on wealth to drive top-end incomes and wealth inequality still further.
| OLS with robust standard errors | ||||||
|---|---|---|---|---|---|---|
| DV: Top 1% wealth share | Coefficient | Std. error | t | P > t | 95% Confidence interval | |
| Profit share of GDP | 0.0202 | 0.0036 | 5.66 | 0.0000 | 0.0131 | 0.0273 |
| GDP growth | –0.0044 | 0.0014 | –3.06 | 0.003 | –0.0072 | –0.0015 |
| Constant | 0.1893 | 0.0212 | 8.91 | 0.0000 | 0.1469 | 0.2316 |
| R 2 0.361 | ||||||
| F(2, 71) = 19.89 | ||||||
| Prob > F = 0.0000 | ||||||
| No. obs. = 74 | ||||||
| Root MSE = 0.03027 | ||||||
Conclusions
The evidence presented here indicates that wealth flows to wealth at a rate proportional to the relative size of wealth. Although radical changes in market conditions, taxation, and vigorous enforcement of anti-monopoly law can all affect the accumulation of both aggregate and individual-level wealth, the evidence from the Forbes lists as well as the WID and the Credit Suisse data indicates that accumulation outweighs dissipation in the process of wealth accumulation. To be sure, an act of government—as when the government seizes an oligarch’s assets—can affect wealth accumulation at the individual level. However, if the wealth so seized is simply transferred (e.g., the assets of an oil company are seized by the state and turned over to another oligarch), aggregate wealth accumulation continues. Therefore, although wealth certainly can be used to exercise political influence, the relative balance of advantage between regime and oligarchs can be tilted in favor of one side or another.
As noted above, much wealth does not generate income, at least until the assets are sold. Much wealth takes the form of lifestyle assets, such as villas and super yachts, or is parked in offshore accounts. There it is sheltered from taxation and is not necessarily used productively. By exerting political influence, the wealthy are able to hide and underreport their wealth and shape federal and state-level rules on disclosure of assets. As a result, perhaps 8% of global wealth is sheltered in off-shore accounts.
In the United States, the market power of firms likely explains much of the story of wealth accumulation. Although the level of aggregate market power is debated, it is undeniable that some firms and some sectors exercise a higher level of market power than others. Some portion of a firm’s profits is returned to the owners and as compensation to executives under the category of SGA; it is not treated as a return to labor. The aggregate profit rate in the United States has risen whereas both investment and capital productivity have declined. There is clear evidence, therefore, that the gap between productivity and profitability has widened in the aggregate along with the share of wealth owned by the wealthiest. At the same time, individual-level wealth has shown a strong tendency to accumulate at a rate proportional to the level of wealth, consistent with the pattern of exponential growth first observed by Pareto.
Notes
- The number of families is much smaller than the number of households. There are approximately 84 million families and 128 million households. Whether we treat the top 400 as representing the wealth of families or households, this segment is obviously an extremely small percentage of the population. ⮭ ⮭
- Data from online appendix in Saez & Zucman (2016). ⮭
- As Stiglitz (2015) has pointed out, not all wealth is capital, although capital is a form of wealth. Some wealth takes the form of other assets, such as artwork, villas, and super yachts, that only yield income when they are sold. Importantly for the purpose of this paper, when income is capitalized—as when profits or earnings are converted to investment capital—it becomes wealth. Higher rates of savings and investment among higher-income individuals, therefore, have a cumulative effect in widening the wealth gap between the wealthiest and others. This latter phenomenon led Thomas Piketty to formulate his model of the recursive nature of income and wealth over time. ⮭
- These report somewhat different series. Both employ the Pareto distribution to estimate top-end wealth shares from published national accounts data, household surveys, and Forbes lists. The Credit Suisse Global Wealth data, however, include both financial and nonfinancial assets, less debt, whereas the WID bases its estimates on financial wealth. WID’s global estimates cover a long period for most countries and estimates both for top and bottom shares whereas the Credit Suisse Global Wealth data only provide top shares data since 2010 and mean wealth since 2000. Therefore, to provide longer series to examine change in top and bottom shares, I use the WID World Series. ⮭
- The top 200 and the top 100 also experienced a CAGR of about 9.5%. ⮭
- This is the basis of Thomas Piketty’s theory:
That is, the share of income from capital equals the rate of return on capital times the ratio of capital to income. Moreover, over time, β = s/g, where s represents net savings and g is the rate of growth of national income. Then, if r > g, the share of capital income in national income rises, and, as a result, the concentration of ownership of capital. Although skeptics have pointed out that r cannot exceed g for extended periods of time—due to amortization of capital, rates of elasticity of substitution of capital for labor lower than unity, the fact that much wealth takes the form of non-capital assets, such as real estate, that are subject to asset bubbles, and so on—Piketty supplies considerable evidence that r can in fact exceed g over long periods of time. One example is the very high long-term returns on large private university endowments, which are much higher than GDP or income growth (Piketty 2014). ⮭The ratio of capital to income in a society is designated β
The share of income from capital is α.
The rate of return from capital is r.
Piketty postulates that α = r × β.
- See, for example, Lane (2021). Treisman (2016) examines the Forbes list of Russian billionaires to determine how many made their fortunes in the early wave of privatization. ⮭
- Salinger claimed that Tobin’s Q was not high. However, his data ended in 1970s and did not observe the sustained high values of the Tobin’s Q measure for the stock market in recent decades. ⮭
The author is grateful to Ara Omotowa for research assistance. This paper is part of a collaborative research with Andrei Yakovlev and Alexei Chikin under the auspices of the International Center for the Study of Institutions and Development at the Higher School of Economics, Moscow, Russian Federation. The project was funded by the Higher School under the auspices of the Basic Research Program of the National Research University Higher School of Economics. The author is grateful to Andrei Yakovlev, John Reuter, Michael Alexeev, and Amanda Zadorian for comments on the earlier version of this paper
References
Acemoglu, D., & Robinson, J.A. (2015). The rise and decline of general laws of capitalism. Journal of Economic Perspectives, 29(1), 3–28.
Achen, C.H., & Bartels, L.M. (2016). Democracy for realists: Why elections do not produce responsive government. Princeton, NJ: Princeton University Press.
Armour, P., Burkhauser, R.V., & Larrimore, J. (2016). Using the Pareto distribution to improve estimates of top-coded earnings. Economic Inquiry, 54(2), 1263–12727.3.
Atkinson, A.B. (2017). Pareto and the upper tail of the income distribution in the UK: 1799 to the present. Economica, 84, 129–156.
Atkinson, A.B., Piketty, T., & Saez, E. (2011). Top incomes in the long run of history. Journal of Economic Literature, 49(1), 3–71.
Bartels, L.M. (2008). Unequal democracy: The political economy of the new gilded age. Princeton, NJ: Princeton University Press.
Basu, S. (2019). Are price-cost markups rising in the United States? A discussion of the evidence. Journal of Economic Perspectives, 33(3), 3–22.
Bloomquist, K.M. (2019). Regional bias in IRS audit selection. Tax Notes, 162(9), 987.
Brandeis, L.D. (1913). Competition. American Legal News 24(1), 1–14.
Brzezinski, M. (2014). Do wealth distributions follow power laws? Evidence from “Rich Lists.” Physica A, 406, 155–162.
Cenziper, D., & Fitzgibbon, W. (2021). The “cowboy cocktail”: How Wyoming became one of the world’s top tax haven. Washington Post, December 20.
Collins, C. (2021, June 16). Silver spoon oligarchs: How America’s 50 largest inherited-wealth dynasties accelerate inequality. Report. Washington, DC: Institute for Policy Studies. Retrieved from https://ips-dc.org/report-americas-wealth-dynasties-2021/https://ips-dc.org/report-americas-wealth-dynasties-2021/
Comanor, W.S., & Smiley, R.H. (1975, May). Monopoly and the distribution of wealth. The Quarterly Journal of Economics, 89(2), 177–194. http://dx.doi.org/10.2307/1884423.http://dx.doi.org/10.2307/1884423
De Loecker, J., & Eeckhout, J. (2017, August). The rise of market power and the macroeconomic implications. NBER Working Paper Series, No. 23687. Cambridge, MA: National Bureau of Economic Research (NBER). http://dx.doi.org/10.3386/w23687http://dx.doi.org/10.3386/w23687
De Loecker, J., Eeckhout, J., & Mongey, S. (2021, May). Quantifying market power and business dynamism in the macroeconomy. NBER Working Paper 28761. Cambridge, MA: National Bureau of Economic Research (NBER).
Frame, W.S., Fuster, A., Tracy, J., & Vickery, J. (2105). The rescue of Fannie Mae and Freddie Mac. Journal of Economic Perspectives, 29(2), 25–52.
Frank, B. (2015). Frank: A life in politics from the great society to same-sex marriage. New York, NY: Farrar, Straus and Giroux.
Freund, C., & Oliver, S. (2016, February). The origins of the superrich: The billionaire characteristics database. Working Paper 16-1. Washington, DC: Peterson Institute for International Economics.
Furman, F., & Orszag, P. (2015, October 16). A firm-level perspective on the role of rents in the rise in inequality. Retrieved from http://goodtimesweb.org/industrial-policy/2015/20151016_firm_level_perspective_on_role_of_rents_in_inequality.pdf.http://goodtimesweb.org/industrial-policy/2015/20151016_firm_level_perspective_on_role_of_rents_in_inequality.pdf
Gabaix, X. (1999). Zipf’s law for cities: An explanation. The Quarterly Journal of Economics, 114(3), 739–767.
Gabaix, X. (2009). Power laws in economics and finance. Annual Review of Economics, 1(1), 255–293.
Gabaix, X., & Landier, A. (2008). Why has CEO pay increased so much? The Quarterly Journal of Economics, 123(1), 49–99.
Gans, J., Leigh, A., Schmalz, M., & Triggs, A. (2019). Inequality and market concentration, when shareholding is more skewed than consumption. Oxford Review of Economic Policy, 35(3), 550–563.
Grullon, G., Larkin, Y., & Michaely, R. (2017, Aug). Are U.S. industries becoming more concentrated? Retrieved from https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2612047.https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2612047
Hacker, J.S., & Pierson, P. (2010). Winner-take-all politics. New York, NY: Simon & Schuster.
Hacker, J.S., & Pierson, P. (2020). Let them eat tweets: How the right rules in an age of extreme inequality. New York, NY: Liveright.
Hertel-Fernandez, A. (2019). State capture: How conservative activists, big businesses, and wealthy donors reshaped the American states—and the nation. New York, NY: Oxford University Press.
International Monetary Fund (IMF). (2014, Apr). Global financial stability report: Moving from liquidity- to growth-driven markets. Retrieved from http://www.imf.org/en/Publications/GFSR/Issues/2016/12/31/Moving-from-Liquidity-to-Growth-Driven-Marketshttp://www.imf.org/en/Publications/GFSR/Issues/2016/12/31/Moving-from-Liquidity-to-Growth-Driven-Markets
Johns, A, & Slemrod, J. (2010, Sep). The distribution of income tax noncompliance. National Tax Journal, 63(3), 397–418.
Jones, C.I. (2015). Pareto and Piketty: The macroeconomics of top income and wealth inequality. Journal of Economic Perspectives, 29(1), 29–46.
Jones, C.I., & Kim, J. (2018). A Schumpeterian model of top income inequality. Journal of Political Economy, 126(5), 1785–1826.
Khan, L.M., & Vaheesan, S. (2017). Market power and inequality: The antitrust counterrevolution and its discontents. Harvard Law and Policy Review, 11, 235–294.
Krugman, P. (1996). Confronting the mystery of urban hierarchy. Journal of the Japanese and International Economies, 10, 399–418.
Lane, R. (2021). Operation wealth speed. Forbes, April 6.
Mankiw, N. Gregory. (2013). Defending the one percent. Journal of Economic Perspectives, 27(3), 21–34.
McCarty, N., Poole, K.T., & Rosenthal, H. (2016). Polarized America: The dance of ideology and unequal riches (2nd ed.). Cambridge, MA: MIT Press.
McDonald, O. (2012). Fannie Mae and Freddie Mac: Turning the American dream into a nightmare. London: Bloomsbury Academic.
Michel, N. (2020). Fannie Mae and Freddie Mac need strict bank-like capital requirements. Forbes, March 9.
Newman, M.E. J. (2005). Power law, Pareto distributions and Zipf’s law. Contemporary Physics, 46(5), 323–351.
Page, B.I., & Gilens, M. (2018). Democracy in America? What has gone wrong and what we can do about it. Chicago, IL: University of Chicago Press.
Piketty, T. (2014). Capital in the twenty-first century (Arthur Goldhammer, Trans.). Cambridge, MA: Harvard University Press.
Piketty, T. (2022). A brief history of equality. Cambridge, MA: Harvard University Press.
Piketty, T., Saez, E., & Zucman, G. (2018). Distributional national accounts: Methods and estimates for the United States. The Quarterly Journal of Economics 133(2), 553–609.
Piketty, T, Saez, E., & Zucman, G. (2021, Oct). Top wealth in America: New estimates and implications for taxing the rich. NBER Working Paper 29374. Cambridge, MA: National Bureau of Economic Research (NBER).
Price, C.C., & Edwards, K.A. (2020, Sep). Trends in income from 1975 to 2018. RAND Education and Labor Working Paper WR-A516-1. https://www.rand.org/pubs/working_papers/WRA516-1.html. Santa Monica: RAND Corporation.https://www.rand.org/pubs/working_papers/WRA516-1.html
Reiss, D., (2009). The role of the Fannie Mae/Freddie Mac Duopoly in the american housing market. Journal of Financial Regulation and Compliance, 17(3), 336–348.
Saez, E. (2019, Mar 2). Striking it richer: The evolution of top incomes in the United States (updated with 2017 final estimates).
Saez, E., & Zucman, G. (2016). Wealth inequality in the United States since 1913: Evidence from capitalized income tax data. Quarterly Journal of Economics, 131(2), 519–578.
Saez, E., & Zucman, G. (2018). Distributional national accounts: Methods and estimates for the United States. The Quarterly Journal of Economics, 133(2), 553–609.
Saez, E., & Zucman, G. (2019). The triumph of injustice: How the rich dodge taxes and how to make them pay. New York, NY: Norton.
Saez, E., & Zucman, G. (2020, Oct). Trends in US income and wealth inequality: Revising after the revisionists. NBER Working Paper 27921. Cambridge, MA: National Bureau of Economic Research (NBER).
Salinger, M.A. (1984, Summer). Tobin’s q, unionization, and the concentration-profits relationship. RAND Journal of Economics, 15(2), 159–170.
Schlozman, K.L, Verba, S., & Brady, H.E. (2018). Unequal and unrepresented: Political inequality and the people’s voice in the new gilded age. Princeton, NJ: Princeton University Press.
Schulz, J., & Milakovic, M. (2021). How wealthy are the rich? The Review of Income and Wealth. http://dx.doi.org/10.1111/roiw.12550.http://dx.doi.org/10.1111/roiw.12550
Smith, M., Yagan, D., Zidar, O.M., & Zwick, E. (2019, May). Capitalists in the twenty-first century. NBER Working Paper 25442. Cambridge, MA: National Bureau of Economic Research (NBER).
Stiglitz, J.E. (2015). The origins of inequality, and policies to contain it. National Tax Journal 68(2), 425–448.
Strogatz, S. (2009). Guest Column: Math and the City. New York Times, May 19.
Traina, J. (2018, Feb 8). Is aggregate market power increasing? Production trends using financial statements. Retrieved from https://ssrn.com/abstract=3120849. Rochester, NY: SSRN. http://dx.doi.org/10.2139/ssrn.3120849.https://ssrn.com/abstract=3120849http://dx.doi.org/10.2139/ssrn.3120849
Treisman, D. (2016). Russia’s billionaires. American Economic Review: Papers & Proceedings, 106(5), 236–241.
Zucman, G. (2019). Global wealth inequality. Annual Review of Economics. 11, 109–138.
Thomas F. Remington is a Visiting Professor of Government, Harvard University, and Goodrich C. White Professor of Political Science (Emeritus), Emory University. He can be contacted at tremington@fas.harvard.edu.