Introduction
Since the 1960’s, attaining the most accurate form for modeling the mechanics of the human brain has been studied and the merits of various models have been debated. However, due to the unique characteristics of the human brain and limited ability to conduct tests on it, a consensus has yet to be made in determining its material properties. Because of this, there is much variation in the material parameters used by researchers. Table 1 shows the variation in brain material parameters for Ogden’s model of hyperelasticity that have been used in a few well-known publications. The variation in material parameters shown in Table 1 suggests that, under the Ogden model, one set of parameters that models the hyperelasticity of the brain with complete accuracy may not be attainable.
Shown below are the values used for the unrelaxed shear modulus, μ0, and alpha constant, α, for first order Ogden models of hyperelasticity from four publications. The comma separated values represent parameters for gray and white matter of the brain, respectively.
| α | μ0 [Pa] | Publication |
|---|---|---|
| −4.70 | 842 | Miller and Chinzei, 2002 [1] |
| 6.95 | 5160 | Rashid et. al., 2012 [3] |
| 0.038, 0.063 | 182, 263 | Prange and Margulies, 2002 [9] |
| 3.50, 6.84 | 319, 137 | Valardi et. al., 2005 [10] |
The complexity of the brain has given way to two approaches to researching this topic. The first approach forms models with complexities such as anisotropy and hyper-viscoelasticity, as it is known that these are fundamental aspects of brain behavior (Chatelin et al., 2012) [2]. The second approach models the material composition simply, including only essential components (i.e. density, elasticity, viscoelasticity), so as not to use incorrect parameters for complexities that may dramatically affect results. This approach assumes that if incorrect parameters are used for anisotropy and hyperelasticity, then the results will be less accurate than using a simple model with fewer unknown parameters. Rashid et al., 2012 [3] and many reports like it use the first approach and assume that a hyper-viscoelastic model is necessary in order to produce valid results under certain loads. Other reports have assumed that the added complexities of hyperelasticity or anisotropy are trivial for different circumstances (e.g. Brands et al., 2004) [4]. Either decision can produce meaningful results if the effect of the material assumptions is known and weighed with the conclusions. The following computational studies explores the role of hyperelasticity in the mechanics of the brain under rotational motion so that the effects of material assumptions in brain models are known.
Methods
Two computational studies were conducted using the finite element analysis software package Abaqus 2019 on a circular cross section of a virtual brain. The first study validated the accuracy of the results from a 0.6 mm mesh model by comparison to the results from a 0.2 mm mesh model. The second study provided a comparison between viscoelastic and hyper-viscoelastic behavior using damage criterion. For both studies, rotational loads were applied to the brain for each material composition and the shear strain response was analyzed.
Geometry.
A circular cross section of the brain and skull, modeled with Abaqus, was used for all tests and is shown below in Figure 1. The plane strain assumption was used.
Shown above is the cross section of the Abaqus model brain that was used for each test. The skull is shown in red and the brain is in green. The skull is defined as a rigid body and the brain material definition varies between viscoelastic or visco-hyperelastic throughout the studies.
Loading Specifications.
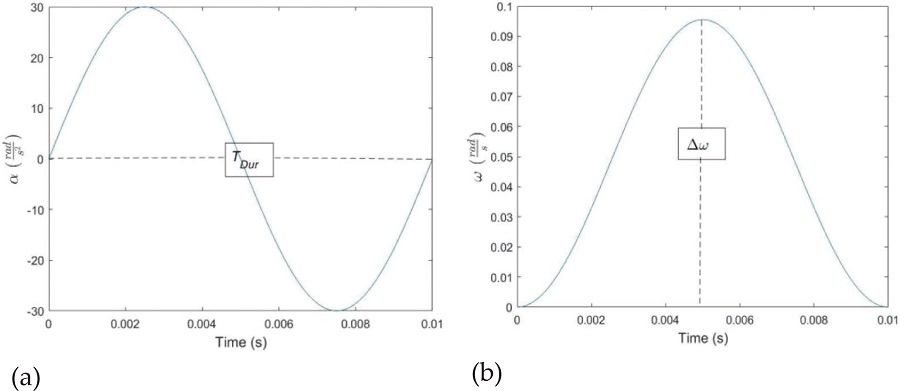
For each test, the system was subjected to a load defined by a sinusoidal rotational acceleration about the centroid of the brain. The parameters used to vary the input are TDur and Δω as shown below in Figure 2.
Ogden’s Hyperelastic Model.
For the computational studies performed in this report, a first order Ogden model, N=1 was used. The strain energy density equation for Ogden’s model of hyperelasticity is shown below in equation (1) [5].
(1)
The inputs to this model are the relaxed shear modulus, μ1, the alpha constant, α, and the D1 value, which is determined by the bulk modulus, k0 through the relation. Abaqus computes and outputs the total volume change, , and stretch values, λi, for each finite element of the model.
Mesh Validation
To ensure that appropriate mesh properties were used for the material comparison, four tests with and varying values of TDur = 0.2, 0.3, 0.5, and 1 ms were conducted for both a 0.6 mm and 0.2 mm brain mesh. The maximum shear strain, γ, was observed at a consistent point in time over a consistent area of the brain for each test. This area is shown in Figure 3 and the material parameters describing the brain are given in Table 2. The viscoelastic component is expressed in the time domain and the hyperelastic component is defined by the Ogden model. The results of the mesh comparison are compiled in Table 3 and reveal the extent to which a 0.6 mm mesh can produce reliable results. A 0.6 mm mesh is preferable to a 0.2 mm mesh as computation can be completed much faster.
The material parameters of the model used for the mesh comparison are shown below. The density used for both compositions is.
| Viscoelastic | Hyperelastic | ||||
|---|---|---|---|---|---|
| τi | μ1 | α | D1 | ||
| 0.84 | 0 | 0.1 | 1000 | −5 | 2*108 |
Tabulated below are the findings of the mesh comparison. Percent error was calculated under the assumption that the 0.2 mm mesh is accurate. The results from a 0.6 mm mesh become unreliable with pulse durations less than 2 ms.
| 2 ms Pulse | 3 ms Pulse | 5 ms Pulse | 10 ms Pulse | |
|---|---|---|---|---|
| γ max, 0.2 mm mesh | 0.394*10–3 | 0.587*10–3 | 0.963*10–3 | 1.878*10–3 |
| γ max, 0.2 mm mesh | 0.225*10–3 | 0.584*10–3 | 0.962*10–3 | 1.874*10–3 |
| Percent Error | 42.9 % | 0.511 % | 0.104% | 0.2130% |
The findings in Table 3 were used to determine which values of the loading specification, TDur, produce results that experience insignificant numerical dispersion. Only TDur values of 3 ms or higher can be relied on to produce accurate results when using a 0.6 mm mesh. Such a condition was used for the remainder of the tests.
Material Comparison Setup
This study compared the behavior of a viscoelastic model with that of a hyperviscoelastic model. Each test was evaluated against a maximum shear strain injury threshold to reveal differences between the models. A preliminary phase of these tests was completed to show which loading inputs would cause significant deformation of the brain. Once these potentially harmful inputs were known, another phase was completed with more tests using such inputs.
Material Parameters and Loading Inputs.
For every set of tests, 9 values of Δω and 13 values of TDur were combined, resulting in 117 tests with various loading inputs. Four sets of tests were completed, with each set using a consistent material composition. Lower and upper bounds of the relaxed shear modulus were used in order to understand if this value significantly contributes to differences in shear strain. For each bound of hyper-viscoelasticity, a corresponding composition of viscoelasticity was tested. The values for the corresponding compositions were obtained using Lamé parameter relations as explained below and shown in Table 4. This value was held constant for the lower and upper bounds. The relaxed shear modulus, μ1, was given a value of 1 kPa for the lower bound and 3 kPa for the upper bound. From these values of μ1 and K, the corresponding values of the Poisson’s ratio, ν, and Young’s modulus, E, were calculated using Lamé parameter relations [6].
The parameters for each material component are shown below. The viscoelastic component is in the time domain and the hyperelastic component is defined by the Ogden model. The units for each parameter are shown in brackets. The carrots indicate the same value was used for the lower bound as for the upper bound. The density used for all tests is.
| Viscoelasticity | Visco-Hyperelasticity | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| τi | ν | E | τi | μ1 | α | D1 | |||||
| Upper Bound | 0.84 | 0 | 0.1 | 0.499997 | 2999.99 | 0.84 | 0 | 0.1 | 1000 | −5 | 2*108 |
| Lower Bound | ^^ | ^^ | ^^ | 0.4999925 | 8999.95 | ^^ | ^^ | ^^ | 3000 | ^^ | ^^ |
The Injury Threshold.
In Morrison et. al., 2003 [7], it was suggested that brain cells will experience significant damage if their strain exceeds 10%. For the preliminary phase of tests, the 10% shear strain threshold was used. For the second phase of tests, two shear strain thresholds were used. A lower threshold of was used 5% along with the standard threshold of 10% to reveal whether the effects of the composition differences are exaggerated at higher strains.
Results
Maximum Acceleration Calculations
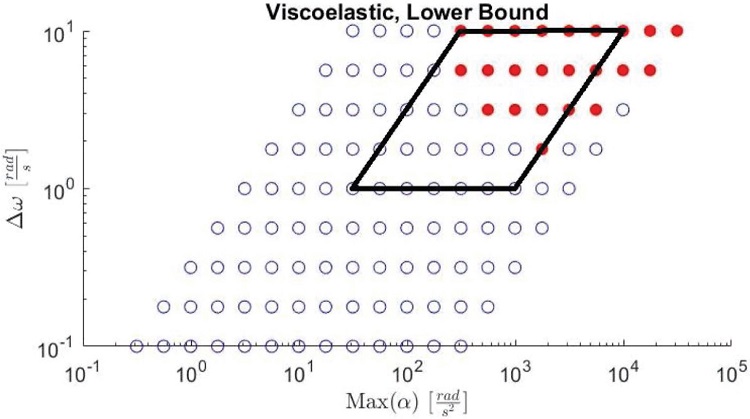
In order to represent the sets of tests, the maximum angular acceleration, Max(α), has been plotted against Δω. The value Max(a) for each test is derived from values for Δω and TDur. Shown in Figure 4 is the lower bound of the viscoelastic set of tests from the preliminary phase. On the x-axis of each plot is a logarithmic scale of the maximum angular acceleration, Max(α), of the skull. On the y-axis is the change in angular velocity, Δω, of the skull. Each point represents a test. Data points shown in red reveal tests where any element on the brain has exceeded the injury threshold.
The results from Figure 4 led to the second phase of tests using loading inputs that were finely incremented within the injury inducing inputs.
Shown above is the lower bound of the viscoelastic set of tests from the preliminary phase. The black lines show the loading input boundaries for which the second phase of tests are conducted. Notice that the two columns on the right side are excluded due to numerical dispersion, a concept that is explained in the Discussion section.
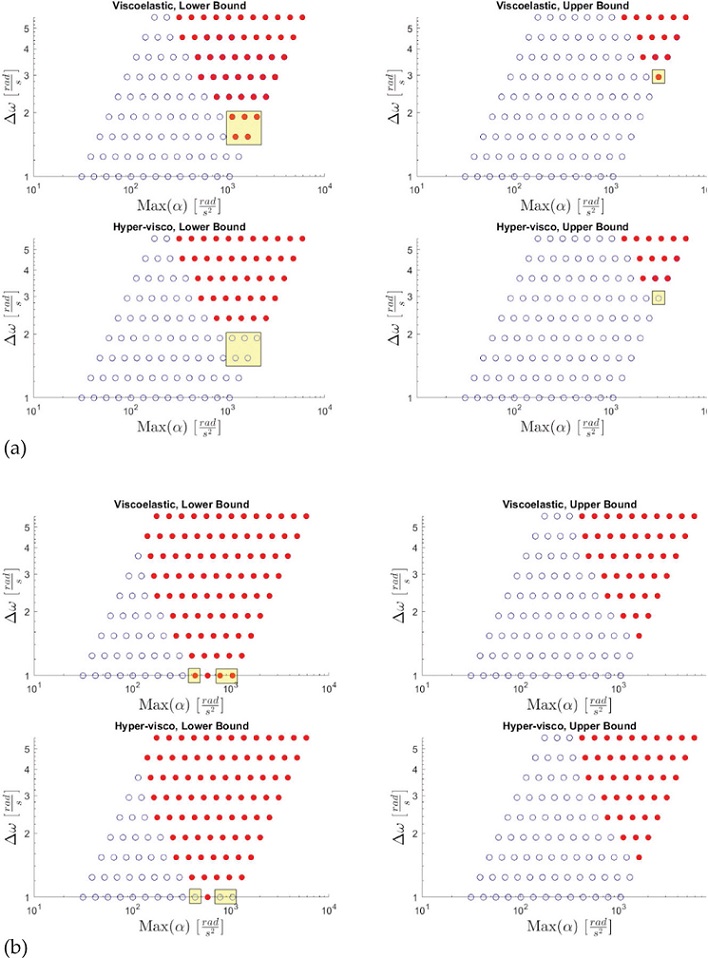
Material Comparison Results
The results of the second phase of tests are compiled in Figure 5 on page 10. The figure uses two different shear strain injury thresholds. Any differences between the visco-hyperelastic and viscoelastic compositions are highlighted in yellow. Three observations can be noted. The first is that a large acceleration is necessary to observe differences between the hyper-viscoelastic and viscoelastic models. Even when the change in angular velocity is high, no differences were observed between the viscoelastic and hyper-viscoelastic models unless significant acceleration was applied. Secondly, the differences caused by the hyperelastic component are more pronounced at higher strains. This is evidenced in that Figure 5a reveals more differences in shear strain behavior than Figure 5b. Lastly, the upper bound, with relaxed shear modulus μ1 = 3 kPa, has revealed only one difference at an angular acceleration. This indicates that the value of the shear modulus significantly contributes to the effect of hyperelasticity.
Discussion
Mesh Consideration.
The findings of the mesh comparison, compiled in Table 3, indicate that finite element analysis (FEA) requires a sufficiently fine mesh in order to produce reliable results. This is due to a phenomenon called numerical dispersion. Numerical dispersion occurs in tests when the simulated material exhibits a higher dispersivity than the true material [8]. For the case of modeling the brain, this means that deformation measures, such as strain, which are observed from the model will have a lower magnitude than what would be experienced by a real brain. Because the brain is especially compliant, it will be important for all researchers to check that numerical dispersion does not occur within their FEA models of the brain.
Shown above are the results of the tests given an injury condition of (a) 0.1 maximum shear strain and (b) 0.05 max shear strain. Data points in red reveal tests that recorded a maximum shear strain in the brain larger than the threshold. The differences between the viscoelastic and hyper-viscoelastic tests are highlighted in yellow.
Hyperelastic Effect Dependent on Shear Modulus.
Figure 5 on page 10 reveals that the shear modulus plays an important role in determining how hyperelasticity will affect the resultant shear strains. For the upper bound of the relaxed shear modulus, where μ1 = 3 kPa, only 1 of 16 tests that profile the injury threshold yielded a different result for the two models. This is held in contrast to the lower bound. For this bound, where μ1 = 1 kPa, 8 of 25 tests that profile the injury threshold yielded different results for the two models. All 9 of the tests that revealed differences between models consistently showed that the hyperelastic model was more resistant to shear deformation than the viscoelastic model.
Shown above are two stress-stretch curves of hyperelastic Ogden models in uniaxial tension with corresponding linear elastic stress-stretch curves. As the stretch is increased, the hyperelastic curves demand higher stresses than the linear elastic curves. Also note that as α is increased, this phenomenon is exaggerated.
Evenly spaced values of TDur and Δω were selected on a logarithmic scale from the intervals below.
| TDur[s] | |
|---|---|
Differences are Revealed at Extreme Loading Inputs.
When μ1 = 1 kPa, the hyperelastic component significantly contributes to the shear strain behavior for loading parameters and. This shows that quick rotations with high accelerations are where the effects of hyperelasticity are significant.
Hyperelastic Effect Dependent on Shear Strain Threshold.
As described in the Methods section on page 7, Figure 5a uses an injury threshold of γ > 0.10, as this has been considered the shear strain above which concussion is likely. Figure 5b uses a threshold of γ > 0.05 to study trends of the composition differences with higher strains. Figure 5 shows that the differences become exaggerated between the models as the threshold is increased. This result makes sense when considering the stress-stretch curve of a hyperelastic material. Figure 6 below provides an example of a comparison between a hyperelastic and purely elastic stress-stretch curve, where stretch is defined as. As is shown, the hyperelastic material requires greater stress in order to affect large strains. This attribute of hyperelastic materials helps to explain the resiliency of the models including the hyperelastic component.
Implications for Future Work.
If a simple viscoelastic model is being used, then there will be less resistance to large shear strains. This means that if there are observable differences between the model and actuality, it would be that the brain experiences less shear strain than the model predicts. If, on the other hand, a hyper-viscoelastic model is being used, then any differences between the model and actuality would show that the model is more resistant to high shear strains than the true brain. This knowledge lets researchers with simple linear viscoelastic models know that their models tend to overestimate shear strain at extreme loading conditions. Furthermore, hyperelastic models with high shear moduli and large α values are more resistant to shear strain, meaning that the model tends to underpredict shear strain at extreme loading conditions. This is cause for warning as an underprediction in shear strain can lead to flaws in safety mechanism designs that allow for large shear strains to propagate in the brain, which are known to cause injury.
Conclusions
The following conclusions can be drawn from this research.
The hyperelastic tendency is to reduce the maximum strain caused by rotational loads.
The differences between viscoelastic and hyper-viscoelastic models increase as larger shear strains are affected on the brain.
The relaxed shear modulus value contributes to the effect of hyperelasticity on shear strain.
It is at the extreme loading conditions where differences in models become significant. Significant differences between a viscoelastic and hyper-viscoelastic model are observed for tests when the angular acceleration and the relaxed shear modulus of the brain is μ1 < 1 kPa. If a relaxed shear modulus of μ1 > 3 kPa is being used, the effect of hyperelasticity on shear strain is only observed for loads with angular accelerations.
It is crucial for all researchers to ensure that numerical dispersion does not occur within FEA models of the brain.
References
1. Miller, K., Chinzei, K., Mechanical properties of brain tissue in tension, Journal of Biomechanics 35, 483–490, 2002.
2. Chatelin, S., Deck, C., Willinger, An anisotropic viscous hyperelastic constitutive law for brain material finite element modeling, Biorheology, 2012.
3. Rashid, B., Destrade, M, Gilchrist, M. D., HYPERELASTIC AND VISCOELASTIC PROPERTIES OF BRAIN TISSUE IN TENSION, IMECE2012, 2012.
4. Brands, D.W.A., Peters, G.W.M., Bovendeerd, P.H.M., Design and numerical implementation of a 3-D non-linear viscoelastic constitutive model for brain tissue during impact, Journal of Biomechanics 37, 127–134, 2004.
5. Gasser, T. C., Holzapfel, G. A., and Ogden, R. W., “Hyperelastic Modelling of Arterial Layers with Distributed Collagen Fibre Orientations,” Journal of the Royal Society Interface, vol. 3, pp. 15–35, 2006.
6. Carmen Chicone, Chapter 18 - Elasticity: Basic Theory and Equations of Motion, Editor(s): Carmen Chicone, An Invitation to Applied Mathematics, Academic Press, 2017, Pages 577–670, ISBN 9780128041536.
7. Morrison, B., Cater, H. L., Wang, C. C., Thomas, F. C., Hung, C. T., Ateshian, G. A., Sundstrom, L. E., A tissue level tolerance criterion for living brain developed with an In Vitro model of traumatic mechanical loading, Stapp Car Crash J., 47, 93–105.2003.
8. Trefethen, L. N., Numerical Linear Algebra, 191–205, 1994
9. Prange, M. T., Margulies, S. S., Regional, Directional, and Age-Dependent Properties of the Brain Undergoing Large Deformation, Journal of Biomechanical Engineering 124, 244–252, 2002
10. Velardi, F., Fraternali, F., Angelillo, M., Anisotropic constitutive equations and experimental tensile behavior of brain tissue, Springer-Verlag, 2005